4.1 Cryptographic Protocols
Up to this point, we have primarily considered encryption systems, that is, methods to encrypt and decrypt secret messages. Recall that cryptosystems can be classified as symmetric key or public (asymmetric) key. In the former, both the encoding and decoding algorithms are supposedly known only to the sender and receiver, while in the latter, the encryption method is public knowledge, but only the receiver knows how to decode.
Secure confidential message transmission is only one type of task that must be done with secrecy and there are many other tasks and procedures that are important in cryptography. What is meant by a cryptographic task will be made a bit more precise via specific examples below.
Suppose that several parties want to perform a cryptographic task. To accomplish this the involved parties must communicate and cooperate. Further each party has to obey certain rules and use certain preassigned algorithms. The set of all methods and algorithms used to perform such a cryptographic task is called a cryptographic protocol. A cryptosystem is just one type of cryptographic protocol. Formally:
Definition 4.1.1. Suppose that several parties want to manage a cryptographical task. Then they must communicate with each and cooperate, and hence, each party must follows certain rules and implement certain agreed upon algorithms. The set of all such methods and rules to perform a cryptographical task is called a cryptographic protocol.
Several cryptographic tasks are described below. Each will be discussed in more detail later in this chapter. As more techniques are introduced, we will look at further instances of these cryptographic tasks, and cryptographic protocols to handle them.
(1) Authentication: Authentication refers to the process of determining that a message, supposedly from a given person, does come from that person and further has not been tampered with. Included in the general topic of authentication are the concepts of hash functions and digital signatures. Hash functions will be introduced in the next section. Another important usage is password identification. We will discuss a secure backup password system using non-commutative methods later in the book.
(2) Key Exchange and Key Transport: In a key exchange protocol two people, usually called Bob and Alice, exchange a secret shared key to be used in some symmetric encryption. In a key transport protocol, one party transports to another, a secret key that is to be used.
(3) Secret Sharing: Secret sharing involves methods where some secret is to be shared by k people but not available to any proper subset of them. There are many ways to accomplish this and it is related to a classical lock and key problem. A beautiful simple solution to the general problem, using polynomial interpolation, is due by Shamir. In Section 4.4 we will describe Shamir’s technique as well as a nice geometric alternative to it.
(4) Zero Knowledge Proof: A zero-knowledge proof is an argument that convinces someone that you have solved a problem, for example a combinatorial problem, without giving away the solution. This is tied to authentication.
4.2 Cryptographic Hash Functions
Before describing individual cryptographic protocols, we introduce the concept of cryptographic hash functions. These functions play a crucial role in many different types of protocols.
Modern cryptography is done via a computer. Therefore all messages, both plaintext and ciphertext, can actually be presented as binary strings, that is strings of binary bits, {0,1}’s. We first define a hash function as a function on bit strings. Later we will give a more general definition.
Definition 4.2.1. A cryptographic hash function is a deterministic function
that returns for each arbitrary block of data, called a message, a fixed size bit string. The bit string returned for a given message is called its hash value. The function should have the property that a change in the data will change the hash value. The hash value is also called the digest.
To satisfy the properties necessary to be used in a cryptographic protocol an ideal hash function has the following properties:
(1) It is easy to compute the hash value for any given message.
(2) It is infeasible to find a message that has a given hash value. This is called pre image resistance.
(3) It is infeasible to modify a message without changing its hash.
(4) It is infeasible to find two different messages with the same hash value. This is called collision resistance.
Hash functions can be used with encryption functions to construct authenticated encryption protocols. Suppose that Bob and Alice want to communicate openly. They have exchanged a secret key k that supposedly only they know. Let fk be an encryption function or encryption algorithm based on the key k. Alice wants to send the message m to Bob and m is given as a binary bit string. Alice sends to Bob
where ® is the XOR operation, that is, addition modulo 2.
Bob knows the key k and hence its hash value h(k). He now computes
Since addition modulo 2 has order 2 we have
Bob now applies the decryption algorithm gk to decode the message.
Alice could have just as easily sent fK(m) ® k. However, sending the hash has two benefits. Usually the hash is shorter than the key and from the properties of hash functions it gives another level of security. Used in this manner, a cryptographic hash function can serve as a digital signature. As we will see, tying the secret key to the actual encryption in this manner is the basis for the ElGamal and Elliptic curve cryptographic methods.
The encryption algorithm fk is usually a symmetric key encryption so that anyone knowing k can encrypt and decrypt easily. However, it should be resistant to plaintext- ciphertext attacks. That is, if an attacker gains some knowledge of a piece of plaintext together with the corresponding ciphertext, it should not compromise the whole system.
The encryption algorithm can either be a block cipher or a stream cipher.
For the following, especially the examples, we give a more general definition.
Definition 4.2.2. Let M1, M2 be non empty sets. Then a (cryptographic) hash function is a map f : M1 → M2 with the following properties:
(1) f is free of collisions, that is, there is no efficient method to find two elements ,x1; x2 ∈ M1 with f (x1) = f (x2).
(2) f is not efficiently invertible, that is, if y ∈ Im(f) then there is no efficient way to find x ∈ M1 with f (x) = y.
Although an ideal hash function is not efficiently invertible, to be useful in a cryptographic situation there must be a way to invert such a function or at least partially invert it on the set of messages. This leads us to the concept of a trapdoor.
Definition 4.2.3. A hash function with a trapdoor is a map f : M1 — M2 satisfying:
(1) f is free of collisions.
(2) There is a secret key by means of which f is efficiently invertible.
(3) If one does not know the secret key then f is not efficiently invertible.
The secret key is the trapdoor.
Some Examples of Hash Functions
Here we present several examples of hash functions.
(1) Quadratic Residues as Hash Functions: Recall that if n is an integer and x2 = b (mod n) then b is called a quadratic residue. Hence b is a quadratic residue modulo n if 
has a squareroot in 
n. If not it is a quadratic non-residue. We will discuss quadratic residues in Chapter 4.
Let p, q be two distinct odd primes and let n = pq. Determine one quadratic nonresidue y modulo n with y ∈ {1,…,n - 1} and the greatest common divisor
(y, n) = 1. Now consider the function
with N ≥ 1 and 
(mod n).
Then the following hold:
(a) If ε = 0 then yεm2 is a quadratic residue modulo n.
(b) If ε = 1 then yεm2 is a quadratic non-residue modulo n.
(c) The function f is collision free in the first argument. That is, we always have 
(d) If we choose N in such a way that the quadratic residues m2 modulo n for m = 0,1,…, N are pairwise distinct then f is free of collisions.
There is no known efficient method to discover whether or not y is a quadratic residue modulo n = pq if p and q are unknown. Therefore the function f is a hash function.
(2) Modular Squaring as a Hash Function: Let p, q ≥ 3 be two distinct odd primes and let n = pq. Let 
be the unit group modulo n (see Chapter 5 for more details). Now consider the function
Then the following hold:
(a) If y ∈ im(f) then |f-1(y)| = 4 (see Chapter 5, Section 5.2).
(b) If we know p and q then for y ∈ im(f) we may find efficiently one x such that y = x2 = f (x).
(c) If we only know n but not p and q there is no efficient algorithm to find an x such that x2 = y for y ∈ im(f). All the known algorithms are of exponential order (see Chapter 3).
(d) If we restrict f to the set
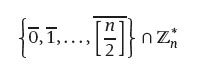
then f is free of collisions and may be used as a hash function with a trapdoor, the secret keys being p and q.
(3) Discrete Logarithm as Hash Functions: Recall that if 
is a cyclic group and h ∈ G with h = gt then t is called a discrete logarithm of h. If p is a prime then 
is a cyclic group.
Let p be a large odd prime and g a primitive root modulo p, that is g is a generator of the unit group . Now consider the function
There is no known efficient algorithm to solve the discrete log problem if p - 1 has a large prime factor. Hence in this case f is a hash function with the generator g as the trapdoor.
(4) Factorization as a Hash Function: Let P denote the set of all odd prime numbers. Define the function
given by
There is no known efficient algorithm to factorize n = pq if both p - 1 and q - 1 have large prime factors. Hence in this case the function f is a hash function with a trapdoor.
We note that each of these, especially (3) and (4), can be made the basis of a public key exchange protocol. We will return to these in Chapter 6 when we introduce the Diffie-Hellman and RSA protocols.
4.3 Authentication Protocols
When a confidential message is transmitted there are several important aspects that must be verified. First, there must be a verification to the receiver that the sender is who he or she claims to be. Secondly, there must be a verification to the sender that the receiver is also who he or she claims to be. Next, there should be a verification that the message has not been altered in any way. Finally, there should be in many message transmissions, some form of undeniability, that is a procedure that makes it impossible for a sender to claim that he or she did not send the message. All of these verifications are handled by an authentication protocol.
There are many specialized types of authentication protocols handling one or more of the verification tasks mentioned in the above paragraph. Here we will discuss just the general ideas in message authentication.
Hash functions provide one technique for message authentication. This was explained briefly in the previous section. Suppose that m is the true message and h is a hash function. What is done in this type of authentication protocol is to verify, using a public key system, h(m) the hash value of the message. From the collision and preimage resistance properties of a hash function, verification of the hash value of the message provides verification of the message itself. Similarly, included with the message could be the hash value of the sender. Again because of the properties of the hash function this provides authentication of the sender.
Any public key encryption system has a type of built-in verification. This will be explained here and explained again in Chapter 7 on public key methods. In that chapter we will also see how to take a specific public key encryption system and build from it an authentication procedure. In Chapter 7 we will introduce how to accomplish this with the RSA encryption system and in Chapter 8 how to do authentication via elliptic curves.
As introduced in Chapter 1, the basic idea in a public key cryptosystem is to have a one-way function or trapdoor function. That is a function which is easy to implement but very hard to invert. Hence it becomes simple to encrypt a message but very hard, unless you know the inverse, to decrypt. The trapdoor is the simple knowledge that one needs to invert.
The standard model for public key systems is the following. We suppose that Alice’s public key is an injective function fA and her private key is gA, the left inverse of fA. It follows that for any message m we have gA(fA(m)) = m. Here the function fA indexed for A is Alice’s public key. Similarly Bob has a public key fB.
Alice wants to send a message to Bob. The encrypting map fA for Alice is public knowledge as well as the encrypting map fB for Bob. On the other hand, the decryption algorithms gA and gB are secret and known only to Alice and Bob respectively. Let m be the message Alice wants to send to Bob. She sends fB(m).The function fB is public knowledge and it is easy to encrypt. To decrypt Bob now applies gB to what he has received. Recall that presumably only he knows his private key gB. Doing this he obtains
and hence recovers the message.
If Bob receives a message, how can he be certain that it actually comes from Alice. Within this standard model it is relatively easy to build in verification or authentication. As above let m be the message Alice wants to send to Bob. Now instead of sending fB(m) she sends
Now to decode Bob applies first gB, which is his private key so that only he knows. This gives him
He then looks up fA which is publically available and applies this
to obtain the message. This supplies verification and authentication in the following manner. Suppose P is Alice’s verification; signature, social security number etc. If Bob receives fB(P) it could be sent by anyone since fB is public. On the other hand, since only Alice supposedly knows gA getting a reasonable message from fA(gB(fB(gA(m)))) would verify that it is from Alice. Applying gB alone should result in nonsense.
Important in all authentication protocols is the concept of a message authentication code or MAC. This is also called a tag. A MAC is a short piece of information used to authenticate a message. In using a hash function for authentication the hash value is the tag.
In a MAC protocol, a secret key and an arbitrary length message m to be authenticated, are taken as input. Then a MAC value or tag is outputted. The MAC value protects both the message data integrity as well as its authenticity by allowing verifier’s to detect any changes in the message content. A MAC is stronger than just using a hash value.
It is assumed that both sender and receiver have the message m to be verified. The sender generates a secret key k then computes, as a function of both the key and the message, a MAC x. The sender then transmits the secret key and the MAC to the receiver. The receiver then computes in the same manner as a function of the message and the transmitted secret key the MAC value. If the same MAC x is found by the receiver then the message is authenticated and the integrity checked. If they differ something is not right.
4.4 Digital Signatures
A strong form of authentication is given by a digital signature protocol. This is to be thought of as the analog of a written signature but for electronic or digital messages. A digital signature is then a mathematical procedure to handle the following authentication needs;
(1) verifying the authenticity of the sender,
(2) verifying that the message has not been tampered with,
(3) providing a means to prevent deniability.
These are the essential requirements of any signature, written or electronic. A digital signature is then tied to a given electronically transmitted message.
In many countries, including the United States and the European Union, digital signatures carry the same legal weight as handwritten signatures.
Mathematically, a digital signature protocol consists of three cryptographic algorithms: a key generation algorithm, a digital signing algorithm and a digital signature verification algorithm. In more detail:
(1) A Key Generation Algorithm is an algorithm that selects a private key randomly from a set of private keys and then outputs the private key and a corresponding public key.
(2) A Digital Signing Algorithm is an algorithm that given a transmitted message m produces a signature that will be tied to the message.
(3) A Digital Signature Verification Algorithm is an algorithm that accepts three inputs, a message m, a public key k and a signature S and then based on these inputs either accepts or rejects the authenticity of the message.
It is assumed that the authenticity of the given signature for a fixed message and a fixed private key is verified by using the corresponding public key given in the key generation algorithm. It is also required that it is computationally infeasible to generate a valid digital signature for anyone not possessing the private key.
In most applications, the hash value of the message is what is signed rather then the message itself. This is basically for efficiency purposes. Signing algorithms are public key and hence relatively time inefficient. Using the hash value speeds up the process. Further the message often has to be broken up into smaller pieces to be transmitted. If each piece is to be signed there is no verification that all the constituent blocks are included or in the proper order. Signing the hash value of the whole message serves as an authentication of the whole message.
Any public key message transmission system can be used to develop a digital signature protocol. In this section we describe the Digital Signature Algorithm or DSA which has become the signing standard in many countries where digital signatures are legally binding. This is based on the ElGamal Signature Method. Other digital signing protocols, such as the RSA signature method, will be described in later chapters.
In the Digital Signature Algorithm a signed message is to be sent from party A to party B. The first step is to choose the parameters and then the per-user keys, both public and private. These steps are followed by the signing algorithm and finally the verification algorithm. There is some basic number theory involved in the DSA, and a reader, if desired, may come back and look at this example after reading Chapter 5 on basic number theoretic methods. In the description of DSA below *p represents the non-zero elements of the modular ring p. Recall (or see Chapter 5) that if p is a prime then each non-zero element x ∈p has an inverse, that is an element y such that xy is congruent to 1 modulo p.
DSA: Choice of Parameters and Setup
(1) A chooses a large odd prime integer q.
(2) A chooses a second prime integer p with p = 1 (mod q). Such primes p exist (see [FR]).
(3) |*p| = p - 1an q | (p - 1). Then there exists an integer g such that 
has order q in *p (see Chapter 5). To calculate such a g we do as follow:
(i) Choose a random integer g0 ∈ {1,…,p - 1} and calculate 
modulo p.
(ii) Repeat (i) as long as the result is not congruent to 1 modulo p. Then define . The order of g is q because q is prime.
DSA: Signature Private and Public Keys
(1) A chooses as a private key a random x ∈{1,…, p - 1}.
(2) A calculates y = gx (mod p).
(3) The public key for the signing algorithm is (p, q, g, y) while the private key is x.
DSA: Signing Algorithm
(1) Let m be the transmitted message and h(m) its hash value for a given hash function h.
(2) A generates randomly per message an integer k ∈ {1,…, q - 1} and calculates
r = (gk (mod p)) (mod q).
(3) If r = 0 choose another k.
(4) Calculate s = k-1(h(m) + xr) (mod q).
(5) If s = 0 choose another k.
(6) The signature is (r, s).
DSA: Verification Algorithm
(1) B calculates an integer t with st ≡ 1 (mod(p - 1)) and then the two integers
(2) B then determines the integer
and applies the division algorithm with division by q. If the remainder is equal to r then B accepts the signature.
This algorithm is correct, that is the verification algorithm will always accept a genuine signature. From gq = 1 (modp) we get
and this gives the remainder r modulo q.
As with hand-written signatures there must be security against forgery. For digital signatures there are various different levels of forgeries.
(1) A total break is where an attacker recovers the signing key.
(2) A universal forgery is where an attacker gains the ability to forge signatures for any message.
(3) A selective forgery is where an attacker gains the ability to forge a signature on a message of the attacker’s choice.
(4) An existential forgery is where an attacker recovers a valid message-signature pair not already known to the attacker.
Whereas an ideal digital signature protocol withstands all types of forgeries, a good secure digital signature protocol must be able at least to withstand an existential forgery. In their seminal paper [GMR] Goldwasser, Micali and Rivest describe a hierarchy of possible attacks against digital signature protocols. These mirror the types of attacks on general cryptographic protocols.
(1) A key-only attack is where an attacker has access to only the public verification key.
(2) A known message attack is where an attacker has access to valid signatures for a variety of messages known but not chosen by the attacker.
(3) An adaptive chosen message attack is where an attacker has access to signatures on arbitrary chosen messages.
Closely related to digital signatures is the problem of secure password verification and the preparation of a challenge response system. We describe these in more detail in Section 10.7 in connection with a group based method for challenge response password verification.
4.5 Secret Sharing Schemes
A secret sharing scheme is a method to distribute a secret among a group of participants by giving a share of the secret to each. The secret can be recovered only if a sufficient number of participants combine their shares.
Formally we have the following secret sharing problem. We have a secret K and a group of n participants. This group is called the access control group. A dealer allocates shares to each participant under given conditions. If a sufficient number of participants combine their shares then the secret can be recovered. If t ≤ n then an (t, n)-threshold scheme is one with n total participants and in which any t participants can combine their shares and recover the secret but not fewer than t. The number t is called the threshold. It is a secure secret sharing scheme if given less than the threshold there is no chance to recover the secret. If a measure is placed on the set of secrets, and on the set of shares, security can be made precise by saying that given less than the threshold all secrets are equally likely but given the threshold there is a unique secret. Secret sharing is an old idea but was formalized mathematically in independent papers in 1979 by Adi Shamir [Shal] and George Blakely [Bla].
In the 1979 paper Shamir [Shal] proposed a beautiful (t, n)-threshold scheme, based on polynomial interpolation, that has many desirable properties. It has become the standard method for solving the (t, n)-secret sharing problem, although there are modifications for different situations that we will discuss in this section. Blakely in his original paper [Bla] proposed a geometric solution based on hyperplanes that is less space efficient, for computer storage, than Shamir’s. In Blakely’s scheme the distributed shares are larger than the secret, whereas in Shamir’s scheme they are the same size.
The protection of a private key in an encryption protocol provides strong motivation for the ideas of secret sharing. In an encryption protocol, only the private key used in the encryption scheme is the secret, and not the encryption method itself. When we examined the problem of maintaining sensitive information, we considered two issues: availability and secrecy. If only one person keeps the entire secret, then there is ariskthatthe person mightlose thesecretorthe person mightnot be availablewhen the secret is needed. Hence it is often wise to allow several people to have access to the secret. On the other hand, the more people who can access the secret, the higher the chance the secret will be leaked. A secret sharing scheme is designed to solve these issues by splitting a secret into multiple shares and distributing these shares among a group of participants. The secret can only be recovered when the participants of an authorized subset join together to combine their shares.
A secret sharing scheme is a cryptographic primitive with many applications, such as in security protocols, multiparty computation (MPC), Pretty Good Privacy (PGP) key recovering, visual cryptography, threshold cryptography, threshold signature, etc. The paper by Chum, Fine and Zhang [CFZ] provides a strong description of general secret sharing and access security methods.
4.5.1 The Shamir Secret Sharing Scheme
Given a secret K, a (t, n)-secret sharing threshold scheme is a cryptographic primitive in which a secret is split into pieces (shares) and distributed among a collection of n participants {px,p2,… ,pn} so that any group of t or more participants, with (t ≤ n), can recover the secret. Meanwhile, any group of t - 1 or fewer participants cannot recover the secret. By sharing a secret in this way the availability and reliability issues can be solved.
Shamir solved the secret sharing problem in a very simple but beautiful manner using polynomial interpolation. The general idea in a Shamir (t, n)-threshold scheme is the following. Let F be any field and (x1 y1,…, (xn, yn) be n points in F2 with pairwise distinct xi. A polynomial P(x) over F interpolates these points if P(x;) = yi for i = 1,…, n. The polynomial P(x) is called an interpolating polynomial for the given points. The crucial theoretical result is that for any n points (xi, yi) with distinct xi there always exists a unique interpolating polynomial of degree ≤ n - 1.
Theorem 4.5.1 (Polynomial Interpolation Theorem). Let F be any field and xx,…, xn be n pairwise distinct elements of F and yx,…, yn any elements of F. Then there exists a unique polynomial of degree ≤ n - 1 that interpolates the n points (xi, yi), i = 1,…, n.
Using this theorem, the Shamir (t, n)-threshold scheme works in the following manner. A field F with more than n elements is chosen. In general if F is a finite field we assume that the order of F is much much larger than n, the number of participants. The secret K is taken as an element of the field F and a polynomial P(x) of degree t - 1 is chosen with the secret K as its constant term. Then pairwise distinct elements of F, x1,…,xn, are chosen with no xi = 0. The points (xi,P(xi)) are distributed to each of the n participants. By the polynomial interpolation theorem, Theorem 4.6.1, any t participants can determine the interpolating polynomial P(x) and hence recover the secret K. Given an infinite field and less than t people there are infinitely many polynomials of degree t - 1 that can interpolate the given points and hence finding the correct polynomial has probability zero. In a finite field Shamir proved that under random choices for the xi each secret in F is equally likely so guessing the secret is a random choice from F.
In the next subsection an alternative version to this Shamir scheme will be outlined that uses inner product spaces and the closest vector theorem rather than interpolation.
We now present a more explicit version of the Shamir scheme using the finite field F = GF(q) where q = pk with k > 1 andp is a large prime. By using a finite field Shamir was able to place a finite measure on the set of plaintexts and ciphertexts and showed that with this scheme if there are less than t people all secrets are equally likely.
In a secret sharing protocol we assume that there is a dealer who fairly and correctly distributes the shares among the participants.
The Shamir (t, n)-Threshold Secret Sharing Scheme
Share distribution: Let K be the secret. The dealer generates a polynomial P(x) of degree at most t - 1 over F = GF(q), where q is much larger than n as follows:
where a0 = K is the secret, a1…, at-1 ∈ F and are generated randomly.
The dealer arbitrarily chooses pairwise distinct xi ∈ F{0}, i = 1,2,…, n.Usually, xi = i will be chosen for simplicity. xx, x2,…,xn are stored in a public area. The dealer calculates y = P(xi), i = 1,2,…, n, and distributes to the n participants via a secure channel so that each participant Pi gets one share yi. For the rest of the paper, we will not repeat the criteria of the generation of the coefficient ai of the polynomial P(x) and the calculation of the shares P(xi).
Secret Recovery (i): When any t participants join together, we have the following system of t equations. For simplicity, we assume the participants p1, p2, …,pt join together.
In matrix representation, it will be:
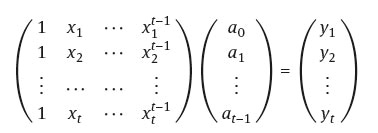
Let M be the above t x t Vandermonde matrix. Its determinant is
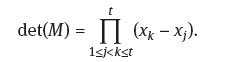
Since we choose pairwise different points for the participants, that is, pairwise distinct x,’s, det(M) ≠ 0, and this guarantees a unique solution. We can solve the system of equations by Gaussian elimination or Cramer’s rule. Hence the secret can be recovered.
Secret Recovery (ii): Another method is to use Lagrange interpolation. We can construct the polynomial of degree at most t - 1by any t different points (x1 yx),…, (xt, yt) as
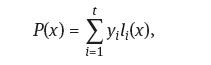
where
So, the secret a0 will be
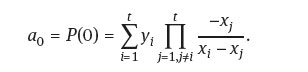
Shamir in his original paper was able to prove that this secret sharing scheme is perfect in the sense that for t - 1 participants any secret K ∈ F is equally likely. If F is an infinite field, then the probability of correctly guessing the secret is zero.
4.5.2 Alternatives for Secret Sharing Protocols
In this section and the next we describe some alternatives and enhancements to the Shamir Secret Sharing Scheme. The first alternative is a geometric method based on the closest vector theorem and introduced in [CFRZ]. It is similar to the original Blakely scheme but has the advantage that the secret is the same size as the shares. This was not the case in the Blakely protocol. This scheme, like the Shamir scheme, is also perfect in the sense that any t people out of the size n access control group can recover the secret but given less than t each possible secret is equally likely.
The Shamir scheme depends on the uniqueness of interpolating polynomials. The geometric alternative scheme depends on the closest vector theorem.
Recall the following facts. Let W be a real inner product space and V a subspace of finite dimension t. Suppose that w ∈ W and e1, e2,…,et is an orthonormal basis of V. Then the closest vector theorem is the following (see [Atk]).
Theorem 4.5.2 (Closest Vector Theorem). Let W be areal inner product space and V a subspace of finite dimension t. Suppose that w ∈ W, with w not in V, and e1, e2,…,etis an orthonormal basis of V. Then the unique vector w* ∈ V closest to w is given by
where < , > is the inner product on W.
Notice that given any basis for the subspace V, the Gram-Schmidt orthonormalization procedure (see [Atk]) can be used to find an orthonormal basis for V. Hence given w ∈ W we can algorithmically always find w*, the unique vector in V closest to w. If a basis for V is not known and we only have knowledge or information on proper subspace spans in V of dimension less than t we cannot do this procedure and any point in W can be the secret. That is, if we do not have complete knowledge of a basis for V, we cannot apply the closest vector theorem. Further, since given a subspace of dimension less than t there are infinitely many subspaces of dimension t properly containing it, there is a probability of zero of obtaining the subspace V with only partial knowledge.
The Secret Sharing Scheme
We start with an inner product space W of dimension m and an access control group of size n. We assume that the dimension m of W is much greater than n, that is m » n. Within W there is a hidden subspace V of dimension t < n. The secret to be shared is given as an element in this hidden subspace, that is the secret v ∈ V a vector in V.
The dealer distributes to each of the n members of the access control group, i = 1,…, n, two vectors, vi, w, where vi ∈ V, and w is a vector in the big space W. The common vector w has the property that w £ V and v is the vector in V closest to w. In general the vector w can be given publically. The set {v1, v2,…, vn} has the property that any subset of size t is independent. Hence any subset of size t determines a basis for V.
Suppose t valid users get together. They can determine a basis for V and hence using the Gram-Schmidt procedure (see [Atk]) determine an orthonormal basis. Since w is given, they can determine v by the closest vector theorem and recover the secret.
Given a subset of size less than t the given vectors generate a subspace of V of dimension less than t and hence in W there are infinitely many extensions to subspaces of dimension t. This implies that determining V with less than t elements of a basis has probability zero.
As suggested by Shamir the secret should be altered periodically. In this method it is extremely easy to change the secret v without altering much of the scheme; simply send each user a new w.
This is a general method like the Shamir protocol. In [FMoR], Fine, Moldenhauer and Rosenberger, compared several different secret sharing plans including the classic Shamir plan and the CFRZ plan.
In many instances more involved secret sharing tasks must be handled. As an example consider the following situation. We are in a company that has a directors and vice-directors. The directors and vice-directors are in the access control group but they do not have equal weight. Suppose that a secret can be recovered only if one of the following conditions is satisfied:
(a) two directors of the company cooperate;
(b) three vice-directors of the company cooperate;
(c) one director and two vice-directors of the company cooperate.
Thus here the threshold for the access control group differs depending on the status of the members.
A geometric method to handle this more difficult cryptographic task can done as follows:
(1) Choose a sufficiently large finite field 
with p a prime, n ≥ 1, or take K = Q.
(2) Consider the 3-space K3 and choose the point (0,0, s) on the z-axis where s is the secret.
(3) Choose in K3 randomly a plane E which contains the point (0,0, s) but which does not contain the z-axis at all.
(4) Choose randomly in E a straight line G which intersects the z-axis at the point (0, 0, s).
(5) Choose randomly on G (0,0, s) pairwise distinct points D1,…,Dk which are distributed to the directors.
(6) Choose randomly on E G pairwise distinct points V1,…, Vt such that points of the Vi are on one straight line and that no point Dk is on a straight line through two distinct points Vi and Vj. The points V1,…, Vt are distributed to the vice-directors.
This protocol then satisfies the desired conditions for the access control groups.
(1) Any two of the directors can calculate G and hence (0,0, s).
(2) Any three of the vice-directors can calculate E and hence (0,0, s).
(3) Any one of the directors combined with any two of the vice-directors can calculate E and hence (0,0, s).
4.5.3 Verifying Secret Sharing Protocols (VSS)
In a standard secret sharing protocol it is assumed that the dealer and the participants are honest. To ensure the proper behavior of the dealer and the participants we enhance the standard secret sharing scheme. A verifying secret-sharing protocol, denoted VSS, is one such enhancement. The aim of a VSS protocol is to be certain that the dealer and the participants behave correctly. A verifiable secret sharing protocol ensures that even if the dealer is dishonest there is a well-defined secret that the participants can recover. Verifiable secret sharing is important in secure multiparty computation.
There are many different verifiable secret sharing protocols (see [CFZ]). We first consider the case of a (2,2)-VSS and then give a generalization. We must construct a protocol where we can be certain that the dealer and the participants behave correctly. This first VSS protocol uses finite group theory. For a formal definition of homomorphism and isomorphism see Chapter 9.
(1) Let G and H be two groups and 
: 
be a group homomorphism so that
which is also a hash function.
(2) Let s ∈ G be the secret. The dealer chooses g1, g2 ∈ G with g1g2 = s and publishes (g1), (g2). Nobody can efficiently calculate s from the published data since is a hash function. However, everyone can verify that (s) = (g1) (g2).
(3) The dealer tells g1 to the participant A1 and g2 to the participant A2. Each Ai can calculate (g) from his secret gi and can check if the correct partial secret was received.
(4) When the participants reconstruct the secret s each Ai can prove if the other participant has exposed his correct partial secret by calculating $ (g) and comparing with the published values.
We now consider a more general (t, n)-VSS protocol. This example requires some elementary number theory. The required material can be found in the next chapter and a reader may want to complete that and then return to this section. Recall that if p is a prime then an integer g is a primitive element modulo p if the order of g is p — 1in the multiplicative group . For an integer g we let denote its residue class modulo p.
In the situation from the (2,2)-VSS protocol above we choose for the group G the additive group modulo (p — 1), that is 
. For H we choose the multiplicative group (, ) where p is a sufficiently large prime.
Let g be a primitive element modulo p. As a hash function we choose
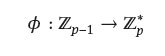
by
The dealer chooses randomly a polynomial
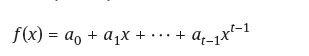
where 
and a0 = s is the secret.
The dealer then publishes 
. Recall that 
.
The dealer chooses randomly pairwise distinct elements 
. He calculates 
. He then publishes the values 
Then:
(a) Each participant Ai can prove if they received s; correctly by calculating and comparing with the published values.
(b) Each participant can prove if
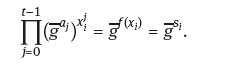
Practically the dealer cannot cheat. All distributions from the dealer can be proved by the participants.
Finally we present another protocol similar to the one above, due to ElGamal, where the participants cannot cheat but discrepancies from the dealer are hard to discover. This is known as the ElGamal (t, n)-threshold signature protocol.
(1) The participants reach an agreement on two large primes p, q with 
and a hash function 
. We assume that 
is the set of plain text units.
(2) There exists a unique cyclic subgroup Gq of with q elements (see the ElGamal signature method). The participants reach an agreement on a generator g ∈ Gq.
(3) The dealer chooses randomly 
and defines the polynomial
(4) Let s = f (0) = a0 be the secret and let y = g5 (modp) be made public.
(5) The dealer chooses randomly pairwise distinct elements 
and calculates the partial secrets 
for the participants Ai. The values xi are published.
(6) The dealer calculates for each participant Ai the values 
(mod p) and zi ≡ gμi (mod p) and makes these public.
(7) To sign the protocol, each participant Ai chooses randomly ki ∈ and calculates ri μ gki (modp). The value ri will be sent to the other participants.
(8) Suppose that t participants have sent their values, say, A1,…, At have sent their values r1,…,rt. Then participant A; with 1 < i < t calculates the value
and the value
Then Ai has his partial signature
(9) The dealer verifies the partial signatures by checking if
(Recall that ri = gki (mod p) and yi = gsi (mod p).)
In this case the dealer then calculates a = (c1 + … + ct) (mod q). The signature of m ∈ M is then
(10) The verification of the signature is to calculate
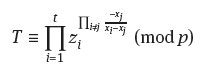
and check if
Notice that the set {A1,…, At} has to be given. However, given such a set the participants practically cannot cheat and the dealer can realize this. The signature is correct. Further, in this protocol, which verifies that the participants cannot cheat, it is difficult to discover any violations to the protocol by the dealer.
4.6 Zero-Knowledge Proofs
The final type of cryptographic procedure that we examine in this chapter is a zero- knowledge proof. We defer the technical definition to the end of this section. For the present, we say that a zero-knowledge proof or zero-knowledge protocol is an interactive method for one party to prove to another that a statement is true, without revealing any additional information.
The statement is usually mathematical in nature. In a zero knowledge proof the person proving is called the prover and the person who is shown the proof is the verifier. In encryption protocols, Alice and Bob, are usually used to stand for the communicating parties. In a prover and verifier protocol, for example a zero-knowledge proof, the prover is normally referred to as Peggy, while the verifier is called Victor. If proving the statement requires knowledge of some secret information on the part of the prover, a zero-knowledge proof implies that the verifier will not be able to prove the statement in turn to anyone else, since the assumption is that the verifier does not possess the secret information and does not learn anything about it. Notice that the statement being proved must include the assertion that the prover has such knowledge. (Otherwise, the statement would not be proved in zero-knowledge, since at the end of the protocol the verifier would gain the additional information that the prover has knowledge of the required secret information). If the statement consists only of the fact that the prover possesses the secret information, it is a special case known as zero-knowledge proof of knowledge.
For zero-knowledge proofs of knowledge, the protocol requires interactive input from the verifier, usually in the form of a challenge or challenges such that the responses from the prover will convince the verifier if and only if the prover does have the claimed knowledge. We have looked at this earlier in terms of password verification. In this case Victor is convinced that Peggy has the secret information but does not learn it himself. However, password verification lacks the crucial property of a zero- knowledge proof, namely the proof that Victor does not gain any information about Peggy’s password.
A zero-knowledge proof is usually not a proof in the mathematical sense but rather a probabilistic proof. For each challenge of the verifier, the prover has a certain probability of being correct purely by guessing. For each correct response by the prover, the probability of consistently correct guessing gets smaller. At the conclusion of the protocol the probability is very high that the prover does know the secret. This will become clearer in the examples below.
It remains to find a way for us to prove that, given a proposed zero-knowledge proof protocol, the verifies does not obtain any information about the secret. This can be achieved as follows: we show that the verifier can produce two recordings of the repeated challenge-and-response experiments. The first recording assumes that Peggy knows the secret and just documents the execution of the protocol. The second recording assumes that Peggy does not know the secret and is guessing her replies. In this case, the verifies records only the successful experiments when Peggy replies correctly and deletes the unsuccessful ones. Then the two recordings are shown to a neutral outside party, and we have to demonstrate that this outside party cannot distinguish the correct recording from the fake one. Then this certifies that the verifier did not receive any extra information during the correct execution of the protocol, as this extra information could be used to distinguish the two recordings.
In the following we present two examples of zero-knowledge proofs.
Example 4.6.1. The following setup is a standard prototype of a zero-knowledge proof of knowledge. We suppose that Peggy, the prover, has knowledge of the secret word used to open a magic door in a cave. She wants to verify to Victor, the verifier, that she does indeed have possession of this magic word without revealing any information about it. The cave is shaped like a rectangle, with the entrance on one side and the magic door blocking the opposite side.
Fig. 4.1: The Zero-Knowledge Cave.
The zero knowledge proof works as follows. Victor waits outside the cave (at point 4) as Peggy goes in. They label the left and right paths from the entrance 1 and 2. Peggy randomly takes either path 1 or 2. Then Victor signals into the cave the name of the path he wants Peggy to use to exit, either 1 or 2, chosen at random. Providing she really does know the magic word, this is easy: if necessary, she opens the door and arrives at point 3 along the desired path. Note that Victor does not know which path she took to get into the cave.
However, suppose that Peggy does not know the word. Then she is only able to return by the desired path if Victor happens to name the same path that she entered by. Since Victor chooses path 1 or 2 at random, she has a 50% chance of guessing correctly. If they repeat this process many times, her chance of successfully answering all of Victor’s requests is extremely small. In fact, after n repetitions it is (2 )n. Thus, if Peggy arrives at the correct exit many times, Victor can conclude that she is very likely to know the secret word.
Now let us prove the zero-knowledge property for this protocol. We assume that Victor produces two recordings of the experiments according to the above instructions. If the setup is created correctly, a neutral outside party cannot distinguish the recordings. Therefore we can conclude that Victor does not get any information (such as the time taken by Peggy to arrive at point 3 or the echo of her saying the magic word) from which he could deduce clues about the magic word.
A second example of a zero-knowledge proof of knowledge protocol is based on some number theory and is a numeric version of the cave example.
Example 4.6.2. In the following Diffie-Hellman Zero-Knowledge Protocol, Peggy proves to Victor that she knows a certain discrete logarithm (see Section 6.3 for more information on discrete logarithms).
(1) Peggy and Victor agree on a large odd prime number p and a primitive element g modulop withg ∈ {1,…,p - 1}. We then have 
.
(2) Peggy chooses a random integer a ∈ {1,…,p - 1} and calculates b = ga (mod p). She sends b to Victor and will prove to Victor that she knows a.
(3) Peggy chooses a random integer x ∈ {1,…, p - 1} and calculates y = g (modp). She sends y to Victor.
(4) Victor chooses (for the question) randomly an∈∈ {0,1} and sends it to Peggy.
(5) If ε = 0 then Peggy sends z = x to Victor. If ε = 1 then Peggy sends x + a modulo (p - 1) to Victor.
(6) If ε = 0 then Victor verifies that g = y (mod p), while If ε = 1 then Victor verifies that g = yb (mod p).
This method proves with probability 1 that Peggy knows a.If ε = 0 then
while If ε = 1 then
Hence the probability is 1 that Peggy does not know a. As in the cave example, given n rounds where Peggy is correct, there is only a probability of 
that she does not know a. The zero-knowledge property of this protocol follows in exactly the same way as above.
To conclude this section, we look more formally at zero-knowledge proofs. Assume that Peggy, the prover, has a secret m and that she has to prove to Victor, the verifier, that she knows m. Further, there is a probability distribution on Peggy’s responses to Victor’s challenges, so that there is a probability for each of Peggy’s responses to be correct. In addition, we assume that Victor’s challenges are independent. At the most basic level a zero-knowledge proof must satisfy three properties:
(1) Completeness: If the statement is true, the honest verifier (that is, one following the protocol properly) will be convinced of this.
(2) Soundness: If the statement is false, no cheating prover can convince the honest verifier that it is true, except with some small probability.
(3) Zero-Knowledge: If the statement is true, no cheating verifier learns anything other than this fact. This is formalized by showing that every cheating verifier has some simulator that, given only the statement to be proved (and no access to the prover), can produce a transcript that “looks like” an interaction between an honest prover and the cheating verifier.
The first two properties are present in general interactive proof systems. The third property is what makes the proof zero-knowledge. As can be seen and has been mentioned earlier, zero-knowledge proofs are not proofs in the mathematical sense of being deterministic proofs, but rather probabilistic proofs. In each zero-knowledge protocol, there is some small probability, the soundness error, that a cheating prover will be able to convince the verifier of a false statement. The assumption is that repeated applications of the interactive protocol will reduce the soundness error to a negligibly small value.
4.7 Exercises
4.1 Distribute the secret 42 using the Shamir secret sharing scheme evenly among three people such that any two can put together the secret.
4.2 The company Ruin Invest has two directors, seven department managers, and 87 further employees. A valuable customer file is protected by a secret key. Develop a procedure for the distribution of the information about the key among the following groups of authorized people:
(1) both directors together,
(2) one director and all seven department managers together,
(3) one director, at least four department managers, and also at least 11 employees.
4.3 A group of at least three employees of a company decides to calculate their average income and then to compare it to their own personal salaries. They are all honest but noone wishes to reveal his salary to the other employees. Describe a protocol to solve this problem.
4.4 Alice and Bob want to decide who among the two of them has the higher salary but neither wants to divulge their salary. Describe a protocol to solve this problem.
Hint: You may assume that there is a finite number of possible salaries.
4.5 Give a fair protocol for an electronic roulette game. You need not deal with the settings in detail.
4.6 Let p, q ≥ 3 be two large primes and n = pq. The integer n is odd so n = 2k +1 for some k ∈ N. Show that
by 
is a hash function with a trapdoor.
4.7 Two players are playing a game of internet chess. They will decide who plays white. Show how to do this with the help of a hash function,
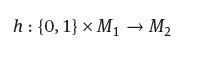
where M1, M2 are large sets and so that no partner can alter the decision at a later time.
4.8 This is the Shamir-No-Key Protocol.
(a) Consider the following protocol.
(1) A and B agree publically on a large odd prime p.
(2) A generates a pair (a, a’) ∈ × and aa’ = 1 (mod(p - 1)).
(3) B generates a pair (b, b’) ∈ × and bb’ = 1 (mod(p - 1)).
(4) A wants to send the plaintext m ∈ {1,2,…,p - 1} to B. To do this he calculates x = ma (modp) and sends this to B.
(5) B calculates y = xb (modp) and sends this to A.
(6) A calculates z = ya' (mod p) and sends this to B.
(7) B calculates m = zb' (mod p).
Show that this protocol is correct.
(b) Considering the protocol from part (a) show that if an attacker can find from , then the attacker can determine m.