Lemma 14.2.3. Let a be a word ordering on (X>, and let a be the restriction of a to (X>. Then also a is a word ordering.

Now we are ready to state and prove the main theorem of this section.

Theorem 14.2.4 (Computation of Elimination Ideals). LetL c X, let a be an elimination ordering for L, and let a be the restriction of a to (X>. Given a two-sided ideal I c K (X> and a a-Gröbner basis G of I, the set G = G n K(X> isaa-Gröbner basis of the elimination ideal ⁷ = I n K(X>.

Proof. It is clear that G is contained in 7 We have to show that the leading words of the polynomials in G generate the leading word ideal Lw₅(/). For f ϵ ⁷ {0|,we have Lw_a (f) = Lw_a (f) ϵ (X). Since G is a a -Gröbner basis of I, we find words w₁, w₂ ϵ (X> and g ϵ G such that Lw_a (f) = w₁ Lw_a (g)w₂. As this word is contained in (X>, it follows that w₁, w₂, Lw_a (g) ϵ (X>. From the hypothesis that a is an elimination ordering, we get that g ϵ K (X>, and therefore g ϵ G. This was to be shown.

A first application of this theorem is the following method for computing the intersection of two-sided ideals in K(X>.

Proposition 14.2.5. Letf₁,…,f_s,g₁,…,g_t ϵ K(X>,letI = (f₁,…,f_s> andJ = (g₁,…, g_t > be the two-sided ideals generated by these non-commutative polynomials, and lety be a further letter. Then we have

I J = (yf1,…,yfs,(1 − y)g1,…,(1 − y)gt,yx1 .x1y,…,yx_n .x_ny.K(x)

In particular, a system of generators of the intersection ideal I n J can be enumerated using the Buchberger Procedure.

Proof. Given h ϵ I n J,we can write h = p₁f₁p’₁ + … + p_sf_sp’_s and h = q₁g₁q’₁ + … + q_tg_tq’_t with p_;,p., q_;-, q| ϵ K(X>. Then we have

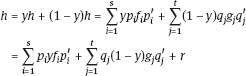
with a polynomial r ϵ (yx₁ − x₁y,…, yx_n − x_ny>. Hence h is contained in the right-hand side of the claimed formula.

Conversely, let h be contained in this right-hand side. Then we have p_;, p-, q_;-, q’j ϵ K(X,y> such that h = £^s₌1 pyfp- + j q_s(1-y)g_;q| + rwith r ϵ Ox-x_;y | i = 1,…, n>. Substituting y 1 in this representation shows h ϵ I, and substituting y 0 shows h ϵ J. □

It is clear that this proposition can be extended to intersections of finitely many twosided ideals in K (X> in a straightforward way. The main application of elimination is the possibility to compute kernels and images of K-algebra homomorphisms. For this purpose we use the following setting.

Let Y = {y₁,…,y_m| be a further set of letters, and let I c K(X> and J c K(Y > be two-sided ideals. We consider a homomorphism of K-algebras

0 : K(X>/I K(Y>/J

given by 0 (x_;) = f with f ϵ K (Y> for i = 1,…, n.

Proposition 14.2.6 (Kernels of Algebra Homomorphisms). The kernel of0 satisfies

Ker(0) = (((X1 -f1, …,x_n − f_n> + J • K(X, Y>) n K(X>) + I.

In particular, it can be enumerated by applying the Buchberger Procedure to compute this elimination ideal.

Proof. Given g ϵ K(X> such that g ϵ Ker(0), we have g(f₁,… ,f_n) ϵ J. By replacing f by (fi − X_;) + Xi in this equality and multiplying out, we obtain g = h + g(f₁,… ,f_n) ϵ (X₁ − f₁,…, x_n − f_n> + J where h ϵ (x₁ − f₁,…, x_n − f_n>. Hence g is contained in the right-hand side.

Conversely, let g ϵ K(X> be such that g is contained in the right-hand side. Then there exist p_;, p • ϵ K(X, Y> such that g = pi X − fi)p[ + h with h ϵ J • K(X, Y>. Substituting Xj fj in this equality shows g(f₁,… ,f_n) ϵ J, and therefore g ϵ Ker(4>).

One application of this procedure is that we have a semi-decision procedure for checking whether an element f of a finitely generated algebra K(X>/I is algebraic or transcendental over K. Namely, we can apply the preceding proposition to the K-algebra homomorphism

0 : K[z] —> K(X>/I given by z f.

If the procedure finds a non-trivial element in Ker(0), we can also compute the minimal polynomial off, i.e., the monic polynomial which generates Ker(0).

Another application of the preceding proposition is a semi-decision procedure for checking if an element of a monoid or group has a finite order. This can be done as follows.

Remark 14.2.7. Let G = (x₁,…,x_n;r₁ = … = r_m = 1> be a finitely presented monoid having the cancellation property or a monoid presentation of a finitely presented group. Then the monoid ring over Z₂ satisfies Z₂[G] = Z₂(X)/I where I = (r₁ − 1,…, r_m − 1) .Let w ϵ (X) be a word representing an element W of G.

To check whether the order of m is finite, we choose an additional letter y and form the ideal J = (y − w, r₁ -1,…, r_m -1) in Z₂ (X, y). Then we let a be an elimination ordering for X and start the computation of a a -Gröbner basis G of J.

(1)  If we have G nZ₂|y] =0 at some point during the computation, the element W is algebraic over Z₂. Since the ideal J is generated by binomials, its Gröbner basis consists of binomials. Thus the minimal polynomial of W is of the form Z^k + z^e with 1 < k <1. Since G has the cancellation property, it follows that W^l-k = 1. Notice that in this case we can compute the order of W.

(2)  If the computation finishes with a Gröbner basis G with G nZ₂ [y] = 0 then we have Ker(ty) = {0} and the element W has infinite order.

The next proposition provides a semi-decision procedure for checking if an element is in the image of an algebra homomorphism, and yields a preimage if the answer is positive.

Proposition 14.2.8 (Images of Algebra Homomorphisms). Letty : K(X)/I —> K(Y)/J be a K-algebra homomorphism With ty (x¡) = f¡ as above. LetD c K(X, Y) be the diagonal ideal

D = (X1 − f1,…,x_n − f_n) + J • K(X, Y),

let a be an elimination ordering for Y, and let Gbea a-Gröbner basis ofD.

(1)  Forg ϵ K(Y), the element g is contained in the image ofty if and only if NR_{a G}(g) ϵ K(X), i.e., if and only if this normal remainder does not involve any letter from Y.

(2)  Given g ϵ K (Y) such thatg’ = NR_{a G}(g) is contained in K (X), We have g = ty (g’).

Proof. First we let g ϵ K (Y) such that y’ = NR_{a G}(g) ϵ K(X). Then there exist elements Pi,p’ ϵ K(X, Y) and q ϵ J • K(X, Y) such that g − g’(/!,… ,/J = £”1 p¡(x¡ − f )p’ + q. Substituting x¡ f in this equality yields g-g’ (f₁,…,f_n) ϵ J, and therefore g = ty (g’).

Conversely, let g ϵ K(Y) be such that g is contained in the image of ty. Then there exists a polynomial h ϵ K(X) such that g + J = h(f₁,… ,f_n) + J. Since we have h + D = h(f₁,… ,f_n) + D,wegetg − h ϵ D, and hence NR_{a G}(g) = NR_a>G(h). Now the facts that h ϵ K (X) and that a is an elimination ordering for X imply NR_{a G} (g) ϵ K (X). □

Based on this proposition, the Buchberger Procedure yields a semi-decision procedure for the Subalgebra Membership Problem: given a finitely generated K-subalgebra S = K(f₁,… ,f_n) of a K-algebra K(Y)/J, decide whether a given residue class g is contained in S. In the YES case, i.e., if we have g ϵ S, this will be detected in finitely many steps and the procedure returns an explicit representation of g in terms of the generators {f₁,… ,f_n} of the subalgebra S. Otherwise, the procedure may or may not stop.

In group theory, the proposition allows us to semi-decide subgroup membership as follows.

Remark 14.2.9. Let G = (x₁,…,x_n;r₁ = … = r_m = 1> be a finitely presented group, and let H c G be the subgroup generated by the residue classes of some words h₁,…,h_k ϵ (X>. The subgroup membership problem (or the generalized word problem) asks us to decide whether a given word w ϵ (X> represents an element of H. The following instructions define a semi-decision procedure for this problem.

(1)  Let {y₁,…, y_n} be further letters. Consider the presentation

Z₂[G] = Z₂(x1,…,x„,x’₁,…,x’_n>/(r_; − 1, Xjyj − 1,yjXj − 1>;=1,…,m. ;=1,…,n

(2)  Using the subalgebra membership test, check whether we have W − 1 ϵZ₂ (h₁ − 1,…, h_k -1> inside Z₂ (X, Y>/I,whereI is the defining ideal for Z₂[G] given above.

To prove correctness of this method, we still have to check that W ϵ H is equivalent to W − 1 ϵZ₂(h₁ − 1,…,h_k − 1>.Let W = h,- …h. We proceed by induction on s and find that

W − 1 = h · h_; _₁ − 1)h_!s + (h_!s − 1) ϵ2h − 1,…, hk − 1>.

For a proof of the reverse implication we refer to [MR], Theorem 9.

To use Gröbner bases for other hard problems underlying non-commutative cryptography (such as the problems explained in Section 9.8), we need to generalize Gröbner basis theory from two-sided ideals in K (X> to two-sided submodules of a free module over this ring. In particular, we need the concept and calculation of syzygies. These topics are introduced in the next section.

14.3 Gröbner Bases of K(X>-Modules

Let K be a field, let X = {x₁,…,x_n| be a set of letters, and let K(X> be the noncommutative polynomial ring over K in the indeterminates x₁,…, x_n. The enveloping algebra K(X>^env = K(X> <% K(X> is a two-sided module over K(X> in the obvious way: for A, f2, g1, g2 ϵ K (X>, we letf ® g2)/2 = fg ® g2.

In the category of all two-sided K(X>-modules, the enveloping algebra K(X>^env plays the role of a free module of rank 1: given any two-sided K(X>-module M and an element v ϵ M, there is a unique homomorphism of two-sided K(X>-modules 0: K(X>^env —> M such that 0 (1 ® 1) = v. Consequently, for every r > 1, the two-sided K(X>-module F_r = ©r₌₁ K(X>^env is a free module of rank r in this category. For i = 1,…, r,welet e_; = (0,…, 0,1 ® 1,0,…, 0) where 1 ® 1 occurs in the i-th position.

In this section we extend the Gröbner basis theory for two-sided ideals in K (X> to a Gröbner basis theory for two-sided submodules of F_r. The main motivation for this is the following notion.

Definition 14.3.1. Let M be a two-sided K(X>-module, let v₁,…, v_r ϵ M, and let 0: F_r —> M be the uniquely determined homomorphism of two-sided K(X>-modules satisfying 0 (e,) = v, for i = 1,…, r. Then the two-sided K(X>-submodule

is called the (two-sided) syzygy module of (v₁,…, v_r).

The computation of syzygy modules is a fundamental technique in computational algebra and is used frequently in non-commutative cryptography. Let us start the development of Gröbner basis theory in this setting.

Definition 14.3.2. A term in F_r is an element of the form we_iw’ where W, W’ ϵ (X> and 1 < i < r. The set of all terms in F_r is denoted by T(F_r).

A module term ordering on T(F_r) is a total ordering T such that t₁ <_T t₂ implies w₁t₁w’₁ <_T w₂t₂w2 for all t₁, t₂ ϵ T(F_r) and all W₁, w1, W₂, w2 ϵ (X> and such that T is a well-ordering.

Starting from a word ordering on (X>, we can define module term orderings as follows.

Example 14.3.3. Let To be a word ordering on (X>.

(1)  For terms W₁e_;W^,₁, W₂ejW’₂ ϵ T(F_r) such that W₁, w1, W₂, w2 ϵ (X> and i,j ϵ {1,…,r|,welet

This defines a module term ordering ToPos on T(F_r).

(2)  For terms w₁e_iw’₁,w₂e-w’₂ ϵ T(F_r) such that w₁,w’_vw₂,w2 ϵ (X> and i,j ϵ {1,…,r|,welet

Again this defines a module term ordering PosTo on T(F_r).

Given a module term ordering, the following terminology generalizes the usual definitions of leading terms etc.

Definition 14.3.4. Let T be a module term ordering on T(F_r).

(1)   Givenavector v ϵ F_r{0|, there exists a unique representation v = c₁f₁ + … + c_st_s with c₁,…,c_s ϵ K {0| and t₁,…,t_s ϵ T(F_r) satisfying t₁ >_T … >_T t_s .The term Lt_T (v) = t₁ is called the leading term of v with respect to T . The element Lc_T (v) = c₁ is called its leading coefficient.

(2)   For a two-sided submodule M c F_r, the two-sided submodule Lt_T(M) = (Lt_T (v) | v ϵ M {0|> of F_r is called the leading term module of M.

(3)  A subset G of a two-sided submodule M of F_r is called a T-Gröbner basis of M if the leading term module Lt_T (M) is generated by the leading terms Lt_T (f) such that f ϵ G.

Based on these definitions, many standard results of Gröbner basis theory generalize in a straightforward way. Let us mention three of them. For detailed proofs we refer the reader to [BK], Section 2.

Proposition 14.3.5 (Macaulay’s Basis Theorem). LetM be a two-sided submodule of F_r. Then the residue classes of the elements in T(F_r) Lt_T (M) form a K-vector space basis ofF^r /M.

Proposition 14.3.6 (The Division Algorithm). Let s > 1, and let m,f₁,…, f_s ϵ F_r {0|. Consider the following sequence of instructions.

(1)  For i = 1,…, sletkj = 1, g_;1 = g = 0,p = 0 and v = m.

(2)  Find the smallest i ϵ {1,…,s| suchthat Lt_T (v) = w Lt_T (fj)w’ for some w, w’ ϵ (X>.

If such an i exists, increase s by 1, set g_jk. = Lcifl w, g’_ik = w’ and replace v by

v − wfjW¹ . If now v = 0, continue with step 2. Otherwise, continue with step 4.

LCT ^(fi⁾

(3)  Replace p by p + Lc_T (v) • Lt_T (v) and v by v − Lc_T (v) • Lt_T (v). If now v = 0, continue with step 2.

(4)  Return the tuple ((g_n,g11),…, (g,g),…, (gs1,g),…, (gsk_s,g’_Sk_s)) and thevec- torp ϵ F_r.

This is an algorithm which returns elements ((g₁₁,g1₁),…, (g_sk , g_sk )) and p such that the following conditions are satisfied.

(1)  We have m = £^s₌1 £* = ₁ gfgj + p.

(2)  No element of Supp(p) is contained in (Lt_T (f₁),…, Lt_T (f_s)>.

(3)  Ifgy = 0 = gj for some i ϵ {1,s| and j ϵ {1,k,-| then we have Lt_T (gf-gj) <_T Lt_T (m).

(4)   For all i ϵ {1,…, s| andj ϵ {1,…, k_;| we have

gj-Ltr (fi)g’ijt (LtT (fi),…, LtT(fi-1)>-

(5)  The elements ((g₁₁, g1₁),…, (g_sk , g_sk )) andp are uniquely determined by the preceding conditions (1)-(4).

Definition 14.3.7. Let G = (g₁, …,g_s) be a tuple of elements g_t ϵ F_r.

(1)  A pair (i, j) with i, j ϵ {1,…, s| and i < j is called a critical pair of G if there exist words Wj, w-, Wj, w- ϵ (X> such that Wj Lt_T(g_i)w’_i = Wj Lt_T (g_;)w|, such that Wj and Wj have no common prefix, and such that w- and wj have no common suffix.

(2)  For every critical pair (i, j) of G, the element

is called the S-vector of gj andgj.

Proposition 14.3.8 (Buchberger’s Criterion). Let G = {g | i ϵ I| be a (countable) set of elements in F_r which generate a two-sided submodule M = (G> ofF_r, and let B be the set of critical pairs between elements of G. Then the set G is a t-Gröbner basis ofM if and only if NR_{t G}(S,j) = 0 for all (i, j) ϵ B.

Finally, we are ready to formulate the module analogue of Buchberger’s Procedure.

Theorem 14.3.9 (Buchberger’s Procedure for Modules). Let G = {g₁,… ,g_s| be a finite set of elements in F_r {0| which generates a two-sided K (X>-submodule M = (G> ofF_r. Consider the following sequence of instructions.

(1)  Let H = G, let B be the set of critical pairs ofH, and let s’ = s.

(2)  If B = 0, return G and stop. Otherwise choose a pair (i, j) ϵ B using a fair strategy and delete it from B.

(3)  Compute the S-vector Sj and its normal remainder NR_{t h}(S,j). If the result is zero, continue with step 2.

(4)  Increase s’ by one. Appendg_s, = NR_{t h}(S,j) to H, and append the elements of {(i, s ‘) | 1 < i < s ‘ and (i, s ‘) is a critical pair| to B. Continue with step 2.

This is a procedure which enumerates a tuple H ofvectors whichform a T − Gröbner basis ofM. IfM has a finite T- Gröbner basis, the procedure stops after finitely many steps and the vectors of the resulting tuple H form a finite T-Gröbner basis ofM.

A proof using the current notation and terminology is contained in [BK], Section 2. Moreover, it is shown there that Gröbner bases for two-sided submodules of F_r generalize Gröbner bases for two-sided ideals in K(X> in the following way: under the epimorphism n : F₁ —> K(X> given by e₁ 1, two-sided submodules of F₁ containing (x₁e₁ − e₁x₁,.. .,x_ne₁ − e₁x_n> correspond uniquely to two-sided ideals in K(X>, and their Pos-o Gröbner bases correspond to o-Gröbner bases of their images in the obvious way.

It is clear that the Buchberger Procedure for Modules results in a semi-decision procedure for submodule membership. Since this in completely analogous to the ideal case, we leave it to the interested reader. Besides the analogues of the applications of Gröbner bases introduced in Section 4.2, we have one new application which is particular to modules and which is explained next.

In the following we let L be a subset of {1,…, r|, and we let F_r denote the free two-sided K(X>-module generated by {e_; | i ϵ {1,…, r| L|.

Definition 14.3.10. A module term ordering t on T(F_r) is called a component elimination ordering for L if every element m ϵ F_r {0| such that Lt_T (m) ϵ F_r is contained in F_r.

Let M c F_r be a two-sided submodule. The two-sided submodule M n F_r of F_r is called the component elimination module of M with respect to L.

The following example shows that component elimination orderings exist.

Example 14.3.11. Let i ϵ {1,…, r|, and let L = {1,…, i|. If o isa term ordering on (X> then the module ordering T = Pos-o is a component elimination ordering for L. Namely, let m ϵ F_r {0| be such that Lt_T (M) = w₁ejw^,₁ ϵ F_r. Then every term t = w₂e_kw’₂ ϵ Supp(m) satisfies t <_T Lt_T(m). This implies k > j, and we conclude that t ϵ F_r and m ϵ F_r.

The following proposition shows how one can compute component elimination modules. In fact, it yields a Gröbner basis with respect to the restriction to F_r of the given component elimination ordering.

Proposition 14.3.12 (Computing Component Elimination Modules). Let M be a twosided submodule ofF_r, letLc {1,…, r|, and let T be a component elimination ordering for L. Furthermore, let G be a T-Gröbner basis o M, and let F be the restriction of T to T(F_r). Then the setG = G n F_r is a T-Gröbner basis ofM n F_r.

Proof. Let m ϵ (M n F_r) {0|. Then we have Lt_f (m) = Lt_T(m) ϵ Lt_T(M) because F is the restriction of T . Since G is a T-Gröbner basis of M, there exists an element g ϵ G such that Lt_f (m) = w Lt_T (g)w’ for some w, w’ ϵ (X>. But then we have Lt_T (g) ϵ F_r, and the assumption that T is a component elimination ordering for L yields g ϵ F_r, i.e., g ϵ G = G n F_r. Now the fact that Lt_T (g) = Lt_f (g) concludes the proof. □

Module component elimination is the key ingredient for the computation of syzygies in a non-commutative setting. Recall that the two-sided syzygy module Syz(G) of a tuple G = (g₁,…, g_s)of elements of F_r was defined as the kernel of the homomorphism A : F_s —> F_r of two-sided K(X>-modules which is given by £, gj for i = 1,…, s. The computation of two-sided syzygy modules is based on the following proposition.

Proposition 14.3.13. LetF_r+s be the free two-sided K(X>-module of rank r + s, and let {e₁,…, e_r+_s| be its canonical basis. Let G = (g₁, …,g_s) be a tuple of elements ofF_r {0|, letF_r+_s = (e_r+1,…, e_r+_s>, and for every m ϵ F_r let m denote the corresponding element in F_r+s under the canonical injection e, e,. Let U be the two-sided submodule ofF_r+s generated by {g₁ − e_r+1, …,g_s − e_r+_s|. Then we have

U n F_r+_s = Syz(G).

In particular, we can enumerate the syzygy module Syz(G) using module component elimination.

Proof. Let us consider the homomorphism 0 : F_r+_s —> F_s given by e_r+j £, for i = 1,…,s. By restricting 0 to U n F_r+_s, we obtain an injective homomorphism p. Therefore it suffices to prove that the image of p is Syz(G). Let m = Zs₌₁ Zj_eN wWy be an element of Syz(G) with c¡j ϵ K and w,j, wj ϵ (X> for i = 1,…, s. Notice that for every j ϵ N, all but finitely many of the elements c,j are zero. Then the element ^m = Z^Si=1 ZjN ^cij^wij^er₊i^w’ij = Z^Si=1 ZjN ^cy^wy^gi^wy^-Z^s=1 ZjN ^cij^wij(g^-er₊i^)w’ij^{is contained} in U n F_r+_s, and it satisfies p (m) = m.

Now suppose that U n F_r+_s contains m = Zs₌₁ Zj_eN c,jW,je_r+jwj. Then we have ^{A (}P^(m)) = ^Zs=1 Z’gN ^cij^wij^gMj = ^Zs=1 ^Zj6N ^{- e}r+i^)wij + ^Zs=1 ^Zj6N ^cij^wij^er₊Mj ^ϵ U. Moreover, none of the generators e_r+1,…,e_r+s appears in the representation of A (p(m)). Since U is generated by the elements {g₁ − e_r+1,…,g_s − e_r+_s|, this implies A (p(m)) = 0. Hence we get p (m) ϵ Syz(G).

Using this result, it is easy to formulate a procedure for the computation of a two-sided syzygy module.

Corollary 14.3.14 (Computing Two-Sided Syzygy Modules). Letg₁,…,g_s c F_r {0|, and let G = (g₁,… ,g_s). Let p : F_r+_s —> F_s be the homomorphism defined by e_r+j £, for i = 1,…, s, and for every m ϵ F_r let m denote the corresponding element in F_r+s. Consider the following sequence of instructions.

(1)  Choose a component elimination ordering T for L = {1,…, r| on T(F_r+s).

(2)  Compute a T-Gröbner basis H of the two-sided submodule U = (g₁ − e_r+1, …,g_s -

^er+s> ^ofFr+s.

(3)  Compute H = H n F_r+s. Return p (H) and stop.

This is a procedure which enumerates a T -Gröbner basis of the two-sided syzygy module Syz(G), where T is the restriction ofT to T(F_r+s).

Proof. By the above proposition, the two-sided module UnF_r+_s is isomorphic to Syz(G). Since U n F_r+_s is also the component elimination module of U with respect to L, Proposition 14.3.12 implies the claim.

Using the computation of two-sided syzygies, we arrive at the following Gröbner basis algorithm for solving the Conjugator Search Problem (CSP) in certain finitely presented groups. This problem has been used as a basis for group-based cryptosystems in previous chapters.

Problem CSP: Given a group G and two elements g, h ϵ G which are known to be conjugated to each other (i.e., such that there exists an element a ϵ G for which ag = ha), find a conjugator (i.e., find such an element a).

In the sequel we make the following assumptions.

(1)  The group G is finitely presented: G = (x₁,…, x_n; r₁ = … = r_m = 1>

(2)  There exists a word ordering o on (X> such that R = {r₁ − 1,…, r_m − 1| is a o- Gröbner basis of the defining ideal in Z₂ (X> of the group ring Z₂ [G].

Thus we can use R to represent the residue class of a word w ϵ (X> in G uniquely by its normal remainder NR_o r(W). In particular, we can use R to solve the word problem in G effectively. In this setting, the following algorithm solves CSP in G. We outline its proof which is based on the results of this section. For the full details, we refer to [BK], Section 5.

Proposition 14.3.15 (The Conjugator Search Algorithm). In the setting described above, let w, W ϵ (X) be two words representing conjugated elements of the group G. Consider the following sequence of instructions.

(1)  Let F₆ be the free two-sided module ofrank 6 over K(X). In F₆ form the two-sided submodule

U = (ew − e₃, e_xw’ − e₄, e₂ − e₃ − e₅, e₂ + e₄ + e₆,

e_l(w_l − w[),…, e_x(w_t − w’_t), e₂(w_l − w),…, e₂(w_t − w’_t),

x-e-i − e₁x₁,…,x„e₁ − e₁x_n,x − e2x₁,…,x„e2 − e2x_n).

(2)  Choose the following module term orderingr on T(F₆):for t₁, t1, t₂, t2 ϵ (X), let

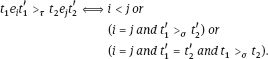
Compute an interreduced two-sided T-Gröbner basis H ofU.

(3)  In H there exist elements whose leading term is of the form t¡e₅ where t¡ ϵ (X) is the normal remainder with respect to R. Return the words t_{ and stop.

This is an algorithm which solves the Conjugator Search Problem in G.

Proof. It is clear that the module term ordering T defined in step 2 is an elimination ordering for both L = {1,2} and L’ = {1,2,3,4}. Hence the elements of H n (e₅, e₆) form a Gröbner basis of the intersection of Syz(w, w’) and Syz(1, -1).

By assumption, there exists a word a ϵ (X) representing a conjugator such that aw = w’ a. Therefore ae₅ − e₆a represents a syzygy in Syz(w, w’) and is contained in U. In particular, there exists an element h ϵ H whose leading term is of the form Lt_T (h) = te₅ with t ϵ (X). Since the elements (W¡ − w- )e₅ are all contained in U, we may assume that the word t is a normal remainder with respect to R.

Observe that we can consider the computation of Syz(w, w’) n Syz(1, -1) as the composition of the computation of the two individual syzygy moduls combined with the computation of the intersection of two submodules. For all three Gröbner basis computations, we start with a system of generators consisting of binomials. Hence also the computed Gröbner bases consist of binomials. Consequently, the element h ϵ H found above is of the form h = te₅ + be₅c or h = te₅ + b’ e₆c’. In the first case, the definition of T yields c =1 and t >_a b. This contradicts the fact that we assumed t to be a normal remainder with respect to R. Therefore only h = te₅ + b’ e₆c’ is possible. Here u ϵ Syz_K[_G](1, -1) yields t = b’ c’. Hence the element a = (b’)^-1t satisfies ae₅ − e₆a = (b’)^-1u ϵ Syz_K[_G](w, w’). Thus the word a ϵ (X) represents the desired conjugator.

Let us recall that the computation of the Gröbner basis necessary in step (2) is an enumerating procedure. After a new Gröbner basis element has been found and fully interreduced, we can check whether it has the shape required by step (3). Since we assume that w and w’ are conjugates, a suitable element u will be discovered eventually, i.e., our instructions can be performed in such a manner that they define an algorithm.

Up to now, we have used non-commutative Gröbner bases mainly to deal with the computational problems mentioned in Section 9.8 effectively. In the final section of this chapter, we use them to construct cryptosystems whose security relies on the difficulty of computing certain Gröbner bases.

14.4 Non-Commutative Gröbner Basis Cryptosystems

As mentioned previously, the worst-case bounds for the complexity of computing a Gröbner basis are very high. This has led many researchers to suggest cryptosystems whose security is based on the difficulty of computing a certain Gröbner basis. Initial attempts at doing this via commutative polynomials met with a lot of skepticism and mixed success. However, generalizing the approach to submodules of two-sided free modules over the non-commutative polynomial ring provides sufficient freedom to define cryptosystems which are resistant to all known attacks. In fact, in this section we show that moving from polynomial rings to modules over polynomial rings has the added advantage that we can include the operation of a group (or a ring) on a finite (or countably infinite) set in the encryption algorithm. In this way, we can show that all public key cryptosystems discussed in the earlier chapters of this book are special cases of Gröbner basis cryptosystems.

To define the most general kind of Gröbner basis cryptosystem, we use a setting which is slightly more general than that of the preceding sections. Instead of working over the non-commutative polynomial ring K(X>, we work over a monoid ring K[M] where M is a finitely presented monoid defined by a convergent rewriting system, i.e., such that the defining ideal of K[M] has a finite Gröbner basis. Of course, the noncommutative polynomial ring is then nothing but the special case of a free monoid M. More precisely, we consider the following setting.

Let X = {x₁,…, x_n| be a finite alphabet, and let M = (x₁,…, x_n;l₁ = r₁,…,l_m = r_m> be a finitely presented monoid. Then the monoid ring K[M] satisfies K[M] = K(X>/I_m, where I_M is the two-sided ideal generated by R = {l₁ − r₁,…,l_m − r_m|. We assume that there exists a word ordering o on (X> such that R is a o-Gröbner basis of I_M and I, >_o r, for i = 1,…, m. Consequently, we can represent every element of M by a word w ϵ (X>, and there is a unique representation by a word NR_or(w) which is in normal form, i.e., the normal remainder w.r.t. R of some other word representing the same monoid element.

Furthermore, we let r > 1 and F_r = (K[M] ®K[M])^r the free two-sided K[M]-module of rank r. The standard basis of F_r is denoted by {e₁,…, e_r|. Let T be a module term ordering on T(F_r), and for a two-sided submodule U of F_r we let O_T (U) = T(F_r) Lt_T (U).

Definition 14.4.1. A (general, two-sided) Gröbner basis cryptosystem consists of the following data.

(1)  Public Information: the monoid presentation of M,the free two-sidedmodule F_r, a subset S of the set O_T (U), and finitely many elements u₁,…,u_s ϵ U.

(2)  Secret Information: a T -Gröbner basis G of a two-sided submodule U of F_r.

(3)  Encryption Procedure: A plaintext unit is an element m ϵ {S>_K. The corresponding ciphertext unit is c = m + f₁u₁g₁ + … + f_su_sg_s with suitably (e.g. randomly) chosen elements f,,gj ϵ K[M].

(4)  Decryption Procedure: Compute m = NR_{t G}(c).

The correctness of this cryptosystem follows from the fact that every element of F_r has a unique normal remainder with respect to G and this normal remainder is contained in (O_T (U)>_K. Notice that the correct choice of the elements f,, gj ϵ K[M] in the encryption procedure is crucial for the security of the cryptosystem. It depends on the concrete setting in which this cryptographic primitive is used. For some settings this issue will be discussed later in this section. A similar definition of Gröbner basis cryptosystems is used in [AKr], but it relies on one-sided rather than two-sided modules. However, most remarks and constructions carry over from this case to the two-sided case without problems.

Next we collect some easy remarks about properties and variations of Gröbner basis cryptosystems.

Remark 14.4.2. Let a Gröbner basis cryptosystem be given as above.

(1)  If an attacker can compute G, he can break the cryptosystem. In general, the computation of Gröbner bases is EXPSPACE-hard.

(2)  The attacker knows u₁,…,u_s and S, but not a system of generators of U. We can make his task difficult by choosing u₁,…,u_s such that a Gröbner basis of (u₁,…, u_s> is hard to compute.

(3)  The advantage of using modules (rather than two-sided ideals in K (X>) is that one can encode hard combinatorial or number theoretic problems in the action of the terms on the canonical basis vectors (see the examples below).

(4)  The free module F_r is not required to be finitely generated. Any concrete calculation will involve only finitely many components.

(5)  We shall also consider the following variant: for the ciphertext unit we construct a pair c = (f₀, mf₀ + f₁u₁g₁ + … + f_su_sg_s) wheref₀ ϵ K[M] is a further randomly chosen element. Then the decoding procedure consists of computing NR_{t g} (mf₀ + f₁u₁g₁ + … + f_su_sg_s) = NR_{t >G}(mf₀) and “dividing” by f₀ to obtain m. In this way we achieve some additional data hiding: the summand mf₀ on the right hand-side resembles the other summands. However, there is no general method for performing the “division” NR_{t G}(mf₀) ^ m. We have to provide an explicit procedure in every individual example.

In the following we give some examples of Gröbner basis cryptosystems. In particular, we show that many classical cryptosystems can be realized as special cases.

Example 14.4.3. Let K = F_q be a finite field, where q = p^e with a prime number p and e > 0. Let M be the monoid M = N” = (x₁,…,x_n; x,xj = XjX, = 1forall i, j>.Weusethe module F₁ and submodules containing (x,e₁ - e₁x_i>, i.e., ideals in the commutative polynomial ring K[M] = K[x₁,.. .,x_n]. Choose a point (a₁,…, a_n) ϵ K”. Let U = (x₁ - a₁,…,x_n - a_n> and choose elements u₁,…,u_s ϵ U such that u,(a₁,…,a_n) = 0 for i = 1,…, s. Consider the following Gröbner basis cryptosystem.

(1)  Public information: The polynomial ring K[x₁,.. .,x_n], a term ordering T on T”, the set O_T(U) = {1|, and the polynomials u₁,…, u_s.

(2)  Secret key: The point (a₁,…,a_n) ϵ K” corresponding to the Gröbner basis G = {x₁ - a₁,…, x_n - a_n| of the ideal U.

(3)  Encryption procedure: A plaintext unit m ϵ K is encrypted as the polynomial c = m + u₁f₁ + … + u_sf_s with randomly chosen polynomials f₁,…, f_s ϵ K[M].

(4)  Decryption procedure: Compute m = NR_{t G}(C) = c(a₁,…, a”).

Clearly, this is Neal Koblitz’ Polly Cracker Cryptosystem from Section 13.2. Unfortunately, it allows many dangerous attacks, as we have seen in Section 13.3.

A number of improvements of Koblitz’ original approach have been proposed. Many of them fit our scheme.

Example 14.4.4. In the setting of the preceding example, choose a second commutative polynomial ring Q = K[y₁,…,y_m] and polynomials g₁,… ,g_m in K[M]. In this way there is a K-algebra homomorphism 0 : Q —> K[M] given by 0 (y,) = g, for i = 1,…,m. Choose a point (<₁,…,<_n) ϵ K” and elementsf₁,…,f_s ϵ Q such that 0 (f₁),…, 0 (f_s) ϵ U = (x₁ - <₁,…,X” - <“>. Now construct the following Gröbner basis cryptosystem.

(1)  Public information: The rings K[M] and Q, the homomorphism 0, the term O_T(U) = {1|, and the polynomialsf₁,…, f_s ϵ Q.

(2)  Secret key: The point (<₁,…, <_n) ϵ K”, or equivalently, the Gröbner basis {x₁ - <₁, …, X” - <“| of the ideal U in K[M].

(3)  Encryption procedure: We proceed in a similar way to the variant above. A plaintext unit is an element m ϵ K. We choose random polynomials h ϵ (1,… ,f_s>, a polynomial h’ ϵ Ker(0), and a random exponent K ϵ N”. Then we send c = (y^K, my^K + h + h’) where y = (y₁,.. .,y_m). In other words, an attacker knows the pair (0 (y)^K, m0 (y)^K + 0 (h)).

(4)  Decryption procedure: Compute v = [m0(y)^K + 0(h)](<₁,…,<_n) = m0(y)^K • (<1, …,<“) and obtain m = v/[0 (y)^K(<1, …,<“)].

This is Le van Ly’s Polly Two Cryptosystem (see [vLy]). Compared to Polly Cracker, it has the advantage that the usual linear algebra attacks do not work. It appears that an attacker has no choice but to compute a (possibly hard) Gröbner basis. Supposedly hard concrete instances of this cryptosystem have been suggested, but were not able to withstand side-channel attacks.

Now we show that the RSA Cryptosystem is in fact a Gröbner Basis Cryptosystem.

Example 14.4.5. Let K = Z₂, let X = {x,y|, and let M = N² = (x,y;xy = yx>. Then K[M] = K[x, y] is the commutative polynomial ring in two indeterminates. Moreover, let p, q » 0 be two distinct prime numbers, let n = pq, and let n = be the set of residue classes prime to n. We use the free module F_n = ©”=0 K[x, y] e, and the term ordering T = deglex-pos. Choose a number e ϵ Zjp_₁)(_q_₁) and compute the inverse d 0^{of £ in Z}(p_1)(q_1).

(1)  Public information: The module F_n (and thus the number n), the set O_T (U) = {e₀,…, e_n_₁1, the number e, and the vectors {u₁,…, u_s| = {e,x - e_j£modn | i = 0,…, n - 1|u {e,xy - e, | i = 0,…, n - 1|.

(2)  Secret key: The secret key consists of the primes p and q and the number d. Equivalently, the secret key is the T-Gröbner basis G = {u₁,…, u_s| u {e,y - e,d_modn; i = 0,…,n - 1| of U = (G>.

(3)  Encryption procedure: A plaintext unit is a vector e_m ϵ O_T (U). To encrypt it, we form e_m + (xye_m - e_m) - (xe_m - ye_mmodn) ϵ e_m + U to obtain the ciphertext unit

^c = ^yenf modn.

(4)  Decryption procedure: Compute NRTG^m-modn) = em^modn = em.

It is easy to see that this is the Gröbner basis version of the RSA cryptographic primitive studied in Section 7.5. If an attacker is able to factor n, he can break the system. This is equivalent to being able to find d. In the Gröbner basis version, the problem the attacker faces is that he does not know the Gröbner basis elements ye, - e,d_modn.

Also discrete logarithms can be used in Gröbner basis cryptosystems.

Example 14.4.6. Let K = Z₂, let X = {x|, and let M = (X> s N. Then K[M] = K[x] is the univariate polynomial ring over K. Moreover, let p » 0bea prime number. We use the K[x]-module F_2p_₂ = ©f₌_₁¹ K[x]e, ® ©^p_₁¹ K[x]e_;- where e,-, ej are the standard basis vectors. Let g be a generator of the multiplicative group Z*, and let T = deg-pos with e,- >_T ej for all i, j = 1,…,p - 1. Choose a number a ϵ {1,…,p - 1| and compute b = g^amod p. Now we introduce the following Gröbner basis cryptosystem.

(1)  Public information: The module F_2p_₂, i.e., the primep, the set O_T(U) = {e₁, e₂, …, e_p_₁|, the number b, and the vectors {u₁,…, u_s| = {e₁ - e₁| u {xe, - | i = 1,…, p -1 |u {xe_;- - e_bj | j = 1,…, p -11 where all indices are computed modulo p.

(2)  Secret key: The number a ϵ {1,…,p - 1|, or equivalently, the T-Gröbner basis G = {u₁,…, u_s|u - e_ja | i = 1,…,p - 1| of U = (G>.

(3)  Encryption procedure: A plaintext unit is of the form e₁ + e_m with a number m ϵ {0,…,p - 1|. Using the variant, we randomly choose a number k ϵ {0,…,p - 1|, form (e₁ + e_m)x^k and send the ciphertext unit c = + e_mbk ϵ x^k(e₁ + e_m) + sup>(u¹,…^,us>.

(4)  Decryption procedure: We compute NR_{T G}(c) = e_bk + e_mbk. Since e_bk + e_mbk reduces via G to x^k(e₁ + e_m), we have to “divide” this vector by x^k .To this end, it suffices to compute m = (mb^k)/(b^k) in K and to form e₁ + e_m.

Clearly, this is the Gröbner basis version of the ElGamal Cryptosystem of Section 8.1. It can be broken if the attacker is able to compute the discrete logarithm a of b = g^a or k of g^k. In the Gröbner basis version, an attacker can only reduce using e_gt via U¡ to x^ke_x and then via u₁ to x^ke₁. This takes k » 0 reduction steps. If one knows a, one can get rid of the vector e_gt by using just one reduction step e_gt —> e_gka = e_bk.

The next example is based on non-commutative polynomials. In order to prevent linear algebra attacks, T. Rai suggested in his doctoral thesis [Rai] to construct Gröbner basis cryptosystems utilizing two-sided ideals in K(X).

Example 14.4.7. Let K be a (finite) field, let X = {x₁ ,…,x_n}, and let M = (X). Then K[M] = K(X) is the non-commutative polynomial ring. We choose a two-sided ideal

I c K[M] for which we know a finite (two-sided) Gröbner basis G = {g_1;… ,g_t} with respect to some word ordering T .

(1)  Public information: The ring K[M], the set O_T (U), and a finite subset {u₁,…, u_s} ϵ I such that computing a Gröbner basis of (u₁,…, u_s) is infeasible.

(2)  Secret key: The T -Gröbner basis G of I.

(3)  Encryption procedure: A plaintext unit m is an element in (O_T (U))_K. The corresponding ciphertext is c = m + f₁ u₁g₁ + … + f_su_sg_s where the non-commutative polynomials f_i, g_i are suitably chosen so that in the computation of c many leading term cancellations occur (see [Rai], Section 4.1).

(4)  Decryption procedure: Compute m = NR_{T G}(c) using the Gröbner basis G.

In [Rai] several concrete instances of this cryptosystem are proposed. They offer good resistence to linear algebra attacks because using indeterminate coefficients for the polynomials f_i and g_j leads to systems of quadratic equations in these coefficients which cannot be solved using linear algebra. However, one has to take great care to make these instances secure against attackers who are able to compute partial Gröbner bases (see [Rai], Chapter 4).

Our approach also includes the group based cryptosystems studied in Chapter 11. The following Gröbner basis cryptosystem relies on the difficulty of solving the conjugator search problem in certain groups.

Example 14.4.8. Let K be a field, and let M = (x₁,…,x_n; r₁ = … = r_m = 1) beafinitely presented group. We use the free two-sided K[M]-module F_r = ©_wgM K[M] e_wK[M] ® ©we_M K[M] e_w K[M] (which is possibly of infinite rank). Moreover, let T = llex-pos be such that % >_T e_u for all w, u ϵ M. Choose a, g ϵ M and compute g’ = a^-1ga. Now consider the following Gröbner basis cryptosystem.

(1)  Public information: The module F_r, the elements g, g’ ϵ M,asetB c{b ϵ M; ba = ab}, the set O_T(U) = {e_w; w ϵ M}, andthevectors {u_A; A ϵ A} = {eh - e_h-1_ih | i, h ϵ M} u {e_g - e_g, }u {e_;k - e_k-1j_k | j, k ϵ M}.

(2)  Secret key: The element a ϵ M, or equivalently, the T-Gröbner basis G = {u_A | A ϵ A| u - e_a-1_ia | i ϵ M| of the two-sided submodule U = (G> of F_r.

(3)  Encryption procedure: Randomly choose an element b ϵ B. A plaintext unit m ϵ M is written in the form e_g + e_gi_m, where m = bmb_¹. Then we use the elements u_A to obtain the ciphertext unit c = e_b-1_gb + e_b-1_g,_mb.

(4)  Decryption procedure: Find NRt g(c) = e_ar1g„_a + eb-gbm = eb-1gb + eb-gbm first, where g” = b^-1gb. Then determine m using the equality m = (b^-1g^,b)_¹ • (b^g’bm).

As one can readily check, this is a Gröbner basis version of an ElGamal like cryptosystem based on a group with a “hard” Diffie-Hellman conjugacy problem, i.e., the problem to find a_¹b_¹gba given g, a_¹ga and b_¹gb where a and b commute. One can solve this problem if, given g and g = a_¹ga, one can find a₁, a₂ such that a₁ga₂ = g’ and a₁, a₂ commute with the elements from B. The advantage of knowing the Gröbner basis is that one can pass from e_g to the corresponding e, without going through the reduction steps e_g —> e_gi. The computation of that Gröbner basis is equivalent to finding a.

To perform the encryption step explicitly, one has to perform the following simple computations in the group: Conjugate g’ with b to obtain b_¹g^,b and multiply with the plaintext m. Conjugate g with b to obtain b^-1gb.

If we want to decrypt the ciphertext e_b-1_gb + e_b-1_gt_mb knowing the secret a, an explicit decryption amounts to performing the following: conjugate b_¹gb with a to obtain the Gröbner basis element e_b-1_gb - e_a-1_b-1_gba, reduce c via this element in one step to NRt _G(c) = e_a-1_b-1_gba + e_b-1_a-1_gabm and obtain m by multiplying the inverse of the first index with the second index.

So, all computations performed to encrypt and decrypt are actually computations in the group M.

In Chapter 11 braid groups have been suggested for this kind of cryptosystem. However, we mentioned that there is a polynomial time algorithm to solve the Diffie- Hellman conjugacy problem in braid groups. If one chooses reasonable parameters, this algorithm is not feasible today, but it seems that the braid group based version of this cryptosystem may not be secure in the future.

In the final part of this section we collect some remarks about the security of Gröbner basis cryptosystems.

Remark 14.4.9 (Linear Algebra Attacks). Several types of linear algebra attacks have been proposed which apply to special Gröbner basis cryptosystems.

(1)  The basic type is the attack proposed in the original paper [FK]. In the equation c = m + f₁u₁g₁ + … + f_su_sg_s, the attacker regards the coefficients off,,gj as unknowns and tries to solve the resulting system of equations. In our setup, it is possible to make this attack infeasible:

(a)  In general, the system of equations will be quadratic rather than linear.

(b)  Now suppose that the system of equations is linear in a particular setup. By choosing a large set O_T (U), we can make the plaintext m “similar” to the cyphertext c, so that the resulting linear system of equations involves | O_T (U)| coefficients. By using a module of large rank, we can make the solution of this linear system infeasible. Moreover, since we are working over a monoid or group ring, many products (e^t’ with e£ ϵ Supp(u_;) and t ϵ Supp(f) are going to yield the same term, so that the corresponding coefficients cannot be recovered.

(2)  The “intelligent” linear algebra attack suggested by H. W. Lenstra described in [Bar] is based on the idea that in the equation c = m + f₁u₁g₁ + … + f_su_sg_s one can guess the terms t occurring in the support of u₁,…,u_s if t • Suppf) intersects Supp(u), and that the list of all such terms is not too large. As before, in our approach this attack can be repelled in several ways, for instance by choosing a large set O_T (U), by working over group rings, or by using a free module of large rank. In each case sufficient cancellation happens during the computation of the cyphertext.

Remark 14.4.10 (The Attack Using Characteristic Terms). If a representation c = m + f₁u₁g₁ + … + f_su_sg_s is such that there are terms in c which do not belong to O_T (U) and therefore not to Supp(m), then it is sometimes possible to reveal individual messages by performing suitable linear algebra on the coefficients of c and the elements f_t, gj. In particular, this works if there exist “characteristic terms”, i.e., terms which occur in just one of the elements f_t, gj. By recognizing multiples of these terms in the ciphertext one can then reconstruct a constant message unit. As before, this attack rests on the fact that plaintext units are small, i.e., that O_T (U) is small. Furthermore, if several products t •t’ with t ϵ Supp(u,)and t’ ϵ Suppf) u Supp(gj) contribute to one coefficient of c, this attack becomes infeasible. Thus the defensive measures described above apply.

Remark 14.4.11 (Chosen Ciphertext Attacks). In the proposed cryptosystems the receiver has no method to detect invalid ciphertexts. In addition, since decryption is K-linear, the chosen ciphertext attacks described in [Ko2] are possible. However, by using suitable hash functions the system can be made secure in the following way: The sender appends a suitable random value to his message, computes the hash value of the result, and transmits the ciphertext of the message together with the ciphertext of the random value and the hash value. If the receiver detects an invalid ciphertext, he refuses to decrypt or returns a meaningless or random decryption result.

Altogether, it appears that there are sufficiently many defenses for Gröbner Basis Cryptosystems to the known attacks. In fact, breaking them in general would entail breaking essentially all cryptosystems in practical use today.

14.5 Exercises

14.1  Let X = {x₁,…,x_n}, and let a be a complete ordering relation on (X) which is compatible with multiplication. Prove that the following conditions are equivalent.

(a)  The relation a is a well-ordering, i.e., every non-empty subset of (X) has a minimal element.

(b)  Every descending chain w₁ >_a w₂ >_a … in (X) is eventually stationary.

(c)  For every w ϵ (X), we have w >_a 1.

14.2  Show that the length-lexicographic word ordering llex defined in Example 14.1.4 is indeed a word ordering.

14.3  Let K be a field, let I = (x² - xy) c K (x, y), and let a be a word ordering on (x, y) such that x >_a y. Prove that Lw_a(I) = (xyⁱx | i > 0) (see Example 14.1.10).

14.4  Prove the Non-Commutative Division Algorithm 14.1.13. Proceed as in the proof of the commutative case 13.1.10.

14.5  Let P = Z₂(x₁,…,x₆), let a = llex, and let G = (g₁,…,g₅), where the non-commutative polynomials g_i are defined as in Example 14.1.17. Using Buchberger’s Criterion 14.1.16, prove that G is a a-Gröbner basis of the twosided ideal (G).

14.6  Consider the dihedral group D₃ = (x, y; x³ = y² = (xy)² = 1) and its group ring Z₂[D₃] = Z₂(x,y)/I,whereI = (x³ + 1, y² + 1, (xy)² + 1).

(a)  Show that I has the llex-Gröbner basis G = {y² + 1, yxy + x², yx² + xy, xyx + y, x²y + yx, x³ + 1}.

(b)  Find the shortest word representing the inverse of x²y in D₃.

14.7  Let X = {x₁, …,x_n} and I ϵ {1,…, n}. Show that the ordering elim on (X) defined in Example 14.2.2 is a word ordering and an elimination ordering for L = {x1,…,x_f}.

14.8  Work out the proof of Lemma 14.2.3.

14.9  Consider the infinite dihedral group D_TO = (x, y; y² = (xy)² = 1).

(a)  Using the method of Remark 14.2.7, prove that the element x ϵ D_TO has infinite order.

(b)  Similarly, compute the order of the element yxy in the group D₃ = (x, y; x³ = y² = (xy)² = 1).

14.10 Let G = (x₁,…,x_n;r₁ = … = r_m = 1) be a finitely presented group, let Y = {y₁,…, y_n} be a set of further letters such that y_i represents xr¹, let h₁,…,h_k ϵ (X, Y) be words whose residue classes generate a subgroup H = (h₁,…, h_k) of G, andletS be the subalgebra S = Z₂(h₁ - 1,…,h_k - 1) of Z₂[G]. Prove that, for a word w ϵ (X, Y), the following conditions are equivalent.

(a)  w ϵ H

(b)  w - 1 ϵ S

14.11 Consider the free Q(x, y)-module F₂ of rank 2 and the module term ordering T = Pos-llex on T(F₂).Let M bethe Q(x, y)-submodule of F₂ generated by g₁ = x₂x₁e₁x₂ + e₂ and g₂ = e_xx + x₁e₁. Using Buchberger’s Procedure for Modules 14.3.9, enumerate a T-Gröbner basis of M. Showthat G = {g₁, g₂, x₂x^^-1e₁ + (-1)^ke₂x2^k-5 | k > 3} is a T-Gröbner basis of M.

14.12 Formulate and prove a semi-decision procedure for the submodule membership problem in finitely generated K(X)-submodules of F_r.

14.13 Let K be a field, let X = {x₁,…,x„},andletM = (v₁ ,…,v_s) and N = (u₁,…, u_t ) be two K(X)-submodules of the two-sided free module F_r. Consider the inclusions »₁ : F_r ^ F_2r given by »₁(e,-) = e_i and î₂ : F_r ^ F_2r given by *₂(e_f) = e_r+i. Moreover, let

V = (»1(v,-) + »2(v,-) | i = 1,…, s) + (»2(u_;-) | j = 1,…, t).

Prove that M n N = V n(e₁,…, e_r) and conclude that a system of generators of M n N can be enumerated via Buchberger’s Procedure for Modules.

14.14 Let K be a field. Consider the following special case of the Gröbner basis cryptosystem described in Example 14.4.7.

Secret Key: h = z - c ϵ K(x, y, z) with c ϵ K.

Public Information: f = x - a, g = y - b, u₁ = fhg + gh, and u₂ = ghf + hg

in K (x, y, z) with a, b ϵ K.

Show that this instance is not secure, because the secret key can be derived from the public information.

14.15 Let K be a field. Consider the following special case of the Gröbner basis cryptosystem described in Example 14.4.7.

Secret Key: f₁ = z - a, f₂ = w - b in K(x, y, z, w) with a, b ϵ K.

Public Information: u₁ = xf₁y + xf₂y + yf₁ + yf₂ + f₁ + f₂ and u₂ = yf₁x + yf2x + Ay + f2y + A + A.

Show that the secret key cannot be read off the public information. Then explain how this instance can be broken by computing a partial Gröbner basis of U = (u1, u2).

14.16 Let K be a field. Consider the following special case of the Gröbner basis cryptosystem described in Example 14.4.7. In K(x₁, …,x₆), consider the words w₁ = x₁x₃x₅x₄x₂x₆, w₂ = x₁ x₅x₂x₄x₃x₆, and w₃ = x₁x₂x₃x₄x₅x₆.

Secret Key: h = w₃ + c₁x₁ + … + c₆x₆ + c₀, where c₀,…, c₆ ϵ K {0} are arbitrary constants.

Public Information: f = w₁ + a₁x₁ + … + a₆x₆ + a₀ g = w₂ + b₁x₁ + … + b₆x₆ + b₀, where a₁, bj ϵ K {0} are arbitrary constants, u₁ = fhg + gh, and u2 = ghf + hg.

(a)  Prove that the private key can be deduced from the public information as follows: first show that Lw_ff (h) = w₃, Lw_ff(f) = w₁, and Lw_ff(g) = w₂ for a suitable word ordering a. Then find the coefficients c₀,…, c₆ from the coefficients of u₁ and u₂.

(b)  Modify this instance such that the attack described in (a) fails.