3 Cryptanalysis and Complexity

3.1  Cryptanalysis and Cryptanalytic Attacks

As explained in Chapter 1, cryptology has two parts: cryptography and cryptanalysis. Cryptanalysis is the part of cryptology that involves the methods used to break a code or to attempt to break a code. By breaking a code or cryptographic protocol, we mean the ability, under appropriate assumptions, to either determine the secret key or determine the plaintext from the ciphertext without finding the key.

An attempt to break a code is called an attack. The security of a cryptographic protocol depends on its ability to withstand attacks. The person mounting an attack is called an attacker or an eavesdropper. It is common practice to call the communicating parties Bob and Alice and a potential eavesdropper Eve.

An attack usually attempts to take advantage of some weakness in the encryption algorithm that allows one to decode. Cryptanalysis depends also on a knowledge of the form of the code, that is, the type of encryption algorithm employed. Most classical cryptanalysis depends on a statistical frequency analysis of the ciphertext versus the plaintext. An example of a statistical frequency attack is presented in the next section.

First we describe various types of cryptoanalytic attacks. The security of a cryptosystem or general cryptographic protocol depends on its ability to withstand these attacks. In addition, the attack and its chance of success depend upon the security assumptions made. By this we mean the assumptions about what information is available to the eavesdropper or attacker.

(1)  Ciphertext Only Attack: In a ciphertext only attack, an attacker has access to the ciphertext but not the corresponding plaintext. This is the weakest type of attack. A not very efficient method, but one that can always be attempted, is an exhaustive search. The assumption is that the attacker knows the encryption method but needs the secret key. To find the secret key the attacker makes an exhaustive search of the key space. Hence for cryptographic security, the keyspaces in encryption protocols must be large enough so that it is computationally infeasible to do an exhaustive search.
In a ciphertext only attack, if it is known that the encryption is some sort of substitution encryption, then the main method is a statistical attack. This will be examined in the next section.

(2)  Known Plaintext Attack: In a known plaintext attack an attacker has access to some selections of plaintext and the corresponding ciphertext. A known plaintext attack was actually part of the technique used in breaking the Enigma code.

(3)  Chosen Plaintext Attack: In a chosen plaintext attack the attacker has access to a given plaintext and the corresponding ciphertext of his choice. Thus he can determine possible decryptions.

(4)  Chosen Ciphertext Attack: In a chosen ciphertext attack the attacker can decrypt parts of the ciphertext but does not know the whole decryption key.

All of these methods of attack depend upon looking at some portion of an encoded message. There are other attacks that do not depend on looking at encrypted messages at all. These are called side channel attacks. For example, by looking at how much computer time or energy is expended in sending a coded message, an attacker might determine the relative size of the encryption key. In these notes we will not touch on side channel attacks.

In assessing cryptographic security we must also consider whether we have a possible passive attacker or a possible active attacker. A passive attacker can only look at encrypted transmissions but cannot interfere or change them at all. On the other hand, an active attacker has the ability to perhaps modify encrypted transmissions. A very powerful technique along these lines is called the man in the middle attack. Suppose Bob wants to communicate with Alice. The attacker gets in the middle and intercepts Bob’s message. He then alters it in such a way that he can see how it is to be encrypted. He then sends it on to Alice. For example, suppose that Bob wants to get into a bank account and has a password. The attacker gets in the middle and intercepts the password. The attacker then sends the password on to the bank so that Bob does not realize that his password has been stolen. Later, the attacker uses the stolen password to access Bob’s account.

3.2  Statistical Methods

The most common type of attack, and the weakest type of attack, is a ciphertext only attack. Here the attacker has access only to the ciphertext and not any of the plaintext that it came from. The attacker assumes that the encryption is some sort of substitution encryption. Under this assumption, the main method of cryptanalysis is a statistical frequency attack.

A statistical frequency attack on a given cryptosystem requires knowledge, within a given language, of the statistical frequency of k-strings of letters where k is the size of the message unit. In general if k > 1 this is more difficult to determine than the statistical frequency of single letters. As for a letter to letter affine cipher, if k +1 message units, where k is the message block length, are discovered, then the code can be broken (see Chapter 1).

Example 3.2.1. The following table gives the approximate statistical frequency of occurrence of letters in the English language. The passage below is encrypted with a simple permutation cipher without punctuation. we will use a frequency analysis to decode it.

GTJYRIKTHYLJZAFZRLHDHTN

HDNHAGZVDGVHAHFGZVDGVZR

TVMOVFUVHEOMJZDUHRLVUHRZKA

GZUYHRVTAGZVDGVHDNVDKZDVVTZNK

GTJYRIKTHYLZARLVAGZVDGVIS

NVEEMIYZDKAVGTVRGINVAGTJYRHD

HMJAZAZARLVAGZVDGVISFTVHCZDK

ISFTVHCZDKGTJYRIAJARVUARLV

BLIMVAPFWVGRZAZAGHMMVNGTJYRIMIKJ

We first make a frequency analysis letter by letter. We obtain the following data:

This would indicate that V = e and {H, R, A, Z} = {a, t, o, i}. Playing then with the message and trying various permutations of letters with frequency values close to the total frequency values as above we finally arrive at a decoding.

so that the message is.

CRYPTOGRAPHY IS BOTH AN ART AND A SCIENCE. AS A SCIENCE IT RELIES HEAVILY ON MATHEMATICS, COMPUTER SCIENCE AND ENGINEERING. CRYPTOGRAPHY IS THE SCIENCE OF DEVELOPING SECRET CODES. CRYPTANALYSIS IS THE SCIENCE OF BREAKING CRYPTOSYSTEMS. THE WHOLE SUBJECT IS CALLED CRYPTOLOGY.

3.3  Cryptographic Security

The security of a cryptographic protocol is its ability to withstand attacks under given computing and theoretical security assumptions. In reality there are two types of cryptographic security; theoretical security and practical security. Practical security is also called computational security and relies on the computational infeasibility of breaking a cryptographic protocol given security assumptions on the attack. By security assumptions we mean several things.

(1)  What type of cryptographic protocol are we using, and, what is the practical difficulty of the “hard” problem that the protocol is based upon?

(2)  What is the goal of the attacker - for example to break the code completely or recover the secret key or just disrupt transmission?

(3)  What computational power does the attacker have?

On the other hand, theoretical security or information-theoretic security is based on the impossibility of breaking the protocol, even assuming infinite computing power. While theoretical security is stronger than computational security, in most cases it is less practical. Generally, except for the one-time pad that we will discuss in Section 3.4, there are no cryptosystems with perfect security. Hence when we speak of cryptographic security we are speaking of computational security.

3.3.1  Security Proofs

There is no known computational problem that has been proved to be computationally difficult for a reasonable model of computation. Therefore, cryptographic security is generally reduced to tying the feasibility of breaking the protocol to the solvability of a known “hard” problem such as the halting problem for a Turing machine. These hard problems can either be proved to be intractable, or shown to be difficult, in a complexity sense. We discuss a bit of complexity theory in Section 3.7.

A security proof, or security reduction, for a cryptographic protocol is a proof that shows that breaking the protocol is equivalent to, or dependent upon, solving some known difficult problem. Hence if P is a difficult problem, and ε denotes some protocol, then a security proof for ε is a proof that says that breaking the encryption method ε implies a solution to the problem P. Therefore cryptographic security proofs are relative.

The most common public key protocols, Diffie-Hellman and RSA, do not have any true security proofs, since the difficulty of the problems that they depend upon is not really known. The Diffie-Hellman protocol, that we will introduce in Chapter 5, is dependent upon the discrete log problem that we briefly discussed in Chapter 2. There are no known efficient algorithms to solve this problem but its theoretical difficulty is unknown. What is known is that the protocol has not be broken in the forty years since its introduction. Similarly the RSA protocol is based on the difficulty of factoring large integers. Again there is no security proof but no efficient algorithm has been developed to break the whole system.

In Chapter 5 we will examine various algorithms to attempt to solve both the discrete log problem and the factorization problem. These algorithms then become potential attacks on the Diffie-Hellman and RSA protocols whose security depends on the difficulty of solving these problems.

3.4  Perfect Security and the One-Time Pad

Claude Shannon, in a famous paper in 1949 (see [Sha3]), placed a mathematical model on cryptographic security in terms of probability. In his mathematical model, Shannon introduced the concept of placing a probability distribution on the set of plaintext message units, on the set of keys, and on the set of ciphertext message units. From these probability distributions, he defined both perfect security or perfect secrecy and what it means in a mathematical sense to break a code.

In general an encryption protocol has perfect security if an observer learns nothing about a plaintext message (expect possibly its maximal length) by observing the corresponding cipher text. To place this in a mathematical context, we let P denote the set of plaintext messages, C the set of ciphertext messages, and K the set of keys. We assume that there are probability distributions on all three sets. We refer to [Fre] for any information on probability theory.

Definition 3.4.1. Let P be the set of plaintext messages, C the set of ciphertext messages and K the set of keys for a cryptographic protocol ε. Then ε has perfect security if for any given plaintext message P and corresponding ciphertext message C we have Prob(P|C) = Prob(P), that is, the conditional probability of determining the plaintext message P, given knowledge of the ciphertext message C, is exactly the same as the absolute probability of determining the plaintext P.

Shannon then proved the following strong theorem, that describes when a cryptographic protocol is perfectly secure.

Theorem 3.4.2. Let P be the set of plaintext messages, C the set of ciphertext messages and K the set of keys for a cryptographic protocol E. We assume that all three sets have probability distributions on them. Suppose that the sets P, C and K are all infinite and Prob(P) > 0 for any plaintext P. Then E has perfect security if and only if the key space is uniformly distributed and if for any plaintext P and any ciphertext C there is exactly one key k that encrypts P by C.

From this definition, Shannon proved that the one-time pad, that we describe shortly, has perfect security.

Perfect security is difficult to obtain. Closely related is semantic security. This is the appropriate notion of security relative to a passive attacker. A cryptosystem is semantically secure relative to given security assumptions if it is infeasible for a passive attacker to determine relevant information about a plaintext given an observation of a ciphertext.

The one type of cryptographic protocol that has been proved to be perfectly secure is the one-time pad or Vernam one-time pad. This was developed for telegraphic security in the nineteenth century but was patented by Gilbert Vernam in 1917. In the paper of Shannon, mentioned above, it was proved that this method has perfect security. In a one-time pad the plaintext are sequences of bits of a given length and the ciphertext is the plaintext XOR’ed with a single time use key given also by a sequence of bits of the same length as the plaintext. Formally:

Definition 3.4.3. Suppose the sets P of plaintext messages, C of ciphertext messages and K of keys are all given by elements of {0,1}”. That is, plaintext messages, ciphertext messages and keys are all random bit strings of fixed length n. For a given key k ∈ K the encryption function is given by F_k(p) = p ⊕ k for p ∈ P. We assume that the distribution on all three sets is the uniform distribution and a key k is only used once. The resulting encryption protocol is called a one-time pad or Vernam one-time pad.

Shannon proved that the one-time pad, under the assumptions provided in the definition, is perfectly secure, as long as the keys are randomly chosen and used only once.

Theorem 3.4.4 (Shannon). A one-time keypad has perfectsecrecy if the keys are randomly chosen from the uniform distribution of keys and a key is used only once.

Shannon also showed that if a key is used more than once the perfect security is lost. A one-time pad is also not secure against an active attacker who can change, to his advantage, the length of the message.

Although the one-time pad is theoretically secure there are many problems with its practical use.

(1)  The one-time pad requires perfectly secure and random keys. Hence,to be able to to use it we need a secure method to generate random bits. Theoretically, if pseudo-random numbers are used the perfect security falls by the wayside.

(2)  For the one-time pad, there must be secure generation and secure transmission of the keys which must be as long as the plaintext.

(3)  A key can be used only once.

For these reasons the one-time pad, while important theoretically, is not used to a great extent in encryption. However, stream ciphers, as described in the previous chapter, are a method to attempt to mimic the important properties of the one-time pad. For this reason stream ciphers are often called Vernam ciphers.

3.4.1  Vigènere Encryption and Polyalphabetic Ciphers

Another method to copy the security properties of the one-time pad is the use of polyalphabetic ciphers. By this we mean that a plaintext letter can be encrypted differently in a different place. The first version of a polyalphabetic coding system was given by Alberti in about 1466. This was mentioned in Chapter 1. Such cryptosystems now are called Vigènere cryptosystems after Vigènere who included the method in his book in 1586. The famous Enigma machine was a type of Vigènere cipher.

In the simplest variation of a Vigènere cryptosystem we have the following. We begin with an N-letter alphabet. This is the plaintext alphabet. We then form an N × N matrix P where each row and column is a distinct permutation of the plaintext alphabet. Hence P is a permutation matrix on the integers 0,..., N - 1. The communicating parties decide on a keyword. This is private between the communicators. To encrypt the keyword is placed above the plaintext message over and over until each plaintext letter lies below a letter in the keyword. The ciphertext letter corresponding to a given plaintext letter is determined by the alphabet at the intersection of the keyword letter and plaintext letter below it.

To clarify this description, and make Vigènere encryption precise, we repeat the example given in Chapter 1. Here we suppose that we have a 9 letter plaintext alphabet A, B, C, D, E, O, S, T, U. For simplicity in this example we will assume that each row is just a shift of the previous row, but any permutation can be used. We then have the following collection of alphabets.

Suppose that Bob and Alice are the communicating parties and they have chosen the keyword BET. This is held in secret by the two of them. Suppose that the plaintext message to be encrypted is STAB DOC. The keyword BET is placed repeatedly over the message until the plaintext message if filled as below.

To encrypt we look at B which lies over S The next key letter. The intersection of the B key letter and the S alphabet is a t so we encrypt the S with T. The next key letter is E which lies over T. The intersection of the ε keyletter with the T alphabet is c. Continuing in this manner and ignoring the space we get the encryption

STAB DOC → TCTCTDD

To descrypt we use the keyword BET but now use the method over the cipher text TCTCTDD.

For a long period of time polyalphabetic ciphers were considered unbreakable. In the mid nineteenth century Kasiski developed a technique for the cryptanalysis of Vigènere cryptosystems. Since then there has been substantial work done on the cryptanalysis of Vigènere ciphers. We will describe two of these techniques.

In 1863 the Kasiski test was developed. With this method one can try to determine the length of the key word. If the same partial word appears in the plaintext occurs several times then in general it will be encrypted differently. However, if the distance between the first letter of the respective partial word is a multiple of the key word length then the partial word will be encrypted the same. We have to look for partial sequences of length ≥ 3 in the cipher text. There respective distances are probably divisible by the length of the key word.

Then we determine the greatest common divisor as often as possible of such distances. If these are for example 14, 27,21,35,..., then the key word length could be 7.

We now can try to find the key word as follows. The keyword k is represented by a tuple (n₁,..., n_t) where we found the keyword length t. Then form the sets:

Now carry out a frequency analysis for the sets M₁, M₂,...,M_t and get possible values for n₁,...,n_t of the keyword.

In 1920, a second test, the Friedmann test was further developed. We assume that N =26 and the alphabet is {A, B, C,...| but the method is entirely general. Let (a_n,..., a_n) bea sequence oflength n of letters from the alphabet. Let n₁ be the number of A's that occur, n₂ the number of B's and so on. Then:

(a)  There are pairs of A’s in the sequence, pairs of B’s and so on.

(b)  There are altogether pairs of equal letters.

(c)  The probability that two randomly chosen letters are equal is therefore given by

This number is called the Friedmann Coincidence Index.

For German texts the empirically established value for sequences of letters gives p_F ≈ 0.0762

Theorem 3.4.5. Given a sequence of letters of length m representing a Vigènere encrypted cipher text and let p_F be its Friedman Coincidence Index. Let p_L be the Friedmann Coincidence Index representing the corresponding plaintext (which is unknown but, for example, is usually taken as p_L = 0.0762 for German texts). Then the length t of the keyword is

Proof. We assume approximately that t divides m where m is the length of the sequence (a₁..., a_m) representing the cipher reset. We write (a₁..., a_m) in t columns

Each column is encrypted with a single alphabet (or a Caesar cipher). We have always the same shift cipher. Hence the coincidence index is about p_L (each column is a shifted plain text). The probability that two letters from different columns are equal is about .

Each column has m letters. The number of pairs of letters, which are in the same column, is

The number of pairs of letters that are in different columns is

Hence altogether the number K of pairs of equal letters is

Hence

If we solve this for t we get the result

3.4.2  Breaking a Protocol

We have defined the general concept of security and defined perfect security, but what exactly is the mathematical formulation of breaking a code? This is formally defined in terms of encrypted bits. Let ε = 0,1 be an encrypted bit. In the absence of any information, the determination of e is entirely random, and hence, the probability of correctly determining ε is . Given a set of security assumptions, then a cryptosystem is said to be broken, and an attack successful,if by using the attack, the probability of correctly determining an encrypted bit is greater than , within a feasible time frame of the encryption. We make this precise.

Definition 3.4.6. Let S be a set of security assumptions for a cryptographic protocol, A a given attack, B the event of correctly determining an encrypted bit from the protocol and finally T a feasible time frame relative to the encryption. Then the attack A is successful and the protocol broken if

Notice that a cryptosystem may be broken but messages may still be relatively secure since the definition is given solely in terms of encrypted bits. It may still be difficult to then correctly determine a given message. Of course the greater the probability in the previous definition the greater the probability of decrypting the entire message.

A probability, marginally greater than 1 may have a low probability of total message recovery. For example, suppose that and the decryption of bits is independent. To then correctly decrypt n bits the probability if (. 56)” which of course can be very small. However, given a set of correct bits the message may be decrypted directly by knowing the gist of the message.

3.5  Complexity of Algorithms: Generic and Average Case

As we have seen, an extremely important aspect of any cryptosystem is its security, that is how well the encryption algorithm withstands various type of attacks. Theoretically this involves the complexity of the encryption algorithm. Generally an encryption algorithm is based upon some hard to solve problem. In classical cryptography these problems were either number theoretic or combinatorial, however, in group based cryptography the security can be based on group theoretical problems. In practice a problem should be hard to solve both theoretically and practically, like the discrete log problem, to be a valid problem for use in cryptography. Using a hard to solve problem in cryptography involves constructing a trapdoor function whose inverse depends upon the solution to the problem. This trapdoor function would be based on a secret key which makes the hard to solve problem solvable.

Determining how difficult a problem is to solve involves some important aspects of theoretical computer science and in particular complexity theory. In this section we go over some basic concepts.

First we describe a method to compare functions.

Suppose that f (x),g(x) are positive real valued functions. Then

(1)  f(x) = O(g(x)) (This is read as f(x) is big O of g(x).) if there exists a constant A independent of x and an x₀ such that

f (x) ≤ Ag(x) forall x ≥ x₀.

(2)  f (x) = o(g(x)) (This is read as f (x) is little o of g(x).) if

In other words g(x) is of a higher order of magnitude than f (x).

(3)  If f(x) = O(g(x)) and g(x) = Of (x)), that is there exist constants A₁, A₂ independent of x and an x₀ such that

then we say that f (x) and g(x) are of the same order of magnitude and write

(4)  If

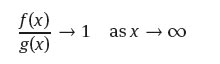
then we say that f (x) and g(x) are asymptotically equal and we write

In general we write O(g) or o(g) to signify an unspecified function f such that f = O(g) or f = o(g). Hence for example, writing f = g + o(x) means that and saying that f is o(1) means that

It is clear that being o(g) implies being O(g) but not necessarily the other way around. Further it is easy to see that

The length of an integer is its total number of binary bits. An algorithm is a polynomial time algorithm if there exists an integer d such that the number of bit operations required to perform the algorithm on integers of total length k is O(k^d). The ordinary arithmetic operations, for example, are polynomial time algorithms. An exponential time algorithm has a time estimate of O(e^ck) on integer inputs of total length k. Factoring an integer or primality testing an integer by trial division is an exponential time algorithm.

Definition 3.5.1. A decision problem P is a polynomial time problem if there exists a constant c and an algorithm such that if an instance of P has length ≤ n then the algorithm answers the problem in time O(n^c). We denote the class of polynomial time problems by P.

Definition 3.5.2. A decision problem is in non-deterministic polynomial time if a person with unlimited computing power not only can answer the problem but if the answer is “yes” the solver can supply evidence that another person could use to verify the correctness of the answer in polynomial time. The demonstration that the “yes” answer is correct is called a polynomial time certificate. The class of non-deterministic polynomial time problems is denoted by NP.

The class co-NP consists of problems like those in NP but with “yes” replaced by “no”.

If a problem can be solved in polynomial time it can certainly be solved in non- deterministic polynomial time. Therefore P ⊂ NP,thatisthe classofproblemssolvable in polynomial time is a subset of the class of problems solvable in non-deterministic polynomial time. However, no example has been found of a problem solvable in non- deterministic polynomial time that cannot be solved in polynomial time. Therefore it has not been proved that P ≠ NP. The P = NP question is the most important open problem now in computer science.

If P₁ and P₂ are two decision problems then we say that P₁ reduces to P₂ in polynomial time if there exists a polynomial time algorithm that constructs an answer for P₂ given a solution to Pj. Hence the problem of breaking the ElGamal cryptosystem reduces to the discrete log problem (see next chapter).

Finally a decision problem is NP-complete if any other problem in NP can be reduced to it in polynomial time. A decision problem is NP-hard if any NP problem reduces to it.

A good cryptographic decision problem should be at least NP-hard. However, what is also important is average case complexity as opposed to worst case complexity.

The worst case complexity of a problem is the hardest instance of the problem. Hence an algorithm to solve a problem has exponential worst case complexity if there exists an instance of the problem which is exponential to solve with that algorithm. The average case complexity of an algorithm is the complexity on average of the algorithm where a measure is put on the set of inputs. Finally an algorithm has generic case complexity if given a measure on the set of inputs the algorithm solves the problem with measure one.

A more complete discussion of the various complexity classes and the interrelationship between them can be found in the book [MSU1].

3.6  Exercises

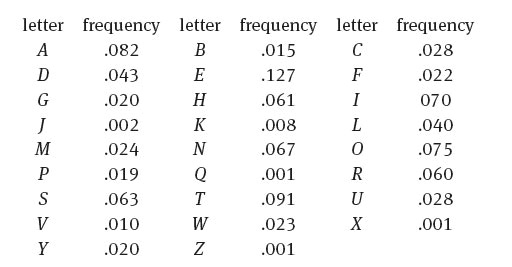
3.1    The table below gives the approximate statistical frequency of occurrence of letters in the English language. The following passage is encrypted with a simple substitution cipher without punctuation. Use a frequency analysis to decode it.

3.2    A text of Edgar Allen Poe from the “The Gold-Bug” is encrypted with the Vi- genere cryptosystem using the keyword gold. The ciphertext is

Use a frequency analysis to decode the ciphertext.

3.3    Using an encryption with a Vigènere cryptosystem we obtained the ciphertest

Calculate the key length k with the help of the Kasiski test and the Friedmann test.

3.4    Use the Vigènere code to encode the German sentence

In Hamburg an der Alster traf ich einen ehemaligen Schulkameraden und wir plauderten von alten Zeiten.

with help of the keyword Schule.

3.5    The following message is in ciphertext encoding a German language plaintext message. The last ten digits have been lost and don’t appear on the list below. What are the missing digits and which cryptosystem was used?

3.6    The following message has been encrypted with the Vernam one-time pad. The ciphertext is:

What is the plaintext?

3.7    The plaintext 010101 is encrypted with a Vernam one-time pad to the ciphertext 101010. What is the key?

(a)  000000

(b)  111111

(c)  000111

3.8    Let m be the number of bit operations required to compute 3ⁿ in binary. Estimate using the big-O notation m as a simple function of n, the input binary digits.

(a)  Do the same for nⁿ.

(b)  Estimate in terms of a simple function of n and N the number of bit operations required to compute Nⁿ.

3.9    Consider the ciphertext message

The following is known about the cryptosystem that constructed this code.

(1)  A Vigènere cryptosystem was used with a pseudo random k.

(2)  The key was generated with a 4-bit LFSR with elements from Z₂₆ in the cells.

(3)  A probable word in the plaintext is BROADCAST.

(a)  Decrypt the message.

(b)  Encrypt the rest of the text announced the Allied invasion to be expected within forty-eight hours.

(c)  Calculate the period of this LFSR.