1.1 Mathematical Cryptography
The subject of this book is mathematical cryptography. By this we mean the mathematics involved in cryptographic protocols. We will define, and make precise, all these terms as we proceed. As the field has expanded, using both commutative and non-commutative algebraic objects as cryptographic platforms, we felt that a book describing and explaining all these mathematical methods would be of considerable value.
Cryptography or cryptology is loosely the science of encrypting and decrypting secret codes, and the related task of breaking or uncovering secret codes. The science of cryptography touches on many other disciplines, both within mathematics and computer science and in engineering. In mathematics, cryptology uses, and touches on, algebra, number theory, graph and lattice theory, algebraic geometry and probability and statistics. Analysis of cryptographic security leads to using theoretical computer science especially complexity theory. The actual implementation of cryptosystems, and the hard work of carrying out security analysis for specific cryptosystems falls into engineering and practical computer science and computing. In this book we will look primarily at the first part, the mathematics of cryptographic protocols. We will not look at all at hardware implementation. In Section 1.2 we will present many of the terms and mathematical formulations in cryptology. Section 1.2 will be further expanded in Chapter 2.
Up until fairly recently, cryptography was mainly concerned with message confidentiality - that is sending secret messages so that interceptors or eavesdroppers cannot decipher them. The discipline was primarily used in military and espionage situations and as recently as the 1956 Encyclopedia Brittanica article on Cryptography said that there seemed to be only limited use in business and commerce. Two things changed all that. The first was the increased capability and use of computers and computing. This both allowed more complex encryption systems that could not be done by hand but could be on a computer, and required more complex encryption, since cryptanalysis, that is, code breaking, was enhanced by the computer. The second thing that skyrocketed the use of cryptographic methods was the discovery of workable one way functions that then allowed for public key cryptosystems. This allowed the transmission of sensitive data over public airwaves even though any potential attacker could view this data and further the attacker knew the encryption technique. In Section 1.3 we give a very brief history of cryptography while in Section 1.5 and then again in Chapter 2 we describe the basic ideas differentiating classical or symmetric key cryptography from public key cryptography.
An important aspect of cryptographic protocols are their security, that is the ability of the encryption to withstand attacks from unwanted adversaries. Since modern cryptography is done on a computer, cryptographic security must bring in ideas from computer science and complexity theory. We will present some of these ideas from a mathematical viewpoint in Chapter 3. The book [MSU1] by Myasnikov, Shpilrain and Ushakov provides a much more extensive discussion of complexity theory and its relationship and use relative to cryptography.
Traditionally, the main mathematical tools involved in cryptographic protocols were number theoretic. To encrypt an alphabet with N letters the letters were considered as modular integers 0,1, 2,N - 1 in the modular ring 
N. Number theoretic functions on N were then used. The main public key cryptographic methods, Diffie- Hellman and RSA, are based on supposedly hard number theoretic problems, the discrete logarithm problem and the factorization problem respectively. We touch on these ideas in Section 1.4 and then much more fully in Chapter 6. We will discuss the main traditional public key methods in Chapter 7. In an attempt to build cryptosystems with smaller necessary key spaces, algebraic geometry was introduced to cryptography. The concepts of elliptic curves and their corresponding elliptic curve groups were combined with the Diffie-Hellman concepts to build elliptic curve cryptography. We discuss elliptic curve methods in Chapter 8.
The traditional cryptographic methods, both symmetric key and public key, such as the RSA algorithm, Diffie-Hellman, and elliptic curve methods, are number theory based. Hence, from a theoretical point of view, they depend on the structure of abelian groups. Although there have been no successful attacks on the standard protocols, there is a feeling that the strength of computing machinery has made these techniques less secure. The big cloud in this direction are quantum algorithms and the possibility that a workable quantum computer can be built. Quantum algorithms can break the present versions of both Diffie-Hellman and RSA. We will briefly touch on quantum algorithms in Chapter 3.
As a result of this, there has been an active line of research to develop and analyze new cryptosystems and key exchange protocols based on non-commutative cryptographic platforms. This line of investigation has been given the broad title of noncommutative algebraic cryptography.
Up to this point the main sources for non-commutative cryptographic platforms have been non-abelian groups. In cryptosystems based on these objects, algebraic properties of the platforms are used prominently in both devising cryptosystems and in cryptanalysis. In particular the difficulty, in a complexity sense, of certain algorithmic problems in finitely presented groups, such as the conjugator search problem, has been crucial in encryption and decryption. We give an introduction to these group theoretic ideas in Chapters 9 and 10. Chapter 11 deals with the main public key methods using non-abelian groups, the Ko-Lee method and the Anshel-Anshel-Goldfeld method.
The main sources for non-abelian groups are combinatorial group theory and linear group theory. Braid group cryptography, where encryption is done within the classical braid groups, is one prominent example. The one-way functions in braid group systems are based on the difficulty of solving group theoretic decision problems such as the conjugacy problem and conjugator search problem. Although braid group cryptography had initially a lot of success, various potential attacks have been identified. Besides discussing braid groups and braid group cryptography, Chapter 11 introduces what is necessary for a general non-abelian cryptographic protocol. The study and cryptanalysis of potential platform groups has had a strong positive effect on both group theory and complexity theory. Motivated in large part by cryptography, there has been tremendous interest in asymptotic group theory and generic properties. We discuss these in several places in this book.
Chapter 12 describes further uses of non-abelian groups in cryptography. One idea that we will describe is to replace the social security number by a finitely presented group and then encode a persons’ information securely within that group.
Gröbner bases have also been employed both to develop non-commutative cryptosystems and to cryptanalyze other systems that are polynomial based. Chapters 13 and 14 describe these Gröbner basis techniques.
The use of lattices as cryptographic platforms has also generated a generated a great deal of interest, primarily because these methods seem to be resistant to attacks by quantum algorithms. We provide an overview of lattice based cryptography in Chapter 15.
1.2 Cryptography, Cryptanalysis and Cryptosystems
In this section we start to introduce the basic terminology and mathematics used in cryptography. In later sections we will make these ideas more precise.
Cryptography refers to the science and/or art of sending and receiving coded messages. Coding and hidden ciphering is an old endeavor used by governments and militaries and between private individuals from ancient times. Recently it has become even more prominent because of the necessity of sending secure and private information, such as credit card numbers, over essentially open communication systems.
Traditionally cryptography is the science of devising and implementing secret codes or cryptosystems. Cryptanalysis is the science of breaking cryptosystems while cryptology refers to the whole field of cryptography plus cryptanalysis. In most modern literature cryptography is used synonymously with cryptology. Theoretically cryptography uses mathematics, computer science and engineering.
A cryptosystem or code is an algorithm to change a plain message, called the plaintext message, into a coded message, called the ciphertext message. In general both the plaintext message (uncoded message) and the ciphertext message (coded message) are written in some N-letter alphabet which is usually the same for both plaintext and code. The method of coding, or the encoding algorithm, is then a transformation of the N-letters. The most common way to perform this transformation is to consider the N letters as N integers modulo N and then perform a number theoretical function on them. Therefore most encoding algorithms use modular arithmetic and hence cryptography is closely tied to number theory. In this section we give a brief overview of cryptography and some number theoretic algorithms used in encryption. The subject is very broad, and as mentioned above, very current, due to the need for publicly viewed but coded messages. There are many references to the subject. The book by Koblitz [Ko1] gives an outstanding introduction to the interaction between number theory and cryptography. It also includes many references to other sources. The books by Buchmann [Buc] and Stinson [Sti2] describe the whole area.
Modern cryptography is usually separated into classical cryptography, also called symmetric key cryptography, and public key cryptography. In the former, both the encoding and decoding algorithms are supposedly known only to the sender and receiver, usually referred to as Bob and Alice. In the latter, the encryption method is public knowledge but only the receiver knows how to decode. We make this more precise in Chapter 6 when we discuss public key methods in detail. Here we present first the basic terminology used in classical cryptography.
The message that one wants to send is written in plaintext and then converted into code. The coded message is written in ciphertext. The plaintext message and ciphertext message are written in some alphabets that are usually the same. The process of putting the plaintext message into code is called enciphering or encryption while the reverse process is called deciphering or decryption. Encryption algorithms break the plaintext and ciphertext message into message units. These are single letters or pairs of letters or more generally fc-vectors of letters. The transformations are done on these message units and the encryption algorithm is a mapping from the set of plaintext message units to the set of ciphertext message units. Putting this into a mathematical formulation we let
The encryption algorithm is then the application of an injective map
The map f is the encryption map. The left inverse map
is the decryption or deciphering map. The collection 
, consisting of a set of plaintext message units, a set of ciphertext message units, an encryption map and its left inverse is called a basic cryptosystem. Later in this chapter we will present a broader definition of a cryptosystem which also includes an index set called the key space. For the present we will use cryptosystem to mean basic cryptosystem.
Breaking a code is called cryptanalysis. An attempt to break a code is called an attack. Most cryptanalysis depends on a statistical frequency analysis of the plaintext language used (see exercises). Cryptanalysis depends also on a knowledge of the form of the code, that is, the type of cryptosystem used.
We now present some simple examples of cryptosystems and cryptanalysis.
Example 1.2.1. The simplest type of encryption algorithm is a permutation cipher. Here the letters of the plaintext alphabet are permuted and the plaintext message is sent in the permuted letters. Mathematically if the alphabet has N letters and a is a permutation on 1,…, N, the letter i in each message unit is replaced by σ(i). For example suppose the plaintext language is English and the plaintext word is BOB and the permutation algorithm is
Example 1.2.2. A very straightforward example of a permutation encryption algorithm is a shift algorithm. Here we consider the plaintext alphabet as the integers 0 ,1,…, N - 1 (mod N). We choose a fixed integer k and the encryption algorithm is
f (m) = (m + k) (mod N).
This is often known as a Caesar code after Julius Caesar who supposedly invented it. It was used by the Union Army during the American Civil War. For example if both the plaintext and ciphertext alphabets were English and each message unit was a single letter then N =26. Suppose k = 5 and we wish to send the message ATTACK. If a = Othen ATTACK is the numerical sequence 0,19,19,0,2,10. The encoded message would then be FYYFHP.
Any permutation encryption algorithm which goes letter to letter is very simple to attack using a statistical analysis. If enough messages are intercepted and the plaintext language is guessed then a frequency analysis of the letters will suffice to crack the code. For example in the English language the three most commonly occurring letters are E, T and A with a frequency of occurrence of approximately 13 %, 9 % and 8 % respectively. By examining the frequency of occurrences of letters in the ciphertext, the letters corresponding to E, T and A can be uncovered. In the next chapter we present an example of a statistical attack in English.
Polyalphabetic ciphers are an attempt to thwart statistical attacks. In these coding methods, different letters may be encrypted with different alphabets. One variation of the basic Caesar code is the following where message units are fc-vectors. It is actually a type of polyalphabetic cipher called a Vigenére code.
Example 1.2.3. In this code, message units are considered as k-vectors of integers modulo N from an N letter alphabet. Let B = (b1, …,bk) be a fixed k-vector in nk. The Vigenere code then takes a message unit
The vector (b1,…, bk) in the example above is called a key. Another version of a polyalphabetic cipher in given in the next example which further uses the idea of a key needed to unlock the code.
Example 1.2.4. Suppose we have an N-letter alphabet. We then form an N × N matrix P where each row and column is a distinct permutation of the plaintext alphabet. Hence P is a permutation matrix on the integers 0,…, N - 1. Bob and Alice decide on a keyword. The keyword is placed above the plaintext message and the intersection of the keyword letter and plaintext letter below it will determine which cipher alphabet to use. Let us make this precise with a 9 letter alphabet A, B, C, D, E, O, S, T, U. Here for simplicity we assume that each row is just a shift of the previous row, but any permutation can be used.
Key Letters
Suppose the plaintext message is STAB DOC and Bob and Alice have chosen the keyword BET. We place the keyword repeatedly over the message
To encode we look at B which lies over S. The intersection of the B key letter and the S alphabet is a t so we encrypt the S with T. The next key letter is E which lies over T. The intersection of the E key letter with the T alphabet is c. Continuing in this manner and ignoring the space we get the encryption
Example 1.2.5. A final example, which is not number theory based, is the so-called Beale Cipher. This has a very interesting history which is related in the popular book Archimedes Revenge by P. Hoffman (see [Hof]). Here letters are encrypted by numbering the first letters of each word in some document like the Declaration of Independence or the Bible. There will then be several choices for each letter and a Beale cipher is quite difficult to attack.
1.3 A Very Brief History of Cryptography
Until relatively recent times cryptography was mainly concerned with message confidentiality, that is, sending secret messages so that interceptors or eavesdroppers cannot decipher them. The discipline was primarily used in military and espionage situations. As explained in the introduction this changed with the vast amount of confidential data that had to be transmitted over public airways so the field has expanded to may different types of cryptographic techniques such as digital signatures and message authentications.
Cryptography and encryption does have a long and celebrated history. In the Bible, in the book of Jeremiah, they use what is called an Atabash Code. In this the letters of the alphabet, Hebrew in the Bible, but can be used with any alphabet, are permuted first to last. That is, in the Latin alphabet Z would go to A and so on.
The Kabbalists and the Kabbala believe that the Bible - written in Hebrew where each letter also stands for a number- is a code from heaven. They have devised elaborate ways to decode it. This idea has seeped into popular culture where the book “The Bible Code” became a bestseller.
In his military campaigns Julius Caesar would send out coded messages. His method, which we looked at in the last section, is now known as a Caesar code. It is a shift cipher. That is each letter is shifted a certain amount to the right. A shift cipher is a special case of an affine cipher that will be elaborated upon in the next section. The Caesar code was resurrected and used during the American Civil War.
Coded messages produced by most of the historical methods reveal statistical information about the plaintext. This could be used in most cases to break the codes. The discovery of frequency analysis was done by the Arab mathematican Al-Kindi in the ninth century and the basic classical substitution ciphers became more or less easily breakable.
The use of ciphers and code books flourished during the political intrigues in Europe during the middle ages and the use of codes and code books became prevalent in diplomacy. About 1470 Leon Alberti developed a method to attempt to thwart statistical analysis. His innovation was to use a polyalphabetic cipher where different parts of the message are encrypted with different alphabets. His method was mistakenly attributed to the French cryptographer Blaise de Vigenere, who was a century later than Alberti. The type of polylaphabetic code as described in Example 1.2.4 is now referred to as a Vigenere code. Further work was done on polyaphabetic codes by Johannes Trithemius and G. B. Belasso in the sixteenth century. Belasso seems to be the first to describe, in a book, the mechanics of polyalphabetic codes. Vigenere was a mathematician and cryptographer who worked and wrote about on many different types of ciphers. Famous mathematicians, Charles Dodgson (Lewis Carrol of Alice in Wonderland fame)and CharlesBabbage, alsowrote on theVigenerecodeand Babbage actually broke a version of it.
A different way to thwart statistical attacks is to use blanks, that is, meaningless letters within the message. Mary, Queen of Scots, used a random permutation cipher with neutrals in it where a neutral was a random meaningless symbol. Unfortunately for her, her messages were decoded, and she was beheaded.
There have been various physical devices and aids used to create codes. Prior to the widespread use of the computer, the most famous cryptographic aid was the Enigma machine developed and used by the German military during the Second World War. This was a rotor machine using a polyalphabetic cipher. An early version was broken by Polish cryptographers early in the war, so a larger system was built that was considered unbreakable. British cryptographers led by Alan Turing broke this and British knowledge of German secrets had a great effect on the latter part of the war.
The development of digital computers allowed for the development of much more complicated cryptosystems. Further this allowed for the encryption using anything that can be placed in binary formats whereas historical cryptosystems could only be rendered using language texts. This has revolutionized cryptography. The use of computers also required the development of more complex encryption methods since computing capability enhanced the ability to cryptanalyze, that is break cryptosystems.
In 1976 Diffie and Hellman developed the first usable public key exchange protocol. This allowed for the transmission of secret data over open airways. A year later, Rivest, Adelman and Shamir, developed the RSA algorithm a second public key protocol. There are now many and we will discuss them later. In 1997 it became known that public key cryptography had been developed earlier by James Ellis working for British Intelligience and that both the Diffie-Hellman and RSA protocols had been developed earlier by Malcom Williamson and Clifford Cocks respectively.
Both Diffie-Hellman and RSA require very large key spaces (see Chapter 2). In an attempt to use the same ideas but reduce the key space size it was suggested that Diffie-Hellman be applied to other abelian groups. To do this, algebraic geometry was introduced into cryptography. In 1985 Neil Koblitz and independently Victor Miller suggested the use of elliptic curves over finite fields and their corresponding groups as possible cryptographic platforms. These methods have been quite successful and result, in many cases, in faster encryption and smaller key spaces than standard RSA methods.
As cryptographic applications became more prevalent it was felt that there should be an encryption standard. In 1976, the Data Encryption Standard (DES) was adopted as the standard for symmetric key encryption. DES is what is called a block cipher and has the structure of a so-called Feistel network. In Chapter 2 we discuss Feistel networks and DES in detail.
The original DES is now insecure for many applications and there have been successful attacks on it, the first being in 1999. Subsequently a competition was initiated to find a secure replacement. The winner was developed by Rijmen and Daemen and their method is called the Rijndael cipher. This method is also a block cipher that proceeds with several rounds of encrypting blocks and then mixing blocks. In 2001 the National Institute of Standards and Technology of the United States adopted a standardization of the Rijndael cipher, now called AES for Advanced Encryption Standard, as the industry standard for a symmetric key encryption. Although not universally used it is the most widely used. We will discuss AES further in Chapter 2.
Finally within the past twenty years the ideas of quantum algorithms and the possibility of a workable quantum computer led researchers to start to consider public key methods using non-abelian groups. In 1999 Ko, Lee et al. (see [KLCHKP]) and Anshel- Anshel-Goldfeld (see [AAG1]) introduced public key exchange methods involving the braid groups as platforms. There has been an active line of research over the past fifteen years in this area.
This has been a whirlwind look at cryptography’s past. The complete history of cryptography is both extensive and fascinating. The books by David Kahn [Kha] and Simon Singh [Sin] provide a wealth of information.
1.4 Encryption and Number Theory
Most of traditional cryptographic methods are number theory based. At the simplest level these techniques use modular arithmetic, however a wide array of complicated number theory is used in cryptography. In Chapters 4 and 5 we will give a full description of modular arithmetic and its use in cryptography. In this introductory section we describe some elementary number theoretically derived cryptosystems. This is to provide a flavor of how number theory enters cryptography.
In applying a cryptosystem to an N letter alphabet we consider the letters as integers modulo N. The encryption algorithms then apply number theoretic functions and use modular arithmetic on these integers. One example of this was the shift or Caesar cipher described in Example 1.3.2. In this encryption method, a fixed integer k is chosen and the encryption map is given by
f : m → m + k (mod N).
The shift algorithm is a special case of an affine cipher. Recall that an affine map on a ring R is a function f (x) = ax + b with a, b, x ∈ R. We apply such a map to the ring of integers modulo n, that is, R = n, as the encryption map. Specifically suppose we have an N letter alphabet and consider the letters as the integers 0,1,…, N-1 (mod N), that is in the ring N. We choose integers a, b ∈N with the greatest common divisor (a, )N = 1 and b ≠ 0. a, b are called the keys of the cryptosystem. The encryption map is then given by
f : m → am + b (mod N).
Example 1.4.1. Using an affine cipher with the English language and keys a = 3, b = 5 encode the message EAT AT JOE’S. Ignore spaces and punctuation.
The numerical sequence for the message ignoring the spaces and punctuation is
4,0,19,0,19,9,14,4,18.
Applying the map f (m) = 3m + 5 (mod 26), we get
17, 5, 62, 5, 62,32,47,17, 59 → 17, 5,10, 5,10, 6, 21,17, 7.
Now rewriting these as letters we get
Doing this to the other message units we obtainEAT AT JOE’S → RFKFKGVRH.
Since (a, N) = 1 the integer a has a multiplicative inverse modulo N. The decryption map for an affine cipher with keys a, b is then
g = f-1 : m → a-1(m - b) (mod N).
Since an affine cipher, as given above, goes letter to letter it is easy to attack using a statistical frequency approach. Further if an attacker can determine two letters and knows that it is an affine cipher the keys can be determined and the code broken. For example suppose the affine cipher is
f (n) ≡ an + b (mod N)
and an attacker has learned that f(n1) = m1,f(n2) = m2. This gives the attacker a two-by-two system of linear equations
an1 + b = m1
an2 + b = m2.
This is easily solvable for a, b, if (n1 - n2, N) = 1, breaking the code.
To provide better security in an affine cipher it is preferable to use k-vectors of letters as message units. In this case the form of an affine cipher becomes
f : v → Av + B
where v and B are k-vectors from 
and A is an invertible k×k matrix with entries from the ring N. Here the computations are done modulo N. Since v is a k-vector and A is a k × k matrix the matrix product Av produces another k-vector from . Adding the k-vector B again produces a k-vector so the ciphertext message unit is also a k-vector. The keys for this affine cryptosystem are the enciphering matrix A and the shift vector B. The matrix A is chosen to be invertible over N. This condition is equivalent to the determinant of A being a unit in the ring N. The decryption map is given by
v → A-1(v - B).
Here A-1 is the matrix inverse over N of A and v is a k-vector. The enciphering matrix A and the shift vector B are now the keys of the cryptosystem.
A statistical frequency attack on such a cryptosystem requires knowledge, within a given language, of the statistical frequency of k-strings of letters. This is more difficult to determine than the statistical frequency of single letters. As for a letter to letter affine cipher, if k + 1 message units, where k is the message block length, are discovered, then the code can be broken. As in the example for a cipher on single letters in this an attacker obtains a (k + 1) × (k + 1) system of linear equations which can be solved (see exercises).
Example 1.4.2. Using an affine cipher with message units of length 2 in the English language and keys
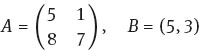
encode the message EAT AT JOE’S. Again ignore spaces and punctuation.
Message units of length 2, that is 2-vectors of letters are called digraphs. We first must place the plaintext message in terms of these message units. The numerical sequence for the message EAT AT JOE’s ignoring the spaces and punctuation is as before
4,0,19,0,19,9,14,4,18.
Therefore the message units are
(4,0) , (19, 0), (19,9), (14,4), (18,18)
repeating the last letter to end the message.
The enciphering matrix A has determinant 1 which is a unit modulo 26 and hence is invertible so it is a valid key.
Now we must apply the map f(v) ≡ Av + B (mod 26) to each digraph. For example
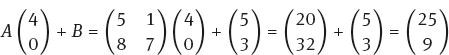
where everything is done modulo 26.
Doing this to the other message units we obtain
(25,9), (22, 25), (5,10), (1,13), (9,13).
Now rewriting these as digraphs of letters we get
(Z, J), (W, Z), (F, K), (B, N ), (J, N).
Therefore the coded message is
Example 1.4.3. Suppose we receive the message ZJWZFKBNJN and we wish to decode it. We know that an affine cipher with message units of length 2 in the English language and keys
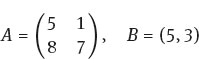
are being used.
The decryption map is given by
v → A-1(v - B)
so we must find the inverse matrix for A. For a 2 × 2 invertible matrix 
we have
Therefore in this case, recalling that multiplication is modulo 26,
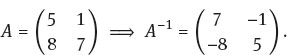
The message ZJWZFKBNJN in terms of message units is
(25, 9), (22, 25), (5,10), (1,13), (9,13).
We apply the decryption map to each digraph. For example
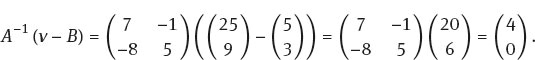
Doing this to each digraph we obtain
(4,0) , (19,0), (19,9), (14,4), (18,18)
and rewriting in terms of letters
(E, A), (T, A), (T, J), (O, E), (S, S).
This gives us
ZJWZFKBNJN → EATATJOESS.
1.5 Public Key Cryptography
Presently there are many instances where secure information must be sent over open communication lines. These include, for example, banking and financial transactions, purchasing items via credit cards over the internet and similar things. This led to the development of public key cryptography. Roughly, in classical cryptography only the sender and receiver know the encoding and decoding methods. Further it is a feature of such cryptosystems, such as the ones that we’ve looked at, that if the encrypting method is known then the decrypting can be carried out. In public key cryptography the encryption method is public knowledge but only the receiver knows how to decode. More precisely in a classical cryptosystem once the encrypting algorithm is known the decryption algorithm can be implemented in approximately the same order of magnitude of time. In a public key cryptosystem, developed first by Diffie and Hellman, the decryption algorithm is much more difficult to implement. This difficulty depends on the type of computing machinery used, and as computers get better, new and more secure public key cryptosystems become necessary.
The basic idea in a public key cryptosystem is to have a one-way function or trapdoor function. That is a function which is easy to implement but very hard to invert. Hence it becomes simple to encrypt a message but very hard, unless you know the inverse, to decrypt. The trapdoor is the simple knowledge that one needs to invert.
The standard model for public key systems is the following. We suppose that Alice’s public key is an injective map fA from the set of plaintext message units to the set of ciphertext message units. This map fA is made public. Alice’s private key is gA, the left inverse of fA and is held by her in secret. Since gA is the left inverse of fA it follows that for any message m we have gA(fA(m)) = m. Similarly Bob has a public key fB that is public knowledge and a private key gB that he holds secretly.
Alice wants to send a message to Bob. The encrypting map fA for Alice is public knowledge as well as the encrypting map fB for Bob. On the other hand, the decryption algorithms gA and gB are secret and known only to Alice and Bob respectively. Let m be the message Alice wants to send to Bob. She sends fB(m). The map fB is public knowledge and it is easy to encrypt. To decrypt Bob now applies gB to what he has received. Recall that presumably only he knows his private key gB. Doing this he obtains
and hence recovers the message.
If Bob receives a message how can he be certain that it actually comes from Alice. Within this standard model it is relatively easy to build in verification or authentication. As above let m be the message Alice wants to send to Bob. Now instead of sending fB(m) she sends
Now to decode Bob applies first gB, which is his private key that only he knows. This gives him
He then looks up fA which is publicly available and applies
to obtain the message. This supplies verification and authentication in the following manner. Suppose m is Alice’s verification; signature, social security number etc. If Bob receives fB(m) it could be sent by anyone since fB is public. On the other hand, since only Alice supposedly knows gA getting a reasonable message from fA(gBfBgA(m)) would verify that it is from Alice. Applying gB alone should result in nonsense.
Getting a reasonable one-way function can be a formidable task. Presently, the most widely used public key systems are based on difficult to invert number theoretic functions. Diffie-Hellman in 1976 developed the original public key idea using the discrete logarithm problem usually abbreviated to discrete log problem or DLP.
In modular arithmetic it is easy to raise an element to a power but difficult to determine, given an element, if it is a power of another element. Specifically if G is a finite group, such as the cyclic multiplicative group of p where p is a prime, and h = gk for some k then the discrete logarithm or discrete log of h to the base g is any integer t with h = gt. In the Diffie-Hellman system there is a public key exchange between the communicating parties based on the discrete log problem. This public key will indicate a private encryption system.
In 1977 Rivest, Adelman and Shamir developed the RSA algorithm which is presently one of the most widely used public key cryptosystems. It is based on the difficulty of factoring large integers and in particular on the fact that it is easier to test for primality than to factor. As in the Diffie-Hellman protocol there is a public key exchange using the difficulty of factoring followed by an encryption.
We will discuss both the Diffie-Hellman protocol and the RSA protocolin detail in Chapter 7.
1.6 Cryptosystems and the Key Space
In the beginning of this chapter we defined a basic cryptosystem as a tuple where P is the set of plaintext message units, C is the set of ciphertext message units, f is an injective map from P to C, and g is its left inverse. The map f is the encryption map or encryption algorithm, while its left inverse g is the decryption map or decryption algorithm. Now we place this in a more general context. We call this wider model a (general) cryptosystem. Roughly, a (general) cryptosystem is an indexed collection of basic cryptosystems, indexed by a set K called the key space. Formally, it is defined as follows.
Definition 1.6.1. A cryptosystem is a tuple 
where
The elements k ∈ K are called keys.
indexed by the key space. This is called the set of encryption maps. Hence, for each k ∈ K, there is an injective map fk : P → C.
also indexed by the key space. This is called the set of decryption maps.
The central property of a cryptosystem is that, for each k ∈ K, there exists a corresponding key k’ ∈ K and a decryption map 
such that gk’ is the left inverse of fk. In other words, for every plaintext message unit m, we have gk’ (fk(m)) = m.
In our previous language this means that for each k ∈ K we have a basic cryptosystem 
. To place further emphasis on the key space, we say that for every encryption map 
, the index k is the corresponding encryption key, and for every decryption map 
, the corresponding index k’ is called the decryption key.
Using this model, we can easily distinguish symmetric from asymmetric cryptosystems. In a symmetric key cryptosystem, if the encryption key k is given, it is easy to find the corresponding decryption key k’. In fact, most of the time we have k’ = k. In an asymmetric or public key cryptosystem, even if the encryption key k is known, it is infeasible to find or compute the decryption key k’. This is of course equivalent to how it was phrased in the short description in Section 1.5: if the encryption map is known, it is infeasible to find the inverse. In most public key cryptosystems the encryption key is made public while the decryption key is secret and known only to the party receiving the communication.
Notice that the key space must be fairly extensive to prevent a potential attacker from simply doing an exhaustive search to find the decryption key. Before we discuss specific cryptosystems, we introduce general cryptographic protocols.
1.7 Cryptographic Protocols
Besides secure confidential message transmission there are many other tasks that are important in cryptography, both public key and symmetric key. Although it is not entirely precise, we say that a cryptographic task is where one or more people must communicate with some degree of secrecy. The set of algorithms and procedures needed to accomplish a cryptographic task is called a cryptographic protocol. A cryptosystem is just one type of cryptographic protocol.
Definition 1.7.1. Suppose that several parties want to manage a cryptographical task. Then they must communicate with each and cooperate. Hence each party must follow certain rules and implement certain agreed upon algorithms. The set of all such methods and rules to perform a cryptographical task is called a cryptographic protocol. We now list several cryptographic tasks. These will be discussed in more detail later in the book together with cryptographic protocols to implement them.
(1) Authentication: This is the process of determining that a message, supposedly from a given person, both does come from that person and has not been tampered with. Included in authentication are the concepts of hash functions and digital signatures. Hash functions will be discussed in Chapter 2. Another important usage is password identification. We will discuss a secure backup password system using non-commutative methods later in the book.
(2) Key Exchange and Key Transport: In a key exchange two people usually called Bob and Alice exchange a secret shared key to be used in some symmetric encryption. In a key transport one party transports to another a secret key that is to be used.
(3) Secret Sharing: This is a method where some secret is to be shared by k people but not available to any proper subset of them. There is a beautiful simple solution to the general problem given by Shamir. We will describe this also in Chapter 2.
(4) Zero Knowledge Proof This is an argument that convinces someone that you have solved a problem, for example a combinatorial problem, without giving away the solution. This is tied to authentication.
We will look in detail at protocols for each of these cryptographic tasks in Chapter 4.
1.8 Exercises
1.1 Is every encryption map with a finite set of ciphertexts surjective?
1.2 If we encrypt using a shift cipher explain why discovering one encrypted letter will break the system?
1.3 All integers can be expressed in binary form, that is only using digits of 0,1. Explain why in a number theoretic cipher it is only really necessary to encrypt a bit, that is, encrypt a 0 or a 1?
1.4 Suppose we have an encryption system and we have a method that correctly guesses each encrypted letter with a probability of 0.5. If we have a message 20 letters long, what is the probability of randomly guessing the plaintext? (Randomly guessing indicates that guessing two letters in a row are independent and hence the probabilities multiply.)
1.5 Encrypt the message NO MORE WAR using an affine cipher with single letter keys a = 7, b = 5.
1.6 An encryption is done letter by letter using an affine cipher with single letter keys a, b. Using the English alphabet so that N = 26 we find that 6 is encrypted by 23 and 15 is encrypted by 24. What are the keys a, b?
1.7 Encrypt the message NO MORE WAR using an affine cipher on two vectors of letters and an encrypting key
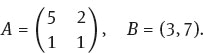
1.8 What is the decryption algorithm for the affine cipher given in the last problem?
1.9 How many different affine enciphering transformations are there on single letters with an N letter alphabet?
1.10 If we use an affine cipher on N, N ≥ 2, single letters with n → an + b with b not congruent to 0 modulo N and (a -1, N) = 1, show that there is always a unique fixed letter. (This can be used in cryptanalysis).
1.11 Let N ∈ 
with N ≥ 2 and n → an + b with (a, N) = 1 be an affine cipher on an N letter alphabet. Show that if any two letters are guessed n1 → m1, n2 → m2 with (n1 - n2, N) = 1 then the code can be broken.
1.12 Let A be an N-letter alphabet. As before consider A as N and treat them as the modular ring. Consider plaintext messages as elements of N and consider the encryption map f (n) = n2 (mod N). Is this a good encryption map? Why or why not?