13 Commutative Gröbner Basis Methods
13.1 Commutative Gröbner Bases
Besides numbers and group elements, polynomials are natural objects to use in algebraic cryptography. Recall that a polynomial f is a formal linear combination f = c1t1 + ··· + csts whose coefficients ci are taken in a field K and where the elements ti are terms, that is power products ![]() of indeterminates xi. The set of all polynomials of this form is called the polynomial ring P = K[x1,..., xn]. This set is a commutative ring with identity. In other words, polynomials can be added and multiplied in a natural way and the usual rules such as the associative and distributive laws hold.
of indeterminates xi. The set of all polynomials of this form is called the polynomial ring P = K[x1,..., xn]. This set is a commutative ring with identity. In other words, polynomials can be added and multiplied in a natural way and the usual rules such as the associative and distributive laws hold.
Example 13.1.1. Using the base field K = ℚ and the indeterminates x, y, z, we can add the polynomials f = xy + yz and g = x2 + xy and obtain f + g = x2 + 2xy + yz. Their product equals f · g = x3y + x2y2 + x2yz + xy2z. Notice that we can also factor f and g in the form f = y(x + z) and g = x(x + y).
For cryptographic applications, we need to work effectively with polynomials. The main tool for effective calculations with polynomials and polynomial ideals are Grobner bases. The first task we have to solve is to make equality of polynomials effective and to store them efficiently. How is it possible to detect in the preceding example that the polynomial xy2z + x2y2 + x3y + x2yz equals f · g? Clearly, we need to order the terms in a unique way.
Definition 13.1.2. Let x1,...,xn be indeterminates, and let
![]()
be the set of terms in these indeterminates. A complete ordering relation a is called a term ordering on ![]() if the following conditions are satisfied.
if the following conditions are satisfied.
(1) The relation a is multiplicative, that is, if two terms t1, t2 ϵ ![]() satisfy t1 ≤σ t2 and if t3 ϵ
satisfy t1 ≤σ t2 and if t3 ϵ ![]() then we have t1t3 ≤σ t2t3.
then we have t1t3 ≤σ t2t3.
(2) The relation a is a well-ordering, that is, every decending chain t1 ≥σ t2 ≥σ ··· in ![]() is eventually stationary.
is eventually stationary.
It is easy to see that the second condition is equivalent to requiring t ≥σ 1 for all t ϵ ![]() . There exist plenty of term orderings, and many of them have special useful properties. The following example introduces two well-known term orderings.
. There exist plenty of term orderings, and many of them have special useful properties. The following example introduces two well-known term orderings.
Example 13.1.3. Let ![]() be the set of terms in the indeterminates x1,..., xn.
be the set of terms in the indeterminates x1,..., xn.
(1) For ![]() and
and ![]() we let t ≤lex t′ if and only if one of the following conditions holds:
we let t ≤lex t′ if and only if one of the following conditions holds:
– α1 = β1 and α2 < β2
– ⋮
– α1 = β1,..., αn-1 = βn-1 and αn < βn
– t = t′
It is easy to check that this defines a term ordering ≤lex on ![]() . It is called the lexicographic term ordering.
. It is called the lexicographic term ordering.
(2) For practical computations, the most well-known and useful term ordering is the degree reverse lexicographic term ordering ≤drl . It is defined by letting t ≤drl t′ for ![]() and if and only if t = t′ or one of the following conditions is satisfied:
and if and only if t = t′ or one of the following conditions is satisfied:
– deg(t) = α1 + · + αn < deg(t′) = β1 + · + βn
– deg(t) = deg(t′) and αn > βn
– deg(t) = deg(t′), αn = βn and αn-1 > βn-1
– deg(t) = deg(t′), αn = βn,..., α;3 = α3 and α2 > β2
It is straightforward to verify that these conditions indeed define a term ordering.
Given a term ordering σ, there is a natural way to represent a non-zero polynomial f ∊ P, namely to write f = c1t1 + · + csts with cj ∊ K and terms tj ∊ ![]() satisfying t1 >σ · >σ ts. Using these representations, we can now define several notions which are central to Grobner basis theory.
satisfying t1 >σ · >σ ts. Using these representations, we can now define several notions which are central to Grobner basis theory.
Definition 13.1.4. Let σ be a term ordering on Tn, and letf = c1t1 + · + csts € P {0} be represented as above.
(1) The term Lt(f) = t1 is called the leading term off with respect to σ.
(2) The field element Lc(f) = c1 is called the leading coefficient of f with respect to σ.
(3) The polynomial Lm(f) = c1t1 is called the leading monomial of f with respect to σ.
For instance, the polynomial f = x2 + xy + y3 satisfies Ltlex(f) = x2 and Ltdrl(f) = y3. These definitions can be extended to polynomial ideals. A set of polynomials I is called an ideal in P if it is a subgroup with respect to addition and if it has the property that f ϵ I and g ϵ P imply fg ϵ I. Important examples of ideals are obtained as follows.
Example 13.1.5. Let I be a subset of the polynomial ring P.
(1) If there exists a polynomial f ϵ P such that I = [fg | g ϵ P} then I is called the principal ideal generated by f and is denoted by I = (f).
(2) More generally, if there exist polynomials f1,...,fs ϵ P such that I = [f1g1 + · + fsgs | gi ϵ P} then I is called the ideal generated by f1,...,fs and is denoted by I = (f1,...,fs).
As an application of Grobner basis theory we shall see that, in fact, every ideal in P is of the type described in the preceding example. But first we generalize the notion of a leading term as follows.
Definition 13.1.6. Let σ bea term ordering on Tn, and let I be an ideal in P. Then the ideal
Ltσ (I) = (Ltσ (f) | f ϵ I)
= [f1g1 + · + fsgs | s ≥ 0, f1 ϵ I, gj ϵ P}
is called the leading term ideal of I with respect to σ.
At this point we encounter a problem which is one of the main incentives to introduce Gröbner bases, namely the fact that the leading terms of a set of generating polynomials need not generate the leading term ideal of an ideal. The following example is a case in point.
Example 13.1.7. Let P = K[x, y],let σ = drl, and letI = (f1, f2) be the polynomial ideal generated by f1 = x2 - 1 and f2 = xy - 1. Then we have x - y = yf1 - xf2 ϵ I and therefore x = Ltσ(x - y) ϵ Ltσ (I). Thus the inclusion (Ltσ(f1), Ltσ(f2)) c Ltσ(I) is strict.
This example leads us to the following definition.
Definition 13.1.8. Let σ be a term ordering on Tn,let I c P be a polynomial ideal, and let G c I be a subset of I. The set G is called a σ -Gröbner basis of I if Ltσ (I) = (Ltσ (g) | g ϵ G), that is if the leading term ideal of I is generated by the leading terms of the polynomials in G.
For instance, the polynomials in the preceding example can be extended to a Gröbner basis of I as follows.
Example 13.1.9. In the setting of the preceding example, let f3 = x - y ϵ I and f4 = ff - yf3 = y2 - 1 ϵ I. Then the set G = {/1, ff, f3, f4} satisfies (Ltff (/1),..., Ltff f)) = (x2,xy, x,y2) = (x,y2).Usingf3 andf4, it is not difficult to show that no polynomial of the form c1y + c2 with non-zero constants c1 or c2 is contained in I. Hence we have Ltσ (I) = (x, y2) and it follows that G is a σ - Gröbner basis of I.
In general, every finite set of polynomials generating an ideal I can be extended to a finite Gröbner basis of I. This is achieved by Buchberger’s Algorithm. To introduce this algorithm, we first have to describe the multivariate version of polynomial division.
Proposition 13.1.10 (The Division Algorithm). Let P = K[x1,...,xn ], let a be a term ordering on Tn, and letf, g1,..., gs ϵ P. Consider the following instructions.
(1) Let q1 = · = qs = r = 0 and h = f.
(2) Repeat the following steps until h = 0. Then return (q1,..., qs) and r and stop.
(3) Repeat the following step as often as possible.
(4) Find the smallest i ϵ {1,..., s} such that Ltσ (h) is a multiple of Ltσ (gj). Ifsuch an i exists, replace qj by qj + Lmσ (h)/ Lmσ (gj) and hbyh - (Lmσ (h)/ Lmσ (gj)) gj.
(5) Replace r by r + Lmσ (h) and hbyh - Lmσ (h).
This is an algorithm which computes (q1,..., qs) ϵ Ps and r ϵ P such that f = q1g1 + · + qg + r and such that the following conditions hold.
(1) No term ofr is divisible by any of the terms in [Ltσ (g1),..., Ltσ (gs)}.
(2) For all i such that qj = 0 we have Ltσ (qjgj) <σ Ltσ (f).
Proof. Since the leading term of h becomes smaller with respect to σ during each execution of (4) or (5), and since σ isa term ordering, the algorithm is finite. Next we note that the equality f = q1g1 + · + qsgs + h + r holds throughout the execution of the algorithm. Since the algorithm stops when it reaches h = 0, we obtain the desired equality. The fact that the two additional conditions hold follows immediately from the descriptions of steps (4) and (5).
The division algorithm produces a polynomial NRa G(f) = r which depends on the order of the elements in G = (g1,... ,gs). This polynomial is called the normal remainder of f with respect to G. Besides the Division Algorithm, we need one further ingredient for Buchberger’s Algorithm.
Definition 13.1.11. Let σ be a term ordering, let fj, fj ϵ P {0}, and let Lmσ(fk) = cktk with ck ϵ K and tk ϵ Tn for k ϵ {, j}. Then we let tjj = lcm(tj, tj)/tj and j = lcm(tj, t;-)/t;- and call the polynomial Sjj = 1 tjjfj - 1 j fj the S-polynomial of fj and fj.
The idea behind the definition of Sjj is that both tj fj and j fj have thesameleading term lcm(tj, tj) and that this term cancels in Sjj. Therefore the polynomial Sjj has a chance to produce a “new” leading term, and this is used in Buchberger’s Algorithm as follows.
Theorem 13.1.12 (Buchberger’s Algorithm). Let P = K[x1,.. .,xn], let a be a term ordering on Tn, and letf1,..., fs ϵ P be non-zero polynomials which generate an ideal I = (f1,...,fs). Consider the following instructions.
(1) Let G = (f1,... ,fs) and B = {(i, j) | 1 < i < j < s}.
(2) Repeat the following steps until B = 0. Then return G and stop.
(3) Choose a pair (i, j) ϵ B and remove it from B.
(4) Compute the S-polynomial Sjj off and fj and its normal remainder Sj = NRa >G(Sy). IfSj = 0 then continue with step (2).
(5) Increase s by one, append fs = Sjto G, and append {(i, s) | 1 < i < s - 1} toB. Then continue with step (2).
This is an algorithm which computes a a-Grobner basis G of the ideal I.
For a proof of the finiteness and correctness of this algorithm, we refer to [KR1], Section 2.5. To get a feeling for the performance of this algorithm, let us apply it in the case of Example 13.1.7.
Example 13.1.13. Let P = K[x,y], let σ = drl, and let f1 = x2 - 1 and f2 = xy - 1. Following Buchberger’s Algorithm, we compute S12 = yf1 - xf2 = x - y and S12 = S12 and appendf3 = S12 = x - y to G. At this point we have B = {(1,3), (2,3)}.
Working on the pair (1,3) yields S13 = f1 - xf3 = xy - 1 andS’13 = 0. Next we check the pair (2,3) and get S23 = f2 - yf3 = y2 - 1 and S’23 = S23. Thus we appendf4 = y2 - 1 to G and have B = {(1,4), (2,4), (3,4)}. Working out these three pairs produces Sj = 0 each time, so that the algorithm returns G = (f1,f2,f3,f4) and stops.
Gröbner bases and Buchberger’s Algorithm have numerous applications in computational algebra. We end this section by listing a few of them which will be of use for algebraic cryptography. For detailed proofs of these results, we refer to [KR1].
Proposition 13.1.14 (Macaulay’s Basis Theorem). Let f1,...,fs e P be polynomials which generate an ideal I = (f1,... ,fs). We choose a term ordering a and use Buchberger’s Algorithm to compute a a-Gröbner basis G = (g1,..., gt) of I. Then the residue classes ofthe terms in the set
Oσ (I) = Tn Ltσ (I) = {t e Tn | no term Ltσ (g¡) divides t}
form a K-vector space basis of P/I.
Proposition 13.1.15 (Ideal Membership Test). Given apolynomial ideal I and apolyno- mialf e P, we can check as follows whether f e I holds:
(1) Choose a term ordering a and use Buchberger’s Algorithm to compute a a - Gröbner basis G of I.
(2) Using the Division Algorithm, check whether NRa G(f) = 0.
13.2 Commutative Gröbner Basis Cryptosystems
The computation of a Gröbner basis using Buchberger’s Algorithm has a very high worst-case complexity: EXPSPACE. The idea underlying Gröbner basis cryptosystems is to utilize this fact by constructing a cryptosystem whose security depends on the difficulty of computing a certain Gröbner basis. The first such cryptosystem was suggested by M. Fellows and N. Koblitz in 1994 (see [FK]) and is called the Polly Cracker Cryptosystem.
Polly Cracker Key Generation
Let K be a finite field and P = K[x1, ...,xn] a polynomial ring over K. Suppose that Bob wants to send a message m to Alice. The message space we use is P = K, and the ciphertext space is c = P. The secret Key k will be an element of K = Kn. To generate it, we choose a random vector k = (a1,..., an)in Kn.
Next Alice chooses s > 1 and random polynomials f1,..., fs ϵ P. Then she computes the polynomialsgj = fj - fj(a1,..., an)for i = 1,...,s. The tuple (g1,... ,gs) ϵ P will serve as Alice’s public Key.
Encryption and Decryption
To encrypt a message m ϵ K, Bob chooses random polynomials h1,...,hs ϵ P and computes the ciphertext polynomial c = m + h1g1 + · + hsgs. In order to decrypt a ciphertext unit c ϵ P, Alice evaluates c(a1,..., an) and obtains the original message unit m.
The correctness of this cryptosystem follows from the fact that we have
![]()
and thus
![]()
How is this cryptosystem related to Gröbner bases? Let us analyse its security. To decrypt a ciphertext unit c ϵ P, an attacker has to find an element z ϵ K such that c + z is contained in the ideal I = (g1,...,gs). To do this, he may try to compute a Gröbner basis G of I and then determine z using the equality z = NRa G(c). Hence the Polly Cracker cryptosystem is not secure if an attacker is able to compute a Gröbner basis of I.
To make matters worse, the attacker may actually get away with computing a small part of a Gröbner basis of I. In the computation of the normal remainder NRa G(c), only finitely many elements of the Gröbner basis G are used. Hence it may suffice to determine a partial Gröbner basis in order to decipher a single message.
A further weakness of the Polly Cracker cryptosystem is revealed by a statistical analysis of the ciphertext. In the computation of c = m + h1g1 + · + hsgs, usually only a small percentage of the terms cancels out completely. Most terms of the products hjgj will be contained in the ciphertext. Thus, if t is a term occurring in one of the secret polynomials gj, many of its multiples will tend to show up in the ciphertext polynomial c. It is clear that a careful statistical analysis of greatest common divisors of the terms in c may reveal individual terms t. Then one can simplify the corresponding polynomial ht and create a simpler ciphertext for the same message. By repeating this construction, it is frequently possible to decipher c.
In spite of these problems, Koblitz suggested in [Ko2], Ch. 5, several special cases of Polly Cracker cryptosystems whose security seems to be high at first glance.
Example 13.2.1 (The Graph-3-Colouring Cryptosystem). A graph is a pair r = (V, E) consisting of a set of vertices V = {v1,..., vr} and a set of edges E = {e1,..., es} c V x V, each of which connects two vertices. A 3-colouring of a graph r = (V, E) is

Fig. 13.1: 3-colourable.
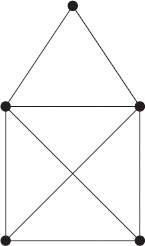
Fig. 13.2: not 3-colourable.
a map $ : V —> Z3 such that $ (v,) = $ (v;) whenever there is an edge ek = (vj, Vj) connecting vj and Vj. The graph r is called 3-colourable if a 3-colouring exists.
Given a graph r, the following two problems are NP-hard:
– Decision problem: Is r 3-colourable?
– Search problem: If r is 3-colourable, find a 3-colouring!
Based on these problems, we construct a Polly Cracker cryptosystem as follows. Alice chooses a suitable 3-colourable graph r = (V, E) for which she Knows a 3-colouring. (The question which graphs could be considered suitable will be discussed below.) Thus her secret Key is a tuple (ajj) ϵ V xZ3 such that
![]()
Alice’s public Key then consists of the following 4r + 3s polynomials in the ring K[xjj |
i ϵ {1,.. .,r}, j ϵ {0,1,2}], where K = Z3 = {0,1,2}, r = #V, ands = #E:
– fj = xj1 + xj2 + xj3 - 1for i = 1,..., r
– gjjk = xjjxjk for i = 1,..., r and 0 < j < k < 2
– hjjk = xjkj if (i, j) ϵ E and 0 < j < 2
Based these Keys, Alice and Bob use the Polly Cracker cryptosystem.
The following observations show that the security of this cryptosystem relies on the difficulty of solving the 3-colouring search problem. First we check that (ajj) is a common zero of the polynomials in the public Key.
(1) For i = 1,..., r,we havef (aj0, a^, aj2) = aj0 + aj1 + aj2 - 1 = 0, since every vertex has precisely one colour.
(2) For i = 1,..., r and 0 < j < k < 2, we havegjjk(aj0, aj1, aj2) = ajjajk = 0 since every vertex has precisely one colour.
(3) For i,j ϵ {1,...,r} such that (i,j) ϵ E and for every k ϵ {0,1,2}, we have hjjk(aj0, aj1, aj2) = ajkajk = 0 because not both vertices vj and vj have colour K.
Conversely, let us show that every common zero (c j of the polynomials in the public Key yields a 3-colouring of r.
(4) Since cjjcjk = 0 for j = K, at most one of the numbers {cj0, cj1, cj2} is non-zero.
(5) Since cj0 + cj1 + cj2 = 1, it follows that precisely one of the numbers {cj0, cj1, cj2} is one and the other two are zero.
(6) Since cjkcjk = 0 for (i, j) ϵ E, two vertices which are connected by an edge have different colours.
The upshot of this discussion is that the Knowledge of a 3-colouring of r is sufficient to break the graph 3-colouring cryptosystem. Finding a 3-colouring is equivalent to computing a common zero (ajj) of the set of public polynomials, and therefore equivalent to computing a Gröbner basis G = {xjj - atj | i ϵ {1,..., r}, j ϵ {0,1,2}} of an ideal containing the public polynomials. If we find a graph for which a 3-colouring is hard to find, a Gröbner basis of this Kind will be hard to compute.
So, what is the problem with this construction? First of all, we have to find a suitable graph. For most concrete instances of the graph 3-colouring search problem, the actual complexity will be much lower than the worst-case complexity. In fact, in most cases it will be linear in the size of r. Therefore we may have to choose very large graphs to make this problem infeasible. However, then we create a very large public Key {fj, gjjk, hjjk} and the amount of data that we have to transmit in order to send a message consisting of a single element of Z3 is huge. In other words, the data rate of this cryptosystem will be abysmal. Finally, we still face the problem to choose the graph r (and thus the public Key polynomials) such that the attacks using partial Gröbner bases and statistical analysis of the terms in the ciphertext become infeasible.
Until now, nobody has been able to find a convincing simultaneous solution to the problems inherent in the Polly Cracker cryptosystem. In order to get a wider choice of constructions, we introduce a far-reaching generalization, namely the general Commutative Gröbner Basis Cryptosystem (CGBC).
CGBC Setup and Key Generation
Let K be a finite field, let P = K[x1,.. .,xn], let σ be a term ordering on Tn, let I c P be an ideal, and let G = {g1,...,gs} be a σ -Gröbner basis of I. The set G will serve as Alice’s secret Key. To construct a public Key, she chooses a set of terms O in Tn Ltσ (I). The K-vector space P = (O)K generated by O is the set of plaintext units for the CGBC. The set of ciphertext units will be c = P. Finally, Alice chooses suitable polynomials f1,... ,ft ϵ I which constitute the public Key of the CGBC. (The correct interpretation of “suitable” will be discussed below.)
CGBC Encryption and Decryption
Let m ϵ (O}K be the plaintext unit that Bob wants to send to Alice. He chooses suitable (e.g., sufficiently random) polynomials h1,...,ht ϵ P and computes c = m + h1f1 + · + htft. To decrypt a ciphertext unit c ϵ P, Alice calculates m = NRa G(c).
The correctness of this procedure follows from fact that division by a Gröbner basis yields an ideal membership test (see Prop. 13.1.15). For m’ = NRa G(c) we have m’ = c (mod I), and therefore m’ - m = 0 (modI). Since m and m’ are constants and I = P, they have to be equal.
General commutative Gröbner basis cryptosystems face a number of possible attacks by Eve, the evil attacker. Let us discuss some of them.
(1) Obviously, the cryptosystem can be broken if Eve succeeds in computing any Gröbner basis of I. One difficulty may be that she does not Know I, but only a smaller ideal J = (f1,...,ft} for which a Gröbner basis may be hard to come by. On the other hand, it suffices for Eve to find any Gröbner basis of any ideal containing J.
(2) As for the Polly Cracker cryptosystem, Eve can decipher an individual ciphertext unit c if she Knows a sufficiently large partial Gröbner basis of J (or I). The reason is that, in the division steps reducing c —> NRa G(c), only some of the elements of G are involved.
(3) In the calculation of a ciphertext unit c = m + h1f1 + · + htft, usually not many terms in the polynomials hifi cancel out completely. Unless special care is taken in the choice of the coefficient polynomials hj, large subsets of the terms in c will have non-trivial greatest common divisors. Using statistical analysis, Eve may determine individual terms in hj and simplify the ciphertext without changing the underlying plaintext.
(4) In the computation of c, a large amount of cancellation of higher-degree terms has to occur to make the following Linear Algebra Attack infeasible: Eve guesses a degree bound for the polynomials hi and writes them down using indeterminate coefficients. Then the equality c = m + h1f1 + · + htft yields a linear system of equations for these unknown coefficients. In addition, Eve may proceed to solve this system degree by degree (with respect to the terms in c) and utilize heuristics to exclude the appearance of certain terms in the polynomials hj, thereby reducing the sizes of the partial linear systems of equations.
(5) Finally, Eve may resort to a chosen-ciphertext-attack. If she is able to decipher illegal ciphertexts consisting of the terms tj generating Ltσ (I), she may construct a Gröbner basis {g1, ...,gs} of I via gj = tj - NRa >G(tj). Hence Alice has to restrict the set of terms O defining the plaintext unit space such that illegal ciphertexts like tj are revealed by having terms from (Tn Ltσ (I)) O in their decryption. Then her decryption algorithm can reject illegal ciphertexts.
Altogether, it has proven quite difficult to generate secure instances of commutative Gröbner basis cryptosystems, in particular if the need for an acceptable data rate is taken into account. Nevertheless, finding a large enough number of such instances is an attractive goal. We have seen that it is possible to encode NP-hard problems into the task of computing a Gröbner basis. Thus Gröbner basis cryptosystems are candidates for Post Quantum Cryptography. Later we study suggestions to overcome the aforementioned difficulties by resorting to non-commutative algebraic structures (such as free associative algebras or certain group rings) which support analogous Gröbner basis theories.
13.3 Algebraic Attacks Using Gröbner Bases
After seeing the difficulties involved in using (commutative) Gröbner bases for constructing new cryptosystems, let us turn the tables and try to use Gröbner bases to break existing cryptosystems. This topic is Known as algebraic attacks and has gained widespread attention after F. C. Faugere used it to meet the HFE Challenge (see [Fau]). Let us explain the basic idea first.
Every encryption map of a cryptosystem can be represented by a map sending bit- tuples to bit-tuples. Mathematically, we represent it as a map e : Zf —> Zf where P cZf and c cZf .A map like this is always polynomial, that is for K = Z2 there exist polynomialsf1,...,fs ϵ K[x1, ...,xn] such that
![]()
for all (a1,..., an) ϵ Kn. Of course, these polynomials f1,... ,fs are not uniquely determined. Suppose that g1,...,gs ϵ K[x1, ...,xn] are further polynomials with the property that
for all (a1, . . . , an) P. Then the differences fi .gi are contained i he vanishing ideal
![]()
of P. It is easy to check that I(P) is in fact a polynomial ideal. Below we shall see an effective and efficient algorithm to compute a system of generators of this vanishing ideal. In this setting, we can mount different algebraic attacks using one of the following methods.
![]()
Remark 13.3.1 (Algebraic Known-Plaintext-Attack). Suppose that Alice and Bob are using a symmetric cipher and one or more plaintext-ciphertext pairs are Known to Eve. She represents the input bits of the encryption map by indeterminates x1,..., xn, certain bits of intermediate results by indeterminates yjj, and the bits of the unknown Key by indeterminates k1,...,ke. Then Eve writes down the encryption map e : Zf —> Zf using polynomialsf1,..., fs ϵ Z2 [x1,..., xn, {yjj}, K1,..., ke]. By substituting the Known plaintext-ciphertext pairs, Eve obtains a system of polynomial equations in the indeterminates yjj and K1,..., ke.
In many cases, this polynomial system of equations has a unique solution ({a,-,-}, b1,...,be) defined over Z2. In the language of Gröbner bases, this means that the ideal generated by those equations has the Gröbner basis G = {y, - a, }u{k1 - b1, ...,ke - be}. If Eve is able to compute that Gröbner basis, she can use the secret Key (b1,..., be) to decrypt further ciphertext units. She has broken the cryptosystem.
The situation of this remark can for instance occur if Bob encrypts a pdf-file (whose first four bytes are %PDF) and uses no further precautions. In less favourable situations Eve may still try to launch the following attack.
Remark 13.3.2 (Algebraic Ciphertext-Only-Attack). Suppose that Alice and Bob are using a symmetric cipher. Eve intercepts a number of ciphertext units. As in the preceding remark, she represents the encryption map e : ^2 —> Zj with polynomials
![]()
using different sets of indeterminates x1m),..., , y(,m) for every intercepted ciphertext unit, but the same indeterminates k1,...,ke for the Key bits. Then Eve tries to solve the resulting polynomial system for k1,...,kl and thereby break the cryptosystem.
It is clear that similar algebraic attacks can be mounted against public Key ciphers and stream ciphers. For the sake of brevity, we describe only the first case in more detail.
Remark 13.3.3 (Algebraic Attacks to Public Key Systems). Suppose that Alice and Bob use a public Key cryptosystem. Since Eve Knows the public Key, she can describe the encryption map e : Z2 —> using polynomials /1,...,/s e Z2[x1,...,xn] which do not involve any indeterminates related to the secret Key. Hence, if Eve want to attack a single ciphertext unit, it suffices to solve the polynomial system f(x1, ...,xn) = c, where i = 1,..., s and c, is the i-th bit of the ciphertext.
Eve may also decide to attack the public Key. For this purpose she describe the decryption map ô : Zj —> ^2 by polynomials gj(y1,..., ys, K1,..., ke) where the indeterminates y 1,..., ys represent the bits of the ciphertext and the indeterminates k1,...,ke represent the bits of the secret Key. Then Eve uses the publicly Known encryption map to create as many plaintext - ciphertext pairs as she needs and sets up arbitrarily many polynomial equations in the indeterminates k1,...,ke whose only solution over Z2 is the secret Key.
Let us apply this former method in an extremely simple case.
Example 13.3.4. Suppose that Alice and Bob are using the RSA cryptosystem with the public Keys n = 15, e =5 and the secret Key d = 5. (Notice that ÿ(15) = 8 and de = 1(mod 8).) The plaintext and ciphertext units are elements of (Z/15Z)X and will be represented by elements a0 + 2a1 + 4a2 + 8a3 with a, e {0,1}.
Then the encryption map e(a0, a1, a2, a3) = (c0, c1, c2, c3) is determined by c0 + 2 c1 + 4c2 + 8c3 = (a0 + 2a1 + 4a2 + 8a3)5. In view of the relations a2 = a, for a:j ϵ Z2, this yields the polynomial representation c0 = a0a1a2a3 + a0a1a2 + a0a2 + a0a3 + a2a3 + a0 + a3
c1 = a0a1a2a3 + a0a1a2 + a0a1 a3 + a0a2a3 + a0a1 + a1 + a2 + a3
c2 = a1a2a3 + a0a1 + a1a2 + a1a3 + a1 + a2
c3 = a0a1a2a3 + a0a1a2 + a1a2 a3 + a0a1 + a0a2 + a0a3 + a2a3 + a3.
For instance, if Eve intercepts the ciphertext bits (c0, c1, c2, c3) = (1,1,0,0), she can now compute a Gröbner basis of the ideal (fj(a0, a1, a2, a3) - c | i = 0,1, 2,3} where the polynomials fi correspond to the right-hand sides above. The result is G = {a0 - 1, a1 - 1, a2, a3}. This corresponds to the fact that the plaintext a0 + 2a1 + 4a2 + 8a3 = 3 encrypts to the given ciphertext.
At the heart of these algebraic attacks lies the problem of solving a large system of polynomial equations over a finite field K, where we usually have K = Z2. Letf1,..., fs ϵ K[x1,..., xn] be the polynomials which define the polynomial system
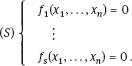
Each solution of the polynomial system (S) satisfies every equation of the form g1/1 + · + gs/s = Owhere gv..., gs ϵ K[x1,.. .,xn] are arbitrary polynomials. Inotherwords, each solution of (S) is a zero of the polynomial ideal I = (/1,...,/s). The set of all zeros of I is called the zero set of I and is denoted by Z(I).
Notice that we are always looking for solutions of the given polynomial systems which are defined over K, where K = Fq is a finite field. Therefore we my append the equations xf - x{ = 0 to the system in question to make sure that the computed solution is indeed an element of K (and not of a larger finite field). These equations are also called the base field equations and the ideal (x - x1,...,xf - xn) is called the base field ideal.
Before we address particular methods for solving large polynomial systems over finite fields, we want to point out algorithms which can be used to describe the encryption map via polynomials. One way is of course to trace the explicit description of the encryption map and to represent each step by polynomials. For certain steps (such as S-boxes) or certain encryption maps, we can try to consider them as black box algorithms and apply the following algorithm for multivariate polynomial interpolation.
Theorem 13.3.5 (The Buchberger-Möller Algorithm). Let K be a finite field and X = |(p1, K1),..., (ps, Ks)} afinite seto/pointsinKn xKe. Assume that the elementspi ϵ Kn are plaintext units and the elements K{ ϵ Kl are Keys o/a given cryptosystem. For i = 1,..., s, let (ci1,..., cim) ϵ Km be the ciphertext unit obtained by encryptingPj using the Key Kj.
Let Q be the polynomial ring Q = K[x1,..., xn, y1,..., ye] and leto be a term ordering on Q. Consider the/ollowing sequence o/instructions.
(1) Letg = 0, O = 0,S = 0,L = {1}, and M = (mj a matrix having initially s columns and 0 rows.
(2) I/L = 0 then continue with step (6). Otherwise, let t = mino (L).
(3) Compute eval(t) = (t(p1, K1),..., t(ps, Ks)) and row reduce this vector against the rows o/M. The result is o/the/orm
(v1,..., Vs) = eval(t) - £ ai • (miv..., mfe) i
with at ϵ K.
(4) I/ (v1,..., vs) = 0 then append the polynomial t - a^j to G where sj is the i-th element o/S. Delete all multiples o/t in L and continue with step (2).
(5) Now let (v1,..., vs) = 0. Append (v1,..., vs) as a new row to M, append t - a^j to S, append t to O, and append to L all elements o/the set {x1t,..., xnt, y1t,..., yet} which are not in L or in Lto (G). Then continue with step (2).
(6) Using row operations, trans/orm M into a diagonal matrix. Mimick these row operations on the elements o/S.
(7) Forj = 1,...,m, let/j = c^j where sj is the i-th element o/S. Return (/1,... ,/m) and G and stop.
This is an algorithm which computes a tuple o/polynomials (/1,... ,/m) ϵ Qm such that cj = /j(pi, Kj) /ori = 1,...,sandj = 1,...,m, as well as a set o/polynomials G c Qwhich is a o-Gröbner basis of the vanishing ideal
I(X) = {g ϵ Q | g(pt, Kj) = 0 /ori = 1,..., s}.
A proof of this theorem is contained in [KR2], Section 6.3. Given a cryptosystem whose encryption map we can apply to individual plaintext units and Keys, the BuchbergerMöller algorithm can be used to construct a polynomial map which correctly represents the encryption map for many (or even all) inputs. A further, common way to apply the theorem is to determine polynomial representations of S-Boxes in symmetric ciphers.
13.3.1 The Gröbner Basis Attack
Above we showed that breaking many types of cryptosystems can be reduced to solving large systems of polynomial equations over finite fields. For a long time, this had been considered an utterly impossible task. The situation changed when J.-C. Faugere broke the HFE Challenge in [Fau] using a Gröbner basis computation. Let us outline the general method.
Let K be a finite field, let P = K[x1,.. .,xn], and let f1, ·, fs ϵ P be polynomials defining a system of equations
/1(x1,...,x„) = 0
(S)
/s(x!,...,x„) = 0.
We form the polynomial ideal I = (/1,...,/s, -x1,..., xf -xn) where q = #K. Our task is to find the zero set
Z(I) = {(a1,..., an) ϵ Kn | /(a1,..., a„) = 0 for all/ ϵ I}.
To solve this task, it is sufficient to compute any Gröbner basis of the ideal I. Then there is an efficient algorithm, called the FGLM Algorithm (see [FGLM] or [DE], Section 2.2.4), to compute the reduced Gröbner basis of I with respect to the lexicographic term ordering o = Lex. Using a linear coordinate transformation, we can then bring I into normal xn-position, that is we can make sure that the last coordinates of the points of Z(I) are pairwise distinct (see [KR1], Section 3.7). Finally, we are in the setting of the Shape Lemma (cf. [KR1], Theorem 3.7.25) which says that the reduced Lex-Gröbner basis G of I has the following shape:
G = x - g!(x„), ..., x„_1 - g„_1(x„), g„(x„)}
By factoring gn(xn), it is then easy to read off its zeros, and substituting these into the other polynomials of G reveals the zeros of I.
Using the following remark, many of these steps can be simplified in practice.
Remark 13.3.6. When we carry out an algebraic attack and search for the secret Key, the polynomial system (S) has frequently a unique solution. In this case every reduced Gröbner basis G of I is of the form G = {x1 - a1,...,xn - an} where (a1,..., an) ϵ Kn is the unique solution of (S).
Our next example represents the first important case of a successful Gröbner basis attack.
Example 13.3.7. (The HFE Challenge). Let K be a finite field having q = 2” elements. The encryption function of the HFE cryptosystem can be described as a composition e = S°F°T : K —> K where S, T areinvertiblelinearmapsandF can be identified (via an identification P2n s Z2,) with a polynomial map/ : ^2 —> ^2 given by/(x1, ...,xn) = (q1(x1,..., xn),..., qn(x1,..., xn)) with quadratic polynomials qt €Z2 [x1,..., xn].
Then the secret Key of HFE is the triple (S, F, T) and the public Key is the tuple of polynomials (p1,... ,pn) with p; ϵ Z2[x1,.. .,xn] representing the encryption map S ° F ° T as above. To break this system, it is clearly sufficient to solve the set of polynomial equations pi(x1,..., xn) = c{ for i = 1,..., n, where c{ is the i-th bit of the ciphertext.
In [Fau], J.-C. Faugere carried out this Gröbner basis attack via an improved version of Buchberger’s Algorithm, called the F5-Algorithm, to break the first HFE Challenge with n = 80.
13.3.2 The Integer Programming Attack
In this subsection we will restrict our attention to algebraic attacks based on polynomial systems defined over Z2. Although the generalization to other finite base fields is straightforward, we want to concentrate on the fundamental principles in the most important case. The task of solving a polynomial system (S) withf1,..., fs €Z2 [x1,..., xn] can be rephrased as follows: Find a tuple (a1,..., σn) ϵ {0,1}n such that
F1(a1,...,an) = 0 (mod 2)
Fs(a1,...,an) = 0 (mod 2)
where Fj ϵ Z[x1,..., xn] is the canonical representative offj. Thus we are looking for an integer solution (a1,..., an) of this system which satisfies 0 < aj < 1. This formulation suggests to linearise the system and to apply an Integer Programming (IP) algorithm
for finding a solution satisfying the stated bounds. The following proposition turns this idea into an effective algorithm.
Proposition 13.3.8 (The Integer Programming Attack). Letf1,...,fs ϵ P = Z2[x1, ...,xn]. Then the following instructions define an algorithm which computes a tuple (a1,...,an) ϵ {0,1}n which defines a zero of the polynomial ideal I = (f1,... ,fm, xf +
x1,...,xf + xn}.
(1) Reduce f1,...,fs modulo the field equations, that is, make their terms squarefree. For i = 1,..., s, let T be the set of terms of degree > 2 in fj and sj the number of terms inf.
(2) For i = 1,..., s, introduce a new indeterminate Kj and write down the linear inequality Kj : Kj < Lsj/2J.
(3) For every tj ϵ Tj, introduce a new indeterminate yjj. For i = 1,..., s, write f = £;- tj +
I where the sum extends over all j such that tj ϵ Tj and where I, ϵ Ps1. Form the linear equation Fj: £;- yjj + I - 2 Kj = 0.
(4) For i ϵ {1,..., s} and tj ϵ Tj, write tj = x^ • • • x^ with 1 < j1 < · < jr < n. Form the linear inequalities Yjj: yjj - xj < 0 and Zjj : -yjj + x^ + · + x^ - r +1 < 0.
(5) For all i €{1,..., s}, letXj: xj < 1.
(6) Choose a linear polynomial c ϵ Q[x;-, yjj, Kj] and use an IP solver to find a tuple of natural numbers (ap bj, cj) which solves the system of linear equations and inequalities {K,, Fj, Yjj, Zjj, X} and minimizes C.
(7) Return (a1,...,an) and stop.
Proof. Since we are looking for natural numbers a¡ for which Xt holds, we have a¡ e {0,1}. Similarly, we have by e {0,1} by X¡ and Y¡_¡. Moreover, if t¡ e T¡ and if one of the numbers a;1,..., a¡ is zero then Yy implies by = 0. On the other hand, if a;1 = · = ajr = 1 then Z¡¡ implies by > 1. Altogether, this means that by equals aj • • • ajr, the value of t¡ at (a1,..., an).
Next it follows from F¡ that fi(a1,..., an) = 2 k¡ is an even number, and K¡ is nothing but the trivial bound for k¡ implied by the number of terms of f¡. In this way the solutions of the IP problem correspond uniquely to the tuples (a1,..., an) e {0,1}n which satisfy the above reformulation of the given polynomial system. □
In this proposition we have not taken any advantage of the possibility to choose the cost function C. Obviously, the number of additional indeterminates y¡¡ (and K¡)wehave to introduce depends on the sparsity of the system (S). For systems with few quadratic or higher degree terms, even a straightforward, non-optimized implementation yields satisfactory results, as our next example shows.
Example 13.3.9. Given the CTC (“Courtois Toy Cipher”) cryptosystem introduced in [Cou] and a plaintext-ciphertext pair, we construct an overdetermined algebraic system of equations in terms of the indeterminates representing Key bits and certain intermediate quantities. The task is to solve the system for the Key bits. The size of the system depends mainly on two parameters: the number b of simultaneous S-boxes and the number N of encryption rounds used.
For instance, in the case b = 3 and N = 4 we have to solve a polynomial system having 153 indeterminates, 285 equations, and 180 non-linear terms. Using a standard PC, the public domain IP solver GLPK, and the proposition, this system can be solved in less than a minute.
13.3.3 The SAT Attack
In this subsection we continue to work over the field K = Z2. In order to solve the polynomial system (S), we proceed as follows:
(1) Linearise the system by introducing a new indeterminate for each term occurring in one of the polynomials.
(2) Having written a polynomial as a sum of indeterminates, introduce new indeterminates to cut it after a certain number of terms. (This number is called the cutting number.)
(3) Convert the reduced sums into their logical equivalents using a CNF conversion.
Here CNF means conjunctive normal form and represents a set of propositional logic clauses of a certain type. Such sets of CNF clauses can be solved very efficiently using so-called SAT solvers. Therefore the transformation to a problem in logic is currently the fastest and most powerful way to solve polynomial systems over Z2.
To explain this technique in more detail, we start by elaborating the transformation of a polynomial equation into its logical equivalent. Let M = {X1,...,Xn} be a set of boolean variables (atomic formulas), and let M be the set of all (propositional) logical formulas that can be constructed from them, that is all formulas involving the operations -, A, and v.
Definition 13.3.10. Let f ϵ Z2[x1,.. .,xn]. A logical formula F ϵ M is called a logical representation of f if fyσ(f) = f(a1,..., an) + 1 for every σ = (a1,..., an) ϵ Zf. Here $σ denotes the boolean value of F at the tuple of boolean values σ where 1 = true and 0 = false.
The following lemma provides the central step for the logical conversion process.
Lemma 13.3.11. Letf ϵ Z2 [x1,..., xn, y] be of the form f = l1 ·ls + y, where 1 < s < n and I ϵ {•, xj + 1} for i = 1,..., s. We define formulas Lj = Xj if I = xj and Lj = -X if 1 = xj + 1. Then
F = (-Y v L1) A · A (-Y v Ls) A (Y v^L1 v · v -Ls)
is a logical representation off. Notice thatF is in conjunctive normal form (CNF) and has s +1 clauses.
Proof. Let σ = (a1,..., an, b) ϵ Zf+1. By induction on s, we show $σ(f) = f(a) + 1. In the case s = 1 we have f = x1 + y + c with c ϵ {0,1} and F = (-Y v L1) A (Y v -’L1) where L1 = X1 if c = 0 and L1 = -X1 if c = 1. The claim $σ(f) = f (a) + 1 follows easily with the help of a truth table.
Now we prove the inductive step, assuming that the claim has been shown for s -1 factors I, that is forf = l1 · ls-1 and the corresponding formula F’. To begin with, we assume that ls = xs and distinguish two sub-cases.
(1) If as = 0, we have $σ(f) = $σ(-Y v L1) A · A (-Y v Ls-1) a — = $b(-Y) and f (a) = b. This shows $σ(f) = f (a) + 1.
(2) If as = 1, we have f(a) = f(a). Using $σ(Ls) = 1, we obtain
$a(f) = 0a(-Y v L1) A · A (-Y v Ls_1) A (Y VL1 v^ • •v -.Ls_1) = $„(?)• Hence the inductive hypothesis yields $σ(f) = $σ(F’) = f(a) + 1 = f(a) + 1.
In the case ls = xs + 1, the proof proceeds in exactly the same way. □
Using this lemma, we define a standard conversion strategy for f ϵ Z2 [x1,..., xn] as follows. Choose a cutting number l> 3. For each non-linear term t appearing in f, introduce a new indeterminate y and a new boolean variable Y. Substitute y for t in f and append the clause corresponding to t + y in the lemma to the set of clauses.
After f has been linearised, choose a polynomial g consisting of <1-1 terms off, introduce a new indeterminate z, replace f by f - g + z and collect the polynomial g + z in a set L. Repeat this step until all of f has been cut to short sums of terms.
Finally, use the fact that the logical representation of g + z is -G o Z repeatedly to transform L into a set of CNF clauses.
Let us apply this transformation to an actual example polynomial.
Example 13.3.12. Let f = x1x2 + x2x3 + x1 + x2 + 1 ϵ Z2[x1,x2,x3]. We convert f into a set of CNF clauses as follows. First we let y1 = x1x2 and start with the corresponding clauses L = {-Y1 v X1, ->Y1 v X2, Y1 v ->X1 v -X2}. Then we set y2 = x2x3 and append the analogous three clauses to L.
Now we have f = y1 + y2 + x1 + x2 + 1 and choose I = 3. Lettingg1 = z1 + y1 + y2, we have corresponding clauses G1 = {-Z1 v Y1 v Y2, Z1 v->Y1 v Y2, Z1 v Y1 v->Y2, -Z1 v-iY1 v-iY2}. Similarly, the polynomials g2 = z2 + x1 + x2 leads to a set of four clauses G2 and f = z1 + z2 + 1 corresponds to F = {-Z1v2, Z1 v ->Z2}.
Altogether, the standard CNF conversion of f consists of the 16 clauses in L u G1 u G2 u F.
The application of state-of-the-art SAT solvers now allows us to solve very big polynomial systems arising from algebraic attacks. Here is a case in point.
Example 13.3.13. In the CTC family of cryptosystems (see [Cou]), we choose b = 6 simultaneous SBoxes and N = 6 encryption rounds. A straightforward algebraic attack yields a polynomial system consisting of 612 quadratic equations in 468 indetermi- nates over the field Z2. The above transformation strategy converts this system to a set of 5065 propositional logical clauses in 937 boolean variables. Standard SAT solvers such as CryptoMiniSat solve this SAT instance in a few seconds on a standard PC.
With this example we end our excursion into algebraic attacks. For the interested reader, we suggest to consult [Kre] for further variants.
13.4 Exercises
13.1 Prove that the orderings <lex and <drl defined in Example 13.1.3 are indeed term orderings.
13.2 Define an ordering relation <rlex on Tn by letting t = x”1 ·x”“ <rlex t = x11 ·x”“ if and only if the last non-zero component of (a1 - fi1,...,an - fin) is negative. Show that this reverse lexicographic ordering is a multiplicative ordering relation, but not a well-ordering. How are the indeterminates ordered by <rlex?
13.3 Let σ be a term ordering on Tn, and let f ϵ K[x1, ...,xn] {0}. Prove that the leading term ideal of the principal ideal f} is generated by Ltσ f).
13.4 Using the term ordering σ = drl, show that the following sets of polynomials are σ-Gröbner bases of the ideals they generate.
(a) G1 = {x2 - 1, xy - 1, x - y, y2 - 1} in K[x, y] (see Example 13.1.9)
(b) G2 = {y2 - x, z3 - x} in K[x, y, z]
(c) G3 = {x2 - y2, xy2 - z3, y4 - xz3} in K[x,y,z]
13.5 Generalize Example 13.2.1 to a Graph-p-Colouring Cryptosystem, wherep > 2 is a prime. Describe a suitable polynomial ring and the polynomials which form Alice’s public Key.
13.6 Let K be a field which contains three solutions of x3 = 1, i.e., three cubic roots of unity. Suppose that these cubic roots of unity represent three colours. Define a suitable ideal in a polynomial ring K[x1, ...,xn] such that 3-colourings of a graph r = (V, E) correspond uniquely to zeros of this ideal.
13.7 Given a graph r = (V, E), a perfect code in r is a subset S c V such that every vertex of r is in S or joined to precisely one element of S by an edge. For every v ϵ V, let Nv be the neighbourhood of v, i.e., the set consisting of v and all vertices of r which are joined to v by an edge. The problem of finding a perfect code in r is Known to be NP-complete.
(a) Let V = {v1,..., vr}, andletP = Z2[x1 ,...,xn]. For i = 1,..., r,welet fj = 1 - Z;eN x;-,andifdistr(v;-, vk) < 2, we letgjk = xjxk. Show that the polynomials f gjk generate an ideal whose zeros correspond uniquely to perfect codes inr.
(b) Using (a), construct an instance of the Polly Cracker Cryptosystem whose security depends on the Graph Perfect Code search problem in r.
13.8 Suppose that Alice and Bob are using the RSA cryptosystem with the public Keys n = 77 and e = 11, and the secret Key d = 11. We represent an element c0 + 2c1 + 4c2 + 8c3 + 16c4 + 32c5 + 64c6 in Z77 with cj ϵ {0,1} by the tuple (co,...,c6)inZf.
(a) Compute polynomials in Z2[x0,...,x6] which represent the encryption map e : —> Zf.
(b) Decrypt the ciphertext (0,1,1,1,0,1,0) by solving the corresponding polynomial system via a Gröbner basis calculation.
