5 Elementary Number Theoretic Techniques

5.1    Cryptography and Number Theory

Number theory plays a prominent role in many areas of cryptography. In the simplest case of applying a cryptosystem to an N letter alphabet, as explained in Chapter 1, we consider the letters as integers modulo N. The integers modulo N form a ring called the modular ring, _N, and hence encryption is done within this ring. Operations within the various modular rings are called modular arithmetic. The encryption algorithms then apply number theoretic functions and use modular arithmetic on these integers. It follows that encryption maps on k-length-message units are functions

In addition to providing a framework for the encrypted alphabets, number theoretic problems provide the security in the basic public key protocols. Recall from the last chapter that the security of a cryptographic protocol is usually based on the difficulty of solving some “hard” problem. For example in the Diffie-Hellman method, one of the main techniques in public key cryptography, the hard problem is the discrete log problem. We will discuss the discrete log problem and some attempted solutions in Chapter 6. The discrete log problem was used in one of our zero-knowledge proof examples (see Section 4.6). The other most commonly used public key method, the RSA method, is based on the factorization problem. The factorization problem is the relative difficulty of factoring large integers. This will be discussed also in Chapter 6.

In the next two chapters we introduce and discuss all the relevant material from number theory and related abstract algebra, especially finite group theory, that will be necessary for cryptographic applications. For more material and more complete discussions on these mathematical area see the book [FR]. For further references on abstract algebra we refer to [CFR1] or [FGR].

We first discuss modular arithmetic.

5.2    Modular Arithmetic

For each natural number n, we will construct a ring, called the ring of integers modulo n, which we will denote by _n, and which will be finite with n elements. Each of these rings will be a commutative ring with an identity. Collectively the rings are called the modular rings and operations within these rings are called modular arithmetic. We assume that the reader has a basic familiarity with primes, divisibility, the fundamental theorem of arithmetic and the concepts of a greatest common divisor or gcd and a least common multiple or lcm. Given integers a, b we denote their gcd by (a, b). If (a, b) = 1 then the integers a, b are relatively prime or coprime. For more information on basic number theory we refer to [FR].

Given n ≥ 1, in order to construct the ring _n we must first introduce the relation of congruence modulo n on the integers .

Definition 5.2.1. Suppose that n ≥ 1 is a positive integer. If x,y are integers such that x − y is a multiple of n or equivalently that n divides x − y we say that x is congruent to y modulo n and denote this by x ≡ y (mod n). If n does not divide x − y then x and y are incongruent modulo n.

If x ≡ y (mod n),then y iscalleda residue of x modulo n.Given x ∈ the set of integers

is called the residue class for x modulo n. We denote this by [x]. Notice that x ≡ 0 (mod n) is equivalent to x being a multiple of n. We first show that the residue classes partition , that is that each integer falls in one and only one residue class.

Theorem 5.2.2. Given n ≥ 1, an integer, then congruence modulo n is an equivalence relation on the integers. Therefore the residue classes partition the integers.

Proof. Recall that a relation ~ on a set S is an equivalence relation if it is reflexive, that is s ~ s for all s ∈ S; symmetric, that is if s₁ ~ s₂ then s₂ ~ s₁ and transitive, that is if s₁ ~ s₂ and s₂ ~ s₃, then s₁ ~ s₃. If ~ is an equivalence relation then the equivalence classes [s] = {s є S | s₁ ~ s} partition S.

We recall the notation m | n indicates that m divides n, so that m ≡ nk for some integer k. Consider ≡ (mod n) on . Given x є , x − x ≡ 0 ≡ 0 n so n | (x − x) and so x ≡ x (mod n). Therefore ≡ (mod n) is reflexive.

Suppose that x ≡ y (mod n). Then

for some a є . Then y − x = −an so n | (y − x) and so y ≡ x (mod n). Therefore the relation ≡ (mod n )is symmetric.

Finally, suppose that x ≡ y (mod n) and y ≡ z (mod n). Then x − y = a_xn and y − z = a₂n. But then x − z = (x − y) + (y − z) = a₁n + a₂n = (a₁ + a₂)n. Therefore n | (x − z) and x ≡ z (mod n). Therefore ≡ (mod n) is transitive and the theorem is proved.

Hence given n > 0 every integer falls into one and only one residue class. We now show that there are exactly n residue classes modulo n.

Theorem 5.2.3. Given an integer n > 0 there exist exactly n residue classes. In particular, [0], [1],…, [n − 1] gives a complete set of residue classes.

Proof. Given x є , x must be congruent modulo n to one of 0,1,2,…, n − 1 since the remainder when we divide x by n is less than n. Further these are all incongruent modulo n. As a consequence

gives a complete set of residue classes modulo n and hence there are n of them. □

Recall that a ring and a field are defined as follows (see [CFR1]).

Definition 5.2.4. A ring is a set R with two binary operations defined on it. These are usually called addition, denoted by +, and multiplication denoted by · or just by juxtaposition, satisfying the following six axioms:

(1)  Addition is commutative: a + b = b + a for all a, b є R.

(2)  Addition is associative: a + (b + c) = (a + b) + c for a, b, c є R.

(3)  There exists an additive identity, denoted by Osuch that a + 0 = a for each a є R.

(4)  For each a є R there exists an additive inverse denoted by -a such that

(5)  Multiplication is associative: a(bc) = (ab)c for a, b, c є R.

(6)  Multiplication is left and right distributive over addition:

for a, b, c є R.

(7)  If in addition multiplication is commutative: ab = ba for all a, b in R, then R is a commutative ring.

(8)  Further if there exists an multiplicative identity denoted by 1 such that a · 1 = a and 1 · a = a for each a in R then R is a ring with identity or a ring with unity if R satisfies (1) through (6) and (8).

(9)  If R satisfies (1) through (8) then R is a commutative ring with an identity or with a unity.

Finally, a field F is a commutative ring with an identity such that each non-zero element of F has a multiplicative inverse. That is, if x є F with x ≠ 0 then there exists an x₁ є F such that xx₁ = 1.

We now construct the ring _n on the set {[0], [1],…, [n − 1]} of residue classes modulo n. We first need the following whose proof is straightforward.

Lemma 5.2.5. If a ≡ b (mod n) and c ≡ d (mod n), then

(1)  a + c ≡ b + d (mod n),

(2)  ac ≡ bd (mod n).

We now define operations on the set of residue classes.

Definition 5.2.6. Consider the complete residue system {[0],…, [n − 1]} modulo n. On this set of residue classes define

(1)   [x_i] + [x_j] = [x_i + x_j],

(2)  [x_i][x_i] = [x_ix_j].

From this we get the following result. The proof is a direct verification of the ring axioms.

Theorem 5.2.7. Given a positive integer n ≥ 1, the set of residue classes

{[0],…, [n − 1]}

forms a commutative ring with an identity under the operations defined above. This is called the ring of integers modulo n and is denoted by _n. The zero element is [0] and the identity element is [1].

We usually consider _n as consisting of 0,1,…, n − 1 with addition and multiplication modulo n. For an integer a we will denote the residue class for a and hence the element of _n by ā. When there is no confusion we will denote the element ā in _n as just a. We emphasize, however, that even though we are denoting the elements of _n by 0,1, 2,…, n - 1, they are still residue classes or equivalence classes. This is just to simplify our notation. Below we give the addition and multiplication tables modulo 5, that is in ₅. We note that, in line with the comment that these elements are different from usual integers. Consider 3 + 4 and 3 • 4. They are both equal to 2 in Z₅. This is certainly not what happens if we add and multiply 3 and 4 in .

Example 5.2.8. Addition and Multiplication Tables for Z₅

Notice for example that modulo 5, 3 · 4 = 12 ≡ 2 (mod5) so that in ₅, 3 · 4 = 2. Similarly 4+2 = 6 ≡ 1 (mod5) soin ₅,4 + 2 = 1.

5.3    Units and the Multiplicative Group

In a commutative ring with an identity,(like each of the modular rings _n) a unit is an element that has a multiplicative inverse. For example in the integers only 1 and −1 are units. On the other hand, in a field, such as the rationals, by definition, every non-zero element is a unit. The set of units in such a ring always is non-empty since the multiplicative identity is a unit. We denote the set of units in a ring R by U(R).

Recall next that a group G is a set with one binary operation that we denote by · or just by juxtaposition, defined on it, satisfying the following three axioms:

(1)  The operation is associative. That is, we have g₁(g₂g₃) = (g₁g₂)g₃ for all g₁,g₂, g₃ є G.

(2)  There is an identity, denoted 1, for the operation. Hence for each g є G we have 1g = g1 = g.

(3)  Each g є G has a inverse. That is there exists a g⁻¹ for each g such that gg^-−1 = g⁻¹g = 1.

If the operation is also commutative then G is called an abelian group. The additive part of any ring is an abelian group and hence the additive parts of all the modular rings are finite abelian groups.

We need that the set of units in a commutative ring forms an abelian group.

Lemma 5.3.1. For a commutative ring R with identity the set of units U(R) forms an abelian group under the ring multiplication. We call this the unit group ofR.

We usually denote the unit group in a ring R by R*. Hence will denote the unit group in the modular ring _n. Given an integer a it is easy to determine if ā, the residue class of a modulo n, is a unit and hence is in . This will be true if and only if a is relatively prime to n. Recall that the gcd of two integers a, b can be expressed as a linear combination of them. Further, a and b are relatively prime if and only if 1 is expressible as a linear combination of a and b.

Lemma 5.3.2. Ifn > 1 and a є then ā is a unit in if and only if (a, n) = 1.

Proof. Suppose (a, n) = 1. Then there exists x, y є such that ax + ny = 1. This implies that ax = 1 (mod n) which in turn implies that = 1 in and therefore a is aunit.

Conversely, suppose that a is a unit in . Then there is an x є with ax = 1. In terms of congruence then

Therefore 1 is a linear combination of a and n and so (a, n) = 1. □

The next result, called the Euclidean algorithm, provides a technique for both finding the gcd of two integers and expressing the gcd as a linear combination of the two integers. If an element a є _n is aunit this will also provide a method to find its inverse in _n.

Theorem 5.3.3 (The Euclidean Algorithm). Given integers band a > 0 form the repeated divisions

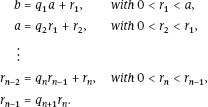
The last non-zero remainder r_n is the gcd of a, b. Further r_n can be expressed as a linear combination of a and b by successively eliminating the r_i’s in the intermediate equations.

Example 5.3.4. Find the gcd of 270 and 2412 and express it as a linear combination of 270 and 2412.

We apply the Euclidean algorithm

Therefore the last non-zero remainder is 18 which is the gcd. We now must express 18 as a linear combination of 270 and 2412.

From the first equation

which gives in the second equation

which is the desired linear combination.

The following lemma whose proof can be found in [FR] provides a technique to find the lcm of two integers. If a, b are two integers we denote their least common multiple by lcm(a, b) or [a, b].

Lemma 5.3.5. If a, b єZ then (a, b)[a, b] = ab.

Example 5.3.6. Find the lcm of 270 and 2412.

From the previous example we found that gcd(270,2412) = 18. Therefore lcm(2 7 0, 24 1 2) = ⁽²⁷⁰⁾12⁴¹²⁾ = 36 180.

The same method can be applied to finding the inverse of a unit and to solve linear equations in a modular ring. Recall from Chapter 1 that a decryption of an affine cipher requires solving a linear equation in a modular ring.

Example 5.3.7. Find the multiplicative inverse of 5 in Z₁₇.

Notice that ₁₇ is a field so every non-zero element is a unit. Now (5,17) = 1 so we use the Euclidean algorithm to express 1 as a linear combination of 5 and 17. We get

Considering these in ₁₇ and using that 17 = 0weget

Hence is the inverse of in ₁₇.

If a is a unit in Z_n then a linear equation

can always be solved with a unique solution given by x = a^-1(c - b).

Example 5.3.8. Solve 5x + 4 = 2 in Z₆.

Since (5, 6) = 1 it follows that 5 is a unit in Z₆. Therefore x = 5^-1(2 - 4). Now 2 - 4 = -2 = 4 in Z₆. Further 5 = -1so 5^-1 = -1^-1 = -1. Then we have

Thus the unique solution in ₆ is x = 2.

Since an element ā is a unit in _n if and only if (a, n) = 1 it follows that the number of units in _n is equal to the number of positive integers less than or equal to n and relatively prime to n. This number is given by what is called the Euler Phi Function.

Definition 5.3.9. For any n > 0,

ϕ (n) = number of positive integers less than or equal to n and relatively prime to n.

Example 5.3.10. ϕ (6) = 2 since among 1,2,3,4,5, 6 only 1,5 are relatively prime to 6.

The following is immediate from our characterization of units.

Lemma 5.3.11. The number of units in Z_n, which is the order of the unit group U(Z_n), is $ (n).

Definition 5.3.12. Given n > 0 a reduced residue system modulo n is a set of integers x₁,…, x_k such that each x_{ is relatively prime to n, x_{ = xj modulo n unless i = j and if (x, n) = 1 for some integer x then x = x_{ (mod n) for some i.

Hence a reduced residue system is a complete collection of representatives of those residue classes of integers relatively prime to n. Hence it is a complete collection of units (up to congruence modulo n) in _n. It follows that any reduced residue system modulo n has $ (n) elements.

Example 5.3.13. A reduced residue system modulo 6 would be {1, 5}.

We now develop a formula for $ (n). We first determine a formula for prime powers and then paste back together via the fundamental theorem of arithmetic to develop our general formula.

Lemma 5.3.14. For any prime p and m > 0,

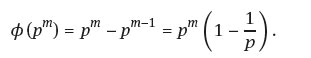
Proof. The numbers a, 1 < a < p^e with (a, p^e) > 1 are precisely the multiples of p, that is

All the others are relatively prime to p^e. Therefore $ (p^e) = p^e - p^e-1.

The following lemma says that the Euler Phi Function is a multiplicative function. For a proof of this lemma we refer to [FR].

Lemma 5.3.15. If (a, b) = 1 then $ (ab) = $ (a) $ (b).

Based on this lemma and the fundamental theorem of arithmetic we get the general formula for $ (n).

Theorem 5.3.16. Suppose where thep_{ are distinct primes, then

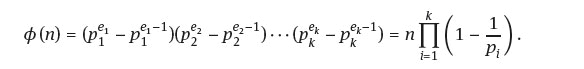
Proof. From the previous Lemmas we have since gcdp, pj’) = 1 for i = j

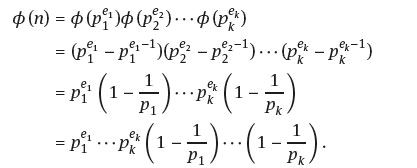
Example 5.3.17. Determine ϕ (126). Now

Hence there are 36 units in Z₁₂₆.

5.4    The Field and Finite Fields

In the previous section we saw that an element a in the modular ring _n is a unit if and only if (a, n) = 1. If n = p with p a prime then every integer except multiples of p are relatively prime to p and therefore become units in Z_p. The multiples of the prime p correspond to the zero element of Z_p and hence it follows that every non-zero element of Z_p is a unit. Recall that a field is a commutative ring with an identity where every non-zero element is a unit. Since for any natural number n the modular ring Z_n is a commutative ring with an identity it follows that if p is a prime then Z_p is a field. This proves the first part of the following theorem.

Theorem 5.4.1. The modular ring Z_n is a field if and only if n = p is a prime. For the field _p the non-zero elements form a group, namely the unit group.

Proof. If p is a prime then as explained above Z_p forms a field.

Conversely, suppose that _n is a field. First recall that a field must be an integral domain, that is there can be no zero divisors, that is no non-zero elements a, b with ab = 0. Now suppose that n is not prime so that n = mk with 1 < m, k < n. Then neither m nor k are 0 in _n but mk = 0 in _n. Hence _n has zero divisors which cannot occur in a field. Therefore n must be prime. □

Hence for each prime p we have a finite field _p. We next show that if F is any finite field, that is a field with finitely many elements, then F must have size pⁿ for some prime p and natural number n. Further given a prime power pⁿ there exists a unique field (up to isomorphism) of order pⁿ. We call this unique field GF(pⁿ) denoting the Galois field of order pⁿ. We also denote this by F = _q, q = pⁿ. Finite fields are used quite often in cryptography. In the AES and DES symmetric key systems computations are done in the Galois fields GF(2ⁿ).

Theorem 5.4.2. Any finite field F has size pⁿ for some prime p and natural number n.

Proof. Let F be a finite field. If its characteristic were 0 then F would be infinite and its characteristic (see [CFR1]) must be a prime p. It follows that F is a finite dimensional vector space over the finite field Z_p. Suppose that v₁,…,v_n is a finite basis. Then every element of F can be written uniquely as a linear combination

Since there are p choices for each c_{ there arepⁿ choices for these linear combinations.

A proof of the following theorem can be found in [CFR1].

Theorem 5.4.3. Given a prime p a and natural number n there exists a unique (up to isomorphism) field of size pⁿ.

As noted above this unique field is denoted by GF(pⁿ) or by _q with q = pⁿ.

We close this subsection with several other results in elementary number theory involving primes that appear in cryptography. The first is called Fermat’s Theorem.

Theorem 5.4.4 (Fermat). Letp be a prime. Then

for each a єZ, that is p(a^p - a). Hence in the ring Z_p we have a^p = a and if a = 0 then a^p-1 = 1.

Proof. Here we give a purely number theoretic proof. In the next section we give a proof based on elementary group theory. If a = 0 (mod p) then a^p = 0 (mod p) so a^p = a (mod p).

If a = 0 (modp) so that (a,p) = 1, let {r₁,…, r_p} be a complete residue system modulo p with r_p = 0. Since (a,p) = 1 then {ar₁, ar₂,…, ar_p} is also a complete residue system modulo p and ar_p = 0 (modp). Then we have

However, (r₁ … r_p-1) is not divisible by p so it is a unit in Z_p and hence we can divide through by it to get the result;

Theorem 5.4.5 (Wilson). Letp be aprime. Then

Conversely if (p - 1)! = −1 (modp) thenpis aprime.

Proof. Now (p - 1)! = (p - 1)(p - 2) ••• 1. Since Z_p is a field each

has a multiplicative inverse modulo p. Further suppose x = x^-1 in Z_p. Then x² = 1 which implies (x - 1)(x + 1) = 0 in Z_p and hence either x =1or x = −1 since Z_p is an integral domain. Therefore in Z_p only 1, −1 are their own multiplicative inverses. Further −1 = p - 1 since p - 1 = −1 (modp).

Hence in the product (p - 1)(p - 2) … 1 considered in the field Z_p each element is paired up with its distinct multiplicative inverse except 1 and p−1. Further the product of each with its inverse is 1. Therefore in Z_p we have (p - 1)(p - 2) … 1 = p −1. Written as a congruence then

Conversely suppose (n - 1)! = −1 (mod n). If n were composite then n = mk with 1 < m < n - 1 and 1 < k < n - 1. Hence, if m = k then both m and k are included in (n −1)!. It follows that (n −1)! is divisible by n so that (n −1)! = 0 (mod n) contradicting the assertion that (n - 1)! = −1 (mod n). If m = k then n = m².If m = 2 then n = 4 and (n - 1)! = 2 (mod 4) contradicting the assertion (n - 1)! = −1 (mod 4).

If m > 3 then (n - 1)! = 0 (mod m) but −1 = 0 (mod m).

Therefore n must be prime. □

5.5    Finite Abelian Groups

The modular rings _n form finite abelian groups under addition, while their unit groups U(_n) form finite abelian groups under multiplication. Here we discuss some important results from finite group theory that are applicable to both number theory and cryptography.

Recall that the number of elements in a finite group G is called the order of G denoted |G|. Each element in a group G generates a subgroup called the cyclic subgroup generated by g. This consists of the powers of the element g. The cyclic subgroup generated by g is denoted (g) and the order of this subgroup is called the order of g. We will denote the order of an element g є G by o(g) or 〈g〉. The first result called Lagrange’s Theorem restricts the order of subgroups. For proofs of the results in this section we refer the reader to the book [CFR1].

Theorem 5.5.1 (Lagrange’s Theorem). Let Gbea finite group of order n. Then the order of any subgroup divides n. In particular, the order of any element divides n and moreover gⁿ = 1 for each g є G.

Lagrange’s theorem provides an alternative proof of Fermat’s Theorem and an extension of it called Euler’s Theorem.

Consider a unit a єZ_n. Then a є U(Z_n) and hence a has a multiplicative order, that is there is an integer m with a^m = 1 in Z_n. In terms of congruences this means that a^m = 1 (mod n). If a єZ_n is not a unit then there cannot exist a power m > 1 such that a^m = 1 (mod n), if such an m existed then a^m-1 would be an inverse for a. The unit group U(Z_n) is a finite group of order $ (n) where $ is the Euler phi-function. Applying Lagrange’s Theorem to the group U(Z_n) we get the following result, known as Euler’s Theorem, which is an extension of Fermat’s Theorem.

Theorem 5.5.2 (Euler’s Theorem). If (a, n) = 1 then

If p is a prime $ (p) = p - 1 so applying Euler’s Theorem to the modular fields Z_p we recover as a corollary Fermat’s Theorem.

Corollary 5.5.3 (Fermat). If a єZ_p and a = 0 then a^p-1 = 1 (modp).

In general for finite abelian groups we have the following. Recall that a finite group G is the direct product

of subgroups H₁,…, H_k if

(1)  each g є G can be written uniquely in the form g = h₁ h₂ ••• h_k with h є H_{ for i = 1,…, k (unique up to the ordering of the factors);

(2)   hjhj = hjhj for h_t є H_;, hj є Hj if i = j.

Theorem 5.5.4. Let G be a finite abelian group with |G| = n then

(1)  if g₁, g₂ є Gwith g₁| = a, |g₂ | = b then (g₁g₂)^lcm(a’^b) = 1;

(2)  if g1, g2 є G with |g1| = a, g | = b and (a, b) = 1 then |g₁g₂| = ab;

(3)  ifn = p1¹ pj •••p^e_k is the prime factorization ofn then

where |H_i| = p^e_iⁱ.

Corollary 5.5.5. Let G be a finite abelian group and let H₁,…, H_k be subgroups of G with pairwise relatively prime orders |H_t|. Suppose that |G| = |H₁| |H₂| … |H_k|. Then G = H₁ × … × H_k.

5.6    Cyclic Groups and Primitive Elements

It follows from Euler’s Theorem that any unit a in Z_n has finite multiplicative order. For a є _n we denote this order by o(a) and further this natural number divides $ (n). The order of a is the order of the cyclic multiplicative subgroup of U(Z_n) generated by a. If (a, n) = 1 and the order of a is exactly $ (n) then a is called a primitive element modulo n. In this case the unit group is cyclic with a as a generator. We will prove that for n = p a prime there is always a primitive element. First we review some material about cyclic groups.

Recall that a cyclic group G is a group with a single generator g. G then consists of all the powers of g, that is G = {1, g^±1, g^±2,…}. If G is finite of order n then gⁿ = 1 and n is the least positive integer x such that g = 1. It is then clear that if g^m = 1 for some power m it must follow that m = 0 (mod n), and if g^k = g^l then k = l (mod n).

Let H = (Z_n, +) denote the additive subgroup of Z_n. Then H is cyclic of order n with generator 1. If G = (g) is also cyclic of order n then since multiplication of group elements is done via addition of exponents it is fairly straightforward that the homomorphism f : G ^ (Z_n, +) given by g ^ 1 is actually an isomorphism (see Chapter 9 for a formal definition of homomorphism and isomorphism and see the exercises). Further if G = (g) is cyclic of infinite order then g ^ 1 gives an isomorphism from G to the additive group of Z.

Lemma 5.6.1. Let G be a cyclic group,

(1)  If G is finite oforder n then G is isomorphic to (Z_n, +). In particular, all finite cyclic groups of a given order are isomorphic.

(2)  If G is an infinite cyclic group then G is isomorphic to (Z, +).

Cyclic groups are abelian and hence their subgroups are also abelian. However, as an almost direct consequence of the division algorithm we get that any subgroup of a cyclic group must also be cyclic.

Lemma 5.6.2. Let Gbea cyclic group. Then any subgroup ofG is also cyclic.

Proof. Suppose G = (g) and H c G is a subgroup. Since G consists of powers of g, H also consists of certain powers of g. Let k be the least positive integer such that g^k є H. We show that H = (g^k) that is H is the cyclic subgroup generated by g^k. This is clearly equivalent to showing that every h є H must be a power of g^k.

Suppose g^t є H. We may assume that t > 0 and that t > k since k is the least positive integer such that g^k є H.If t < 0 work with -t. By the division algorithm we then have

If r ≠ 0 then 0 < r < k and r = t-k. Hence g^r = g^t-k = g^tg^-k.Now g^t є Handg^k є Hand since H isa subgroup it follows that g^t-k є H. But then g є H which is a contradiction since 0 < r < k and k is the least power of g in H. Therefore r = 0 and t = qk. We then have

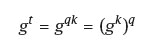
completing the proof.

Each element of a cyclic group G generates its own cyclic subgroup. The question is when does this cyclic subgroup coincide with all of G. In particular, which powers g^k are generators of G. The answer is purely number theoretic.

Lemma 5.6.3. Let G be a cyclic group.

(1)  Let G = (g) be a finite cyclic group of order n. Then g^k with k > 0 isa generator of G if and only if (k, n) = 1, that is k and n are relatively prime.

(2)  IfG = (g) is an infinite cyclic group then g, g^-1 are the only generators.

Proof. Suppose first that G = (g) is finite cyclic of order n and suppose that (k, n) = 1. Then there exists integers x, y such that kx + ny =1. It follows then that

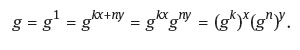
But gⁿ = 1 so (gⁿ)^y = 1 and therefore

Therefore g is a power of g^k and hence every power of g is also a power of g^k. The whole group g then consists of powers of g^k and hence g^k is a generator for G.

Conversely, suppose that g^k is also a generator for G. Then there exists a power x such that g = (g^k)^x = g^kx. Hence kx = 1 (mod n) and so k is a unit modulo n which implies from the last section that (k, n) = 1.

Suppose next that G = (g) is infinite cyclic. Then there is no power of g which is the identity. Suppose g^k is also a generator with k > 1. Then there exists a power x such that g = (g^k)^x = g^kx. But this implies that g^kx-1 = 1 contradicting that no power of g is the identity. Hence k =1. □

Recall that the Euler phi function ϕ (n) is equal to the number of positive integers less than n which are relatively prime to n. This is then the number of generators of a cyclic group of order n.

Corollary 5.6.4. Let Gbea finite cyclic group of order n. Then there are $ (n) generators for G.

By Lagrange’s Theorem, for any finite group, the order of a subgroup divides the order of a group, that is if |G| = n and |H| = d with H a subgroup of G then d|n. However, the converse in general is not true, that is if |G| = n and d|n there need not be a subgroup of order d. Further if there is a subgroup of order d, there may or may not be other subgroups of order d. For a finite cyclic group G of order n however, there is, for each d|n, a unique subgroup of order d.

Theorem 5.6.5. Let Gbe a finite cyclic group of order n. Then for each d|n with d > 1 there exists a unique subgroup H of order d.

Proof. Let G = (g) and |G| = n. Suppose d|n, then n = kd. Consider the element g^k. Then (g^k)^d = g^kd = g” = 1. Further if 0 < t < d then 0 < kt < kd so kt £ 0 (mod n) and hence g^kt = (g^k)^t = 1. Therefore d is the least power of g^k which is the identity and hence g^k has order d and generates a cyclic subgroup of order d. We must show that this is unique.

Suppose H = (g^t) is another cyclic subgroup of order d (recall that all subgroups of G are also cyclic). We may assume that t > 0 and we show that g^t is a power of g^k and hence the subgroups coincide.

Since H has order d we have g^td = 1 which implies that td = 0 (mod n). Since n = kd it follows that t > k. Apply the division algorithm

If r ≠ 0 then 0 < r < k and r = t - qk. Then

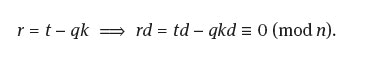
Hence n | rd which is impossible since rd < kd = n. Therefore r =0 and t = qk. From this

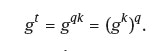
Therefore g^t is a power of g^k and H = (g^k). □

From this result we get the following concerning the Euler Phi Function.

Theorem 5.6.6. Forn > 1 and ford > 1

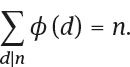
Proof. Consider a cyclic group G of order n. For each d , d > 1 there is a unique cyclic subgroup H of order d. H then has $ (d) generators. Each element in G generates its own cyclic subgroup H₁, say of order d and hence must be included in the $ (d) generators of H₁. Therefore

But this must be the whole group and hence this sum is n. □

We now return to primitive elements in the modular rings.

Theorem 5.6.7. For a prime p there is always an element a of order $ (p) = p - 1, that is a primitive element. Equivalently the unit group of Z_p is always cyclic.

Since every non-zero element in Z_p is a unit, the unit group U(Z_p) is precisely the multiplicative group of the field Z_p. The fact that U(X_p) is cyclic follows from the following more general result, which also shows that the multiplicative group of any finite field is cyclic.

Theorem 5.6.8. Let F be a field. Then any finite subgroup of the multiplicative group of F must be cyclic.

Proof. Suppose G c F is a finite multiplicative subgroup of the multiplicative group of F. Suppose G = n. As has been our general mode of approaching results we will prove it for n a power of a prime and then paste the result together via the fundamental theorem of arithmetic.

Suppose n = p^k for some k. Then the order of any element in G is p^a with a < k. Suppose the maximal order is p^t with t < k. Then the lcm of the orders is p^t. It follows that for every g є G we have g^pt = 1. Therefore every g є G is a root of the polynomial equation

However, over a field, a polynomial cannot have more roots than its degree. Since G has n = p^k elements and p^t < p^k this is a contradiction. Therefore the maximal order must be p^k = n. Therefore G has an element of order n = p^k and hence this element generates G and G must be cyclic.

We now do an induction on the number of distinct prime factors in n = |G|. The above argument handles the case where there is only one distinct prime factor. Assume the result is true if the order of G has less than k distinct prime factors. Suppose . Then n = p^ec where c has less than k distinct prime factors. Since G is a finite abelian group with

By the inductive hypothesis H and K are both cyclic so H has an element h of order p^e and K has an element k of order c. Since (p^e, c) = 1 the element hk has order p^ec = n completing the proof. □

Corollary 5.6.9. The multiplicative group of any finite field is cyclic.

This fact will play a role in the implementation of the Diffie-Hellman protocol (see Chapter 6).

Example 5.6.10. Determine a primitive element modulo 7.

This is equivalent to finding a generator for the multiplicative group of Z₇. The non-zero elements are 0,1,2,3,4,5,6 and we are looking for an element of order 6.

The table below list these elements and their orders

Therefore there are 2 primitive roots 3 and 5 modulo 7. To see how these were determined powers were taken modulo 7 until a value of 1 was obtained. For example

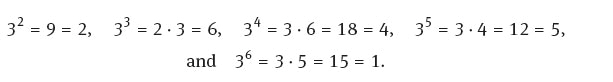
Example 5.6.11. Show that there is no primitive element modulo 15.

The units in Z₁₅ are {1,2,4, 7,8,11,13,14}. Since $ (15) = 8 we must show that there is no element of order 8. The table below gives the units and their respective orders

Therefore there is no element of order 8.

We have the following result which determines when there exists a primitive element in . A proof can be found in [FR].

Theorem 5.6.12. There is a primitive element for Z_n ifandonlyifn = 2,4, p, 2p, pⁿ for some odd prime p.

5.7    The Chinese Remainder Theorem

Systems of linear congruences are handled by the next result which is called the Chinese Remainder Theorem. This will also provide an important result describing the structure of the modular rings.

Theorem 5.7.1 (Chinese Remainder Theorem). Suppose that m₁, m₂,…,m_k are k positive integers that are relatively prime in pairs. If a₁,…,a_k are any integers then the simultaneous congruences

have a common solution which is unique modulo m₁m₂ … m_k.

Proof. The proof we give not only provides a verification but also provides a technique for finding the common solution.

Let m = m₁m₂ … m_k. Since them _i are relatively prime in pairs we have . Therefore there is a solution x_i to the reduced congruence

Further for x_i we clearly have

Now let

We claim that x₀ is a solution to the simultaneous congruences and that it is unique modulo m.

Now

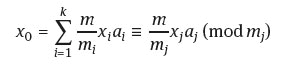
since (mod mj) if i ≠ j. It follows then that

since (mod mj). Thereforex₀ is a common solution. We must show the uniqueness part.

If x₀ is another common solution then x₀ = x₀ (mod ) for i = 1,…, k. Therefore x₀ = x₀ (mod m).

We note that if the integers m_{ are not relatively prime in pairs there may be no solution to the simultaneous congruences. □

Example 5.7.2. Solve the simultaneous congruences

Here m₁ = 13, m₂ = 45, m₃ = 17 so m = 13 ■ 45 ■ 17. We first solve

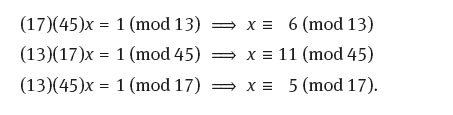
To see how these solutions are found lets look at the second one:

since 221 ≡ 41 (mod 45). We now use the Euclidean algorithm,

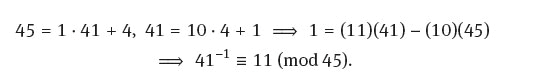
Therefore, using these solutions, the common solution is

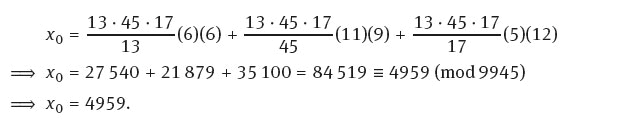
The following theorem describes the structure of modular rings in terms of the multiplicative decomposition of the modulus and is based directly on the Chinese Remainder Theorem.

Theorem 5.7.3. Suppose that m₁, m₂,…, m_k are k positive integers that are relatively prime in pairs and n = m₁m₂ … m_k. Then the map

given by

is a ring isomorphism.

The ā’s in the tuple are the corresponding residue classes for each m_t.

5.8    Exercises

5.1    Verify that the following are rings. Indicate which are commutative and which have identities. Which are integral domains?

(a)  The set of rational numbers.

(b)  The set of continuous functions on a closed interval [a, b] under ordinary addition and multiplication of functions.

(c)  The set of 2 x 2 matrices with integral entries.

(d)  The set n Z consisting of all integers which are multiples of the fixed integer n.

5.2    (a) Show that in an ordered ring, squares must be positive. Conclude that in an ordered ring with identity the multiplicative identity must be positive.

(b)  Show that the complex numbers under the ordinary operations cannot be ordered.

5.3    Show that any ordered ring must be infinite. (Hint: Suppose a > 0 then a + a > 0, a + a + a > 0 and continue.)

5.4    Find the gcd and lcm of the following pairs of integers and then express the gcd as a linear combination

(a)  78 and 30;

(b)  175 and 35;

(c)  380 and 127.

5.5    Prove that if a = qb + r then (a, b) = (b, r).

5.6    Prove that if d = (a, b) then a and b are relatively prime.

5.7    Show that if (a, b) = c then (a², b²) = c². (Hint: The easiest method is to use the fundamental theorem of arithmetic.)

5.8    Show that an integer is divisible by 3 if and only if the sum of its digits (in decimal expansion) is divisible by 3. (Hint: Write out the decimal expansion and take everything modulo 3.)

5.9    Find the multiplicative inverse if it exists

(a)  of 13 in ₄₇;

(b)  of 17 in ₂₂;

(c)  of 6 in ₃₀.

5.10  Solve the linear equations in the given rings

(a)  4x +6 = 2 in ₇;

(b)  5x + 9 = 12 in ₄₇;

(c)  3x + 18 = 27 in ₄₀.

5.11  Find $ (n)for

(a)  n = 17;

(b)  n = 526;

(c)  n = 138.

5.12   Determine the units and write down the group table for the unit group U(_n) for

(a)  12^;

(b)  ₂₆.

5.13  Suppose that G = (g) is also cyclic of order n. Show that the map f : G → (_n, +) given by g → 1 is actually a group isomorphism.

5.14  For any natural number m, let (Z_m, +) denote the additive group of Z_m, and let U(Z_m) be the group of units of Z_m. Let n = n₁ n₂ … n_k be a factorization of n with pairwise relatively prime factors. Then prove that

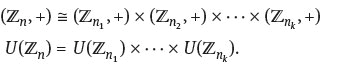
5.15  Prove that if an integer is congruent to 2 modulo 3 then it must have a prime factor congruent to 2 modulo 3.

5.16  Prove that if bc is a perfect square for integers b, c and (b, c) = 1 then both b and c are perfect squares.

5.17  Determine a primitive root modulo 11.

5.18  We outline a proof of the theorem: An integer n will have a primitive root modulo n if and only if

where p is an odd prime.

(a)  Show that if (m, n) = 1 with m > 2, n > 2 then there is no primitive root modulo mn

(b)  Show that there is no primitive root modulo 2^k for k > 2.

(c)  Prove: If p is an odd prime then there exists a primitive root a modulo p such that a^p-1 is not congruent to 1 modulo p². (Hint: Let a be a primitive root modulo p. Then a + p is also a primitive root modulo p. Show that either a or (a + p) satisfy the result.)

(d)  Prove: If p is an odd prime then there exists a primitive root modulo p^k for any k > 2. (Hint: Let a be the primitive root modulo p from part (c). Then this is a primitive root modulo p^k for any k > 2.)

(e)  Prove: If p is an odd prime and if a is a primitive root modulo p^k then, if a is odd, a is also a primitive root modulo 2p^k. If a is even then a + p^k is a primitive root modulo 2p^k.

5.19  If m > 2 show that $ (m) is even.

5.20  Prove that ϕ (n²) = n$ (n) for any positive integer n.

5.21  Prove that if n > 2 then

5.22  Prove that if n has k distinct odd factors then 2^k $ (n).