Therefore n − 1 is a sum of an even number of terms of the same parity so n − 1 must be even. It follows that 2p divides n − 1. Hence b^2p − 1 is a divisor of b^n-1 − 1. However

Therefore n is a pseudoprime to the base b proving the theorem. □

Although there are infinitely many pseudoprimes they are not that common. It has been shown for example that there are only 21 853 pseudoprimes to the base 2 among the first 25 000 000 000 integers. Hence there is a good chance that if a number, especially a large number, passes a test as a pseudoprime, then it is really a prime. The question becomes how to make this chance, or probability, precise. Lists of many pseudoprimes can be found on various internet websites (see [PP]).

From simple congruences it is clear that if n is a pseudoprime to the base b₁ and also a pseudoprime to the base b₂ then it is a pseudoprime to the base b₁b₂.

Probabilistic methods proceed by testing n to a base b₁. If it is not a pseudoprime, then it is composite and we are done. If it is a pseudoprime, test a second base b₂ and so on, in the hope of finding a base where it is not a pseudoprime. However there do exist numbers which are pseudoprimes to every possible base.

Definition 6.6.9. A composite integer n is a Carmichael number if n is a pseudoprime to each base b > 1 with (n, b) = 1.

The Carmichael numbers can be completely classified. Interestingly this was done even before the existence of Carmichael numbers was shown. The following is called the Korselt criterion after A. Korselt.

Theorem 6.6.10. An odd composite number n is a Carmichael number if and only ifn is squarefree and (p − 1) | (n − 1) for every prime p dividing n.

Proof. We first show that if a number n is not squarefree then it cannot be a Carmichael number.

Suppose that n is not squarefree. Then there exists a prime p with p² | n. The multiplicative group in Z_p2 is cyclic, that is there exists a primitive element, (see [FR]), and hence, there is a multiplicative generator g modulo p². Since $ (p²) = p(p − 1) we have g^p(p-1) = 1 (modp²) and this is the least power of g that is congruent to 1 modulo p². Now let m = p₁ •• •p_k where p₁,… ,p_k are the other primes besides p dividing n. Notice that p^k is not a Carmichael number so these primes exist. Choose a solution b to the pair of congruences

b = g (modp²) b = 1 (mod m)

which exists from the Chinese Remainder Theorem. Since b = g (modp²) it follows that b also has multiplicative order p(p − 1) modulo p². Suppose n was a Carmichael number. Then n would be a pseudoprime to the base b and hence

b^n-1 = 1 (mod n).

This implies thatp(p − 1) | n from the multiplicative order of b. However sincep|n we have n −1 = −1 (modp). On the other hand if p(p −1) | n − 1we have n −1 = 0 (modp) a contradiction. Therefore n cannot be a pseudoprime to the base b and hence is not a Carmichael number.

Now suppose that n is squarefree so that n = p₁p₂ •••p_k with k > 2 and the p_i distinct primes. Suppose first that (p₁ − 1) | (n − 1) for i = 1,…, k and suppose that (b, n) = 1. Then

Hence

Therefore n is a pseudoprime to the base b and since b was arbitrary with (b, n) = 1 it follows that n is a Carmichael number.

Conversely, suppose that n = p₁ ••• p_k is a Carmichael number. Let p_{ be one of these primes and suppose that g is a generator of the multiplicative group of Z_p . Recall, as in the proof of the squarefree property, that this group is cyclic. Hence g has multiplicative order p_t −1 modulo p_;. Now let b be a solution to the pair of congruences

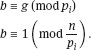
Then b also has multiplicative order p₁ − 1 modulo p_;. Further since (b,p₁) = 1 and to the base b and hence

(b, ⁿ) = 1 it follows that (b, n) = 1. Since n is a Carmichael number it is a pseudoprime

b^n-1 = 1 (mod n) b^n-1 = 1 (modp_;).

It follows that (p₁ − 1) | (n − 1) proving the theorem. □

Corollary 6.6.11. A Carmichael number must be divisible by at least3 primes.

Proof. Suppose that n is a Carmichael number. Then from the proof of the previous theorem n = p₁ -p with k > 2 and thep_t distinct primes. We must show that k > 2. Suppose that n = pq with p < q primes. Since n is a Carmichael number we get from the previous theorem (q − 1) | (n − 1). However

n − 1= pq − 1= p(q − 1 + 1) − 1 = p − 1 (mod(q − 1)).

Since (q − 1) | (n − 1) this would imply that (q − 1) | (p − 1) which is impossible since p < q. Therefore if n = pq it cannot be a Carmichael number and hence k > 2so that n must be divisible by at least 3 distinct primes. □

Using the Korselt criterion we can present an example of a Carmichael number.

Example 6.6.12. The integer n = 561 = 3 ⋅ 11 ⋅ 17 is a Carmichael number. Here n − 1 = 560 which is divisible by 2,10 and 16 and hence by the Korselt criterion it is a Carmichael number. This is well known as the smallest Carmichael number (see exercises).

Carmichael numbers are relatively infrequent. It has been shown for example that there are only 2163 Carmichael numbers among the first 25 000 000 000 integers. However it has been proved by Alford, Granville and Pomerance that there do exist infinitely many Carmichael numbers. There is a list of Carmichael numbers up to 10¹⁶ (see [CP]).

We note that if n > 3 is a Carmichael number, then n must be odd. To see this suppose that n is even. We have (n − 1, n) = 1 and since n is a Carmichael number we have (n − 1)ⁿ⁻¹ = 1 (mod n). On the other side (n − 1)ⁿ⁻¹ = −1 (mod n) since n is even. Hence n | 2so n < 2 which contradicts n > 3. Therefore n must be odd.

For what follows we need the fact that the multiplicative group is cyclic for p > 3 and a > 1 (see [FR]).

Theorem 6.6.13 (The First Probabilistic Primality Test). Let n > 3 be an odd integer which is not a Carmichael number. Choose k > 0 so that (2 )^k is smaller than the desired primality testing error. Consider the following algorithm

(1)  Choose a random number b € {1,…, n − 1}.

(2)  Calculate (b, n). If (b, n) > 1 return composite number and stop.

(3)  Calculate bⁿ⁻¹ modulo n. If bⁿ⁻¹ is not congruent to 1 modulo n return composite number and stop.

(4)  Repeat steps (1), (2), (3) up to k times.

If at each of the k passes bⁿ⁻¹ = 1 (modn) then return n is prime with probability 1-( 1 )^k.

This is a probabilistic algorithm which correctly determines up to a probability > 1 − (1 )^k that n is a prime number.

For the proof of Theorem 6.6.13 we need the following.

Theorem 6.6.14. Let n ≥ 3 be a composite integer.

(a)  Let b €N with (b, n) = 1. Then n is a pseudoprime to the base b if and only if the order ofb in Z* divides n − 1.

(b)  Letb₁, b₂ € Kwith (b₁, n) = (b₂, n) = 1. If n is a pseudoprime to the base b₁ thenn is a pseudoprime to the base b₁b₂ and also to each base b₁a₂ with a^b₂ = 1 in Z*.

(c)  If n is not a pseudoprime to at least one base than n is not a pseudoprime to at least 50 % of the bases b € {1,…,n − 1} with (b, n) = 1.

Proof (of Theorem 6.6.14). (a) Let i = ord(b) = |b| the order of b in Z*. From b = 1 we get that i|(n − 1).

Since the ab_i are pairwise different, there are at least s bases for which n is not a pseudoprime. Further by the pairwise distinctness s is at least 50 % of the bases b € {1,…,n − 1} with(b, n) = 1. □

We can now give the proof of the first probabilistic primality test, Theorem 6.6.13.

Proof (of Theorem 6.6.13). The finiteness of the algorithm is obvious. The correctness of the algorithm is given by part (c) of the above theorem as follows. If n is composite then n is not a pseudoprime to at least one base b € {1,…, n − 1} with (b, n) = 1 because n is not a Carmichael number. Hence by part (c) of Theorem 6.6.6 the integer n is a pseudoprime to at most 50 % of the bases, that is for < 1 of the bases b € {1,…, n − 1}, (b, n) = 1.

Let b₁, b₂ € {1,…, n − 1} with (b₁, n) = (b₂, n) = 1. Then the probability that n is a pseudoprime to the basis b₁ and b₂ is < 11 = 4 because the calculations for b₁ and b₂ are independent.

This proves Theorem 6.6.13. □

6.6.4 Miller-Rabin Primality Testing

Miller and Rabin determined an even stronger test than the primality test given in the previous section.

Definition 6.6.15. Let n be an odd composite integer with n − 1 = 2^st with t odd. If b > 1 and (n, b) = 1 Then n is a strong pseudoprime to the base b if either

(1)  b^l = 1 (mod n) or

(2)  there exists r with 0 < r < s such that b²¹ = −1 (mod n).

The Miller-Rabin Test is based on the following theorem, that was proved independently by Monier and Rabin.

Theorem 6.6.16. For each composite integer n > 9 the number of bases b with 0 < b < n for which n is a strong pseudoprime is less than 4.

The proof of this is long and involved and can be found in [FR].

If n is not a strong pseudoprime to the base b we say that b is a witness for n (a witness that n is composite). Then Theorem 6.6.16 says that at least 4 of all the integers in (1, n − 1) are witnesses for n.

Theorem 6.6.17 (Miller-Rabin PrimalityTest). Letn > 3 be an odd integer. Choose k > 0 so that (2 )^k is smaller than the desired primality testing error. Consider the following algorithm.

(1)  Write n − 1 = 2^st with s > 1 and t odd.

(2)  Consider a random number b € {1,…,n −1} and calculate (b, n). If(b, n) > 1 return composite number and stop.

(3)  Calculate bⁿ⁻¹ modulo n. If bⁿ⁻¹ is not congruent to 1 modulo n return composite number and stop.

(4)  Calculate b^t modulo n. If either b^t = 1 (mod n) orb^t = −1 (mod n) continue with step (6).

(5)  Calculate (b^t)², (b^t)⁴,…, (b^t)^2s modulo n. Ifb^st = −1 (modn) for some i €{1,…,s − 1} continue withstep (6). -}i* ^i-^ ^i−1 *
If at some time b = 1 (mod n) but b is not congruent to 1 modulo n and b is not congruent to −1 modulo n return composite number and stop.

(6)  Repeat steps (2) to (5) up to k times.

If we always have no break off, then give “test passed” and stop.

This is a probabilistic algorithm which correctly determines up to a probability > 1 − (1 )^k that n is a prime number.

Based on the previous theorem, the proof proceeds analogously to the proof in the last section, except that now the probability is > 1 − (1 )^k based on Theorem 6.6.5.

In practice, it is sufficient to test for only a few bases. If n < 2 · 5 · 10¹⁰ there exists only one strong pseudoprime n to the bases 2,3,5, 7.

The Miller-Rabin Test can be made deterministic under the assumption that the Extended Riemann Hypothesis holds (see [FR]). In particular, Bach proved the following.

Theorem 6.6.18. Assuming that the Extended Riemann Hypothesis holds, then for any odd composite integer n there is a witness less than 2(log n)².

Hence based on the theorem, we would only have to test for witnesses less than 2(log n)². If there are none, then n is prime. This is then a deterministic polynomial time algorithm. However it depends on the unproved Extended Riemann Hypothesis.

6.6.5 Mersenne Primes and the Lucas-Lehmer Test

A large portion of primality testing, especially relative to cryptography, has centered on the Mersenne primes. In fact most of the prime records, that is the determination of a largest known prime, involves finding larger and larger Mersenne primes.

A Mersenne number is a positive integer of the form M_n = 2ⁿ −1, with n = 1, 2,…. If M₂ is prime, then M_n is a Mersenne prime. It is not known whether or not there are infinitely many Mersenne primes, however it is conjectured, and believed, that there are infinitely many. For more information on this interesting class of numbers and their properties see [FR].

Testing Mersenne numbers for primality has been particularly fruitful because of the Lucas-Lehmer test. This is a straightforward deterministic primality test specific to the Mersenne numbers. It is relatively easy to implement on a computer and has been quite successful in finding larger and larger Mersenne primes. For the most part historically, the largest known Mersenne prime, is also the largest known prime or current prime record. For a list of prime records see [FR].

Theorem 6.6.19 (Lucas-Lehmer Test). Letp be an odd prime and define the sequence (Bn) inductively by

Then the Mersenne number M_p = 2^p − 1 is a Mersenne prime if and only ifM_p divides

^Sp−1 ^.

A proof of this can be found in [FR]. We note that if M_p is prime we must have p prime.

6.7 Exercises

6.1    Use trial division to determine if any of the following integers are prime.

(a) 10 387

(b) 269

(c) 46 411

6.2    Use the Sieve of Eratosthenes to develop a list of primes less than 300. (Note this list could be used for problem 6.1).

Given positive integers m, x, by a slight modification, the Sieve of Eratosthenes can be used to determine all the positive integers relatively prime to m and less than or equal to x.

Here suppose we are given m andx. Letp₁,…,p_k be the distinct prime factors of m arranged in ascending order, that is p₁ < p₂ < ··· < p_k. Next list all the positive integers less than or equal to x as we did for the ordinary sieve. Start with p₁ and eliminate all multiples of p₁ on the list. Then successively do the same for p₂ through p_k. The numbers remaining on the list are precisely those relatively prime to m that are also less than or equal to x. If p_i > x ignore this prime and all higher primes.

6.3    Use the modified Sieve of Eratosthenes described above to find the integers less than 100 and relatively prime to 891.

Using the Sieve of Eratosthenes, Legendre developed a formula to compute N_m(x), the number of integers less than or equal to x and relatively prime to m. This is called Legendre’s Formula for the Sieve of Eratosthenes. Let m ∈ , x ≥ 0 then

where μ(d) is the Moebius function and [ ] is the greatest integer function.

6.4    Apply Legendre’s formula to evaluate

(a) N₆₅₅(200);

(b) N₈₉₁(100).

6.5    Let P(x) denote the number of primes p ≤ x for which p + 2 is prime. Then by Lemma 6.2.1.4 for x ≥ 3 we have

where c is a constant. Show that this implies that for x ≥ 3

where k is a constant.

6.6    Use the integral test for infinite series to show that

converges.

6.7    Prove that

6.8    Use the Fermat probable prime test to determine if 42671 is prime or not.

6.9    Use the Lucas Test to establish that 271 is prime

6.10  Show that if n is prime and k ≠ 0,1 then the binomial coefficient is congruent to 0 modulo n.

6.11   Use problem 6.10 to show that if p is prime then

6.12   Determine the bases b (if any) 0 < b < 14 for which 14 is a pseudoprime to the base b.

6.13   Prove Lemma 6.3.1.1: If n is a pseudoprime to the base b₁ and also a pseudoprime to the base b₂ then it is a pseudoprime to the base b₁b₂.

6.14  Show that 561 = 3 · 11 · 17 is the smallest Carmichael number. (Use the Korselt criterion together with Corollary 6.3.1.)

6.15  Define the sequence (S_n) inductively by

Let Show that u + v = 4 = S₁ and uv =1. Then use induction to show that

S_n = u²ⁿ⁻¹ + v²ⁿ⁻¹.

6.16   Show that if p, q are primes and e, d are positive integers with (e, (p − 1)(q − 1)) = 1 and ed = 1 (mod(p − 1)(q − 1)) then a^ed = a (modpq) for any integer a. (This is the basis if the decryption function used in the RSA algorithm.

6.17   Show that for the polynomial p(x) = x² − x + 41 the values p(a) for a = 0 ,1,…, 40 are all prime numbers.

Hint: Assume that n² − n + 41 is composite for some n with 0 ≤ n ≤ 40. Let p be the smallest prime factor of this n and show that if n is composite then 163 is a quadratic residue modulo p which gives a contradiction.