9 Basic Concepts from Group Theory
9.1 Groups and Group Theory
Up to this point we have been using algebraic objects arising from number theory, such as the modular rings 
n and elliptic curve groups, to do encryption. These objects are all commutative and hence we can call the type of encryption we have already done as commutative cryptography. In an effort to improve upon cryptographic security, non-commutative cryptography was introduced. Non-commutative cryptography is essentially group based cryptography. In group based cryptography, non-abelian groups and their properties are used in encryption and decryption. There are two primary sources for non-abelian groups: linear groups, that is, groups of matrices, and combinatorial group theory. In this chapter we describe the necessary material from group theory in general, and combinatorial group theory in particular, that is essential for non-commutative cryptographic purposes. First we define a group.
Definition 9.1.1. A group G is a set with one binary operation which we will denote by either multiplication • or just juxtaposition, such that:
(1) The operation is associative, that is, (g1g2)g3 = g1(g2g3) for allg1,g2, g3 e G.
(2) There exists an identity for this operation, that is, an element 1 such that 1g = g and g1 = g for each g e G.
(3) Each g e G has an inverse for this operation, that is, for each g there exists a g−1 with the property that gg−1 = 1 and g−1g = 1.
If in addition the operation is commutative, that is g1g2 = g2g1 for all g1, g2 e G, the group G is called an abelian group.
The order of a group G, denoted |G|, is the number of elements in the group G. If |G| < to, G is a called a finite group, otherwise it is an infinite group.
It follows easily from the definition that the identity is unique and that each element has a unique inverse.
Lemma 9.1.2. If G is a group then there is a unique identity. Further ifg e G its inverse is unique. Finally if g1, g2 e Gthen (g^)−1 = g-^g-1.
Proof. Suppose that 1 and e are both identities for G. Then 1e = e since e is an identity and 1e = 1 since 1 is an identity. Therefore 1 = e and there is only one identity.
Next suppose that g e G and g1 and g2 are inverses for g. Then
g1gg2 = (g1g)g2 = 1g2 = g2
since g1g = 1. On the other hand,
g1gg2 = g1(gg2) = g11 = g1
since gg2 = 1. It follows that g1 = g2 and g has a unique inverse.
Therefore (g21g11) is an inverse forg1g2, and since inverses are unique, it is the inverse of the product. □
Groups most often arise as permutations on a set. We will see this as well as other specific examples of groups in subsequent sections.
Finite groups can be completely described by their group tables or multiplication tables. These are sometimes called Cayley tables. In general, let G = {g1, ...,gn} be a group, then the multiplication table of G is:
The entry in the row of gj e G and column of gj e G is the product (in that order) gg in G.
Groups satisfy the cancellation law for multiplication.
Lemma 9.1.3. If G is a group and a, b, c e G with ab = ac or ba = ca then b = c.
Proof. Suppose that ab = ac. Then a has an inverse a−1 so we have
a−1(ab) = a−1(ac)
From the associativity of the group operation we then have
A consequence of the above lemma is that each row and each column in a group table is just a permutation of the group elements. That is, each group element appears exactly once in each row and each column.
A subset H c G is a subgroup of G if H is also a group under the same operation as G. As for rings and fields a subset of a group is a subgroup if it is non-empty and closed under both the group operation and inverses.
Lemma9.1.4. Asubset H c G is a subgroup if H = 0 and H is closedunder the operation and inverses. That is, if a, b e H then ab e H and a−1, b−1 e H.
Let G be a group and g e G; we denote by gn, n eN, as with numbers, the product of g taken n times. A negative exponent will indicate the inverse of the positive exponent. As usual, let g0 = 1. Clearly group exponentiation will satisfy the standard laws of exponents. Now consider the set
of all powers of g. We will denote this by ⟨g⟩
Lemma 9.1.5. If G is a group and g e G then (g) forms a subgroup of G called the cyclic subgroup generated by g. The subgroup (g) is abelian even ifGis not.
Proof. If g e G then g e (g) and hence (g) is non-empty. Suppose then that a = gm, b = gn are elements of (g). Then ab = gngm = gn+m e (g) so (g) is closed under the group operation. Further a−1 = (gn)−1 = g~n e (g) so (g) is closed under inverses. Therefore (g) is a subgroup.
Finally ab = gngm = gn+m = gm+n = gmgn = ba and hence (g) is abelian. □
Suppose that g e G and gm = 1 for some positive integer m. Then let n be the smallest positive integer such that gn = 1. It follows that the set of elements {1, g, g2,... ,gn-1} are all distinct but for any other power gk we have gk = gt for some k = 0,1,...,n − 1 (see exercises). The cyclic subgroup generated by g then has order n and we say that g has order n which we denote by o(g) = n. If no such n exists we say that g has infinite order.
9.2 Cosets and Normal Subgroups
In applying group theory to cryptography we must understand some things about the structure of groups. In this section we briefly discuss cosets and Lagrange’s theorem, normal subgroups and factor groups and the isomorphism theorems. For more information we refer the reader to [FGR].
We first need the idea of the cosets of subgroup. Let G be a group and let H be a subgroup of G. Then for any a e G, the left coset of a in G with respect to H, denoted by aH, is the set
The right coset of a in G with respect to H, written Ha, is defined similarly as the set
While left cosets do not have to equal right cosets, the number of distinct left cosets of a subgroup H is exactly the same as the number of distinct right cosets. This number is called the index of H in G and is denoted [H : G]. It can be shown that the set of cosets of a subgroup partition the group and further each has the same size as the subgroup H. For finite groups this leads to the following result called Lagrange’s theorem which shows that the order of any subgroup of a finite group must divide the order of the group.
Theorem 9.2.1 (Lagrange’s Theorem). Let G be a finite group and H c G a subgroup. Then |G| = |H|[G : H].
For a finite group this implies that both the order of a subgroup and the index of a subgroup are divisors of the order of the group.
This theorem plays a crucial role in the structure theory of finite groups since it greatly restricts the size of subgroups. For example in a group of order 10 there can be proper non-trivial subgroups only of orders 2 and 5.
As an immediate corollary, we have the following result.
Corollary 9.2.2. The order of any element g e G, where G is a finite group, divides the order of the group. In particular if |G| = nandg e Gfheno(g)|n and gn = 1.
Normal subgroups are special types of subgroups which play a crucial role in determining the structure of a group. Let G be an arbitrary group. A subgroup H is a normal subgroup of G, which we denote by H < G, if g−1Hg = H for all g e G.
Since g−1Hg = H for all g e G it follows that gH = Hg for all g e G and hence for normal subgroups each left coset is also a right coset and vice versa.
Suppose that H1 and H2 are subgroups of a group G. We say that H2 is conjugate to H1 in G if there exists an element a e G such that H2 = aH1a−1. H1, H2 are the called conjugate subgroups of G. For a subgroup H being normal is equivalent to having only one conjugate.
Normal subgroups allow us to build a group structure on the set of cosets. Let G be an arbitrary group and H a normal subgroup of G. Let G/H denote the set of distinct left (and hence also right) cosets of H in G. On this set G/H define the multiplication
for any elements g1 H, g2H in G/H.
We then have the following theorem. For a proof see [FGR].
Theorem 9.2.3. Let Gbe a group and H a normal subgroup of G. Then G/H under the operation defined above forms a group. This group is called the factor group or quotient group ofG modulo H. The identity element is the coset 1H = H and the inverse of a coset gH isg~1H.
Earlier in Chapters 5 and 8 we used the idea of a group homomorphism and group isomorphism. These are closely tied to normal subgroups and factor groups. We now formally discuss them.
If G, H are groups then a homomorphism is a mapping F : G → H such that f(g1g2) = f(g1)f(g2) for all g1,g2 e G. We say that f preserves the group operations. A group homomorphism is an isomorphism if it is also a bijection. Two groups are isomorphic if there exists an isomorphism between them. Isomorphic groups are algebraically the same. If G1 and G2 are isomorphic groups than we write G1 ≅ G2.
Iff : G → H is a group homomorphism. Then the kernel off denoted kerf) is the set of elements of G that map to the identity in H;
We denote the image off, which is a subset of H, as imf). The following result is called the group isomorphism theorem and we sketch a proof in the exercises.
Theorem 9.2.4 (Group Isomorphism Theorem).
(a) Let G1 and G2 be groups andf : G1 → G2 a group homomorphism. Then kerf) is a normal subgroup of G1, imf) is a subgroup ofG2 and
(b) Conversely, suppose that N is a normal subgroup of a group G. Then there exists a group H and a homomorphism f : G → H such that kerf) = N and imf) = H. In particular H = G/N and the map f : G → G/N is called the canonical homomorphism. This isgiven byf(g) = gN.
9.3 Examples of Groups
As already mentioned, groups arise in many diverse areas of mathematics. In this section and the next we present specific examples of groups.
First of all any ring or field under addition forms an abelian group. Hence, for example (Z, +), (Q, +), (R, +), (C, +) where these are respectively the integers, the ra- tionals, the reals and the complex numbers, all are infinite abelian groups. If n is the modular ring. then for any natural number n, n forms a finite abelian group under addition.
In a field F, the non-zero elements are all invertible and form a group under multiplication. This is called the multiplicative group of the field F and is usually denoted by F*. Since multiplication in a field is commutative, the multiplicative group of a field is an abelian group.
The multiplicative group of a field is a special case of the unit group of a ring. If R is a ring with identity, recall that a unit is an element of R with a multiplicative inverse. Hence in the only units are ±1 while in any field every non-zero element is aunit.
Lemma 9.3.1. If R is a ring with identity then the set of units in R forms a group under multiplication called the unit group of R and is denoted by U(R). If R is a field then U(R) = R* the multiplicative group of non-zero elements ofR.
Important for cryptography is the following fact. For a proof we refer to [CFR1].
Theorem 9.3.2. The multiplicative group of a finite field is a cyclic group.
If q is a prime then the modular ring q is a field. Hence we have the corollary.
Corollary 9.3.3. If q is a prime then the multiplicative group Z* is a cyclic group. A generator of this group is called a primitive element modulo q.
This corollary was used in constructing both the Diffie-Hellman and ElGamal protocols.
To present examples of non-abelian groups we turn to matrices. If F is a field we
let
and
Lemma 9.3.4. If F is a field then for n > 2, GL(n, F) forms a non-abelian group under matrix multiplication and SL(n, F) forms a normal subgroup.
GL(n, F) is called the n-dimensional general linear group over F, while SL(n, F) is called the n-dimensional special linear group over F.
Groups play an important role in geometry. In any metric geometry an isometry is a mapping that preserves distance. To understand a geometry one must understand the group of isometries. We look briefly at the Euclidean geometry of the plane E2.
An isometry or congruence motion of E2 is a transformation or bijection T of E2 that preserves distance, that is d(a, b) = d(T(a), T(b)) for all points a, b e E2.
Theorem 9.3.5. The set of congruence motions of E2 formsagroupcalledthe Euclidean group. We denote the Euclidean group by E.
Lemma 9.3.6. If D is a geometric figure in E2 then the set of symmetries of D forms a subgroup of E called the symmetry group ofD denoted by Sym(D).
Example 9.3.7. Let Tbe an equilateral triangle. Then there are exactly six symmetries of T (see exercises). These are:
Sym(T) is called the dihedral group D3. In the next section we will see that it is isomorphic to S3, the symmetric group on 3 symbols.
This can be generalized to any regular n-gon. If D is a regular n-gon, then the symmetry group Dn has 2n elements and is called the dihedral group of order 2n. It is generated by elements r and f which satisfy the relations rn = f2 = 1, f 1rf = rn 1, where r is a rotation of about the center of the n-gon and f is a reflection across a line of symmetry of the regular n-gon.
Hence, D4, the symmetries of a square, has order 8 and D5, the symmetries of a regular pentagon, has order 10.
Groups most often appear as groups of transformations or permutations on a set. In this section we will take a short look at permutation groups.
Definition 9.3.8. If A is a set, a permutation on A is a one-to-one mapping of A onto itself. We denote by SA the set of all permutations on A.
Theorem 9.3.9. ForanysetA, SA forms a group under composition called the symmetric group on A. If | A | > 2 then SA is non-abelian. Further if A, B have the same cardinality, then SA = SB.
If A1 c A then those permutations on A that map A1 to A1 formasubgroupof SA called the stabilizer of A1 denoted stab(Aj).
Lemma 9.3.10. If A1 c A then stab(A^ = {f € SA| f : A1 → A1} forms a subgroup ofSA.
A permutation group is any subgroup of SA for some set A.
We now look at finite permutation groups. Let A be a finite set say A = {a1; a2, ..., an}. Then eachf € SA can be pictured as
For a1 there are n choices for f(a1). For a2 there are only n −1 choices since f is one-to- one. This continues down to only one choice for an. Using the multiplication principle, the number of choices for f and therefore the size of SA is
We have thus proved the following theorem.
Theorem 9.3.11. If |A| = n then |SA| = n!.
For a set with n elements we denote SA by Sn, called the symmetric group on n symbols.
Example 9.3.12. Write down the six elements of S3 and give the multiplication table for the group.
Name the three elements 1,2,3. The six elements of S3 are then:
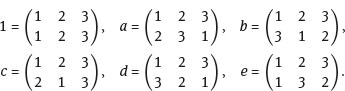
The multiplication table for S3 can be written down directly by doing the required composition. For example,
To see this, note that a : 1 → 2,2 → 3,3 → 1; c : 1 → 2,2 → 1,3 → 3 and so ac : 1 → 3, 2 → 2,3 → 1.
It is somewhat easier to construct the multiplication table if we make some observations. First, a2 = b and a3 = 1. Next, c2 = 1, d = ac, e = a2c and finally ac = ca2.
From these relations the following multiplication table can be constructed
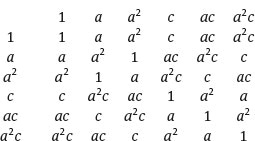
To see this, consider, for example, (ac)a2 = a(ca2) = a(ac) = a2c.
More generally, we can say that S3 has a presentation given by
By this we mean that S3 is generated by a, c, or that S3 has generators a, c and the whole group and its multiplication table can be generated by using the relations
We now consider the case where a group G has a single generator that is a cyclic group.
Definition 9.3.13. A group G is cyclic if there exists a g ∈ G such that G = ⟨g⟩.
In this case G = {gn | n ∈ }, that is G consists of all the powers of the element g. If there exists an integer m such that gm = 1, then there exists a smallest such positive integer say n. It follows that gk = gl if and only if k = l (mod n). In this situation the distinct powers of g are precisely
It follows that |G| = n. We then call G a finite cyclic group. If no such power exists then all the powers of G are distinct and G is an infinite cyclic group.
We show next that any two cyclic groups of the same order are isomorphic.
Theorem 9.3.14.
(a) If G = ⟨g⟩ is an infinite cyclic group then G ≅ (, +) that is the integers under addition.
(b) If G = ⟨g⟩ is a finite cyclic group of order n then G ≅ (n, +) that is the integers modulo n under addition.
It follows that for a given order there is only one cyclic group up to isomorphism.
Theorem 9.3.15. Let G = ⟨g⟩ be a finite cyclic group of order n. Then every subgroup of G is also cyclic. Further ifd | n there exists a unique subgroup of G of order d.
Theorem 9.3.16. Let G = ⟨g⟩ be an infinite cyclic group. Then a subgroup H is of the form H = (gt) for a positive integer t. Further if tl, t2 are positive integers with t1 = t2 then (gt1) and (gt2) are distinct.
Theorem 9.3.17. Let G = ⟨g⟩ be a cyclic group. Then:
(a) IfG = ⟨g⟩ is finite of order n then gk is also a generator if and only if (k, n) = 1. That is the generators of G are precisely those powers gk where k is relatively prime to n.
(b) IfG = ⟨g⟩ is infinite then the only generators are g, g−1.
9.4 Generators and Group Presentations
Crucial to using non-abelian group theory in cryptography is the concept of a group presentation. Roughly for a group G a presentation consists of a set of generators X for G, so that G = (X), and a set of relations between the elements of X from which, in principle, the whole group table can be constructed. In this chapter we make this concept precise. As we will see, every group G has a presentation, but it is mainly in the case where the group is finite, or countably infinite, that presentations are most useful. Historically, the idea of group presentations arose out of the attempt to describe the countably infinite fundamental groups that came out of low dimensional topology. The study of groups using group presentations is called combinatorial group theory.
Before looking at group presentations in general, we revisit two examples of finite groups, and then a class of infinite groups.
Consider the symmetric group on 3 symbols, S3. We saw that it has the following 6 elements:
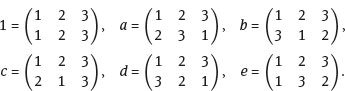
Notice that a3 = 1, c2 = 1 and that ac = ca2. We claim that
is a presentation for S3. First it is easy to show that S3 = ⟨a, c⟩. Indeed
and so clearly a, c generate S3.
Now from (ac)2 = acac = 1 we get that ca = a2c. This implies that if we write any sequence (or word in our later language) in a and c we can also rearrange it so that the only powers of a are a and a2, the only powers of c are c and all a terms precede c terms. For example
Therefore using the three relations form the presentation above each element of S3 can be written as aαcβ with a = 0,1,2 and fi = 0,1. From this the multiplication of any two elements can be determined.
Now let us look at D3, the symmetry group on an equilateral triangle. In the last section we saw that |D31 = 6 and can be generated by a rotation r of 120° around the center of the triangle and a flip f across any of the medians. We then had the relations r3 = f2 = 1, fr = r2f. From these relations the group table can be constructed. Further, the relation fr = r2f can be derived from the relation (rf)2 = 1 combined with r3 = f2 = 1. Hence a presentation for D3 is given by
Notice that except for the change of letters this is the same as the presentation for S3. The map a → r, c → f gives an isomorphism between S3 and D3.
We can also see that D3 is isomorphic to S3 via the following argument. Each symmetry on an equilateral triangle permutes the vertices. Hence each symmetry on an equilateral triangle corresponds to a permutation on 3 symbols. It follows that D3 can be considered as a subgroup of S3. However, |D3| = 6 = |S3| and hence they must be the same.
In general, we let Dn stand for the symmetry group of a regular n-gon. It is called the dihedral group of order 2n. Exactly this same type of argument used for an equilateral triangle applies to all the dihedral groups Dn. Therefore in general |Dn| = 2n and the group is generated generated by a rotation r of angle — about the center of the n-gon and a reflection f about any line of symmetry. The rotation r would have order n so that rn = 1. The reflection f would have order 2 so that f2 = 1. The element rf is then a reflection about the rotated line which is also a line of symmetry. Therefore (rf)2 = 1. Exactly as for D3 the relation (rf)2 = 1 implies that fr = r−1f = rn-1f. This allows us to always place r terms in front of f terms in any word on r and f. Therefore the elements of Dn are always of the form
and further the relations rn = f2 = (rf)2 = 1 allow us to rearrange any word in r and f into this form. It follows that |(r,f}| = 2n and hence Dn = (r,f} together with the relations above. Putting these comments all together we obtain:
Theorem 9.4.1. IfDn is the symmetry group of a regular n-gon then |Dn| = 2n and a presentation for Dn is given by
We now give one class of infinite examples. If G is an infinite cyclic group, so that G ≅ , then G = (g;} is a presentation for G. That is G has a single generator with no relations.
A direct product of n copies of is called a free abelian group of rank n. We will denote this by n. A presentation for n is then given by
9.5 Free Groups and Group Presentations
Crucial to the concept of a group presentation is the idea of a free group.
Definition 9.5.1. A group F is free on a subset X if every map f : X → G with G a group can be extended to a unique homomorphism f : F → G. X is called a free basis for F. In general, a group F is a free group, if it is free on some subset X. If X is a free basis for a free group F we write F = F(X).
We first show that given any set X there does exist a free group with free basis X. Let X = {xi}i∈I be a set (possibly empty). We will construct a group F(X) which is free with free basis X. First let X−1 be a set disjoint from X but bijective to X. If x{ e X then the corresponding element of X−1 under the bijection we denote x−1 and say that x{ and x−1 are associated. The set X−1 is called the set of formal inverses from X and we call X u X−1 the alphabet. Elements of the alphabet are called letters, hence a letter has the form x1 where ∈i = ±1. A word in X is a finite sequence of letters from the alphabet. That is a word has the form
where xt e X and e; = ±1. If n = 0 we call it the empty word which we will denote e. Words of the form x;x−1 or x−1x; are called trivial words. We let W(X) be the set of all words on X.
If w1, w2 e W(X) we say that w1 is equivalent to w2, denoted w1 ~ w2, if w1 can be converted to w2 by a finite string of insertions and deletions of trivial words. For example if w1 = x3x4x−1x2x2 and w2 = x3x2x2 then w1 ~ w2. It is straightforward to verify that this is an equivalence relation on W(X) (see exercises). Let F(X) denote the set of equivalence classes in W(X) under this relation, hence F(X) is a set of equivalence classes of words from X.
A word w e W(X) is said to be freely reduced or reduced if it has no trivial subwords (a subword is a connected sequence within a word). Hence in the example above w2 = x3x2x2 is reduced but w1 = x3x4x−1x2x2 is not reduced. In each equivalence class in F(X) there is a unique element of minimal length. Further this element must be reduced or else it would be equivalent to something of smaller length. Two reduced words in W(X) are either equal or not in the same equivalence class in F(X). Hence F(X) can also be considered as the set of all reduced words from W(X).
Given a word w = x.i1 x.i2 ••• x^” we can find the unique reduced word w equivalent to w via the following free reduction process. Beginning from the left side of w we cancel each occurrence of a trivial subword. After all these possible cancellations we have a word w’. Now we repeat the process again starting from the left side. Since w has finite length eventually the resulting word will either be empty or reduced. The final reduced w is the free reduction of w.
Hence any freely reduced word w has a unique representation
where x^ e X, e; = ±1 and there is no further possible free reduction. The number n of letters in the freely reduced form is called the free length of w denoted by | w|.
Now we build a multiplication on F(X). If
are two words in W(X) then their concatenation w1 * w2 is simply pacing w2 after w1,
If w1, w2 e F(x) then we define their product as
That is we concatenate w1 and w2, and the product is the equivalence class of the resulting word. It is easy to show that if w1 ~ w1 and w2 ~ w2 then w1 * w2 ~ w[ * w2 so that the above multiplication is well-defined. Equivalently we can think of this product in the following way. If w1, w2 are reduced words then to find w1w2 first concatenate and then freely reduce. Notice that if xe.i”x/1 is a trivial word then it is cancelled when the concatenation is formed. We say then that there is cancellation in forming the product w1w2. Otherwise the product is formed without cancellation.
Theorem 9.5.2. LetX be a non-empty set and letF(X) be as above. Then F(X) is a free group with free basis X. Further ifX = 0 then F(X) = {1}, if |X| = 1 then F(X) s and if |X| > 2 then F(X) is non-abelian.
Proof. We first show that F(X) is a group and then show that it satisfies the universal mapping property on X. We consider F(X) as the set of reduced words in W(X) with the multiplication defined above. Clearly the empty word acts as the identity element 1. If w = x/1 x.i2 • • • xe1i” and w. = x.€i”x. “−1 • • • x. i1 then both w * w. and w. * w freely reduce to the empty word and so w1 is the inverse of w. Therefore each element of F(X) has an inverse. Therefore to show that F(X) forms a group we must show that the multiplication is associative. Let
be three freely reduced words in F(X). We must show that
To prove this we use induction on m, the length of w2. If m = 0 then w2 is the empty word and hence the identity and it is certainly true. Now suppose that m = 1 so that w2 = x/1. We must consider exactly four cases.
Case (1): There is no cancellation in forming either w1 w2 or w2 w3. That is xjj1 = x; e’” and xe^ = x,£l1. Then the product w. w2 is just the concatenation of the words and j1 l1 so is (w1w2)w3. The same is true for w1(w2w3). Therefore in this case w1(w2w3) = (w1w2)w3.
Case (2): There is cancellation in forming w1w2 but not in forming w2 w3. Then if we concatenate all three words the only cancellation occurs between w1 and w2 in either w1(w2w3) or in (w1w2)w3 and hence they are equal. Therefore in this case w1(w2w3) = (w1w2)w3.
Case (3): There is cancellation in forming w2w3 but not in forming w1w2. This is entirely analogous to Case (2) so therefore in this case w1(w2w3) = (w1w2)w3.
Case (4): There is cancellation in forming w1w2 and also in forming w2w3. Then xj = x. e’” and xj = x,£l1. Here
On the other hand,
However, these are equal since x^” = x^1. Therefore, in this final case, we have w1(w2w3) = (w1w2)w3. It follows inductively from these four cases that the associative law holds in F(X), and therefore F(X) forms a group.
Now suppose that f : X → G is a map from X into a group G. By the construction of F(X) as a set of reduced words, this can be extended to a unique homomorphism. If w e F with w = x/1 • • • xi” then define f(w) = f(xt)£i1 • • • f(xt. Since multiplication in F(X) is concatenation this defines a homomorphism and again form the construction of F(X) its the only one extending f. This is analogous to constructing a linear transformation from one vector space to another by specifying the images of a basis. Therefore F(X) satisfies the universal mapping property of Definition 9.5.1 and hence F(X) is a free group with free basis X.
The final parts are straightforward. If X is empty the only reduced word is the empty word and hence the group is just the identity. If X has a single letter then F(X) has a single generator and is therefore cyclic. It is easy to see that it must be torsionfree and therefore F(X) is infinite cyclic, that is F(x) s Z. Finally if |X| > 2letx1, x2 e X. Then x1x2 = x2x1 and both are reduced. Therefore F(X) is non-abelian. □
The proof of the above theorem provides another way to look at free groups.
Theorem 9.5.3. F is a free group if and only if there is a generating setX such that every element ofF has a unique representation as a freely reduced word on X.
The structure of a free group is entirely dependent on the cardinality of a free basis. In particular the cardinality of a free basis |X| for a free group F is unique and is called the rank of F. If |X| < to, F is of finite rank. If F has rank n and X = {x1,..., xn} we say that F is free on {x1,..., xn}. We denote this by F(x1, x2,..., xn).
Theorem 9.5.4. IfX and Y are sets with the same cardinality, that is, |X| = |Y|, then F(X) s F(Y), the resulting free groups are isomorphic. Further if F(X) s F(Y) then |X| = |Y |.
Proof. Suppose that f : X → Y is a bijection from X onto Y. Now Y c F(Y) so there is a unique homomorphism $ : F(X) → F(Y) extending f. Since f is a bijection it has an inverse f−1 : Y → X and since F(Y) is free there is a unique homomorphism $1 from F(Y) to F(X) extendingf_1. Then $$1 is the identity map on F(Y) and $1$ is the identity map on F(X). Therefore $, $1 are isomorphisms with $ = $.1.
Conversely suppose that F(X) s F(Y). In F(x) let N(X) be the subgroup generated by all squares in F(X) that is
Then N(X) is a normal subgroup and the factor group F(X)/N(X) is abelian where every non-trivial element has order 2 (see exercises). Hence F(X)/N(X) can be considered as a vector space over 2, the finite field of order 2, with X as a vector space basis. Hence |X| is the dimension of this vector space. Let N(Y) be the corresponding subgroup of F(Y). Since F(X) s F(Y)wewouldhaveF(X)/N(X) s F(Y)/N(Y) and therefore |Y| is the dimension of the vector space F(Y)/N(Y). Therefore |X| = | Y| from the uniqueness of dimension of vector spaces. □
Expressing an element of F(X) as a reduced word gives a normal form for elements in a free group F. This solves what is termed the word problem for free groups. Another important concept is the following: a freely reduced word W = x^x^ •••xl” is cyclically reduced if v1 = vn or if v1 = vn then e1 = -en. Clearly then every element of a free group is conjugate to an element given by a cyclically reduced word. This provides a method to determine conjugacy in free groups.
Theorem 9.5.5. In a free group F two elements g1, g2 are conjugate if and only if a cyclically reduced word for g1 is a cyclic permutation of a cyclically reduced word for g2.
The theory of free groups has a large and extensive literature. We close this section by stating several important properties. Proofs for these results can be found in [MKS], [LS], or [CRR].
Theorem 9.5.6. A free group is torsion-free.
From Theorem 9.4.2 we can deduce:
Theorem 9.5.7. An abelian subgroup of a free group must be cyclic.
Finally a celebrated theorem of Nielsen and Schreier states that a subgroup of a free group must be free.
Theorem 9.5.8. (Nielsen-Schreier). A subgroup of a free group is itself a free group.
Combinatorially 1F is free on X if X is a set of generators for F and there are no nontrivial relations. In particular:
There are several different proofs of this result (see [MKS], [LS], or [CRR]) with the most straightforward being topological in nature. Later we will give an outline of a simple topological proof.
Nielsen, using a technique now called Nielsen transformations in his honor, first proved this theorem about 1920 for finitely generated subgroups. Schreier shortly after found a combinatorial method to extend this to arbitrary subgroups. Complete versions of the original combinatorial proof appear in [MKS], [LS], [CRR], and in the notes by Johnson [Joh].
Schreier’s combinatorial proof also allows for a description of the free basis for the subgroup. In particular, let F be free on X, and H c F a subgroup. Let T = {ta} be a complete set of right coset representatives for F modulo H with the property that if ta = x^ x^ ■■■x^ € T, with et = ±1, then all the initial segments 1,,x^xv, etc. are also in T. Such a system of coset representatives can always be found and is called a Schreier system or Schreier transversal for H. If g € F let g represent its coset representative in T and further define for g € F and t € T, Stg = tg(tg)−1. Notice that Stg € H for all t, g. We then have:
Theorem 9.5.9. (Explicit Form of Nielsen-Schreier). LetF be free on X and Ha subgroup ofF. If T is a Schreier transversal for F modulo H then H is free on the set {Stx| t € T, x € X, Stx =1}.
Example 9.5.10. Let F be free on {a, b} and H = F(X2) the normal subgroup of F generated by all squares in F .
Then F/F(X2) = {a,b;a2 = b2 = (ab)2 = 1) = 2 xZ2.It followsthat aSchreier system for F modulo H is {1, a, b, ab} with a = a, b = b and ba = ab. From this it can be shown that H is free on the generating set
x1 = a , x2 = bab a , x3 = b , x4 = abab , x5 = ab a .
The theorem also allows for a computation of the rank of H given the rank of F and the index. Specifically:
Corollary 9.5.11. Suppose F is free of rank n and |F : H| = k. Then H is free of rank nk - k + 1.
From the example we see that F is free of rank 2, H has index 4 so H is free of rank 2 ■ 4 - 4+ 1 = 5.
9.6 Group Presentations
The significance of free groups stems from the following result which is easily deduced from the definition, and will lead us directly to a formal definition of a group presentation. Let G be any group and F the free group on the elements of G considered as a set. The identity map f : G → G can be extended to a homomorphism of F onto G, therefore:
Theorem 9.6.1. Every group G is a homomorphic image of a free group. That is let G be any group. Then G = F/N where F is a free group.
In the above theorem, instead of taking all the elements of G we can consider just a set X of generators for G. Then G is a factor group of F(X), G s F(X)/N. The normal subgroup N is the kernel of the homomorphism from F(X)onto G. We use Theorem 9.4.1 to formally define a group presentation.
If H is a subgroup of a group G then the normal closure of H denoted by N(H) is the smallest normal subgroup of G containing H. This can be described alternatively in the following manner. The normal closure of H is the subgroup of G generated by all conjugates of elements of H.
Now suppose that G is a group with X a set of generators for G. We also call X a generating system for G. Now let G = F(X)/N as in Theorem 9.3.1 and the comments after it. N is the kernel of the homomorphism f : F(X) → G. It follows that if r is a free group word with r e N then r = 1 in G (under the homomorphism). We then call r a relator in G and the equation r = 1 a relation in G. Suppose that R is a subset of N such that N = N(R), then R is called a set of defining relators for G. The equations r = 1, r e R, are a set of defining relations for G. It follows that any relator in G is a product of conjugates of elements of R. Equivalently r e F(X) is a relator in G if and only if r can be reduced to the empty word by insertions and delations of elements of R and trivial words.
Definition 9.6.2. Let G bea group. Then a group presentation for G consists of a set of generators X for G and a set R of defining relators. In this case we write G = <X; R>. We often write the presentation in terms of defining relations as G = <X; r =1, r e R>.
From Theorem 9.3.1 it follows immediately that every group has a presentation. However, in general there are many presentations for the same group. If R c R1 then R1 is also a set of defining relators.
Lemma 9.6.3. Let Gbea group. Then G has a presentation.
If G = <X; R> and X is finite then G is said to be finitely generated. If R is finite, G is finitely related. Ifboth X and R are finite, G is finitely presented.
Using group presentations we get another characterization of free groups.
Theorem 9.6.4. F is a free group if and only if F has a presentation of the form F = <X;>.
Mimicking the construction of a free group from a set X, we can show that to each presentation corresponds a group. Suppose that we are given a supposed presentation <X; R> where R is given as a set of words in X. Consider the free group F(X) on X. Define two words w1, w2 on X to be equivalent if w1 can be transformed into w2 using insertions and deletions of elements of R and trivial words. As in the free group case this is an equivalence relation. Let G be the set of equivalence classes. If we define multiplication, as before, as concatenation followed by the appropriate equivalence class, then G is a group. Further, each r e R must equal the identity in G, so that G = <X; R>. Notice that here there may be no unique reduced word for an element of G.
Theorem 9.6.5. Given <X; R> where X is a set and R is a set of words on X. Then there exists a group G with presentation <X; R>.
We now give some examples of group presentations.
Example 9.6.6. A free group of rank n has a presentation
Example 9.6.7. A free abelian group of rank n has a presentation
Example 9.6.8. A cyclic group of order n has a presentation
Example 9.6.9. The dihedral groups of order 2n representing the symmetry group of a regular n-gon has a presentation
We looked at this example in Section 9.3.
9.6.1 The Modular Group
In this section we give a more complicated example that will be used in group based cryptography.
If R is any ring with an identity then the set of invertible n x n matrices with entries from R forms a group under matrix multiplication called the n-dimensional general linear group over R (see [Rot]). This group is denoted by GLn(R). Since det(A) det(B) = det(AB) for square matrices A, B, it follows that the subset of GLn(R) consisting of those matrices of determinant 1 forms a subgroup. This subgroup is called the special linear group over R and is denoted by SLn(R). In this section we concentrate on SL2(), or more specifically a quotient of it, PSL2() and find presentations for this group.
The group SL2() consists of 2 x 2 integral matrices of determinant one:
SL2() is called the homogeneous modular group and an element of SL2() is called a unimodular matrix.
If G is any group, recall that its center, Z(G) consists of those elements of G which commute with all elements of G, that is,
Z(G) is a normal subgroup of G, and hence we can form the factor group G/Z(G). For G = SL2(), the only unimodular matrices that commute with all others are ±I = ± (10). Therefore
The quotient
is denoted PSL2() and is called the projective special linear group or inhomoge- neous modular group. More commonly PSL2() is just called the Modular Group
and denoted by M .
M arises in many different areas of mathematics including number theory, complex analysis, Riemann surface theory and the theory of automorphic forms and functions. M is perhaps the most widely studied single finitely presented group. Complete discussions of M and its structure can be found in the books [Fin], [New], and [CRR].
Since M = PSL2() = SL2()/{I,-I} it follows that each element of M can be considered as ±A where A is a unimodular matrix. A projective unimodular matrix is then
The elements of M can also be considered as linear fractional transformations over the complex numbers
Thought of in this way, M forms a Fuchsian group, which is a discrete group of isome- tries of the non-Euclidean hyperbolic plane. The book by Katok [Kat] gives a solid and clear introduction to such groups. This material can also be found in condensed form in [FR].
We now determine presentations for both SL2() andM = PSL2().
Theorem 9.6.10. The group SL2() is generated by the elements
Further, a complete set of defining relations for the group in terms of these generators is given by
It follows that SL2() has the presentation
Proof. We first show that SL2() is generated by X and Y, that is, every matrix A in the group can be written as a product of powers of X and Y.
Let
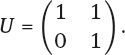
Then a direct multiplication shows that U = XY, and we show that SL2() is generated by X and U which implies that it is also generated by X and Y. Further,
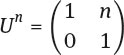
so that U has infinite order.
Let A=(a, b) e .The we have
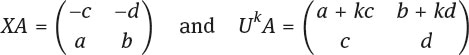
for any k ∈ . We may assume that |c| <|a|. Otherwise start with XA rather than A. If c =0 then A = ±Uq for some q.If A = Uq then certainly A is in the group generated by X and U .If A = -Uq then A = X2 Uq since X2 = -I. It follows that here also A is in the group generated by X and U.
Now suppose c = 0. Apply the Euclidean algorithm to a and c in the following modified way:
where rn = ±1 since (a, c) = 1. Then
Therefore
with m = 0,1,2,3; q0, q1,...,qn+1 e Zand q0,...,qn = 0. Therefore X and U and hence X and Y generate SL2().
We must now show that
are a complete set of defining relations for SL2(), or equivalently, that every relation on these generators is derivable from these. It is straightforward to see that X and Y do satisfy these relations. Assume then that we have a relation
with all ei, aj e Z. Using the set of relations
