1.1 Nonlinear System Modeling: Background, Motivation and Opportunities

1.2 Key Factors in Defining Adaptive Learning Methods for Nonlinear System Modeling

Nonlinear system modeling is a very wide field of research. This book mainly focuses on those methodologies for nonlinear modeling that involve any adaptive learning approach to process data coming from an unknown nonlinear system. Such adaptive learning methods aim at estimating the nonlinearity introduced by the unknown system on the available data. This allows one to identify and model the unknown nonlinear system.

A typical scheme of the adaptive modeling of an unknown nonlinear system is shown in Fig. 1.1, where the system to be modeled receives an input $x\left(n\right)$ and generates a nonlinear output $d\left(n\right)$, possibly including any additive noise. A nonlinear model, receiving the same input $x\left(n\right)$ of the unknown system, is employed to “learn” the behavior of a system from its response and try to perform exactly like it. In order to estimate at best the behavior of the unknown system, a suitable choice of the model must be made. Moreover, the parameters of the chosen nonlinear model need to be optimized by an adaptive procedure, usually based on a cost function involving the response $d\left(n\right)$ of the unknown system and the nonlinear output $y\left(n\right)$ produced by the nonlinear model.

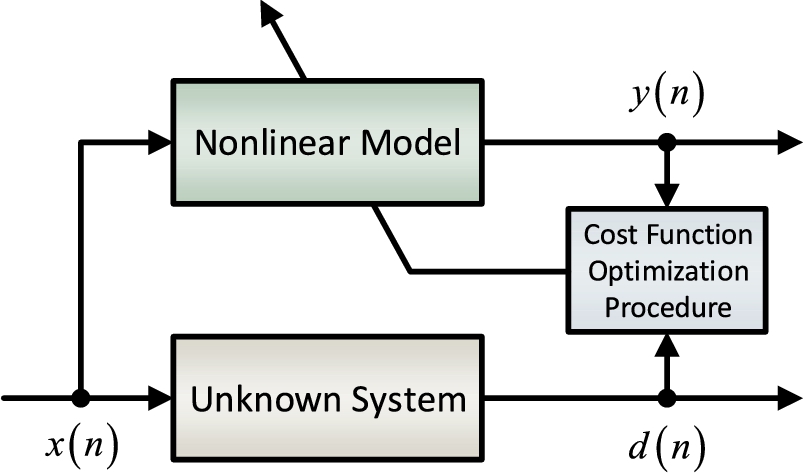
Adapting a model can depend on many factors, which can strongly affect its strategy. The knowledge of such information allows one to treat an unknown system as a gray box and therefore to provide a reliable modeling. Here we want to focus on key aspects that can affect the design of the learning strategy.

One of the first aspects that are evaluated in a model design is the formulation of the problem to be addressed, according to which adaptation models can be different. For example, different choices can be made for a problem of classification rather than a regression one, for identification rather than prediction, etc.

However, one of the most significant factors that determine the learning of a model are input data. Most of the modern theory in machine learning and signal processing is based on the learning from data paradigm (see [15,16], among others). According to data received by a model, a learning strategy is able to identify the desired solution within a set of hypotheses by minimizing a chosen cost function. Input data can be received from a single source or from multiple sources, even asynchronously and heterogeneously, as is often the case in the era of big data. In this sense, the amount of data to process is definitely crucial information for model design.

In addition to the amount of data, it is important to know the rate with which these data arrive at the model. Based on this information, input data can be analyzed altogether (offline learning) or progressively (online learning) (see for example [17,18]). This book will focus in particular on online learning methods for nonlinear modeling. Online learning can be performed in the following ways:

A special case of online learning is real-time learning, which occurs when the iteration index coincides with the time index.

Another aspect that cannot be neglected concerns the architecture of the proposed method. Depending on the problem, the nonlinear modeling method can be implemented by a simple filter, or by a neural network, rather than by more complex structures of distributed and cooperating agents on networks or even on graphs. In this book, the recent proposals in this respect will be presented.

Finally, modeling a nonlinearity with an online approach allows us to consider a wide range of application situations in which nonlinearity can vary during iterations, showing nonstationary and dynamic behaviors. This is definitely one of the key aspects for choosing an online approach to modeling nonlinear systems. Furthermore, due to the recent technology progress and, in particular, to the always growing availability of computational resources and calculation tools, online learning strategies have given the possibility to develop effective nonlinear methods that are also computationally efficient and even suited for real-time data analysis and processing. This is the reason why this book aims to provide a view on the recent methodologies that show an adaptive learning theory aimed at the identification and modeling of several and complex nonlinear systems.

1.3 Book Organization

This book contains 15 chapters, including this one. We aim at covering the most significant topics of the recent years among the field of nonlinear system modeling in the next 14 chapters, divided in four parts.

Part 1  Part 1 is composed of three chapters (2–4) and it deals with linear-in-the-parameter (LIP) nonlinear filters. This class of nonlinear filters won popularity in the past with adaptive Volterra filters, but it is again receiving increasing interest in recent years due to the possibility of combining the strength of complex nonlinear models with the flexibility of linear adaptive filters.

Chapter 2, by Alberto Carini et al., provides an exhaustive overview on LIP nonlinear filters, including the theoretical aspects that contributed to making these methods effective and reliable. This class of filters includes several kinds of models and it is presented under a unified framework. In particular, the chapter introduces the orthogonal LIP nonlinear filters, which leverage the orthogonality of basis functions to improve the robustness of the model. In order to guarantee the orthogonality of the basis functions, the development and use of perfect periodic sequences, together with the multiple-variance identification method, is also introduced. Finally, the chapter proves by experimental results that this kind of filters is capable of providing fast convergence of gradient descent adaptation algorithms and efficient identification of the nonlinear systems.

Chapter 3, by Michele Scarpiniti et al., presents an overview of a family of LIP nonlinear filters, known as Spline Adaptive Filters (SAFs), consisting of a cascade of a linear adaptive filter and a flexible memoryless nonlinear spline function. The peculiarity of SAFs is that the shape of the spline function can be modified during learning, by including the spline control points in the overall adaptive optimization procedure. SAF mainly uses B-splines and Catmull–Rom splines, since they allow one to impose simple constraints on control parameters. Due to the flexibility and ease of implementation, SAFs can be applied to several real-world nonlinear problems and some examples can be found in this chapter.

Chapter 4, by Christian Hofmann et al., introduces and reviews the Significance-Aware (SA) filtering concept, which aims at decomposing the model for an unknown system and its adaptation mechanism into synergetic subsystems to achieve high computational efficiency. The decomposition can be performed according to serial or parallel strategies. The SA approach perfectly fits with LIP nonlinear filters, as proved in this chapter. Among LIP filters, cascade models, cascade group models and bilinear cascade models have been taken into account using both time-domain and frequency-domain adaptive algorithms. The derived models have been applied to the challenging problem of nonlinear acoustic echo cancellation.

Part 2  Part 2 is composed of four chapters (5–8) and it presents some of the most significant recent advances on nonlinear modeling by using adaptive methods based on kernel functions. This family of methods is closely related to the concept of LIP nonlinear filters, since it involves online kernel learning methods, which are implemented as linear learning methods with input data being transformed into a high-dimensional feature space. The difference with respect to the methods presented in Part 1 mainly lies in the feature space, which is induced by applying Mercer's theorem [19]. This property entails a strong and consolidated theory with several desirable features for nonlinear modeling, which have given rise, in the recent years, to an extensive literature on these models. This is the reason why we devote an entire part of the book to these methods.

One of most popular kernel-based methods is represented by the kernel adaptive filter (KAF). Most of the existing KAFs are obtained by minimizing the well-known mean square error (MSE), which is computationally simple and very easy to implement. However, the MSE may show a lack of robustness in the presence of non-Gaussian noises. Chapter 5, by Badong Chen et al., addresses this problem by leveraging the correntropy, which is a similarity measure involving all even-order moments, thus being robust to the presence of heavy-tailed non-Gaussian noises. The chapter shows that KAFs based on the maximum correntropy criterion (MCC) provide an effective solution for the modeling of those nonlinearities that bare nonstationarity and non-Gaussianity properties.

Kernel-based methods are also widely used in machine learning applications. One example is described in Chapter 6, by Yinan Yu et al., where kernel approximation is represented as a subspace learning technique for feature construction for pattern recognition. Kernel approximation aims at reducing the computational complexity, which belongs to the most challenging issue for kernels, since complexity does not scale well with respect to the training size. Considering the kernel approximation as an approximated subspace in a high-dimensional space, it is possible to extract feature vectors onto the approximated subspace, thus subsequently applying a linear learning technique. The chapter also introduces possible learning criteria for adaptive kernel approximation and suitable infrastructures for an efficient implementation.

The problem of the growing size of the kernels is addressed for a different field of applications in Chapter 7, by Pantelis Bouboulis et al. In particular, the chapter introduces an approach based on random Fourier features to approximate kernels without compromising performance. The approximation procedure of random Fourier features is applied to several online kernel-based schemes. More importantly, this rationale has also been applied to learning over distributed networks, in which several nodes collect the observations in a sequential fashion and each node communicates with a subset of nodes to reach a consensus for the overall solution.

The problem of inferring a function defined over the nodes of a network is also addressed in Chapter 8, by Vassilis N. Ioannidis et al. Nodal attributes can be represented as signals that take values over the vertices of the underlying graph, thus allowing the associated inference tasks to leverage node dependencies captured by a graph structure. This chapter presents a unifying framework for tackling signal reconstruction problems over graphs by using kernel-based learning both in the traditional time-invariant, as well as in the more challenging time-varying setting. Furthermore, a flexible model is also introduced based on online multikernel learning (MKL) that selects an optimal combination of kernels “on-the-fly”.

Part 3  Part 3 contains three chapters (9–11) and deals with algorithms and architectures for the modeling of complex nonlinear systems. Very often in real-world problems, one model is not sufficient to estimate an unknown nonlinear environment, due to the complexity of the nonlinearity or often to its variability during the modeling process, which may require a change of the parameter setting of the chosen model or even the change of the adopted nonlinear model. This leads to the use of complex architectures composed of different learning machines, which can even partially contribute to the overall nonlinear modeling. Complex architectures provide performance improvement, but also some issues like overfitting, gradient noise introduction and weak stability, among others. In this part, some recent advances on nonlinear modeling with multiple learning machines are presented, with the goal of achieving accurate nonlinear modeling while avoiding unwanted issues.

Chapter 9, by Nuri Denizcan Vanli et al., introduces a solution for overcoming issues like overfitting, stability and convergence, which can affect nonlinear methods. To this end, self-organizing trees (SOTs) are proposed to be used for regression and classification algorithms. SOTs adaptively partition the feature space into small regions and combine simple local learners defined in such regions. The cumulative loss is minimized by learning both the partitioning of the feature space and the local learners. The overall output of this architecture is achieved by a particular combination of the partition outputs. The proposed method can be applied to different constructions of the tree in order to solve a wide range of complex nonlinear problems, e.g., characterized by nonstationary environments, big data inputs, chaotic signals and very complex nonlinear functions.

A particular cause of complexity in nonlinear modeling may be represented by problems in distributed environments, e.g., wireless sensor networks and peer-to-peer networks. In such problems, a number of agents are required to estimate a common nonlinear model, based on received input data, by combining local computations and information coming from neighboring agents. Chapter 10, by Simone Scardapane et al., addresses this kind of problems, which can be distinguished in single-task problems, characterized by a common model for all the agents, and multitask problems, where each agent might converge to a slightly different model due to some specific factors. Several nonlinear adaptive methods can be used for this kind of architectures, and in this chapter an example is presented involving a kernel-based algorithm for the multitask case.

Nonlinear methods are often difficult to be tuned over an unknown nonlinearity. Moreover, complex nonlinearities, e.g., varying in time, can create even more uncertainty in the nonlinear model to be adopted. In order to tackle this problem, Chapter 11, by Luis A. Azpicueta-Ruiz et al., introduces combined filtering architectures for nonlinear modeling. One of the most useful approaches involves the combination of filters from the same family but having different parameter setting, which aims at simplifying the parameter selection and/or at improving the overall performance. A second combination approach is also presented in which, given a nonlinear architecture with different constituents (e.g., filters, filter partitions or general learning machines), only relevant nonlinear elements are adaptively chosen by optimizing the modeling performance. Several nonlinear methods can be adopted to be used in the presented combined schemes and some examples are shown in this chapter.

Part 4  Part 4 presents four chapters (12–15) dealing with nonlinear modeling by neural processing systems. Neural methods are powerful tools to model several kinds of nonlinearities that can hardly be modeled by other nonlinear methods. One example is represented by dynamical nonlinearities, which often occur in real-world applications. In this book, we show that neural-based models can be applied and used in different systems and for very different applications. In particular, neural systems are here used for nonlinear modeling problems for multidimensional data processing, for the behavioral analysis of spiking activities and, in the last two chapters, for adaptive control systems.

Chapter 12, by Yili Xia et al., deals with the processing of real-world multidimensional data, typically 3D or 4D, such as measurements from body sensor networks or from ultrasonic anemometers, which often entail nonlinear and nonstationary behavior. Since the quaternion domain offers a convenient means to process this kind of data, this chapter proposes quaternion-valued learning methods for the nonlinear modeling of multidimensional data. In particular, quaternion-valued echo state networks (QESNs) are introduced based on quaternion nonlinear activation functions with local analytic properties. QESNs provide efficient computational load for training and favorable analytical conditions in developing full quaternion-valued nonlinearities. Moreover, the proposed method is proved to be second-order optimal for the generality of quaternion signals. The method is evaluated with both simulated and real-world scenarios, including 3D body motion tracking and wind forecasting.

Chapter 13, by Dong Song et al., addresses the problem of identifying short-term and long-term synaptic plasticity from spiking activities. In particular, the chapter proposes a nonstationary dynamical modeling approach in which the synaptic strength is represented as input–output dynamics between neurons, the short-term synaptic plasticity is defined as input–output nonlinear dynamics, the long-term synaptic plasticity is formulated as the nonstationarity of such nonlinear dynamics, and the synaptic learning rule is the function governing the characteristics of the long-term synaptic plasticity based on the input–output spiking patterns.

In Chapter 14, by Hamidreza Modares et al., neural networks are used for the implementation of reinforcement learning algorithms for the adaptive $H_{\inf }$ control of nonlinear systems. In particular, this chapter introduces an adaptive optimal controller for nonlinear continuous-time systems without any knowledge about the system dynamics or the command generator dynamics. First, an augmented system is constructed from the tracking error dynamics and the command generator dynamics to introduce a new performance function. Then a reinforcement learning approach is used to solve the optimal tracking control problem. The proposed method offers several possibilities to be employed in real-world applications, including mobile robots, unmanned aerial vehicles and power systems.

The optimal adaptive control problem is also addressed in Chapter 15, by Biao Luo et al., but with reference to distributed parameter systems (DPSs). The resulting problem is described by highly dissipative nonlinear partial differential equations. The proposed method exploits empirical eigenfunctions of the DPS and the singular perturbation technique to obtain a finite-dimensional slow subsystem of ordinary differential equations that accurately describes the dominant dynamics of the DPS. Then the optimal control problem is reformulated on the basis of the slow subsystem that leads to solve a Hamilton–Jacobi–Bellman equation by using adaptive dynamic programming methods based on neural networks. An adaptive optimal control method based on policy iteration is developed for partially unknown DPSs.

1.4 Further Readings

Topics included in this book, described in the previous section, aim to provide an overview on the recent advances about adaptive learning methods for nonlinear system modeling. However, several noteworthy works on this topic have been populating the literature of the very last years. Among these works, we want to mention some related to the following aspects of nonlinear modeling: LIP nonlinear filters [20–24], time series modeling [25–28], Bayesian learning methods [29,30], kernel-based methods [31–36], nonlinear filtering architectures [37–41], nonlinear dynamic systems [42–44] and nonlinear system control [45–49].