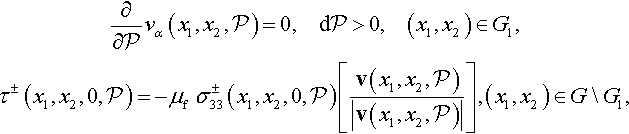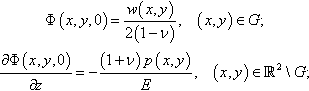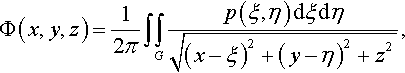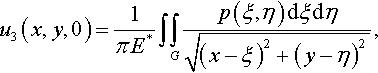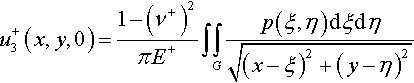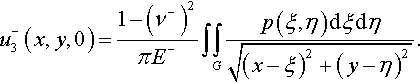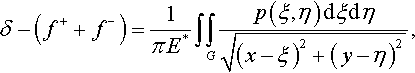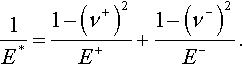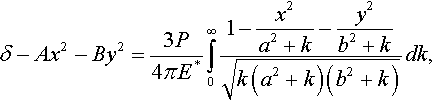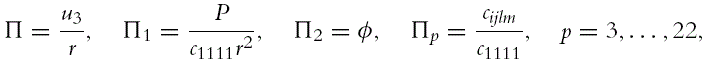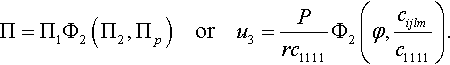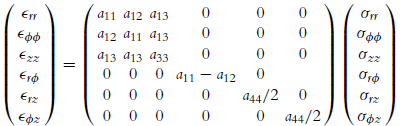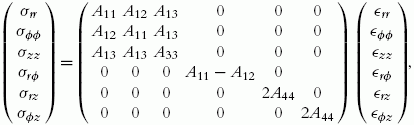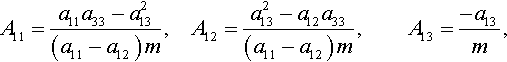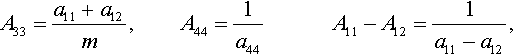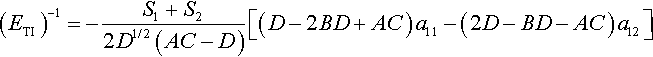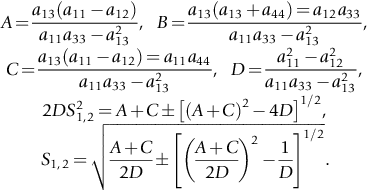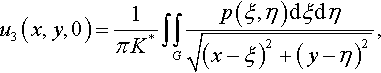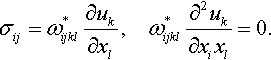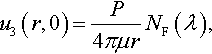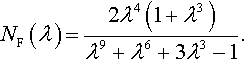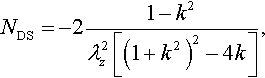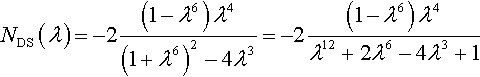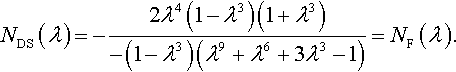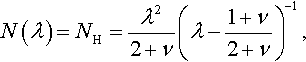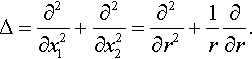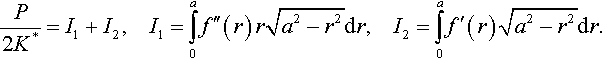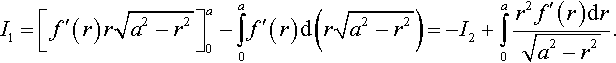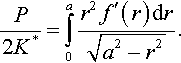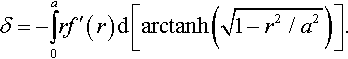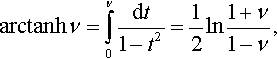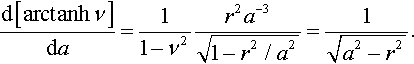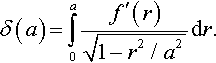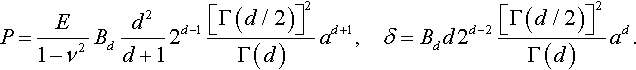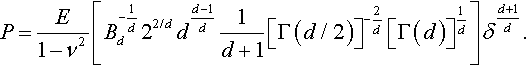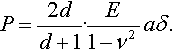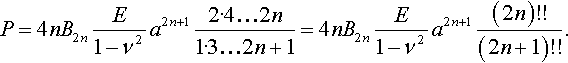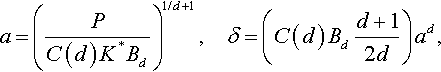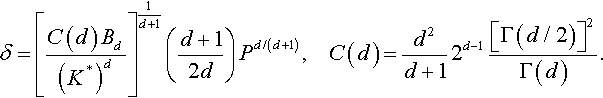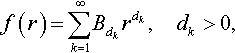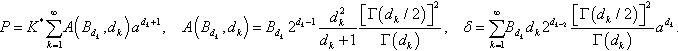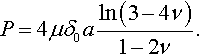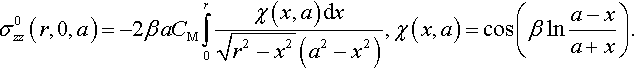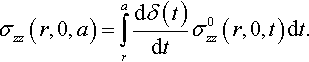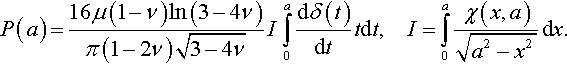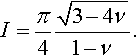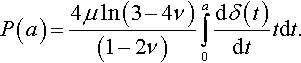The Hertz-Type and Adhesive Contact Problems for Depth-Sensing Indentation
Feodor M. Borodich School of Engineering, Cardiff University, Cardiff CF24 0AA, United Kingdom
Abstract
Connections between the Hertz-type contact problems and depth-sensing indentation of materials are studied. Formulations of Hertz-type contact problems with various boundary conditions within the contact area are discussed in detail. The problems under investigations can be subdivided into two large groups: self-similar problems for anisotropic materials with various rheological properties and adhesive contact problems for arbitrary bodies of revolution or for power-law shaped blunt indenters. Specific features of indentation problems are described and the common methods for extracting elastic and adhesive properties of materials are briefly reviewed. The basic formulae are extended to the case of nonslipping boundary conditions between a probe and the material. The main formulae of the JKR theory of adhesion are extended to any material with rotational symmetry of the elastic properties. These materials include not only isotropic or transversely isotropic elastic solids but also homogeneously prestressed isotropic or transversely isotropic nonlinear elastic materials. The BG method introduced for extracting adhesive and elastic properties of isotropic elastic materials from depth-sensing diagrams of spherical indenters, is described and extended to linear or linearized materials with rotational symmetry of the elastic properties.
1 Introduction
The production of modern optical, microelectromechanical, and biomedical systems and the development of many modern technologies such as the deposition of very thin coating films require the evaluation of mechanical properties of materials of very small volumes. The traditional methods for testing materials are not applicable for this purpose, and therefore other techniques for testing materials have to be developed. Currently depth-sensing indentation (DSI) techniques are widely used for estimations of properties of small or very thin material samples. DSI means that the P–δ curve is continuously monitored (Kalei, 1968), where P is the load applied to a probe and δ is the displacement (the approach of the distant points of the probe and the sample). If the maximum depth of indentation is below the micrometer scale, then the DSI techniques are referred to as depth-sensing nanoindentation. It is often argued that nanoindentation P–δ curves provide a fingerprint of a material’s response to contact loading. The theoretical basis for analysis of experimental P–δ curves and the interpretation of the indentation results are usually based on the use of the Hertz-type contact problems. Hence, problems of interaction between a probe (an indenter or a punch) and a material sample are of interest for both materials science and solid mechanics. Our purpose here is to present a critical review of connections between analytical studies of contact problems and extraction of mechanical properties of materials by the DSI techniques. In addition, we present some new generalizations of known theories and approaches.
In contact mechanics it is assumed that material properties are known, and one needs to find the displacement and stress fields in contacting solids. However, in application to testing of materials, the treatment of contact problems is often confined to the determination of the parameters δ and the contact region, while the determination of the full fields of displacements and stresses is not considered. Thus, studying contact problems, we concentrate more in this article on an analysis of the relations between P, δ, and the size of the contact region l rather than on results for stress fields for particular problems, although the stress fields will be discussed in some cases to clarify specific properties of the problems. Note that for a rigid indenter, the depth of indentation is traditionally denoted by h in the materials science community, while in contact mechanics this parameter is usually denoted as above, i.e., by δ.
From a mathematical point of view, the contact mechanics and materials science approaches are not the same. The contact problems use direct approaches because material properties of contacting solids are given. On the other hand, the problems in materials science are the inverse: one needs to estimate material properties of the sample using the experimental relations between P, δ, and the imprint size, and employing the appropriate relations derived from the solutions of the direct Hertz-type contact problems (Boussinesq, 1885; Hertz, 1882a) with some simplifying assumptions. In the overwhelming majority of research papers, the theoretical analysis of contact is often limited to studying problems for axisymmetric indenters (bodies of revolution) and isotropic, linear elastic materials. Hence, axisymmetric contact problems will be the core of this article. In particular, we will extend the approach of Galin (1946, 1961) to frictionless contact of axisymmetric solids to the case of many linear or linearized materials having rotational isotropy of their mechanical properties and will study the properties of these solutions.
Chaudhri and Lim (2007) argued that the current methods of nanoindentation data analysis may lead to incorrect and misleading results. I believe that the source of many of these disagreements is the violation of the conditions of the Hertz approach. Hence, the formulations of the Hertz-type contact problems, incompatibility of these formulations, and some possible refined problem formulations (see, e.g., Galanov, 1983) are discussed in detail. The known solutions to the Hertz-type contact problems in both frictionless and nonslipping boundary conditions are studied. Two theorems on the slopes of the P–δ curves of axisymmetric contact problems for these types of boundary conditions are formulated and proved.
Further, some specific features of indentation problems are discussed. In the problems probing elastic isotropic materials, the effective contact elastic modulus (E*) is usually estimated either using the unloading branch of the P–δ curve, assuming that the material deforms elastically at unloading and employing the so-called BASh formula (Bulychev, Alekhin, Shorshorov, & Ternovskii, 1976; Bulychev, Alekhin, Shorshorov, Ternovskii, & Shnyrev, 1975), or from the initial elastic stage of the P–δ diagram when the material is loaded by spherical indenters. These estimations are obtained by disregarding the effects of molecular adhesion and using the formulae of the Hertz contact theory or their modifications. Some possible modifications of the BASh formula are studied. The advantages and drawbacks of the above approaches are also discussed.
Most parts of the above mentioned analysis and the theoretical justification of the BASh formula were produced assuming that the indenter is axisymmetric and the material is linearly isotropic. Ifthe indenter is neither a sphere nor a cone, but is either a Vickers or a Berkovich indenter whose tip is a nominally four-sided or a three-sided pyramid, respectively, then the axisymmetric contact solutions are not valid. Also, many well-established techniques are not valid when the tested material is of general anisotropy. I believe that methods of self-similarity are well suited to handling the nonlinear three-dimensional (3D) Hertz-type contact problems. This is because the classic nonlinear Hertz-type contact problems are often self-similar (Borodich, 1983, 1988b, 1989, 1993a; Galanov, 1981a, 1981b, 1982, 2009). If one assumes that the loading at any point of the material is progressive during the contact process, then the elastic–plastic material can be treated as physically nonlinear elastic material (the difference in the material behavior will appear at the points of nonprogressive loading, i.e., at the points of local unloading of the material). The self-similar approach can be applied to many nonlinear materials, and it is very useful for describing the loading (e.g., elastic–plastic branch of the P–δ diagram) when the contact solutions for linear elastic materials are not applicable.
The conditions under which Hertz-type contact problems possess classic self-similarity are as follows (Borodich, 1988b): The constitutive relationships are homogeneous with respect to the strains or the stresses and the indenter’s shape is described by a homogeneous function whose degree is greater than or equal to unity. It is also assumed that during the contact process, the loading at any point is progressive. If the 3D Hertz-type contact problem is self-similar, then it can be considered as a steady state. Indeed, the current state of the contact problem can be characterized by an external parameter (P![]() ), e.g., the compressing force (P). Using a known solution to the self-similar problem for only one value of the parameter P
), e.g., the compressing force (P). Using a known solution to the self-similar problem for only one value of the parameter P![]() , one can obtain the solution for any other parameter value by simple renormalization of the known solution. It is argued that indenters having some deviation from their nominal shapes can be well approximated by nonaxisymmetric monomial functions of the radius. In this case the Hertz-type contact problems obey the self-similar laws. Using similarity considerations of 3D contact problems (Borodich, 1989, 1993a), one can derive the fundamental rescaling relations for the depth of indentation, size of the contact region, load, hardness, and contact area, which are valid for both linear and nonlinear, isotropic and anisotropic materials for various boundary conditions within the contact region (see, e.g., Borodich, Keer, & Korach, 2003; Choi & Korach, 2011). These rescaling formulae are especially important for shallow indentation (usually less than 100 nm), where the tip bluntness is on the same order as the indentation depth.
, one can obtain the solution for any other parameter value by simple renormalization of the known solution. It is argued that indenters having some deviation from their nominal shapes can be well approximated by nonaxisymmetric monomial functions of the radius. In this case the Hertz-type contact problems obey the self-similar laws. Using similarity considerations of 3D contact problems (Borodich, 1989, 1993a), one can derive the fundamental rescaling relations for the depth of indentation, size of the contact region, load, hardness, and contact area, which are valid for both linear and nonlinear, isotropic and anisotropic materials for various boundary conditions within the contact region (see, e.g., Borodich, Keer, & Korach, 2003; Choi & Korach, 2011). These rescaling formulae are especially important for shallow indentation (usually less than 100 nm), where the tip bluntness is on the same order as the indentation depth.
In the classic Hertz-type contact problems, it is assumed that the shape of the bodies and the compressing force P are given and effects of molecular adhesion are disregarded. Therefore, it is assumed that the fields of displacements and stresses appear in the solids only after the external load is applied. However, molecular adhesion is a very important phenomenon at the nanometer scale, and the solids can interact with each other even if the external load is not applied. The traditional BASh approach does not take into account intermolecular interactions between surfaces, while they have to be taken into account when the adhesive forces become significant. Hence, we consider here not only the traditional Hertz-type contact problems but also the mechanics of adhesive contact, and connections of the adhesive contact problems to problems of nanoindentation are discussed. The adhesive contact problems are mainly studied here in the framework of the Johnson–Kendall–Roberts (JKR) theory, which is an extension of the classic Hertz problem of contact between isotropic elastic spheres to the case of contact with adhesion (Johnson, Kendall, & Roberts, 1971). The energy ideas introduced by Derjaguin (1934b) and the Derjaguin approximation are also studied. Although the models of both Sperling (1964) and Johnson et al. (1971) of adhesive contact were based on these energy ideas and the formulae derived by Sperling (1964) are formally the same as the formulae derived independently by Johnson et al. (1971), their approaches were not the same. Here we use mainly the frictionless JKR approach because in my opinion the latter based on the Johnson (1958) idea of superposition of stress fields is mathematically more elegant than the approach adopted by Sperling (1964), which was based on the Jung (1950) solution.
The well-established classic theories of adhesive contact that include the JKR (Johnson et al., 1971), Derjaguin–Muller–Toporov (DMT) (Derjaguin, Muller, & Toporov, 1975; see also Maugis, 2000), and Maugis (1992) theories, propose methods to predict the adhesive force between surfaces of isotropic elastic spheres. The Boussinesq–Kendall (Kendall, 1971) model describes adhesive frictionless contact between a flat-ended axisymmetric punch and an elastic half-space. However, the shapes of contacting solids may be more general than spherical or flat ones. The JKR and Boussinesq–Kendall models are particular cases of the problems for monomial punches, when the degree of the punch d is equal to 2 or it goes to infinity, respectively. It is shown that the frictionless JKR model in the range of its applicability may be generalized to the adhesive contact problem for an arbitrary convex, blunt axisymmetric indenter, in particular to the case of the punch shape being described by monomial (power-law) punches of an arbitrary degree. Our generalized model assumes that the tested sample can be described by linear or linearized material having rotational isotropy of its mechanical properties. One may see that the present derivation based on the use of the above-mentioned general theorems on slopes of the P–δ curves is quite straightforward; perhaps it is even shorter than the original derivation by Johnson et al. (1971).
The derivation of the main formulae of the JKR and Boussinesq–Kendall models is based on the assumption that the material points within the contact region can move along the punch surface without any friction. However, it is more natural to assume that a material point that came into contact with the punch sticks to its surface, i.e., to assume that the nonslipping (no-slip) boundary conditions are valid. Hence, the generalized problems for monomial punches are studied not only under frictionless but also under nonslipping boundary conditions (often these conditions are also referred to as adhesive). It is shown that in the case of power-law-shaped indenters, regardless of the boundary conditions, the solutions to the problems are reduced to the same dimensionless relations between P, δ, and the contact radius a. The explicit expressions for the P–δ and P–a relations are derived for the values of the pull-off force and for the corresponding critical contact radius.
Finally, we discuss methods for experimental determination of the work of adhesion. To apply any theory of adhesive contact and to give quantitative predictions of the adhesive forces, one needs to know both the work of adhesion (w) and the effective contact elastic modulus (K*) of contacting materials. Usually for small material samples, the contact modulus is evaluated by DSI of sharp indenters, while the work of adhesion is determined by direct measurements of the pull-off force of a sphere (see, e.g., Wahl, Asif, Greenwood, & Johnson, 2006). These latter measurements are unstable owing to instability of the load-displacement diagrams at tension, and they can be greatly affected by roughness of contacting solids. Hence, several methods for determination of the work of adhesion (surface energy) of a sample are discussed. It is noted that to solve the inverse problems one needs not only to have a good theoretical model of contact mechanics for interpretation of data but one also needs to overcome difficulties caused by various uncertainties in measurements and the overdeterminate nature of the data obtained from the experiment. It is shown how the work of adhesion and the elastic contact modulus of materials may be quantified by applying the so-called BG method to the results of DSI experiments. The BG method is a nondirect method based on an inverse analysis of a stable region of the experimental force-displacement adhesive curves for a spherical indenter (Borodich & Galanov, 2008). Although this method is under development, it is possible to show that the BG method is simple and robust at least within the range of applicability of the JKR theory. The method can be considered as an alternative to both the BASh method and the direct approach for measuring values of the pull-off force. It is shown here that the BG method allows us to extract w for any solid with rotational symmetry of the elastic properties.
In conclusion, the fracture mechanics approach to the mechanics of adhesive contact is considered. The possibilities for extension of the axisymmetric adhesive contact to 3D case are also discussed.
We will study here only problems using geometrically linearized formulations. This means that we can use the Cauchy stress tensor, the strains are small, and the boundary conditions are given on the nondeformed boundary surface of the solid that is represented as a half-space. If we discuss nonlinear deformations of solids, then this means that we consider physically nonlinear relations, i.e., the Cauchy stresses and strains are connected nonlinearly. Although we will consider here some contact problems for nonlinear elastic solids with homogeneously distributed initial stresses (prestressed solids), the problem formulation will assume that the stresses caused by contact are small in comparison with the initial stresses, and therefore, the small perturbations of strains are superimposed on the large initial strains. Formally, this problem needs to be formulated as a problem of geometrically nonlinear elasticity, however, the problems will be studied on the basis of on linear relations between small perturbations of strains and stresses (for details, see Biot, 1965; Guz, 1986a).
Although this is a review paper, it includes not only published results but also some novel results. For example, it will be shown that many of our results on adhesive contact are valid for materials having rotational symmetry of their elastic properties. These materials include not only isotropic or transversely isotropic elastic solids but also homogeneously prestressed isotropic or transversely isotropic nonlinear elastic materials.
Definitely the present review is not exhaustive. The present paper does not cover many other possible extensions of the classic adhesive contact problems. We do not consider adhesive contact problems for elastic–plastic, viscoelastic, layered, and coated solids (see, e.g., discussions by Barthel, 2008; Johnson & Sridhar, 2001; Kendall, 1971; Olsson & P.-L., 2013; Sergici, Adams, & Muftu, 2006; Shull, 2002). We do not consider either contact problems involving large displacements. The latter class of problems with friction at the contact region were discussed by Curnier, He, and A. (1995). A study of the large deformation mechanics of contact and adhesion between an inflated hyperelastic membrane and a rigid substrate was presented by Long, Shull, and Huia (2010). However, these problems are out of the scope of this paper.
2 The hertz-type contact problems
The Hertz contact theory is well described in many textbooks (see, e.g., Landau & Lifshitz, 1954, 1959; Love, 1893; Rabotnov, 1977). The theory has many areas of application; see, e.g., a review by Adams and Nosonovsky (2000) or a book devoted to contact problems in tribology by Goryacheva (1998). Reviewing papers on solutions to contact problems is out of the scope of this article. One can find good reviews of contact mechanics in books by Galin (1953, 1961, 2008), Gladwell (1980), Johnson (1985), and V. Popov (2010). Hence, we do not discuss various integral forms of general solutions for axisymmetric frictionless contact given by Leonov (1939), Schubert (1942), Harding and Sneddon (1945), Shtaerman (1949) (E.J. Steuermann), and Jung (1950). A quite detailed discussion was given by Argatov and Dmitriev (2003). However, we consider in detail explicit relations among the contact radius, load, and displacement of an arbitrary shaped punch given by Galin (1946).
As mentioned, there is opinion that the current methods of nanoindentation data analysis may lead to incorrect and misleading results; in particular, Chaudhri and Lim (2007) argued that the reduced elastic modulus approach (see formula 3.21) does not work for many indentation experiments. Below we consider the main features of the Hertz-type contact problems.
Let us list here the main assumptions of the original (classic) Hertz contact problem:
1. All components of the strains are small and the higher-order terms are disregarded, i.e., the strain tensors of the large deformation theory are linearized.
2. The material of contacting solids is linearly elastic, i.e., Hooke’s law is valid.
3. The formulation of the boundary value contact problem is geometrically linear and all boundary conditions for contacting solids can be formulated as for elastic half-spaces. This assumption is usually formulated as l ![]() R, where l is the characteristic size of the contact region and R is the characteristic radius of curvature; then each of the solids can be replaced by an elastic half-space.
R, where l is the characteristic size of the contact region and R is the characteristic radius of curvature; then each of the solids can be replaced by an elastic half-space.
4. The contact region G is not known in advance (as will be shown below, this hypothesis will cause the Hertz contact problem to have a specific property: even in the geometrically linear formulation, it is nonlinear with respect to the external parameter of the problem).
5. Only vertical displacements of the boundary are taken into account.
6. There is no friction within the contact region.
7. The initial distance between the surfaces of contacting solids may be approximated as an elliptic paraboloid.
One needs to consider these conditions in detail in order to interpret the indentation experiments using the Hertz approach.
In the Hertz-type contact problem, the assumptions 1, 3-5 of the above classic Hertz contact problem are still valid. However, the materials of the solids may be non-elastic, e.g. materials can be creeping or viscoelastc, and non-linear (this is the case of physical nonlinearity). In addition, the contact problem can be both frictionless and frictional. Finally, there are no restrictions on the initial distance between the surfaces of contacting solids (the shapes may be more general than an elliptic paraboloid; however the above assumptions 1 and 3 should not be violated).
2.1 Formulations of the Hertz-Type Contact Problems
2.1.1 The Hertz Approximation
Let us consider two bodies in contact so that the resultant force between them is P. The contact is only over points, which belong to a small region of the surface of each body. One of the bodies can be considered as absolutely rigid. If the body is rigid, then it is called a punch. Hertz (1882a) considered 3D frictionless contact of two isotropic, linear elastic solids. It is assumed in the classic nonadhesive Hertz problem formulation that two smooth and convex elastic solids initially contact at one point.
Let us use both the Cartesian and the cylindrical coordinate frames, namely, x1 = x, x2 = y, x3 = z and r, φ, z, where r=√x2+y2![]() and x = r cos φ, y = r sin φ. Let us place the origin (O) of the Cartesian x1, x2, x+3 and x1, x2, x−3 coordinates at the point of initial contact between two bodies, and the axes of x+3 and x−3 are directed along normals to the two bodies drawn toward the inside of each (Love, 1893). Let us assume that axis x1 and axis x2 are the same for both bodies.
and x = r cos φ, y = r sin φ. Let us place the origin (O) of the Cartesian x1, x2, x+3 and x1, x2, x−3 coordinates at the point of initial contact between two bodies, and the axes of x+3 and x−3 are directed along normals to the two bodies drawn toward the inside of each (Love, 1893). Let us assume that axis x1 and axis x2 are the same for both bodies.
The quantities referring to the body x+3 ≥ 0 are denoted by a superscript plus sign, and those referring to the second body are denoted by a superscript minus sign. Then the surfaces are described by the shape functions f+ and f−, respectively, i.e.,
x+3=f+(x1,x2),x−3=f−(x1,x2).
where the common tangent plane at O is taken as the x1, x2 plane.
If the bodies are in contact with each other, then displacements u+i, u−i and stresses σ+ij, σ−ij are generated. In the general case, if a body is blunt, this means that the contact problem can be considered in a geometrically linear formulation and the boundary value problem is formulated for a positive half-space, i.e., each of the solids is considered as a half-space.
Let us consider two points m+ and m−, one on each surface, that initially were not in contact and having the same coordinates (x1, x2). A very important assumption of the Hertz contact problem is that only the vertical displacements u−3 and u+3 of the boundaries are taken into account, while displacements u−1, u−2, u+1, and u+2 are disregarded. This means that if the points m+ and m+ contact with each other after application of the load, then the following geometrical condition has to be satisfied:
u+3(x1,x2)=δ−−f−(x1,x2),u−3(x1,x2)=δ+−f+(x1,x2),
where δ± are the approaches of the distant points of each body toward the contact plane x±3 = 0.
Expression (3.1) can be written as
u+3+u−3=δ−(f++f−),δ=δ++δ−.
Hertz (1882a) described the general shape of a 3D body as an elliptic paraboloid. It follows from the formulation of the problem that f(0, 0) = 0. It is also known that the first derivatives of a smooth function at an extremum (in our case at a maximum) of the function are zero. If a decomposition of f+ and f− into a Taylor series is not degenerative for second terms, then the truncated decomposition can be written as
z+=(A+x21+B+x22+2C+x1x2),z−=(A−x21+B−x22+2C−x1x2),
where A±, B±, and C± are constants of the decompositions. Substituting Eq. (3.3) into Eq. (3.1), one gets
u+3+u−3=δ−[(A++A−)x21+(B++B−)x22+2(C++C−)x1x2].
After rotating axis x1 and axis x2 into the properly chosen axes x and y, one can rewrite Eq. (3.4) as
u+3+u−3=δ−Ax2−By2.
Thus, it was assumed in the classic Hertz formulation that the shape function f is described as an elliptic paraboloid. The equation z+ + z− = const describes a curve within the xy plane such that all points of the curve correspond to the same height. Hertz (1882a) showed that the contact region for contacting solids whose shape is described by Eq. (3.3) can be described by z+ + z− = Ax2 + By2 = const and the region is an ellipse.
2.1.2 The Hertz-Type Boundary Value Problem
It is supposed that the shape of the punch f and the external parameter of the problem P![]() are given and one has to find the bounded region G on the boundary plane x3 = 0 of the half-space at the points where the punch and the medium are in mutual contact, displacements ui, and stresses σij. If the pressing force P is taken as the external parameter P
are given and one has to find the bounded region G on the boundary plane x3 = 0 of the half-space at the points where the punch and the medium are in mutual contact, displacements ui, and stresses σij. If the pressing force P is taken as the external parameter P![]() , then one has to find the depth of indentation δ and the characteristic size of the contact region l. If δ is taken as P
, then one has to find the depth of indentation δ and the characteristic size of the contact region l. If δ is taken as P![]() , then one has to find P and l.
, then one has to find P and l.
In the general case of a 3D Hertz-type contact problem, it is not assumed that the punch shape is described by an elliptic paraboloid and the contact region is an ellipse as Hertz (1882a) did. The Hertz-type contact problems mean that the formulation of the problem is geometrically linear, the contact region is unknown, only vertical displacements of the boundary are taken into account, and we have the same boundary conditions within and outside the contact region as in classic Hertz contact problems (Hertz, 1882a). Hence, one must find the finite region G of the points at which the bodies are in mutual contact, the relative approach of the bodies δ > 0, the displacements u+i and u−i, and the stresses σ+ij and σ−ij.
One can see from Eq. (3.1) that the problem formulation is mathematically equivalent to the problem of contact between a positive half-space and an indenter whose shape function f is equal to the initial distance (the gap) between the surfaces, i.e., f = f+ + f−. As we will see, this problem, in turn, can be reduced to the problem of contact between a rigid indenter (a punch) and an elastic half-space with effective elastic constants. For the sake of simplicity, let us consider the case when a rigid punch is pressed by the force P into the positive half-space x3 ≥ 0. The quantities sought must satisfy the following:
σij,j=0,i,j=1,2,3;
2. constitutive relations
σij=F(εij),εij=(ui,j+uj,i)/2;
3. conditions at infinity
u(x,P)→0,|x|→∞;
4. integral condition
∫R2σ33(x1,x2,0,P)dx1dx2=−P;
5. boundary conditions outside the contact region G(P)![]()
σ3j(x1,x2,0,P)=0,(x1,x2)∈R2G(P);
6. three boundary conditions within the contact region G(P).
Here and henceforth, a comma before the subscript denotes the derivative with respect to the corresponding coordinate; and summation is assumed over repeated Latin subscripts that take values from 1 to 3, while there is no summation over repeated Greek subscripts that take values from 1 to 2.
The contact region G is defined as an open region such that if x ∈ G, then the gap (u3 − g) between the punch and the half-space is equal to zero (see Eq. 3.2) and surface stresses are nonpositive, while outside the contact region, i.e., for x∈R2G![]() , the gap is positive and the stresses are equal to zero. This can be written as
, the gap is positive and the stresses are equal to zero. This can be written as
u3(x;P)=g(x;P),σ33(x;P)≤0,x∈G(P),u3(x;P)>g(x;P),σ3i(x;P)=0,x∈R2G(P).
For the general case of the problem of vertical pressing, we have
g(x;P)=δ(P)−f(x1,x2).
The choice of two other conditions (3.13), (3.14), or (3.15) depends on the friction within the contact region.
Remarks.
1. The above formulations are also valid for time-dependent materials. For such materials, one should add the variable t to the arguments of all functions, e.g., one should write write u(x,t,P)![]() instead of u(x,P)
instead of u(x,P)![]() .
.
2. Depending on the form of the operator of constitutive relations F in Eq. (3.7), the material behavior of the medium may be anisotropic or isotropic, and linear or nonlinear with different rheological properties.
2.1.3 The Types of Contact Boundary Conditions
It is supposed that σ33(x,P)≤0![]() when x∈G(P)
when x∈G(P)![]() . Then depending on the frictional conditions within the contact region, the problem can be frictionless, nonslipping (it is also called “adhesive”), or frictional (Johnson, 1985).
. Then depending on the frictional conditions within the contact region, the problem can be frictionless, nonslipping (it is also called “adhesive”), or frictional (Johnson, 1985).
In the frictionless problem, these conditions can be written as
σ±31(x1,x2,0,P)=σ±32(x1,x2,0,P)=0,(x1,x2)∈G(P).
In the nonslipping contact problem, there is no relative slip between the bodies within the contact region. If the values
v1(x1,x2,P)≡u+1(x1,x2,0,P)−u−1(x1,x2,0,P)
and
v2(x1,x2,P)≡u+2(x1,x2,0,P)−u−2(x1,x2,0,P)
are introduced, then the condition within this region is that these values do not change with augmentation of the external parameter P![]() . These conditions of no relative slip can be expressed by
. These conditions of no relative slip can be expressed by
∂∂Pvα(x1,x2,P)=0,dP>0.
In the frictional contact problem, it is usually assumed (Bryant & Keer, 1982; Galin, 1945) that the contact region consists of the following parts: the inner part G1, in which the interfacial friction must be sufficient to prevent any slip taking place between bodies, i.e., Eq. (3.14) holds; the outer part G G1, in which the friction must satisfy the Amontons–Kotelnikov (or Coulomb) frictional law (in fact, Amontons (1699) gave a verbal formulation of the law as three relations observed for an optical lens polishing process, while Kotelnikov (1774) introduced the notion of the coefficient of friction and presented the law as a formula).
Let us define the vector of tangential stresses:
τ±(x1,x2,0,P)≡(σ±31(x1,x2,0,P),σ±32(x1,x2,0,P)).
If μf is the coefficient of friction, then the frictional contact conditions can be written as (Spektor, 1981; Vermeulen & Johnson, 1964)
∂∂Pvα(x1,x2,P)=0,dP>0,(x1,x2)∈G1,τ±(x1,x2,0,P)=−μfσ±33(x1,x2,0,P)[v(x1,x2,P)|v(x1,x2,P)|],(x1,x2)∈GG1,
where v(x1,x2,P)=(v1(x1,x2,P),v2(x1,x2,P))![]() .
.
In addition to the above formulations of the Hertz-type contact problems, sometimes a more general formulation of the axisymmetric mixed boundary value contact problems is considered. In the general formulation (see, e.g., G. I. Popov, 1973), it is assumed that in the system subjected to a normal contact force P, the displacements ur(r,0,P)![]() and uz(r,0,P)
and uz(r,0,P)![]() are known within the contact region, and the solids are not loaded outside the contact region, i.e.,
are known within the contact region, and the solids are not loaded outside the contact region, i.e.,
ur(r,0,P)=s(r),uz(r,0,P)=g(r),forr≤a;
σrz(r,0,P)=σzz(r,0,P)=0,forr>a;
where s(r) and g(r) are known functions of the radial and normal displacements, respectively. The condition for the given radial displacements ur(r,0,P)![]() can be reformulated as the condition for mismatch strain distributions ε(r) between the contact surfaces (Guo, Jin, & Gao, 2011).
can be reformulated as the condition for mismatch strain distributions ε(r) between the contact surfaces (Guo, Jin, & Gao, 2011).
2.1.4 The Harmonic Function Formulation of the Frictionless Problem
It is well known (see, e.g., Galin, 1961, 2008; Rabotnov, 1977) that the components of the displacement vector u in a linear elastic solid can be expressed through four harmonic functions. This is the so-called Papkovich–Neuber representation. Further, if all tangential stresses σ3α on the boundary plane of a linear elastic half-space are equal to zero, then all displacements and stresses can be represented by a single harmonic function Φ (see, e.g., Galin, 1961; Rabotnov, 1977), i.e., δΦ = 0, where δ is the Laplace operator:
Δ=∂2∂x2+∂2∂y2+∂2∂z2.
In this case one has
u3=2(1−v)Φ(x,y,0),σ33=E1+v∂Φ(x,y,0)∂z.
Thus, the boundary conditions of the contact problem can be expressed in terms of the harmonic function Φ: one knows the function within the contact region G, while its normal derivative is given on the rest of the half-space boundary:
Φ(x,y,0)=w(x,y)2(1−ν),(x,y)∈G;∂Φ(x,y,0)∂z=−(1+ν)p(x,y)E,(x,y)∈R2G;
where w and p are normal displacements and pressure given within and outside the contact region G, respectively. Hence, the contact problem is a mixed boundary value problem for a harmonic function Φ.
If a normal pressure p(x1, x2) is applied only to the finite region G, then the harmonic function Φ can be written as the so-called single layer potential (see, e.g., Galin, 2008)
Φ(x,y,z)=12π∫∫Gp(ξ,η)dξdη√(x−ξ)2+(y−η)2+z2,
and one has
u3(x,y,0)=1πE*∫∫Gp(ξ,η)dξdη√(x−ξ)2+(y−η)2,
where E* = E/(1 − ν2) is the reduced elastic modulus.
If one considers contact of two elastic solids, then
u+3(x,y,0)=1−(ν+)2πE+∫∫Gp(ξ,η)dξdη√(x−ξ)2+(y−η)2
and
u−3(x,y,0)=1−(ν−)2πE−∫∫Gp(ξ,η)dξdη√(x−ξ)2+(y−η)2.
Substituting the above expressions into Eq. (3.2), one obtains
δ−(f++f−)=1πE*∫∫Gp(ξ,η)dξdη√(x−ξ)2+(y−η)2,
where the reduced elastic modulus is
1E*=1−(ν+)2E++1−(ν−)2E−.
If the indenter is rigid, i.e., E− = ∞, then E* = E/(1 − ν2), where E = E+ and ν = ν+ are the elastic modulus and the Poisson ratio of the half-space, respectively.
It follows from the above consideration that the frictionless Hertz-type contact problem reduces to the problem of determination of the pressure distribution satisfying Eq. (3.20).
2.1.5 Incompatibility of the Hertz-Type Problem Formulations
One needs to be aware that the Hertz formulation of the contact problems leads to incompatibility of displacement fields. There are two types of incompatibility of the contact problems: (1) penetration of the upper material layer into the lower one owing to the geometrically linear formulation of the problem; (2) penetration of the material into the punch owing to the disregarding of the tangential displacements in the formulation of the Hertz-type contact problems (see, e.g., Borodich, Galanov, & Suarez-Alvarez, 2014; Rvachev & Protsenko, 1977).
Considering the classic Boussinesq problem for a concentrated load and the Abramov (1937) problem for a two-dimensional (2D) nonslipping contact between a flat punch and an isotropic linear elastic half-space, Rvachev and Protsenko (1977) discussed both types of incompatibility. To avoid or at least to reduce the incompatibility, one needs to employ the geometrically nonlinear formulation of the contact problem that includes the Signorini–Fichera conditions of impenetrability of the material points (Fichera, 1972; Signorini, 1933) along with accounting for the boundary tangential displacements (Kindrachuk & Galanov, 2014; Kindrachuk, Galanov, Kartuzov, & Dub, 2009).
Contact problems with the conditions of impenetrability linearized with respect to boundary tangential displacements were studied by Galanov (1983) and Galanov, Krivonos (1984a). If one takes into account the conditions of impenetrability
uz(r,0,P)−δ+f[r+ur(r,0,P)]≥0,
then instead of Eq. (3.12) in the first condition Eq. (3.11), the following one has to be written:
uz(r,0,P)−δ+f[(r+ur(r,0,P)]=0.
The above equation is normally nonlinear; hence, the condition within the contact region can be linearized with respect to ur and can be written as
uz(r,0,P)−δ+f(r)+L(r)ur(r,0,P)=0,
where L(r) is obtained by linearization of f with respect to ur.
As an attempt to reduce the degree of this incompatibility, Galanov (1983) considered a refined formulation of the Hertz-type contact problem when lateral displacements are taken into account. It was shown that the use of this more rigorous formulation than the Hertzian one substantially reduces the degree of the displacement incompatibility observed at the contact region and under the region. The contact problem with the nonlinear boundary condition (3.22) was studied by Galanov and Krivonos (1984b). A formulation of unilateral contact between two deformable continuous solids undergoing large displacements with friction at the interface was presented by Curnier et al. (1995).
2.2 Solutions to Frictionless Contact Problems
2.2.1 The Classic 3D Hertz Solution
Using a known expression for the potential of an ellipsoid, Hertz (1882a) solved the isotropic linear elastic contact problem (3.20) for an elliptic paraboloid, and showed that the contact region is an ellipse with semiaxes a and b. He wrote condition (3.5) as
δ−Ax2−By2=3P4πE*∞∫01−x2a2+k−y2b2+k√k(a2+k)(b2+k)dk,
which can be split into three equation for δ, a, and b. Hertz solved the equations explicitly.
Boussinesq (1885) noted that to get a unique solution for the unknown contact region, the normal component of stress in the frictionless Hertz-type contact problems must be equal to zero at the border line of the contact region. This condition gives the depth of indentation δ of the convex punch; another value δ0 of the depth of indentation would correspond to the superposition of the rigid displacement δ − δ0 of the punch and to the corresponding singular stress field at the edge of the contact region. As Maugis and Barquins (1983) commented for this condition, such a superposition was used later by Johnson (1985) and Johnson et al. (1971) to study adhesive contact of spheres.
After careful examination of the Hertz contact problem, it was shown by Dinnik (1952) in 1908 for a circular contact region and in 1917 by Belyaev (1924) for an elliptic contact region that the point of maximum shearing stresses and consequently the point of first yield in the Hertz contact theory are beneath the contact surface. A very useful analysis of the Hertz problem was presented by Sackfield and Hills (1983).
We will not present the Hertz solution here. It is important for us that the following power law expressions for the a–P and δ–P relations can be derived:
a=C1P1/3,δ=C2P2/3,
where C1 and C2 are constants that may be derived explicitly using the Hertz solution.
Shtaerman (1941) solved the contact problem for an indenter that was closer to the surface than the Hertzian punch, i.e., he considered not f = Ax2 + By2 as Hertz did but f = (Ax2 + By2)2. It follows from the Shtaerman solution that
a=C3P1/5,δ=C4P/a=C5P4/5,
where C3, C4, and C5 are constants that were derived explicitly by Shtaerman (1941).
2.2.2 Dimensional Analysis of Anisotropic Problems
Note that the Hertz equation (3.24) and the corresponding solutions are also valid not only for isotropic linear elastic materials but also for some anisotropic and nonlinear prestressed materials described by linearized models.
The mechanics of anisotropic elastic materials is a quite developed research field (see, e.g., Lekhnitskii, 1981; Ting, 1996). The contact problems for anisotropic solids were studied in many papers. However, as Willis (1966) noted, it is difficult to expect to obtain an analytical solution to the contact problems for generally anisotropic solids except for transversely isotropic materials. For arbitrary anisotropic, linear elastic media, the constitutive relations have the form of Hooke’s law:
σij=cijklεklorσij=cijkluk,l,cijkl=cijkl=cklij,
where cijkl are components of the tensor of elastic constants.
With use of dimensional analysis, it can easily be shown (Borodich, 1990e) that the displacement of any surface point of an anisotropic linear elastic half-space under the influence of a point load P is proportional to the ratio, P/r, where r is the distance to the point of the application of the load. Indeed, the central theorem of dimensional analysis or the Π theorem says (see, e.g., Barenblatt, 1996):
If a physical law is written as a relationship between some dimensional quantity and several dimensional governing parameters, then
– it is possible to rewrite this relationship as a relationship between some dimensionless parameter and several dimensionless products of the governing parameters;
– the number of dimensionless products is equal to the total number of the governing parameters minus the number of governing parameters with independent dimensions.
Let a concentrated force P be applied normally to the surface of the half-space at the point 0, i.e., it is directed along the z axis. If the material of the half-space is linear elastic anisotropic with Hooke’s law (3.27), then this is the Boussinesq problem for a concentrated load acting on an anisotropic elastic half-space.
Let us apply the Π theorem. The normal displacements (u3) at points of the boundary are given by
u3=Φu(P,r,ɸ,cijlm),
where Φu is some functional relation. For the physical dimensions of the governed and the governing parameters, one can write
[u3]=L,[r]=L,[P]=F,[ɸ]=1,[cijlm]=FL−2,
where L and F denote the physical dimensions of length and force, respectively. In the above case, the number of governing parameters (n) is 24 because there are 21 independent components of the tensor cijlm. The first two governing parameters have independent dimensions, and [u3/r] = 1. Hence, the number of governing parameters with independent dimensions (k) is two, and n − k = 22, and we have the following dimensioniess parameters
Π=u3r,Π1=Pc1111r2,Π2=ɸ,Πp=cijlmc1111,p=3,…,22,
and we have
Π=Φ1(Π1,Π2,Πp).
The problem is not axially symmetric because of anisotropy of the material. Taking into account that the problem is linear, one obtains
Π=Π1Φ2(Π2,Πp)oru3=Prc1111Φ2(φ,cijlmc1111).
In particular, if the half-space is isotropic, then there are only two elastic constants [E] = FL−2 and [ν] = 1. In addition, the problem is axially symmetric because of isotropy of the material. Hence, Φ2 is independent of Π2 and one has the known result
u3=PErΦ2(ν).
If we solved the problem exactly, then we could see that Φ2(ν) = (1 − ν2)/(π). The detailed expression for the Green’s function for an anisotropic elastic half-space can be found in Vlassak and Nix (1994).
Using dimensional arguments similar to the ones above, let us consider the Boussinesq relation for a flat-ended cylindrical indenter of radius a contacting an arbitrary anisotropic elastic half-space. Assuming that the base is horizontal and the total load is P, one immediately obtains the following relation for the depth of indentation (see, e.g., Borodich, Galanov, Keer, & Suarez-Alvarez, 2014):
δ=Pac1111Φc(cijklc1111),
where Φc is a function of the dimensionless elastic material constants.
Willis (1966, 1967) obtained much more detailed results. He studied both Hertzian and Boussinesq contact problems for anisotropic bodies and showed that the functional form of the pressure distribution between the contacting bodies can be found explicitly, and therefore the problem is reduced to finding the displacements due to a pressure distribution of this form. With use of these results, the JKR theory was extended to transversely isotropic elastic materials (Borodich, Galanov, Keer, & Suarez-Alvarez, 2014; Espinasse, Keer, Borodich, Yu, & Wang, 2010).
2.2.3 Solutions for Transversely Isotropic Materials
Transverse isotropy is a very important case of anisotropy because many natural and artificial materials behave effectively as transversely isotropic elastic solids. For example, modern tribological coatings or layered composite materials can often be described as having transversely isotropic properties. Various problems and approaches to the mechanics of transversely isotropic materials were discussed in Ding, Chen, and Zhang (2006). Numerous papers have been devoted to the study of various problems of mechanics for transversely isotropic materials (see, e.g., Kaplunov, Kossovich, & Rogerson, 2000; Kuo & Keer, 1992; Lekhnitskii, 1940), in particular to contact and indentation problems (see, e.g., Argatov, 2011; Borodich, 1989; Delafargue & Ulm, 2004). Referring to Sveklo (1964), Willis (1966) argued that in the case of transversely isotropic materials, the Hertz-type contact problem can be reduced to one of potential theory. Green and Zerna (1968) also showed the similarities between isotropic and transversely isotropic frictionless 2D indentation problems. A similar result was presented earlier by Lekhnitskii (1940, 1981), who computed the stresses in the interior of a transversely isotropic half-space loaded by a normal concentrated load. Independently of Willis, Conway, Farnham, and Ku (1967) presented an analytical expression for the solution for the frictionless Hertz-type contact between transversely isotropic solids using the results obtained by Lekhnitskii (1940, 1981).
To describe the general anisotropy of elastic solids, the tensor of elastic constants cijkl has been used; however, the matrix form is more convenient for the description of transversely isotropic solids. This is because the tensor of elastic constants is reduced to five elastic constants of the material: a11, a12, a13, a33, and a44. Let the z axis be taken normal to a plane of isotropy, i.e., the z axis is the axis of rotational symmetry, then Hooke’s law (3.27) becomes
(ε11ε22ε33ε12ε13ε23)=(a11a12a13000a12a11a13000a13a13a33000000a11−a1200000a44/2000000a44/2)(σ11σ22σ33σ12σ13σ23).
In cylindrical coordinates Hooke’s law for a transversely isotropic elastic material becomes
(εrrεɸɸεzzεrɸεrzεɸz)=(a11a12a13000a12a11a13000a13a13a33000000a11−a1200000a44/2000000a44/2)(σrrσɸɸσzzσrɸσrzσɸz)
or
(σrrσɸɸσzzσrɸσrzσɸz)=(A11A12A13000A12A11A13000A13A13A33000000A11−A12000002A440000002A44)(εrrεɸɸεzzεrɸεrzεɸz),
where A11, A12, A13, A33, and A44 are five elastic constants of the material,
A11=a11a33−a213(a11−a12)m,A12=a213−a12a33(a11−a12)m,A13=−a13m,
A33=a11+a12m,A44=1a44A11−A12=1a11−a12,
and
m=(a11+a12)a33+2a213.
Using the above expressions and the results obtained by Lekhnitskii (1940, 1981), one can show that the solution of the Boussinesq problem for a concentrated load P is
u3(r,0)=PπETIr,
where the coefficient (ETI)−1 is
(ETI)−1=−S1+S22D1/2(AC−D)[(D−2BD+AC)a11−(2D−BD−AC)a12]
and
A=a13(a11−a12)a11a33−a213,B=a13(a13+a44)=a12a33a11a33−a213,C=a13(a11−a12)=a11a44a11a33−a213,D=a211−a212a11a33−a213,2DS21,2=A+C±[(A+C)2−4D]1/2,S1,2=√A+C2D±[(A+C2D)2−1D]1/2.
For isotropic materials ETI is equal to E*.
Thus, one can write a general equation for the pressure distribution under an indenter acting on a linear elastic half-space having rotational symmetry of its elastic properties,
u3(x,y,0)=1πK*∫∫Gp(ξ,η)dξdη√(x−ξ)2+(y−η)2,
that is the same up to a constant as the pressure distribution within an isotropic linear elastic half-space. It follows from the above consideration that one needs just to replace the reduced elastic modulus E* in Eq. (3.19) by K* = ETI (do not confuse the modulus K* with the modulus K = (4/3)E* of an isotropic elastic material).
2.2.4 Solutions for Prestressed Materials
Nowadays indentation techniques are often applied to biological and/or prestressed nonlinear materials (see, e.g., Kendall, Kendall, & Rehfeldt, 2011; Scherge & Gorb, 2001; Sen, Subramanian, & Discher, 2005; Yang, 2004). Information concerning mechanical problems for homogeneously deformed nonlinear elastic solids can be found elsewhere. For example, Biot (1965), Eringen and Suhubi (1975), and Guz (1986a, 1986b) gave detailed descriptions of static and dynamic problems for prestressed elastic media. Usually various potential functions are used to describe the stress–strain relations in nonlinear materials. These include harmonic, Mooney-Rivlin, Treloar (neo-Hookean solid), Bartenev-Khazanovich, and other potentials (see, e.g., Babich, Guz, & Rudnitskii, 2004; Guz, 1986a). The equations of the theory of nonlinear elasticity may be written using a variety of stress and strain tensors, and linearized equations for bodies with initial stresses may be also written in a variety of forms. A comprehensive review of current state-of-the-art research in the area of contact problems for prestressed solids was presented by Babich et al. (2004). They noted that the overwhelming number of authors writing about contact problems for prestressed solids assume (1) first the elastic solid is prestressed and then comes into contact with a punch, (2) the stress field due to the contact is just a small perturbation of the large initial stresses, (3) the initial stress field can be considered as homogeneous, and (4) the linearized elastic contact problem has a unique solution.
Let σij(x) be components in the Cartesian system of coordinates of the nonsymmetric stress tensor σ, linearly related to the components of the Kirchhoff stress tensor. The components of σ are related to the area units in the initial static stress state. The component σnl is the lth component of the stress vector σn acting on the positive side of the coordinate surface with the nth component of the normal, i.e., σn = σnlil. The vector u is the vector of the small perturbations of the displacements and il is the unit basis vectors.
For homogeneously prestressed elastic solids, the linearized constitutive relations and the equations of equilibrium can be written as (Guz, 1986a, 1986b)
σij=ω*ijkl∂uk∂xl,ω*ijkl∂2uk∂xixl=0.
Here ω*ijkl are the components of the proportionality between the small perturbations of the stresses and deformations, which, in the general case, have lesser symmetry properties than the tensor Cijkl of anisotropic linear elasticity: ω*ijkl = ω*lkji, ω*ijkl ≠ ω*ijlk, ω*ijkl ≠ ω*klij.
A 2D contact problem for a prestressed plane whose elastic properties are described by the Mooney potential was solved in a pioneering paper by Filippova (1973). Later she extended her results to 3D solids (Filippova, 1978) and considered contact problems for incompressible materials of the neo-Hookean type:
W=12μ(λ21−1+λ22−1+λ23−1),
where W is the Treloar potential, μ is the Lamé constant, which is equal to the shear modulus when the deformations are small (the shear modulus μ = E/2(1 + ν)), and λi is the extension ratio in the xi direction. Because the material is incompressible, one has
λ1λ2λ3=1.
Filippova (1978) considered not only the case of homogeneously prestressed solids (λ1 = λ2), but also the case λ1 ≠ λ2. She noted also that in the case when the initial extensions are the same in both directions (λ1 = λ2 = λr = λ), the solution of the Boussinesq problem for a concentrated load P is
u3(r,0)=P4πμrNF(λ),
where
NF(λ)=2λ4(1+λ3)λ9+λ6+3λ3−1.
Because for incompressible solids ν = 0.5, one has
u3(r,0)=PπE*rNF(λ).
Hence, the integral equation of an arbitrary contact problem for equally and uniformly prestressed solids differs from the integral equation of the corresponding classic contact problem only by a constant coefficient N(λ) = NF(λ).
Practically simultaneously with the publication of the above-mentioned paper, Dhaliwal and Singh (1978) considered axisymmetric contact problems for uniformly prestressed neo-Hookean solids. Their solution was based on the paper by Sneddon (1965), who considered classic axisymmetric contact problems (see above). Dhaliwal and Singh (1978) noted that the contact problem solution has to be multiplied by a coefficient that depends on the initial tension (compression). They presented the following coefficient:
NDS=−21−k2λ2z[(1+k2)2−4k],
where k = λr/λz.
Let us show that the coefficient NDS introduced by Dhaliwal and Singh (1978) and the coefficient NF(λ) introduced by Filippova (1978) are the same. If the initial extensions are the same in the x1 and x2 directions, then it follows from the condition of incompressibility (Eq. 3.38) that k = λ3 and λz = λ−2. Substituting these values into Eq. (3.40), one obtains
NDS(λ)=−2(1−λ6)λ4(1+λ6)2−4λ3=−2(1−λ6)λ4λ12+2λ6−4λ3+1
or
NDS(λ)=−2λ4(1−λ3)(1+λ3)−(1−λ3)(λ9+λ6+3λ3−1)=NF(λ).
Babich and Guz (1984) showed that all Hertz-type contact problems for contact between a punch and a nonlinear elastic homogeneously prestressed half-space coincide with the mixed problem for the harmonic potential of the contact problem for an isotropic linear elastic half-space up to a constant multiplier. Babich et al. (2004) gave examples of the multipliers for other potentials of nonlinear materials, e.g., (1) for a nonlinear material with the harmonic potential
N(λ)=NH=λ22+ν(λ−1+ν2+ν)−1,
and (2) for a nonlinear material with the Bartenev-Khazanovich potential
N(λ)=NBK=2λ7/2(3λ3−1)−1.
The effective contact modulus EPS for a nonlinear elastic homogeneously prestressed half-space is EPS = E*/N(λ), where N(λ) depends on the initial deformations λ within the xy plane and the nonlinear strain potential of the material.
Thus, Eq. (3.37) is still valid for homogeneously prestressed solids if one takes K* = EPS. As noted by Borodich (1990a), if one considers contact between a transversely isotropic indenter and a prestressed half-space, then Eq. (3.37) is still valid; however (K*)−1 = (ETI)−1 + (EPS)−1.
I would like to repeat that the materials of all the above-considered frictionless Hertz-type contact problems that are reduced to the mixed problem for the harmonic potential with an appropriate effective modulus K* have rotational symmetry of their elastic properties. I will use the effective modulus K* in all frictionless problems of this type without further explanations that the results obtained are applicable to all these materials having rotational symmetry of the properties.
2.2.5 Axisymmetric Frictionless Contact
In the problem of vertical indentation of a medium with rotational symmetry of the elastic properties by an axisymmetric punch, the contact region is always a circle. This fact simplifies analysis of the problem.
Boussinesq (1885) solved the problem of contact between a flat-ended circular punch and an elastic half-space. The Boussinesq relation for a flat-ended cylindrical indenter of radius a is
P=2E1−v2aδ≡2K*aδ.
In 1939 two very important results were presented. Love (1939) considered the Boussinesq problem for a rigid cone f(r) = B1r of the included semi-vertical angle α. The formulation of the Love problem was similar to the formulation of the frictionless Hertz-type contact problem. It was assumed that the cone over the part between the vertex and a certain circular section of radius a is in contact with the elastic half-space. Then the pressed region is given by r ≤ a at z = 0, and the vertical displacement on the pressed region is given by u3 = δ − r cot α. Love (1939) used the same linearized formulation of the boundary value problem as Hertz and all boundary conditions were formulated for the z = 0 plane. Using this formulation, he obtained
P=π2E*B1a2,δ=π2B1a.
Hence, one has
a=AP1/2,δ=BP1/2,
where A and B are constants that may be derived explicitly using the Love solution (Eq. 3.42).
Although Sneddon was accurate in his citation of early papers of his predecessors, researchers in the materials science community attribute to him many results obtained by other researchers. In particular, it is quite often stated that Sneddon (1948) solved the contact problem for a cone and derived formula (Eq. 3.42).
Shtaerman (1939) presented a solution to the problem of an elastic contact for an axisymmetric solid whose shape is given by a power-law function (a monomial) of even degree
f(r)=B2nr2n,B2n=const,
where B2n is a constant of the shape and the integer degree is given by n ≥ 1.
Thus, many explicit solutions to the frictionless problem for isotropic, linear elastic solids were obtained in the case when the distance between contacting bodies is a homogeneous function. These are solutions obtained by Hertz (1882a) for d = 2, Love (1939) for d = 1, Shtaerman (1939) for d = 2n, Galin (1946) for d = m/n (where m and n are natural numbers), and others. Willis (1966) studied in detail problems for anisotropic, linear elastic solids in the case d = 2.
2.3 Galin’s Solution for Axisymmetric Contact
Using the harmonic function presented by Kochin (1940), Galin (1946) considered axisymmetric frictionless contact problems for an elastic isotropic half-space. He obtained expressions for the contacting force P, the depth of penetration δ, and the pressure distribution under a convex, smooth in R2{0}![]() punch of arbitrary shape
punch of arbitrary shape
x3=−f(r),f(0)=0.
In particular, he wrote (see equations 5.29 and 5.30 in Galin, 1946 or equations 5.29 and 5.30 in Galin, 1953)
P=2E1−ν2∫a0rΔf(r)√a2−r2dr,
and
δ=∫a0rΔf(r)arctanh(√1−r2/a2)dr.
Here a is the radius of contact, and δ denotes the 2D Laplace operator
Δ=∂2∂x21+∂2∂x22=∂2∂r2+1r∂∂r.
The Galin solution (3.46) and (3.47) can be represented in various forms. Let us derive one of them.
Substituting Eq. (3.48) into Eq. (3.46), one has
P2K*=I1+I2,I1=∫a0f″(r)r√a2−r2dr,I2=∫a0f′(r)√a2−r2dr.
Integrating by parts, one obtains
I1=[f′(r)r√a2−r2]a0−∫a0f′(r)d(r√a2−r2)=−I2+∫a0r2f′(r)dr√a2−r2.
Hence, the first Galin relation (3.46) transforms to the following one:
P2K*=∫a0r2f′(r)dr√a2−r2.
Similarly, substituting Eq. (3.48) into Eq. (3.47), one has δ = I3 + I4, where
I3=∫a0rf″(r)arctanh(√1−r2/a2)dr,I4=∫a0f′(r)arctanh(√1−r2/a2)dr.
Integrating by parts, one obtains
I3=[f′(r)rarctanh(√1−r2/a2)]a0−a∫0f′(r)d(rarctanh(√1−r2/a2))=I4−a∫0rf′(r)d(arctanh(√1−r2/a2))
Hence, one has
δ=−a∫0rf′(r)d[arctanh(√1−r2/a2)].
Taking into account the definition (see, e.g., (4.6.3) and (4.6.22) in Abramovitz and Stegun (1964))
arctanhν=∫ν0dt1−t2=12ln1+ν1−ν,
and substituting v=√1−r2/a2![]() into Eq. (3.50), one obtains
into Eq. (3.50), one obtains
d[arctanhν]da=11−ν2r2a−3√1−r2/a2=1√a2−r2.
This leads to the following representation of the second Galin formula:
δ(a)=∫a0f′(r)√1−r2/a2dr.
The above representations were derived by Rostovtsev (1953) and much later independently by Borodich and Keer (2004a), Argatov and Dmitriev (2003). Rostovtsev (1953) introduced a very elegant method based on the use of special harmonic functions of complex variables, and using these functions, he derived formulae (3.49) and (3.52). Argatov and Dmitriev (2003) used the general Leonov–Schubert–Steuermann integral solution as the starting point for their calculations (Leonov, 1939; Schubert, 1942; Shtaerman, 1949). Because materials science community is, in general, not aware of the above results in contact mechanics, it is often stated that Sneddon (1965) was the first to solve an axisymmetric Boussinesq problem for an indenter of arbitrary shape and that Sneddon created a new contact theory (the Sneddon contact theory). In fact, Sneddon always used the above-described geometrically linear frictionless Hertz-type formulation of the contact problems in order to produce a solid mathematical analysis of the problems. Because the formulae presented by Sneddon (1965) are quite similar to Eqs. (3.49) and (3.52), it is clear that such an excellent mathematician could derive them in a few lines from the Galin solution given above, as demonstrated above. However, giving great appraisal to the book by Galin (1953), whose English translation (Galin, 1961) he edited, Sneddon (1965) gave another representation of the Galin solution. Using techniques of Hankel transforms, he attacked the same Boussinesq problem for a punch of arbitrary shape (Eq. 3.45) as Galin did. The Sneddon representation was in terms of w(r) = f(r/a), and his approach was based not on the use of the Kochin harmonic function but rather on the approach by Harding and Sneddon (1945). The novelty of Sneddon (1965) paper is in the use of new mathematical techniques - Hankel transforms. All results related to contact problems were derived by other authors earlier. Indeed, the two formulae he presented in Introduction were derived earlier by Galin (1946) (see the reference [4] by Sneddon) and Rostovtsev (1953). His Section 2 is dedicated to Hankel transforms techniques. Section 3 is dedicated to the derivation of the first Galin formula using the Hankel techniques. Section 4 is dedicated to the derivation of the second Galin formula using the Hankel techniques. Section 5 is dedicated to studies of the shape of the deformed surface - this problem was solved by Leonov (1953a, 1953b) in more general case. Section 6 is dedicated to consideration of particular cases, including the Boussinesq (1885) problem (formula (6.l)) for a flat-ended cylindrical punch (see the reference [1] by Sneddon), the Love (1939) problem (formula (6.4)) for a conical punch (see the reference [3] by Sneddon), the Hertz (1882) problem (formulas (6.9) and (6.10)) for a paraboloid of revolution, the Segedin (1957) problem for a punch in the shape of an ellipsoid of revolution (see the reference [6] by Sneddon), and for a spherical punch that is a particular case of the Segedin problem. As it follows from its title, Section 7 is dedicated to studies of the Segedin (1957) problem for a punch whose shape is represented as a series (see the reference [6] by Sneddon). I would like to add, it is rather often stated that Sneddon (1965) discussed the slopes of the displacement force curves. This is a wrong statement because this discussion was published first by Bulychev et al. (1975). Thus, there is no reason to state that Sneddon created a new contact theory.
As an example, Galin (1946) applied his general solution to the case of axisymmetric punches whose shape is described by monomial (power-law) functions:
f(r)=Bdrd,
where Bd is the shape constant, [Bd] = L1−d, [·] denotes the physical dimension of a variable, and L denotes the physical dimension of length.
If the shape function is described by Eq. (3.53), then Eqs. (3.46) and (3.47) lead to
P=E1−ν2Bdd2d+12d−1[Γ(d/2)]2Γ(d)ad+1,δ=Bdd2d−2[Γ(d/2)]2Γ(d)ad.
Here d is the degree of the monomial function, and Γ(d) is the Euler gamma function.
From Eq. (3.54), one can obtain the following P–δ relation:
P=E1−ν2[B−1dd22/ddd−1d1d+1[Γ(d/2)]−2d[Γ(d)]1d]δd+1d.
Note Eq. (3.55) was presented by Galin (1946, 1953) (his equations 4.35 and 5.36, respectively) with an omitted minus sign in the exponent of Bd.
It follows from Eq. (3.54) that
P=2dd+1·E1−ν2aδ.
In particular, taking a limit d → ∞ in Eq. (3.54), one obtains the Boussinesq relation (Eq. 3.41) for a flat-ended cylindrical indenter of radius a.
Using the property of the Euler gamma functions Γ(n + 1) = n!, one can show that the Shtaerman (1939) solution is a particular case, d = 2n, of the Galin solution (Eq. 3.55). Here n is a natural number. In particular, one can obtain the Shtaerman (1939) formula (see also equation 5.20 in the book by Johnson, 1985):
P=4nB2nE1−ν2a2n+12·4…2n1·3…2n+1=4nB2nE1−ν2a2n+1(2n)!!(2n+1)!!.
Note that expressions (Eq. 3.54) can be written as
a=(PC(d)K*Bd)1/d+1,δ=(C(d)Bdd+12d)ad,
and the δ–P relation (Eq. 3.55) can be written as
δ=[C(d)Bd(K*)d]1d+1(d+12d)Pd/(d+1),C(d)=d2d+12d−1[Γ(d/2)]2Γ(d).
Taking into account that the shape function for bodies of revolution may be presented in the form of the power series with fractional exponents,
f(r)=∞∑k=1Bdkrdk,dk>0,
and that Hertz-type contact problems with identical contact regions can be superimposed on each other (see, e.g., Galin, 1953; Mossakovskii, 1963), one can obtain the solution for such an indenter as a superposition of solutions to the Hertz-type contact problems having the same fixed contact radius a. Hence, the contact load P and the depth of indentation δ satisfy the following equations (Borodich, 1990a):
P=K*∞∑k=1A(Bdk,dk)adk+1,A(Bdk,dk)=Bdk2dk−1d2kdk+1[Γ(dk/2)]2Γ(dk),δ=∞∑k=1Bdkdk2dk−2[Γ(dk/2)]2Γ(dk)adk.
Note the coefficient 1/2 in Eq. (3.61) was omitted by Borodich (1990a).
In fact, the shape function described in Eq. (3.60) is a generalization of the shape function considered by Jung (1950), Segedin (1957), and Sneddon (1965) when the series are for only integer exponents.
2.4 Solutions to Nonslipping Contact Problems
2.4.1 Historical Preliminaries
Let us consider next the axisymmetric Hertz-type contact problems with nonslipping boundary conditions. If the external parameter of the problem P![]() is gradually increased, then the surface displacements ur(r,0,P)
is gradually increased, then the surface displacements ur(r,0,P)![]() and uz(r,0,P)
and uz(r,0,P)![]() will be functions of both r and the parameter of the problem P
will be functions of both r and the parameter of the problem P![]() . Once the point of the surface contacts with the indenter, its radial displacement does not change further with P
. Once the point of the surface contacts with the indenter, its radial displacement does not change further with P![]() . Hence, instead of the conditions (Eq. 3.13), one can write the nonslipping condition (Eq. 3.14) within the contact region, which in the axisymmetric case can be written as
. Hence, instead of the conditions (Eq. 3.13), one can write the nonslipping condition (Eq. 3.14) within the contact region, which in the axisymmetric case can be written as
∂ur∂P(r,0,P)=0.
Hence, the radial displacements within the contact region do not change with augmentation of the external parameter of the problem. In this formulation, the normal and radial displacements are consistent with the punch shape, and therefore it follows from Eq. (3.12) that g(r) = δ − f(r) and the radial displacements ur(r,0,P)![]() cannot be arbitrary.
cannot be arbitrary.
The analysis of the nonslipping contact problems was performed first incrementally (Goodman, 1962; Mossakovskii, 1954, 1963) for a growth in the contact radius a. Mossakovskii noted self-similarity of the problem for punches described by monomial functions (Eq. 3.53). However, only Spence (1968) pointed out that the solution can be obtained directly without application of the incremental techniques (Gladwell, 1980; Johnson, 1985). Self-similarity of a general 3D frictional Hertz-type contact problem was shown later by Borodich (1993a).
Mossakovskii (1954, 1963) considered only two particular examples of nonslipping contact problems; namely, the problems for a flat-ended cylinder and a parabolic punch. Spence (1968) introduced an alternative method for solution of the problems, corrected some misprints in the Mossakovskii examples, and presented also the solution to the problem for a conical punch.
Following Mossakovskii and Spence, let us take the contact radius a as the external parameter of the problem P![]() .
.
2.4.2 The Mossakovskii Solution for Nonslipping Contact
In 1954 Mossakovskii presented the solution to a mixed boundary value problem for an elastic half-space when the line separating the boundary conditions is a circle. As an example, he gave a solution for a flat-ended circular punch of radius a under the condition of nonslipping contact. In this case, the compressing normal stresses σzz under a flat-ended punch of radius a is
σ0zz(r,0,a)=CMδ01rddrr∫0sin(βlna−xa+x)x√r2−x2dx.
Here δ0 is the depth of indentation of the punch and
β=12πln(3−4ν),CM=8μ(1−ν)π(1−2ν)√3−4ν.
The correctness of formula (Eq. 3.63) was later checked by Keer (1967) and Spence (1968). Speaking about the further calculations of the compressing stress by Mossakovskii, Spence (1968) remarked that a factor of 2 was omitted throughout his paper of 1963, beginning with his equation (2.16). Indeed, Mossakovskii’s papers have various misprints; for example, Mossakovskii’s expression for the contact force for the Mossakovskii–Boussinesq problem obtained by integration of the pressure (Eq. 3.63) over the contact region was not presented in the correct form. The corrected Mossakovskii formula is (Khadem & Keer, 1974; Spence, 1968)
P=4μδ0aln(3−4ν)1−2ν.
However, on this occasion his calculations were correct and Spence’s comment was in error. Formula (3.64) was also presented with a misprint in the book by Johnson (1985) (see his equation 3.105). One can see that the solution differs from the frictionless Boussinesq solution (Eq. 3.41).
Integrating Eq. (3.63) by parts, one obtains the following formula for the pressure under a circular plane punch with unit settlement:
σ0zz(r,0,a)=−2βaCMr∫0χ(x,a)dx√r2−x2(a2−x2),χ(x,a)=cos(βlna−xa+x).
Applying the incremental approach to the solution (Eq. 3.65) with varying radius t of the punch, one can calculate the normal stress under a curved axisymmetric punch:
σzz(r,0,a)=a∫rdδ(t)dtσ0zz(r,0,t)dt.
Developing the Mossakovskii approach, Borodich and Keer (2004b) obtained the following formula for the contact force:
P(a)=16μ(1−ν)ln(3−4ν)π(1−2ν)√3−4νIa∫0dδ(t)dttdt,I=a∫0χ(x,a)√a2−x2dx.
The integral I can be calculated using the Abramov–Muskhelishvili solution to the 2D problem of nonslipping contact between a punch with a straight horizontal base and an elastic half-plane (Borodich & Keer, 2004a):
I=π4√3−4ν1−ν.
Hence, it follows from Eq. (3.67) that the general expression for the force acting on a curved axisymmetric punch at nonslipping contact is
P(a)=4μln(3−4ν)(1−2ν)a∫0dδ(t)dttdt.