1 Introduction

The prevalence of parallel architectures has introduced several challenges from a design-level perspective to an application level [1]. Dealing with these challenges requires new paradigms from circuit design techniques to writing applications for these architectures. Introducing the common application categories [1], which have profound impact on various scientific fields, can be considered as a guide toward the goal of dealing with fundamental problems in parallel environments. Among these applications, sparse matrix-vector multiplication (SpMV) is a fundamental building block for numerous computational hungry applications such as image processing, data mining, structural mechanics, and web page ranking algorithms employed by search engines [2].

Over the past decade, graphics processing units (GPUs) have gained an important place in the field of high-performance computing (HPC) because of their low cost and massive parallel processing powers. A GPU provides tremendous computational power and very high memory bandwidth. It is also very well suited for dense matrix computations; however, several challenges are faced in achieving high performance for sparse matrix computations, which is a well-established class of problems in the parallel computing community [1]. Sparsity patterns vary greatly from one matrix to another, because they can represent random graphs, electronic circuits, social interactions, discretization of partial differential equations (PDEs) on structured or unstructured grids, and a range of other problems. Therefore processing all types of matrices with a fixed format might lead to performance degradation in most cases. On the other hand, architectural parameters greatly impact application performance. For example, improper selection of these parameters adversely affects the performance.

In this chapter, we study the parameterization of the SpMV in order to determine the best data representation to execute on GPUs, depending on properties of different matrices and architectural parameters. Furthermore, we illustrate how auto-tuning can be used to produce efficient implementations across a diverse set of current GPU architectures. In Section 2, we give an overview of the SpMV and different formats, followed by a description of the GPU architecture that used in this study in Section 3. This is followed, in Section 4, by optimization principles for SpMV that have a key effect on the performance of sparse matrix computation. We present our design of an auto-tuner system in Section 5. Finally, we present performance results followed by conclusions in Sections 6 and 7.

2 Sparse matrix-vector multiplication

SpMV is one of the key operations in many scientific computations and is used heavily kernels in various domains of scientific, medical, and engineering studies, including iterative solvers for linear systems of equations, image processing, solving PDEs, and PageRank computation for ranking web pages [2]. SpMV performs the operation $y\leftarrow y+Ax$, where A is a sparse matrix, and x and y are dense vectors. Sparse kernels suffer from memory storage overhead, as well as irregular structure of sparse matrices. Many studies have been on how to optimize and improve the performance of sparse computations on different platforms [3–34]. Because the performance of sparse matrix computations depends on its representation format [3], many researchers proposed various formats to store and represent these matrices [4–16, 32]. For example, Fig. 1 illustrates the performance of SpMV with nd24k input matrix using different formats. As can be seen, the difference among speedups can be up to 45×. Achieving good performance requires selecting proper storage formats by exploiting properties of both the sparse matrix (during runtime) and the underlying machine architecture. However, because there are many different applications with diverse requirements, a unique representation is not suitable for all sparse matrices, as revealed by experimental results [3, 4]. Table 1 shows various matrices used in different applications along with the format that works best for each matrix. This section describes seven state-of-the-art sparse matrix formats. Fig. 2 shows the basic representation formats of sparse matrix.

Table 1

Matrices

Name	Spyplot	DimRow	%NNZ	Avg.	Max.	Description	Best Format
Dense		2000	100	2000	2000	Dense	BCCOO
pdb1HYS		36,417	33	119.3	204	Protein data bank 1HY2S	BELLPACK
consph		83,334	9	72.1	81	Concentric spheres	BELLPACK
cantilever		62,451	10	64.1	78	Cantilever	BELLPACK
pwtk		217,918	2	53.4	180	Pressurized wind tunnel	BELLPACK
rma10		46,835	11	50.6	145	3D CFD of Charleston Harbor	BELLPACK
QCD		49,152	8	39.0	39	Quark propagation	BELLPACK
shipsec1		140,874	2	55.4	102	Ship section	BELLPACK
mac-econ-fwd500		206,500	0.3	6.1	44	Macroeconomics model	HYB
mc2depi		525,825	0.07	3.9	4	2D Markov model of epidemic	ELLPACK
cop20k_A		121,192	2	21.6	81	Accelerator	BCCOO
scircuit		170,998	0.3	5.6	353	Motorola circuit simulation	BCCOO
webbase-1M		1,000,005	0.03	3.1	4700	Web connectivity	HYB
atmosmodd		1,270,432	0.05	6.9	7	CFD problem	DIA
cage14		1,505,785	0.12	18	41	directed weighted graph	ELLPACK
crankseg_2		63,838	35	221	3423	structural problem	CSR(vector)
ldoor		952,203	0.4	48.9	77	structural problem	ELLPACK
nd24k		72,000	55	308	520	ND problem set	BELLPACK
F1		343,791	2	39.5	435	FEM-AUDI engine	CSR (vector)
shallow-water1		81,920	0.4	4	4	CFD problem	ELLPACK

Diagonal format (DIA) uses two arrays to store nonzero elements: DiaVal array stores nonzero values, and DiaOffset records the diameter offsets with respect to the main diameter. The diagonal format is a proper scheme for matrices deriving from the application of stencils to regular grids, a common discretization method because of the nonzero elements in these matrices are distributed in a diametrical way [3]. However, most sparse matrices do not have a diametrical structure, which hinders wide use of this format.

Compressed Sparse Row (CSR) format is probably the most widely used format for storing general sparse matrices [3, 4]. In this format, the input matrix is represented by the following components: CsrVal, which contains nonzero values; ColIdx, which holds the column index of nonzero elements; CsrPtr, which shows the first nonzero element in each row. It includes N + 1 elements, N being the number of rows in the matrix. The number of nonzero elements in row i can be computed from the variance of i and i + 1 arrays in CsrPtr.

CSR (scalar) format assigns one thread to process each row. By doing so, the memory access pattern is not coalescent, which leads to performance degradation. The modified version of the CSR format, CSR (vector), is also proposed in Ref. [4]. In this format one warp is allocated to process each row to achieve the memory access contiguously.

ELLPACK format first shifts the nonzero elements of the matrix to the left then pads each row with zeros, if needed. In order to store a sparse matrix, ELLPACK uses two arrays: EllVal, which stores nonzero elements, and ColIdx, which holds the index of nonzero columns. The ELL format is recommended for vector structures. ELLPACK works well for matrices in which the maximum number of nonzero elements in all rows is not substantially different from the average. However, when the number of nonzeros varies largely between rows, the performance is degraded because of the redundant memory usage and the redundant computation. The ELLPACK format is suitable for matrices with a regular structure.

Coordinate format (COO) is the simplest way to store a sparse matrix. COO keeps a matrix using three arrays: CooVal, RowIdx, and ColIdx, which contain the nonzero data values, the row index of the elements corresponding to CooVal, and the column index of the elements corresponding to CooVal, respectively. All kinds of sparse matrices can be stored in the COO format. In order to implement this format on GPUs, atomic operation is used to collect intrathread results.

Hybrid format (HYB) uses the syntax of COO and ELL representations [4]. In this type, the input matrix is partitioned into two parts based on a parameter, K. The first part of the matrix is stored in the ELLPACK format, and the second part is represented in the COO format. If a row has less than k nonzero elements in the first part, it is padded with zeros. This format is suitable for unstructured sparse matrices.

BELLPACK format [9] compresses the sparse matrix by small dense entry blocks and then reorders the row of blocks according to the number of blocks per row. Finally, in order to reduce the required padding relative to conventional ELLPACK storage, the rows of matrices are partitioned into submatrices, each stored using the ELLPACK scheme. BELLPACK assigns one thread block per block row of the matrix and within a row block; warps are assigned to consecutive register-block rows.

BCCOO format [13] partitions a matrix into a number of subblocks to reduce the size of arrays. The implementation of BCCOO uses three arrays: value contains the nonzero entries and the other two arrays, col_index and BitFlag, contain the corresponding row and column indices for each nonzero element. In order to avoid load imbalance problems, each thread processes the same number of nonzero blocks in a BCCOO scheme.

3 GPU architecture and programming model

GPUs have evolved over the past few years, and increasing demands for HPC across many fields of science make GPUs available for general-purpose computing. GPUs have several thousand threads that operate in groups across large amounts of data in parallel to hide long latency operations.

4 Optimization principles for SpMV

This section describes the principle of performance optimizations based on the architectures and SpMV outlined in pervious sections. In most cases, improperly choosing architectural parameters can significantly affect the performance. However, it is not clear which architectural parameters have the greatest impact on performance. We studied the potential impact of various parameter selections that are appropriate for different representations in order to reach high performance. To understand the behavior of sparse matrix applications in various situations, we studied their performance under different representations and parameters. We identified that the performances of SpMV applications benefit from the effective selection of parameters such as block size, number of registers, and memory hierarchy.

4.1 Block Size

The first parameter that has considerable effect on the performance is block size. Defining the precise number of threads inside a block plays a key role in reaching higher performance. Choosing the value of a block size from high to low can affect the occupancy favorably or adversely, respectively. According to the CUDA architecture, there are hard upper limits on the size of a thread block and active thread blocks on a single multiprocessor in GPUs (i.e., SMs). For example, each SM in Kepler architecture can have 2048 simultaneously active threads, or 64 warps. These may come from 2 thread blocks of 32 warps with 100% occupancy or 2 thread blocks of 24 warps with 75% occupancy. In addition to the previously mentioned limitations, the number of active blocks in an SM depends on other resource limitations, such as register file and shared memory. To illustrate the importance of choosing parameter values for sparse matrix representations, the results of experiments with different parameter selections are shown in Fig. 3. This figure shows the speedup due to block size on the DIA format when using various block sizes with the atmosmodd matrix.

Regarding the performance of the DIA format in Fig. 3, we can see that the number of threads inside a block is crucial to the performance of SpMV on a GPU 512 resident threads per block deliver an average of 2× speedup over the 64-thread scenario. It is because the number of resident threads per SM (64 × 16, 1024 threads, 50% occupancy, in contrast to 514 × 4, 2048 threads, 100% occupancy in Tesla K20X and 648, 512 threads, 33% occupancy, in contrast to 51 × 23, 15 × 36 threads, 100% occupancy in GTX480) heavily influence the performance of DIA format.

4.2 Register

The number of allocated registers for each thread is another factor that affects the performance. Occupancy rate depends on the amount of register memory each thread requires. Increasing the register usage may consequently decrease the SM’s occupancy and utilization. Register memory access is very fast, but the number of available registers per block are limited. For example, the maximum and minimum hardware limits for compute capability 3.x are 255 and 16 registers per thread, respectively. The limit of registers per thread are specified by the -maxrregcount flag at compile time to increase the number of concurrently running threads and to improve thread-level parallelism in running kernels on GPUs. Some kernels use less than 16 registers in the single-precision mode, such as DIA. Reducing the register usage can lead to higher performance. However, it may cause spilling registers into L2 cache. Spilling occurs if the register count is exceeded, which in turn leads to an increase in reading/writing from/to L2 cache, which is expensive. Experiments are used to determine the optimum balance of spilling versus occupancy. As shown in Fig. 4, varying the number of registers assigned to each thread has changed the performance of the COO format for the pdb1HYS input matrix. The optimized kernels use enough extra registers to maintain the utilization of SMs, which combined with more efficient memory accesses, results in a speedup of 1.33× compared to the initial kernel configuration. Table 3 shows the best register configuration achieved for each format.

4.3 Memory

Most highly multithreaded applications such as SpMV are memory-bounded, and their performance depends strongly on efficient use of the memory subsystem. Therefore information about the interaction of SpMV applications with the memory system is crucial for tuning the performance. The capability to configure the shared memory and L1 cache provides opportunities to select appropriate configurations for a given representation or an input matrix. The patterns of the global memory accesses govern the amount of local memory needed to allocate as L1 cache. For example, in applications with regular memory access patterns, increasing the size of the shared memory can improve the performance; however, in cases with more frequent or unpredictable accesses to larger regions of DRAM, L1 cache size has a strong impact on the performance [38]. In addition to L1 cache and shared memory, the read-only texture memory can also be utilized. It provides more effective bandwidth by reducing memory traffic and increases the performance compared to accessing the global memory. For example, The vector x can be kept in the texture memory, which improves performance through improving the utilization of memory bandwidth in GPUs [4, 35, 36]. The impact of different configurations of memory on bandwidth are illustrated in Fig. 5. For this case, the ELLPACK kernel is launched for nd24k matrix. The memory configuration of GTX 480 also contains additional options in which the L1 cache has been disabled in order to analyze how the performance is changed. As shown in this figure, the achieved bandwidth for nd24k matrix increases when the L1 cache size grows. We further improve kernels by storing the vector x in the texture memory to enhance the cache hit rates when accessing the vector. In addition, the elements of this vector are reused during the execution, and the locality of accesses to a location is high, which results in performance improvement.

5 Platform (Adaptive Runtime System)

In this section, we discuss the details of an adaptive runtime system, which is proposed to automatically choose the optimum storage scheme for an input sparse matrix. We consider both GPU architectural parameters and characteristics of sparse matrices to optimize the SpMV performance and to select the best format. To that end, after determining which parameters to vary and evaluating the amount of those values, all kernels were configured with these final values. Our auto-tuner consists of two phases, namely a training phase and a processing phase. In the training phase, the auto-tuner chooses a subsample from an input sparse matrix and converts it to all basic representations. In the processing phase, we assess the performance of each format to identify the best one. A flowchart of this process is shown in Ref. [39]. It should be mentioned that we used basic formats that are frequently used for storing sparse matrices and some other formats that are derived from them, such as HYB [4]. Furthermore, there is a possibility to consider new formats in our auto-tuner. For example, we added HYB, BELLPACK [9], and BCCOO formats [13] to our auto-tuner.

The training phase involves the generation of samples from matrices. It should be noted that completely running SpMV applications using each representation format is a tremendously time-consuming process. For this reason, our auto-tuner uses a small portion of the input matrix to test the performance of all schemes. To ensure that the chosen submatrix is the appropriate metric to find the best format, we divide an input matrix into five submatrices, and all kernels execute 10% of each submatrix to choose the suitable storage scheme for an input submatrix. In most matrices, the best format for all submatrices has the same storage format. It must be noted that there is a discrepancy between some submatrices of the matrix that chose the ELLPACK or HYB format as the best format. The submatrices with a small standard deviation value selected the ELLPACK format, and the submatrices with a disparity between MaxNNZ and AvgNNZ in their structure, chose the HYB storage scheme. This mismatch can be ignored because there is no notable difference between these submatrices from a performance point of view. Therefore, in this system, we use the first portion of matrices in an initial stage. The auto-tuner configures the kernels of formats by using the information that is extracted from the parameter extraction stage. This approach allows us to evaluate sparse matrices while preserving the execution time across changing formats.

The processing phase executes the input application for five iterations with different representation formats. The first five iterations help to ensure stability in an application’s behavior and are adequate for predicting the appropriate representation format. The auto-tuner framework inspects the behavior of applications by collecting a number of performance metrics such as computing power and bandwidth. It is worth mentioning that the results of this phase depend on the input matrix characteristics, such as distribution of nonzero elements. According to the results of the previous stage, the auto-tuner picks the storage format that yields the best performance to run the rest of the application. One of the outstanding features of our runtime system is its scalability through which users can add new storage formats to the proposed system. Furthermore, the auto-tuner is portable and can be extended to different GPU architectures (e.g., Maxwell).

6 Results and analysis

In this section, we present and analyze the performance and bandwidth of SpMV for each of the two architectures. Because the elements of matrices are floating-point numbers and all benchmarks are run on the same ISA, GFlop/s is a proper metric to measure and compare the performance. It is worth mentioning that these metrics were widely used in previous studies. In addition, in all kernels, we assume that matrices and vectors reside in the GPU’s device memory, eliminating the need for any PCIe transfers. This is a reasonable assumption for any local iterative sparse solver.

6.1 Parameters Setting Experiments

Block size

We searched the block size space through different configurations for the optimal value of the number of threads inside a block. The same experiment was conducted when using all formats. The total size of a block was limited to 2048 and 1536 threads in GK110 and Fermi architectures, respectively. Fig. 6 shows the performance of the basic format for different input matrices. As shown in this figure, the optimal value for the COO format is 128 threads per block. The best block size for CSR (scalar) format is 64 threads. In this format, a thread processes each row, and each row has a different number of nonzero elements, which causes some threads to make extra calculations, while others will stay idle. Therefore a simple thread-per-row decomposition strategy when matrices have different NNZ per rows is a challenge for parallelism in GPUs. The BCCOO format has shown the best performance when using 256 threads per block. Moreover, CUDA provides a barrier synchronization mechanism for the threads in the same block. Therefore, by increasing the size of a block, more active threads can cooperate [35]. On the other hand, there is no native way to synchronize all threads from all blocks, and the synchronization overhead leads to a reduction in performance. That is why, 512 threads per block yield the best performance for ELLPACK, BELLPACK, CSR (vector), and DIA formats. These formats benefit from more active threads with a minimum number of blocks. Using smaller blocks reduces their performance because of the significant interblock synchronization overhead. The best configurations achieved in this stage will be used when running the applications in our adaptive environment.

Register

The primary limitation is the maximum number of threads on SMs, primarily imposed by the number of 32-bit registers that can be allocated across all the threads inside an SM. The register limit constrains the number of active blocks and the amount of parallelism among threads because only 65,536 (32,768 for compute capability 2.x) registers are available for each SM, and the maximum number of registers that can be accessed by a thread are 255 in the GK110 architecture and 64 in the Fermi architecture. Considering the restrictions on the number of registers, the measure of occupancy of CSR (vector) on GTX480 is shown in Table 4. During compilation, the NVCC compiler allocates 27 and 33 registers to each thread of the CSR (vector) kernel for single- and double-precision computations, respectively. It should be noted that

Table 4

The Rate of Occupancy of CSR (Vector) Based on the Number of Allocated Registers to Each Thread on GTX480

Number of Registers	20	25	30	35
Occupancy for single-precision (%)	100	66	66	66
Occupancy for double-precision (%)	100	66	66	33

double-precision operations require more registers. However, all allocated registers are rarely used, and a poor choice will lead to a poor performance. Therefore reducing the number of registers can dramatically improve the performance for some matrices by increasing the number of standby registers, and consequently more active threads will be accessible inside a block. To illustrate the effect of the register file, Fig. 7 shows the performance of SpMV using basic formats. Reducing the number of registers delivers better performance except for ndk24 and crankseg_2 input matrices. Threads need more registers to compute rows of these matrices because of their structure and distribution of nonzero elements. Moreover, other matrices do not require many registers, and register spilling does not degraded the performance significantly.

Memory

Memory optimization is a key factor in improving the performance of memory-bound irregular applications such as SpMV. In this section, we evaluated all possible configurations of L1 cache size and set associativity to investigate the cache size effects on SpMV performance. Figs. 8 and 9 present the results, and as can be seen, the memory access patterns of sparse matrices govern the performance of these types of applications. To compare the performance based on the cache size, we conclude that a small L1 cache size generates huge cache capacity misses. Touching a small fraction of a large block of data implies that a large fraction is not accessed. Therefore buffering a large amount of data into the shared memory of GPUs suffers from high miss rates and increases the data transfer time by performing many address calculations and memory operations. On the other hand, using a data cache that brings only a cache line (i.e., 128B) is more beneficial because the L1 cache latency is much lower than shared memory latency. Results show that increasing cache size leads to the overall performance improvement in sparse matrix operations. Furthermore, we exploit the read-only texture memory for the multiplied vector x to improve the cache hit rate for accessing its elements. For example, cache hit rates for cantilever and atmosmoddmatrices are equal to 99% (calculated by Nvidia Visual profiler [40]). We observe a better performance, and the access pattern of matrices is a good match for the texture cache. In addition, because of the regular accesses to the Dense matrix, there is no performance improvement.

6.2 Adaptive Runtime System

We present and analyze the results of our auto-tuner on each of the two architectures. The last group of bars represents the achieved average performance. Having selected the best parameters for each representation in the previous sections, we measured the performance of our system when using these parameters to run the entire application. The last bar of each matrix shows the performance of the adaptive system. Our framework takes advantage of optimized SpMV implementations and obtains the maximum speed up of 2.1 × (single-precision) and 1.6× (double-precision), as well as determining the optimal formats as shown in Figs. 10 and 11. We discuss only the results of GTX480 in this section; refer to the original reference studies for additional details [39].

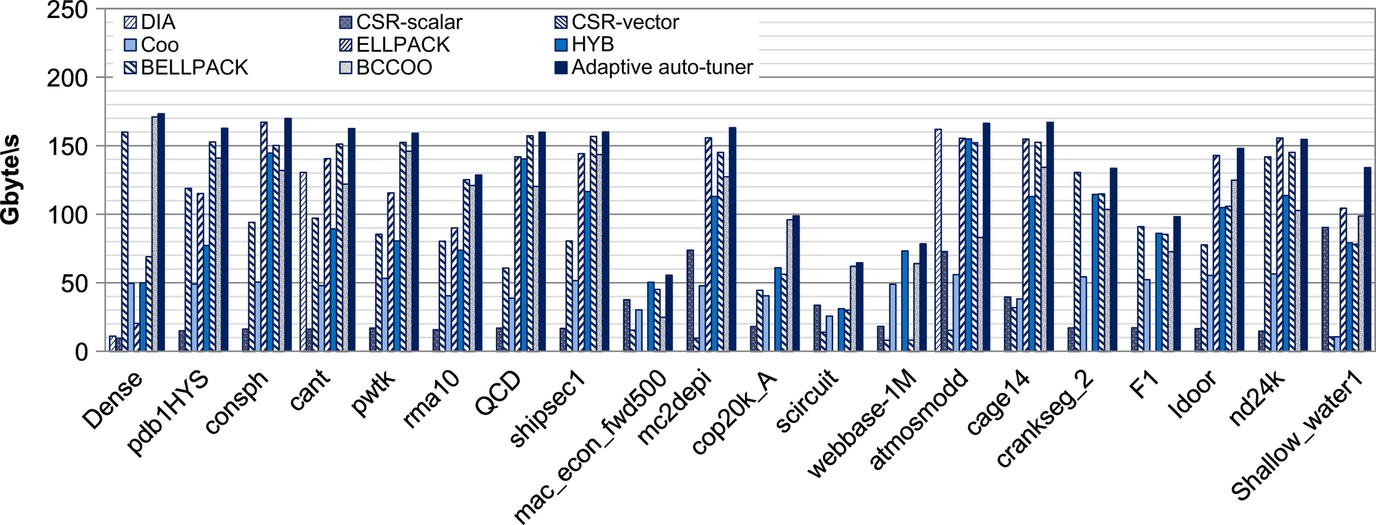
In order to evaluate the accuracy of our system, we conducted several experiments with different matrices. Figs. 10 and 11 show the performance of SpMV computation for various sparse matrices on GTX 480. The atmosmodd matrix has a strictly diagonal structure and a symmetric nonzero pattern. The data reuse is improved by a contiguous access pattern of rows to vector x. As a result of these properties, the DIA format is well suited for this matrix. CSR (vector) delivers better performance for F1 and crankseg-2 matrices, which have more than 32 nonzero entries per row. These matrices could not have a satisfactory performance using the ELL format or extended version of this format because of the great difference between MaxNNZ and AvgNNZ. When applied to matrices with large standard deviation values, the vectorized CSR kernel achieves better performance. The ELLPACK implementation exhibits the best performance for cage14, ldoor, mc2depi, and shallw water1 matrices with respect to the number of rows and the distribution of nonzero entries per row. The difference between MaxNNZ and AvgNNZ in matrices mc2depi and Shallow water1 is zero, which leads to negligible padding and lower memory overhead. The overall size of the portion of memory required is reduced because of the lower amount of padding. In addition, it helps loading more useful data in the cache and improves data reuse in the cache. Although the BELLPACK format is also proper for cage14 and ldoor, it takes too much time to convert them to this format; for example, cage14 takes 7474.02 s to convert to BELLPACK format.

Matrices such as mac_econ_fwd500 and webbase-1M with less than five nonzero entries per row could not benefit from CSR (vector) because several threads will be idle when a row is much shorter than the warp. Moreover, the great difference between MaxNNZ and AvgNNz values result in the ELL implementation that is not suitable for these matrices. The hybrid format achieves good performance for these kinds of sparsity patterns and solves the problem with the robustness of COO. However, the performance of the HYB format would be low for small matrices because of the overhead introduced by requiring three different kernels to compute SpMV. Indeed, the performance of block-based formats is determined by input matrices whose structure is a block structure (i.e., Dense matrix). Matrices from scientific problems whose structures contain mixed block structures such as cop20K_A and Scircuit reach the best performance by the BCCOO format. The performance of BCCOO is reduced substantially as a result of using matrices that are derived from the graph. It should be mentioned that the BCCOO format supports only single-precision floating-point formats [34] and suffers from the significant overhead associated with generating the data structure. BELLPACK works best for other matrices with a small dense block substructure. In addition, padding matrices with explicit zeroes result in a considerable memory overhead and performance degradation in unstructured matrices.

We compare the results of the proposed auto-tuner and the methods introduced by Bell and Garland [4] and Neelima et al. [19] (see Zardoshti [39] for more information). By comparison, we see some mismatches in results that are derived for two reasons. First, we use a wider range of formats in our auto-tuner, which leads to expanding the search space of the auto-tuner and improves the overall performance of SpMV. On the other hand, the method of Neelima et al. [19] just analyzes the basic formats in their static model, and it is difficult to extend the model to include new formats. Consequently, predicting a suitable format based on the structure of a matrix may not always be accurate, especially for sparsity patterns. More precisely, the static model shows that the COO implementation delivers the best performance for mac_econ_fwd500, while the HYB format provides better performance.

7 Summary

We presented a novel solution to select the best storage format for SpMV, which is easy to state and to analyze. The diversity of architectural designs and input matrix characteristics means that a complex combination of architecture- and matrix-specific techniques are essential to achieve this level of performance. We designed and implemented an adaptive GPU-based SpMV system. First, we thoroughly analyzed the factors that impact the performance of SpMV algorithms using basic sparse matrix representation formats. All optimized implementations delivered substantially better performance. Second, based on these experiments, we proposed an adaptive runtime system that adapts to the behavior of the running application by profiling a small portion of the input matrix. Experimental results revealed that the proposed runtime system adapts well to the behavior of different applications by selecting the appropriate representation for each input sparse matrix. The preliminary results exhibited that the runtime system improves the performance of SpMV by 2.1× for single-precision and 1.6× for double-precision formats, on average.