Hour 6
Linear Equations: Solving More Complex Equations
Now that you can solve simple equations that have just one operation, the next goal is to learn how to solve more complex equations. These new equations contain two or more of the basic operations (addition, subtraction, multiplication, and division). You solve them using more than one of the previous hour’s four properties of equality in a logical order. The challenge comes in knowing which property to use and when to use it. Before the end of this hour, you will be able to rearrange any linear equation’s terms to isolate the variable—in other words, to solve the equation.
Solving Equations with Combined Operations
How can you decide which is the better deal for a two-day trip if one car-rental company charges $33 per day with unlimited miles and another charges $20 per day and 10¢ per mile? The answer depends on how many miles you plan to drive, and knowing the break-even point will help you make your decision. This real-life problem is an excellent example of using algebra to find a useful answer, and you will be able to solve this and similar problems at the end of this hour.
Take a moment to review an equation from Hour 5:
Solve x - 9 = -1.
To isolate the variable, add 9 to both sides of the equation and then simplify the expressions:
x - 9 + 9 = -1 + 9
x + 0 = 8
x = 8
x + 0 = 8
x = 8
To check, put 8 in for x in the original equation: 8 - 9 = -1 is true. Therefore, x = 8 is the solution.
In the previous example, only one operation (subtraction) is involved, and you simply apply the addition property of equality to isolate the variable. Now consider a more complex equation that has two operations:
2x + 3 = 9
GO TO ◀
The properties of equality for +, -, ·, and ÷ help you move terms from one side of an equation to the other when used in the right order. See Hour 4 for a full set of examples of these properties.
Isolating the variable requires moving the 2 and also moving the 3. Which should you do first? Let’s try moving the 3 by subtracting 3 from both sides of the equation:
2x + 3 = 9
2x + 3 - 3 = 9 - 3
2x + 0 = 6
2x = 6
2x + 3 - 3 = 9 - 3
2x + 0 = 6
2x = 6
Can you now move the 2? Yes, the division property of equality lets you divide both sides by 2. To finish solving the equation:
2x = 6
2x ÷ 2 = 6 ÷ 2
x = 3
2x ÷ 2 = 6 ÷ 2
x = 3
To check, put 3 in for x in the original equation: 2 · 3 + 3 = 9 → 6 + 3 = 9 → 9 = 9, which is true. Therefore, x = 3 is the solution. Look once again at the original equation:
2x + 3 = 9
Instead of subtracting 3 from both sides of the equation, what would have happened if you had tried to move the 2 first? Moving the 2 requires dividing both sides of the equation by 2. But isn’t the 3 in your way? So dividing both sides by 2 is not going to work here. By moving the 3 first, you get an equation 2x = 6 that can easily be solved when you divide both sides by 2.
Solving 2x + 3 = 9 is a perfect example of the power of the properties of algebra. Being able to solve this type of equation builds up your math skills, taking you beyond the simple arithmetic operations. You are faced with choosing between two equally useful properties (subtraction and division) and then applying them in the correct order to find the solution.
PROCEED WITH CAUTION
Many of the simpler equations in Hour 5 could easily be solved mentally. 2x + 3 = 9 has just enough complexity that you don’t see the solution right away. Yet by applying two properties of equality, you can solve it quite easily. Showing the solution steps helps you avoid careless errors.
This higher-level algebra process gives you a new perspective that allows you to solve problems that can’t be solved using basic arithmetic. At the end of this hour, you will see real-life situations that can be written as algebraic equations and solved. The solutions to these more complex equations are used extensively in research, finance, business, and medicine. Before you learn how to write equations for various situations, learn from the following examples how to solve equations that contain more than one operation.
Consider the following equation: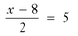
It has two operations (subtraction and division), so its solution needs at least two steps. Should you first add 8 to both sides or multiply both sides by 2?
Adding 8 to the fraction  will not make the -8 become a 0, so try multiplying both sides by 2. The steps look like this:
will not make the -8 become a 0, so try multiplying both sides by 2. The steps look like this: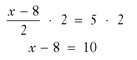
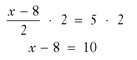
Now adding 8 to both sides gives the solution x = 18.
GO TO ◀
Use the Sign Rules from Hour 3 for adding positive and negative numbers when combining like terms.
To check, put 18 in for x in the original equation: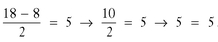 . Therefore, x = 18 is the solution.
. Therefore, x = 18 is the solution.
Some equations have like terms that need to be combined before they can be solved, as in this sample equation: 3x + 2x - 8 = 3 + 9
The 3x and 2x are like terms, and 3 and 9 are also like terms. Combine them, and the equation becomes this:
5x - 8 = 12
Solve it using the addition and division properties of equality, deciding which to do first. Dividing both sides by 5 won’t work because the left side is 5x - 8. You need to first move the 8 by adding 8 to both sides. The steps are as follows:
5x - 8 = 12
5x - 8 + 8 = 12 + 8
5x = 20
5x ÷ 5 = 20 ÷ 5
x = 4
5x - 8 + 8 = 12 + 8
5x = 20
5x ÷ 5 = 20 ÷ 5
x = 4
To check, put 4 in for x, being careful to use the original equation:
3 · 4 + 2 · 4 - 8 = 3 + 9 → 12 + 8 - 8 = 12 → 20 - 8 = 12 → 12 = 12.
Therefore, x = 4 is the solution.
Therefore, x = 4 is the solution.
The following example includes combining like terms and working with negative numbers, but you still use the four properties of equality to get the solution:
Solve -4a + 3 - 2a + 10 = -5.
Combine the like terms and use the division and subtraction properties to solve it:
-4a + 3 - 2a + 10 = -5
-6a + 13 = -5
-6a + 13 - 13 = -5 - 13
-6a = -18
-6a ÷ -6 = -18 ÷ -6
a = 3
-6a + 13 = -5
-6a + 13 - 13 = -5 - 13
-6a = -18
-6a ÷ -6 = -18 ÷ -6
a = 3
To check, put 3 in for a in the original equation: -4 · 3 + 3 - 2 · 3 + 10 = -5 → -12 + 3 - 6 + 10 = -5 → -9 + -6 + 10 = -5 → -15 + 10 = -5 → -5 = -5. Therefore, a = 3 is the solution.
Now try solving these equations, checking your answers on page 69.
1. 5x - 4 = 11
2. -3a - 6 = 9
3. 10 + 4c - 5 + 2c = -7
4. 
The car rental problem can be solved using an equation like those you just did, but it is better to wait and do all the word problems at the end of the hour—there are more types of equations to learn about first.
Solving Equations with the Variable on Both Sides
One company offers you an annual salary of $18,000 plus a $1,500 raise each year, and another offers an annual salary of $20,000 and a $1,000 raise each year. Assuming both jobs are equally appealing to you in all other ways, which of these two pay scales should you choose? The answer depends on how many years you work there. This problem is written as an equation with a variable on both sides of the equals sign, and it has a slightly different solution process. You will see this process shown in some sample equations as you work toward solving it and other word problems the end of the hour.
Follow the steps to solve for x in the next example:
7x = 4x + 15
Your goal, as always, is to isolate the variable. With an x on both sides of the equals sign, which variable will you isolate? The answer is that isolating the variable has to wait because the two x terms must first be combined. The equals sign separates the 7x from the 4x, so your first job is moving either the 7x or the 4x to the other side of the equals sign.
JUST A MINUTE
Remember that the properties of equality allow you to move numbers from one side to the other until you have isolated the variable. These same properties make it possible to move terms with variables, too.
Look again at the equation you are trying to solve:
7x = 4x + 15
The subtraction property of equality lets you subtract either 7x or 4x from both sides of the equation. Try subtracting 4x from both sides and see the result:
7x - 4x = 4x + 15 - 4x
3x = 15
3x = 15
Dividing both sides of the equation by 3 isolates the variable, and you have the solution:
3x ÷ 3 = 15 ÷ 3
x = 5
x = 5
To check, put 5 in for x in the original equation:
7 · 5 = 4 · 5 + 15 → 35 = 20 + 15 → 35 = 35
Therefore, x = 5 is the solution.
You did have two choices in solving this equation: you could have subtracted 7x or 4x from both sides in the first step. See what would have happened if you had subtracted 7x from both sides of the original equation:
7x - 7x = 4x + 15 - 7x
0 = -3x + 15
0 - 15 = -3x + 15 - 15
-15 = -3x
-15 ÷ -3 = -3x ÷ -3
5 = x or x = 5
0 = -3x + 15
0 - 15 = -3x + 15 - 15
-15 = -3x
-15 ÷ -3 = -3x ÷ -3
5 = x or x = 5
The solution is still x = 5, but it took many more steps to find the solution. In general, moving the variable term with the smaller coefficient requires fewer solution steps.
STRICTLY DEFINED
Remember that a coefficient is the number directly in front of a variable and is multiplied by the variable. For example, the coefficient of 7x is 7 and the coefficient of -3a is -3.
Another type of equation includes parentheses that are affected by the distributive property. Some simplifying steps are needed before you can move any of the terms from one side to the other.
Follow these steps that show how to find the next equation’s solution:
6(x - 2) + x = 2(x + 5) + 3
6x - 12 + x = 2x + 10 + 3
7x - 12 = 2x + 13
7x - 12 - 2x = 2x + 13 - 2x
5x - 12 = 13
5x - 12 + 12 = 13 + 12
5x = 25
5x ÷ 5 = 25 ÷ 5
x = 5
6x - 12 + x = 2x + 10 + 3
7x - 12 = 2x + 13
7x - 12 - 2x = 2x + 13 - 2x
5x - 12 = 13
5x - 12 + 12 = 13 + 12
5x = 25
5x ÷ 5 = 25 ÷ 5
x = 5
To check, put x = 5 in for x in the original equation:
6(5 - 2) + 5 = 2(5 + 5) + 3 → 6 · 3 + 5 = 2 · 10 + 3 → 18 + 5 = 20 + 3 → 23 = 23.
Therefore, x = 5 is the solution.
JUST A MINUTE

From Hour 4: The Distributive Property
Multiplying a sum by a number is the same as adding the product of the numbers. a · (b + c) = (a · b) + (a · c)
Now try solving these equations, checking your answers on pages 69-70.
5. 12x + 3 = 10x + 7
6. 6 - 2x = 3x - 9
7. -6x + 8 = 2x
8. 4(a - 5) = -24
There’s just one more detour before you learn how to write the equation and find the answer to the rental car and salary questions.
In all the equations you have solved so far, each solution was an integer and each equation had only one solution. To make it easier for you to learn the algebraic processes for solving equations, the problems have been chosen so that each solution is an integer. However, solutions can be any real number, which you recall includes rational and irrational numbers. Fractions and decimal solutions are certainly possible and are common in real-life situations.
Solving Equations with No Solutions or Many Solutions
Take a moment to consider two questions. Does every equation have a solution? Can there be more than one solution to an equation?
See what happens as you follow the steps in the next equation:
8x = 2(4x + 3)
8x = 8x + 6
8x - 8x = 8x + 6 - 8x
0 = 6
8x = 8x + 6
8x - 8x = 8x + 6 - 8x
0 = 6
It is not possible for 0 to equal 6, so something must have gone wrong in solving this equation. But as you carefully follow each of the steps in the solution, you see that each step is the result of an algebraic property, and everything is done correctly.
So how can there be a solution of 0 = 6? The original equation looked perfectly fine, and the steps were going along in order, but the x terms disappeared as the process moved from the third to the fourth step. Whenever this occurs, the equation is said to have “no solution,” and that is the answer that should be given for this equation. There is no numerical value that can be substituted in place of x to make this equation a true statement. The equation has no solution.
PROCEED WITH CAUTION
It is possible for an equation to have no solution or to have an infinite number of solutions—all real numbers!
Now follow the steps in another sample equation:
3x + 2 = 2(x - 5) + x + 12
3x + 2 = 2x - 10 + x + 12
3x + 2 = 3x + 2
3x + 2 - 3x = 3x + 2 - 3x
2 = 2
3x + 2 = 2x - 10 + x + 12
3x + 2 = 3x + 2
3x + 2 - 3x = 3x + 2 - 3x
2 = 2
Solving the previous equation causes the x terms to disappear, just as they did in the earlier example. But this time the steps end with a true statement of 2 = 2. When this happens, the solution is “all the real numbers” because 2 does equal 2. No matter what number you use for x in the original equation, the steps will always lead you to a number equaling itself. The solution to this type of equation is all the real numbers.
Seldom will an equation’s solution be “all the real numbers” or “no solution,” but you need to be prepared when it happens.
Now try solving these equations, checking your answers on page 70.
9. 6b + 8 = 2(3b + 5)
10. 6b - 24 = 3(2b - 8)
Solving Practical Problems Using Linear Equations
GO TO ◀
Refer to Hour 1 for the table of word phrases and their algebra operations.
Now it’s time to put your equation-solving skills to work in real-life situations like the rental car and salary offer problems. As in Hour 1, the first task is to write the algebraic equation based on the given information.
Let’s begin with the rental car problem from earlier this hour. How can you decide which is the better deal for a two-day trip when one car-rental company charges $33 per day with unlimited miles and another charges $20 per day and 10¢ per mile? This question is easily answered by writing and solving an equation. First decide what the variable is in this situation. The number of days doesn’t vary; it’s 2. But the number of miles you will drive can change, so m for miles is the variable for the equation.
By finding out how many miles will make the two companies’ costs the same (equal), you’ll be able to choose the better deal based on the number of miles you plan to drive. As you write the equation, begin with the first company, which charges $33 for each of the two days. You want to know when that equals the other company’s rate, which is $20 for each of the two days plus 10¢ per mile.
Here’s the information in equation form, followed by the steps to find the solution. You may want to use a calculator for the larger numbers and decimals that often appear in real-life word problems.
33 · 2 = 20 · 2 + .10 · m
66 = 40 + .10 · m
66 - 40 = 40 + .10 · m - 40
26 = .10 · m
26 ÷ .10 = .10 · m ÷ .10
260 = m
66 = 40 + .10 · m
66 - 40 = 40 + .10 · m - 40
26 = .10 · m
26 ÷ .10 = .10 · m ÷ .10
260 = m
To check, put 260 into the original equation:
33 · 2 = 20 · 2 + .10 · 260
66 = 40 + 26
66 = 66
66 = 40 + 26
66 = 66
Therefore, 260 miles is the break-even point, where the cost for your trip will be the same at both companies. Since the first company allows you to drive unlimited miles, it’s the better deal if you plan to go over 260 miles. If your trip is less than 260 miles, the second deal will save you some money. Of course, taxes are going to be added to the cost, but at least you have the number of 260 miles to help make your final decision, all thanks to algebra!
Look again at the salary question. One company offers you an annual salary of $18,000 plus a $1,500 raise each year, and another company offers an annual salary of $20,000 and a $1,000 raise each year. Assuming both jobs are equally appealing to you in all other ways, which of these two pay scales should you choose? The answer depends on how many years you plan to work at the company. Knowing how many years it takes for the salaries to equal each other will help you make the decision. The number of years is the variable here, so use y for years.
The first company’s offer is $18,000 plus $1,500 times y for each year that goes by. The second offer is $20,000 plus $1,000 times y for each year that passes. Write these as algebraic expressions and see when they are equal:
18,000 + 1,500 · y = 20,000 + 1,000 · y
18,000 + 1,500 · y - 1,000 · y = 20,000 + 1,000 · y - 1,000 · y
18,000 + 500 · y = 20,000
18,000 + 500 · y - 18,000 = 20,000 - 18,000
500 · y = 2,000
500 · y ÷ 500 = 2,000 ÷ 500
y = 4
18,000 + 1,500 · y - 1,000 · y = 20,000 + 1,000 · y - 1,000 · y
18,000 + 500 · y = 20,000
18,000 + 500 · y - 18,000 = 20,000 - 18,000
500 · y = 2,000
500 · y ÷ 500 = 2,000 ÷ 500
y = 4
To check, put 4 in for y in the original equation:
18,000 + 1,500 · 4 = 20,000 + 1,000 · 4
18,000 + 6,000 = 20,000 + 4,000
24,000 = 24,000
18,000 + 6,000 = 20,000 + 4,000
24,000 = 24,000
In four years, the $18,000 annual salary with $1,500 raises each year will equal the pay you will get at the other company. After four years, you will be earning more at the company that offered you only $18,000 to start. Setting up and solving the equation allows you to make the comparison and gives you the number of years it takes for the salaries to be the same. The final decision is still up to you.
Now try writing and solving these equations, checking your answers on page 70.
11. Sue has $125 in her daughter’s piggy bank. How long will it take for her to have $200 if she adds $7.50 each week?
12. Find a number whose product with 8 is the same as its sum with 35.
13. Five times a number, increased by 12, is the same as twice the number increased by 36. Find the number.
Answers to Sample Problems in Hour 6
1. 5x - 4 = 11 → 5x - 4 + 4 = 11 + 4 → 5x = 15 → 5x ÷ 5 = 15 ÷ 5 → x = 3
2. -3a - 6 = 9 → -3a - 6 + 6 = 9 + 6 → -3a = 15 → -3a ÷ -3 = 15 ÷ -3 → a = -5
3. 10 + 4c - 5 + 2c = -7 → 5 + 6c = -7 → 5 + 6c - 5 = -7 - 5 → 6c = -12 → 6c ÷ 6 = -12 ÷ 6 → c = -2
4. 

5. 12x + 3 = 10x + 7 → 12x + 3 - 10x = 10x + 7 - 10x → 2x + 3 = 7 → 2x + 3 - 3 = 7 - 3 → 2x = 4 → 2x ÷ 2 = 4 ÷ 2 → x = 2
6. 6 - 2x = 3x - 9 → 6 - 2x + 2x = 3x - 9 + 2x → 6 = 5x - 9 → 6 + 9 = 5x - 9 + 9 → 15 = 5x → 3 = x or x = 3
7. -6x + 8 = 2x → -6x + 8 + 6x = 2x + 6x → 8 = 8x → 8 ÷ 8 = 8x ÷ 8 → 1 = x or x = 1
8. 4(a - 5) = -24 → 4a - 20 = -24 → 4a - 20 + 20 = -24 + 20 → 4a = -4 → 4a ÷ 4 = -4 ÷ 4 → a = -1
9. 6b + 8 = 2(3b + 5) → 6b + 8 = 6b + 10 → 6b + 8 - 6b = 6b + 10 - 6b → 8 = 10. 8 can never equal 10, so this equation has no solution.
10. 6b - 24 = 3(2b - 8) → 6b - 24 = 6b - 24 → 6b - 24 - 6b = 6b - 24 - 6b → -24 = -24. -24 always equals -24, so this equation’s solution is all the real numbers.
11. Let w = number of weeks. The equation is 125 + 7.50 · w = 200 → 125 + 7.50 · w - 125 = 200 - 125 → 7.50 · w = 75 → 7.50 · w ÷ 7.50 = 75 ÷ 7.50 → w = 10. It will take 10 weeks.
12. Let x = the number. The equation is 8x = x + 35 → 8x - x = x + 35 - x → 7x = 35 → 7x ÷ 7 = 35 ÷ 7 → x = 5
13. Let x = the number. The equation is 5x + 12 = 2x + 36 → 5x + 12 - 2x = 2x + 36 - 2x → 3x + 12 = 36 → 3x + 12 - 12 = 36 - 12 → 3x = 24 → 3x ÷ 3 = 24 ÷ 3 → x = 8
Review
Hour’s Up!
Based on what you’ve learned in Hour 6, solve the following equations. Check your answers with the solution key in Appendix B.
1. 6x + 3 = 15
a. x = 3
b. x = 4
c. x = 1
d. x = 2
2. -5a - 12 = 3
a. a = 2
b. a = -3
c. a = 3
d. a = -2
3. 3x + 7x = 40
a. x = 2
b. x = 1
c. x = 4
d. x = 3
4. 6 + 5x - 8 + 2x = 19
a. x = 3
b. x = -3
c. x = 2
d. x = -2
5. 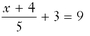
a. x = 2
b. x = 26
c. x = -4
d. x = 1
6. 6b + 7 = 4b + 9
a. b = 1
b. b = 2
c. b = 3
d. b = 4
7. 4 - 3x = 5x - 12
a. x = -2
b. x = 2
c. x = 1
d. x = -1
8. -3 (a + 2) = 2a + 4
a. a = -2
b. a = 2
c. a = 1
d. a = -1
9. One car-rental company charges $42 per day with unlimited mileage. Another company charges $30 per day plus 15¢ per mile. You need to rent a car for a three-day trip. Find the break-even point, where the cost is the same for the two companies.
a. 120 miles
b. 200 miles
c. 240 miles
d. 300 miles
10. Six times a number, increased by 20, is four less than eight times the number. Find the number.
a. 3
b. -4
c. -3
d. 12
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.
