Hour 20
Solving Inequalities: Absolute Value
The properties that helped you solve equations were also very useful in solving inequalities in the previous hour. Graphing the solutions on a number line made the infinite number of possible values for the variables easier to see. The number line is also convenient when you are working with absolute value, an algebraic way of finding how far a number is from 0.
This hour, you will see how to find the solution of equations and inequalities that include absolute value. The problems will be limited to single variable expressions, as they were in the last hour, and you’ll see that most of the same properties you already know are used in these higher-level types of equations and inequalities.
Solving and Graphing Absolute Value Equations
The concept of absolute value is based on actual distance—how far a given point on the number line is from zero—but you’ll also see equations that include the absolute value of a variable or other expression. Before you learn how to solve these equations, let’s review the basics about absolute value.
Recall that the symbol for absolute value is two small vertical lines, | |, and that typically a number is inside:
|-9| → “the absolute value of negative 9”
JUST A MINUTE
When you learned about adding negative numbers in Hour 3, the absolute value of the number was used in the algebraic explanation. Example: (-7) + (-5) = -12 because the sum of two or more negative numbers is the negative sum of the numbers’ absolute values, or (-7) + (-5) → - (|-7| + |-5|) →> - (7 + 5) → -12.
Because -9 is 9 units away from 0, |-9| = 9.
|+9| is also 9 because +9 is 9 units away from 0.
The simplest way to know a number’s absolute value is to simply remove its sign:
|-9| = |+9| = 9
An open equation that includes absolute value follows:
|x| = 6
As with all open equations, your job is to find the value of the variable that makes the open equation a true equation. What can x be in this open equation? Another way to ask the same question: What number is 6 units away from 0?
The two possibilities are that x can be -6 or +6 because if you put either -6 or +6 into the original equation, you get a true statement:
|-6| = 6 and |+6| = 6
Also, both -6 and +6 are 6 units away from 0. No matter how you look at it, both numbers are the solution to |x| = 6, and this solution can be written as x = 6 or x = -6.
However, the best way to write this equation and its solution follows.
Solve: |x| = 6
Solution: x = ±6
This gives the solution in its most efficient form. You will hear it read aloud as “x equals positive or negative 6” or as “x equals plus or minus 6.”
Graphing the solutions to this equation on a number line is simply putting a darkened circle on the points -6 and +6—there would be no heavy line shading because the solutions are two individual points.

The graph of the solutions for absolute value equations can be shown on a real number line. Both solution values may not fit on the line unless the intervals are adjusted, as in the case of -14 and +14. Instead of numbering each mark with whole numbers, the line could have a scale of 5 with each mark labeled as -15, -10, -5, 0, +5, +10, and +15. This allows -14 and +14 to be shown as darkened circles slightly to the right of -15 and to the left of +15, respectively.
A similar absolute value equation and its solution follow:
Solve: |c| = 14
Solution: c = ±14
Again, the graph is two darkened circles on -14 and +14.
Now consider a more complex equation:
|x + 8| = 10
If this were written in words, it would be asking, “What values of x, when added to 8, are 10 units away from 0?” That is a rather confusing question, but the answer is easy to find with algebra.
The algebraic method relies on what you learned in the easier equation, so look at it again:
The solution of |x| = 6 is x = ±6, which can also be written as x = -6 or x = +6, and this is the form that helps you solve the more complex equation.
Solve: |x| = 6
Solution: x = -6 or x = +6
Apply this same process to |x + 8| = 10.
Solve: |x + 8| = 10
Solution: x + 8 = -10 or x + 8 = +10
Notice that the expression inside the absolute value symbol is set equal to the positive and negative values of 10. You now have two equations to solve, and each gives a solution of the original problem. The solution steps follow:
Solve: |x + 8| = 10
Solution: x + 8 = -10 or x + 8 = +10
Solving each equation gives the two solutions:
x + 8 = 10
x + 8 - 8 = 10 - 8
x = 2
or: x + 8 = -10
x + 8 - 8 = -10 - 8
x = -18
x + 8 - 8 = 10 - 8
x = 2
or: x + 8 = -10
x + 8 - 8 = -10 - 8
x = -18
To check, put each value of x into the original equation:
|x + 8| = 10 → |2 + 8| = 10 → |10| = 10 → 10 = 10;
|x + 8| = 10 → |-18 + 8| = 10 → |-10| = 10 → 10 = 10;
|x + 8| = 10 → |-18 + 8| = 10 → |-10| = 10 → 10 = 10;
Therefore, x = 2 and x = -18 are the solutions to the equation. The graph on a number line would be darkened circles at -18 and +2.
PROCEED WITH CAUTION
The checking process must be done carefully with absolute value equations. Be sure you substitute each of the two solutions into the original absolute value form because you might have made an error in the first step when you created the two new equations.
The solution to a simple equation like |a| = 5 is a = ±5, which can be done mentally, but if what is inside the absolute value bars is a more complex expression, always show the steps, beginning with the creation of the two equations. Another example of the more complex type is shown here:
Solve: |d - 7| = 5
Solution: d - 7 = 5 or d - 7 = -5
Solving each equation gives the two solutions:
d - 7 = 5
d - 7 + 7 = 5 + 7
d = 12
or: d - 7 = -5
d - 7 + 7 = -5 + 7
d = 2
d - 7 + 7 = 5 + 7
d = 12
or: d - 7 = -5
d - 7 + 7 = -5 + 7
d = 2
To check, put each value of d into the original equation:
|d - 7| = 5 → |12 - 7| = 5 → |5| = 5 → 5 = 5;
|d - 7| = 5 → |2 - 7| = 5 → |-5| = 5 → 5 = 5;
|d - 7| = 5 → |2 - 7| = 5 → |-5| = 5 → 5 = 5;
Therefore, d = 12 and d = 2 are the solutions to the equation. Graphing these solutions would be darkened circles at +2 and +12.
Now try to solve these absolute value equations, checking your answers on page 290.
1. |a| = 4
2. |b + 5| = 8
3. |x - 4| = 6
PROCEED WITH CAUTION
Every absolute value equation has two solutions, and the more complex the variable side of the equation is, the more steps you need to show in finding the solution. Resist the temptation to do a lot of the work mentally. Solving two equations can be confusing, so show as many of the small steps as possible, to avoid careless errors.
Solving absolute value equations follows the same rules as solving any basic equation, with the important first step of writing the two new equations and then solving each one to find the two solutions. As you’ll see in the next section, solving absolute value inequalities builds upon the skills you already have for solving basic inequalities.
Solving and Graphing Absolute Value Inequalities
Moving on up the ladder of solving problems that include absolute value, the next step brings you to inequalities. Let’s begin with a basic absolute value inequality and its solution:
|x| < 7
In words: “The absolute value of x is less than 7.”
In other words: “What values of x are less than 7 units away from zero?”
This problem can most easily be solved with the visual help of a graph on the number line. There won’t be just two points on this graph—there are many solutions to this inequality. In fact, all the numbers from 0 up to +7 and all the numbers from -7 to 0 will work. The following graph shows this solution: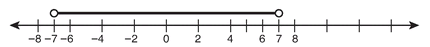
Each of the numbers on the graphed line segment makes this inequality true. The circles are open on -7 and +7 because they are not included in the solution: |-7| is equal to 7, not less than 7, so -7 must be excluded, and the same is true for |+7|. But every number—all the fractions, decimals, integers—from just above -7 up to +7 will work and are therefore on the solution graph.
Even though the graph shows you the answers to this simple inequality, the algebraic method is, of course, the better way to solve any absolute value inequality. The process is much like the one you know for solving absolute value equations, so you are really just refining those skills. And the solution will be written in algebraic form, which is far more efficient than “all the numbers between -7 and +7.”
Let’s solve the same absolute value inequality using algebra:
|x| < 7
If this problem was an absolute value equation, such as |x| = 7, you’d know the drill: the two new equations are x = -7 and x = +7, and the preferred form for the solution is x = ±7. You can do that mentally.
With an absolute value inequality, you also solve two new inequalities, but you must be careful how you write them:
One will be x < 7; the other will be x > -7.
This makes sense if you look back at the graphed solution line. But it is a process that you need to learn and use without hesitation and without having to make the graph.

Explaining the process of writing the two new inequalities is much more complex than the process itself. Practice it a few times, and you’ll see that it’s not difficult.
The easiest way is to memorize and follow this plan:
To create the two new inequalities, first write the problem “as it is,” but without the | | symbol, and then write the problem with the inequality reversed and the sign of the number on the right side reversed.
Here’s the process, worked out with an explanation:
Solve: |x| < 7
Solution: x < 7 and x > -7 are the new inequalities. Because both of these inequalities must be true at the same time, the solution is written in interval form, based on combining both inequalities:
x > -7 can be written as -7 < x. Because x < + 7, these both combine to make the interval -7 < x < +7, and this is the final solution.
Looking at the graph of this absolute value inequality, the interval solution -7 < x < +7 exactly matches the graph and can be read as “-7 is less than x, which is less than +7.”
The following example includes only the solution steps:
|a| ≤ 3
PROCEED WITH CAUTION
Be careful as you write the new inequalities—especially the second one, with its reversed inequality symbol and its reversed sign on the number on the right side of the inequality. The wrong sign or symbol will lead to a wrong solution.
Solution: a ≤ 3 and a ≥ -3 are the new inequalities; the combined inequality solution is -3 ≤ a ≤ 3 and the graph follows:

When the inequality includes a more complex expression within the absolute value symbol, the new inequalities are created with the same process. Solving these new problems just takes a little more work, but it is very similar to the inequality work you did in Hour 19. Some examples follow:
|x - 3| < 5
Solution: x - 3 < 5 and x - 3 > -5 are the new inequalities, solved in the following:
x - 3 < 5
x - 3 + 3 < 5 + 3
x < 8
and
x - 3 > - 5
x - 3 + 3 > - 5 + 3
x > -2
x - 3 + 3 < 5 + 3
x < 8
and
x - 3 > - 5
x - 3 + 3 > - 5 + 3
x > -2
Combining the two solutions, -2 < x < 8.
JUST A MINUTE
Remember that an open circle on the endpoint of a graph means that the number is not included in the solution. A darkened circle means it is a part of the solution, along with the rest of the darkened line: < and > have open circles; ≤ and ≥ have darkened circles.
The following is the graph: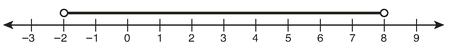
Now try to solve these absolute value inequalities. Graph their solutions, and check your answers on page 290.
4. |x| ≤ 5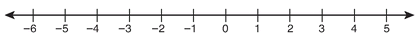
5. |a - 4| < 3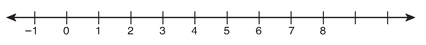
All the absolute value inequalities so far have included either < or ≤ as their relation. A variation in the final solution process comes into play when the > and ≥ inequalities are used, as you’ll see in the next examples.
Beginning with a basic inequality, you use the same process to write the two new inequalities:
|x| > 5
Solution: x > 5 or x < -5 are the new inequalities, and they need no further work. However, when you graph these solutions, something looks different: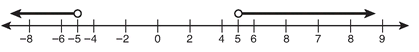
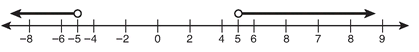

The solution of > and ≥ inequalities have two parts that are both inequalities, and they are most easily seen if you graph them on a number line.
The solution has two parts on the graph, and between these is open space. Choose a point in that open space—let’s use 2—and put it into the original inequality:
|2| > 5 → 2 > 5 → False
This shows that all the numbers in the open space are not solutions of the inequality. If you put any number from either of the graphed lines into the original problem, you will get a true statement because those lines do represent the solution to this inequality.
The following slightly more complex inequality will have a similar solution that can be graphed with two separate lines.
|x - 4| > 3
Solution: The new inequalities are created as before, and for this problem, they are x - 4 > 3 or x - 4 < -3. The solution steps follow:
x - 4 > 3
x - 4 + 4 > 3 + 4
x > 7
or
x - 4 < -3
x - 4 + 4 < -3 + 4
x < 1
x - 4 + 4 > 3 + 4
x > 7
or
x - 4 < -3
x - 4 + 4 < -3 + 4
x < 1
When the solutions are graphed, the lines form two separate sets of numbers that are solutions of the original inequality:

The open space between the two graphed lines shows the numbers that are not solutions of the original inequality.
Now try to solve these absolute value inequalities. Graph their solutions, and check your answers on page 291.
6. |x| ≥ 2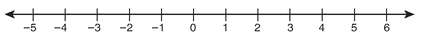
7. |b + 4| > 4
Your ability to solve equations and inequalities that include absolute value expressions pushes your algebra skills to an advanced level as it expands your mind’s ability to process increasingly complex ideas. Just as this hour has built upon your equation-solving abilities, the next section exposes you to new ways of looking at graphing lines on the (x,y) coordinate axes that you first saw in Hour 15.
Graphing Inequalities with Two Variables
The graphs of single-variable equation solutions can be drawn on a number line, as you have been doing for the past few hours. When equations have two variables—typically x and y—that are part of a general type of equation like y = mx + b, their solutions can be graphed as ordered pairs and the line that connects these ordered pairs.
GO TO ◀
Recall that y = mx + b is the slopeintercept form of a line that has a slope m and a y-intercept b. The line y = 2x + 6 has a slope—the ratio of rise to run—of 2 and a y-intercept of 6. The intercepts are (0,6) and (-3,0). See Hour 15 for a review of graphing lines.
For the final part of this hour, let’s look at solving some two-variable inequalities, such as the following:
y ≤ 2x - 4
In the same way you began when learning how to solve other inequalities, look at this problem written instead as an equation:
y = 2x - 4
It is in the slope-intercept form of y = mx + b, where m is the slope and b is the y-intercept. The slope of this line is 2, and the y-intercept is -4. The following graph on the x- and y-axes shows this equation’s line:

Every point on this line is a solution of the equation y = 2x - 4, and there are an infinite number of solutions because there are an infinite number of points on the line. This review of graphing the solution of an equation helps you see all those solutions (ordered pairs) more easily.
Now return to the inequality y ≤ 2x - 4.
Its graph is based on the graph of the line y = 2x - 4. However, the inequality includes even more points than are on the line. Your goal is to find all the (x,y) values that make this inequality a true statement. Because ≤ means “less than or equal to,” you know that the line shows all the “equal to” points.
Where are the “less than” ordered pairs?
The best way to find them is to choose a specific point that is not on the line and check it in the original inequality. If it makes a true statement, all the points in that region of the graph will make a true statement.
Let’s use the ordered pair (5,0). It lies to the right of the line. Does it make a true statement? Put 5 in for x and 0 in for y in the original inequality:
y ≤ 2x - 4 → 0 ≤ 2 · 5 - 4 → 0 ≤ 10 - 4 → 0 ≤ 6 → True

If an ordered pair from one side of the graphed line makes a true statement when put into the original inequality, then all the ordered pairs on that side of the line will also make a true statement. They are all solutions of the inequality.
Yes, the ordered pair (5,0) is a solution for this inequality. All the ordered pairs to the right of the line will make a true statement when put into the original inequality. None of the ordered pairs on the left side will make a true statement. Let’s confirm this using a chosen point, (0,3). Put 0 in for x and 3 in for y in the original inequality:
y ≤ 2x - 4 → 3 ≤ 2 · 0 - 4 → 3 ≤ 0 - 4 → 3 ≤ -4 → False
To show the graph of all the ordered pairs that are solutions of the inequality, you shade in the area of the graph lightly to the right of and below the graphed line, as shown in the following: 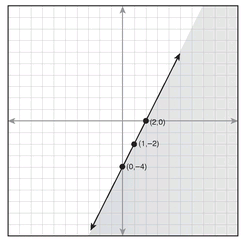

The final example shows the solution of another inequality with two variables:
y > x + 3
First, graph the line from the equation y = x + 3. This line has a slope of 1 and y-intercept of 3, with key points (0,3), (1,4), and (-3,0); the graph is shown here: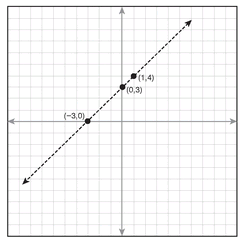

In the graphs on the real number line for inequalities such as x > 3, the open circle on +3 shows that 3 is not a part of the solution, but the heavy line extending to the right of +3 shows all the numbers that are the solution. In the same way, lines on (x,y) graphs are dashed, not solid, if the inequality is < or >. This shows that the ordered pairs on the line are not part of the solution, but the shaded area is the solution.
Notice that the line is not drawn as a solid line, but is dashed. This is because the original inequality was >, not ≥, so the ordered pairs on this line are not actually part of the solution.
Now choose a point to the right of the line, such as (0,2), and put 0 in for x and 2 in for y in the original inequality:
y > x + 3 → 2 > 0 + 3 → 2 > 3 → False
This shows that all the ordered pairs on the right side of the line will make false statements, so the shading should go on the left side. To confirm this, choose an ordered pair on the left, such as (-2,4), and put -2 in for x and 4 in for y in the original inequality:
4 > -2 + 3 → 4 > 1 → True
This confirms that all the ordered pairs to the left of and above the dashed line are solutions, so that region should be shaded, as follows:

Now try to graph the solution of the following inequalities, checking your answers on pages 291-292.
8. y < 3x - 6; slope is 3 and y-intercept is -6

9. y ≥ 2x + 6; slope is 2 and y-intercept is 6

Graphing the lines at the heart of two-variable inequalities gives you the boundary that separates the two regions of the (x,y) ordered pairs; one area has all the solutions, and the other area has none. This allows you to easily identify whether any specific ordered pair is a solution of the inequalit y.
Answers to Sample Problems
1.
|a| = 4 → a = ± 4
2.
|b + 5| = 8 → b + 5 = 8 or b + 5 = -8 b + 5 = 8
b + 5 - 5 = 8 - 5
b = 3
b + 5 = -8
b + 5 - 5 = -8 - 5
b = -13
b = -13 or 3
b + 5 - 5 = 8 - 5
b = 3
b + 5 = -8
b + 5 - 5 = -8 - 5
b = -13
b = -13 or 3
3.
|x - 4| = 6 → x - 4 = 6 or x - 4 = -6 x - 4 + 4 = 6 + 4
x = 10
x - 4 + 4 = -6 + 4
x = -2
x = -2 or 10
x = 10
x - 4 + 4 = -6 + 4
x = -2
x = -2 or 10
4. |x| ≤ 5 → x ≤ 5 and x ≥ -5 → combine to give the interval -5 ≤ x ≤ 5

5.
|a - 4| < 3 → a - 4 < 3 and a - 4 > -3 a - 4 + 4 < 3 + 4
a < 7
a - 4 + 4 > -3 + 4
a > 1
a > 1 and a < 7 combine to give the interval 1 < a < 7
a < 7
a - 4 + 4 > -3 + 4
a > 1
a > 1 and a < 7 combine to give the interval 1 < a < 7
6. |x| ≥ 2 → x ≥ 2 or x ≤ -2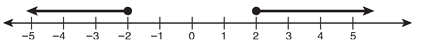
7.
|b + 4| > 4 → b + 4 > 4 or b + 4 < -4 b + 4 - 4 > 4 - 4
b > 0
b + 4 - 4 < -4 - 4
b < -8
b > 0
b + 4 - 4 < -4 - 4
b < -8
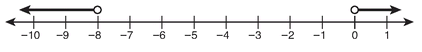
8. y < 3x - 6; slope is 3 and y-intercept is -6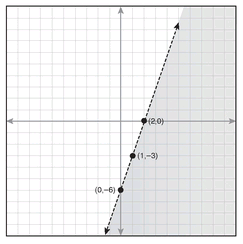

9. y ≥ 2x + 6; slope is 2 and y-intercept is 6

Review
Hour’s Up!
Based on what you’ve learned in Hour 20, find the solutions for the following absolute value equations and inequalities. Check your answers with the solution key in Appendix B.
1. |x| = 9
a. x = 9
b. x = -9
c. x = ±9
d. x < 9
2. |c - 6| = 7
a. c = 1 or -13
b. c = -1 or 13
c. c = 1 or 13
d. c = -1 or -13
3. |x + 2| = 8
a. x = -10 or -6
b. x = 10 or 6
c. x = 10 or -6
d. x = -10 or 6
4. |x| < 4
a. x < 4
b. x < -4
c. -4 < x < 4
d. 4 < x < -4
5. |a + 7| ≤ 3
a. 4 ≤ a ≤ -10
b. -10 ≤ a ≤ -4
c. a ≤ 10
d. a ≤ -10
6. |x - 3| ≤ 1
a. 2 ≤ x ≤ 4
b. -2 ≤ x ≤ 4
c. 2 ≤ x ≤ -4
d. -2 ≤ x ≤ 4
7. |a - 2| < 7
a. 5 < a < 9
b. -5 < a < -9
c. -5 < a < 9
d. 5 < a < -9
8. |c| > 3
a. c < -3 or c > 3
b. c < 3 or c > -3
c. -3 < c < 3
d. c < -3
9. |x - 8| ≥ 6
a. x ≤ -2 or x ≥ 14
b. 2 ≤ x ≤ 14
c. x ≥ 2 or x ≤ 14
d. x ≤ 2 or x ≥ 14
10. |x + 2| > 4
a. -6 < x < 2
b. x < 6 or x > 2
c. x < -6 or x > 2
d. x < -2 or x > 6
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.
