Hour 14
Ratios and Proportions: Mixture and Work Problems
Ratios, proportions, and percents help you solve many different practical problems, from adjusting a recipe’s ingredients to comparing the time you spend on the phone at work to the time you spend in meetings. In this next hour, you will learn additional ways percents are useful when analyzing change, whether it’s the change in the price of an item that’s now on sale or the change in your utility bills from one month to the next. You will also be able to calculate not only the amount of different items needed to make a certain mixture, but also the amount of time it will take to get a job done if others help you. Algebra is the key to all these real-life problems, even though they are very different situations.
Solving Percent of Increase or Decrease Problems
The  proportion gives you an efficient way to work with many percent problems. But it doesn’t apply in some situations where percents often occur, such as when you are comparing prices, enrollment numbers, business expenses, or other statistics and want to know the percent of change.
proportion gives you an efficient way to work with many percent problems. But it doesn’t apply in some situations where percents often occur, such as when you are comparing prices, enrollment numbers, business expenses, or other statistics and want to know the percent of change.
Consider the following problem:
Your cable TV bill is now $90 per month. Last year you lived in another city and paid only $72 for the same service. What is the percent of increase for your cable service?
Solution: This percent problem is about change, and even though you can use the proportion from Hour 13 for many percent calculations, the following proportion helps you find the percent of change from an original amount to a new amount:
In the cable TV example here, you know the original price, $72, and the new price, $90. The proportion uses the original price, but it also uses the change in price—not the new price. Subtraction gives you the change in price:
90 -72 = 18
You can now put all the numbers into the proportion, using x for the unknown % of change:
The cross-product process helps you create the next equation:
18 · 100 = 72 · x
1,800 = 72x
1,800 = 72x
Dividing both sides by 72:
25 = x
Your cable bill has increased 25%. you want to calculate percent of change, whether it is an increase or a decrease.
you want to calculate percent of change, whether it is an increase or a decrease.
If you always find the change in price by using “new price” minus “old price,” the percent answer will be positive if it was an increase, and it will be negative if it was a decrease, as shown in the next example:
Your employer had to cut back everyone’s hours this month to save on expenses. You now work 20 hours a week, and you were working 25 hours each week. What is the percent of change in your hours per week?
Solution: This problem is about work schedule change, not price change, but the change proportion still works. It can be shortened so that it applies to all percent-of-change problems:
Put your numbers in the proportion. Use 25 for “original” because you were working 25 hours a week before the slowdown. What is “change”? Remember to use “new” minus “old” to find “change.” Your “new” schedule is 20 hours, and your “old” was 25.
new - old → 20 - 25 = 20 + (-25) = -5
The numbers can now be put into the proportion: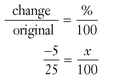
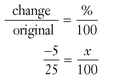
The cross-product creates the equation:
-5 · 100 = 25 · x
-500 = 25x
-500 ÷ 25 = 25x ÷ 25
-20 = x
-500 = 25x
-500 ÷ 25 = 25x ÷ 25
-20 = x
Your hours per week have decreased 20% because a negative percent shows a decrease, just as a positive percent shows an increase in your cable bill.
Let’s look at a utility bill comparison:
Last month your electricity bill was $68. The month before that it was $80. What is the percent of change?
Solution: Find the change by subtracting “new” minus “old.” Careful with this one—the words make it a bit difficult to know which bill is new and which is old. Your “new” bill is $68, and your “old” bill was $80:
new - old → 68 - 80 = -12
Put the numbers into the proportion: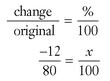
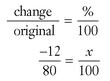
The cross-product gives the following equation:
-12 · 100 = 80 · x
-1,200 = 80x
-1,200 ÷ 80 = 80x ÷ 80
-15 = x
-1,200 = 80x
-1,200 ÷ 80 = 80x ÷ 80
-15 = x
Your utility bill decreased 15%, from $80 to $62.
The two proportions for all percent problems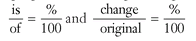 are very easy to use, and you should memorize them. It helps that they both have the
are very easy to use, and you should memorize them. It helps that they both have the 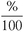 after the equals signs. You will need to remember the is/of and the change/original ratios before the equals signs, but writing both proportions a few times will help keep them in your memory.
after the equals signs. You will need to remember the is/of and the change/original ratios before the equals signs, but writing both proportions a few times will help keep them in your memory.
The percent-of-change proportion can lead to wrong answers if you forget that the first denominator must be the original number. Many people mistakenly use the new number. If you remember to always use the original, this proportion will be invaluable in finding percent of change, as well as finding other terms of the proportion if you already know the percent of change, as in the following example:
Enrollment at a local college increased 20% this year compared to a year ago. There are 640 more students this year than last. How many students were enrolled last year?
Solution: Use the percent-of-change proportion. change %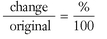
You already know the “change” is 640, the percent is 20, and x is the unknown percent, so these terms can be put into the proportion:

The cross-product creates the equation:
64,000 = 20x
64,000 ÷ 20 = 20x ÷ 20
3,200 = x
64,000 ÷ 20 = 20x ÷ 20
3,200 = x
There were 3,200 students enrolled last year.
Now try these percent of change problems, checking your answers on page 174.
1. The monthly rent for your apartment went up from $560 to $644. What is the percent of increase?
2. A pair of shoes you bought regularly costs $48, but today it’s on sale for only $36. What is the percent of change?
3. You saved $15 when you bought a sweater today at a store that was having a sale of 25% off regular price. What was the regular price of the sweater?
Proportions have played a large role in the percent work so far this hour. The mixture problems that follow show that algebra comes in handy in lots of places, from labs to grocery stores.
Setting Up and Solving Mixture Problems
When different items are combined to make a mixture, whether it’s a saline solution or granola cereal, percents are often an important part of finding the equation you need to solve.
Let’s look first at a saline solution problem. A chemist in a lab has 20 liters of a 25% saline solution. How many liters of water should be added to make a solution that is 20% saline?
Drawing the liters of solution as barrels is helpful. In each mixture problem, the percents are changed to decimal numbers. The lid of each barrel shows the percent of that barrel’s salinity, written in decimal form. The lower part of each barrel shows the number of liters in that barrel.
JUST A MINUTE
Percents can always be written in decimal form by moving the decimal point two places to the left: 85% = .85; 5% = .05; 800% = 8. Decimal numbers can always be written as percents by moving the decimal point two places to the right: .18 = 18%; .01 = 1 %; 2 = 200%.
In this problem, the 25% saline solution (in the first barrel, with .25 on the lid) will have water (in the second barrel) added to make a new barrel. Water is 0% saline, so 0 is on the lid of the second barrel. The new barrel needs to be 20% saline, so .20 is on the lid. The chemist has 20 liters in the first barrel and will be adding x liters in the second barrel to make a new barrel that will hold 20 + x liters. The barrels are shown here: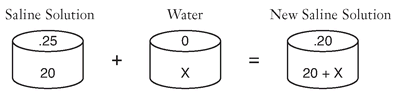

This illustration lets you see the problem clearly, and the equation is easily written from the barrels. You multiply the numbers in each barrel because “of” always indicates multiplication:

.25 · 20 + 0 · x = .20 · (20 + x)
5 = .20 · 20 + .20 · x
5 = 4 + .2x
5 - 4 = 4 + .2x - 4
1 = .2x
1 ÷ .2 = .2x ÷ .2
5 = x
5 = .20 · 20 + .20 · x
5 = 4 + .2x
5 - 4 = 4 + .2x - 4
1 = .2x
1 ÷ .2 = .2x ÷ .2
5 = x
JUST A MINUTE
Decimal numbers that end in a zero to the right of the decimal point can be written with or without the zero(s): .50 = .5; 3.00 = 3.
5 liters of water need to be added to make a 20% saline solution.
The following mixture problem shows how to increase the acidity in a solution. The method is similar to the saline problem, and the barrels will help you write the equation.
A chemist in a lab has 30 liters of a 20% acidic solution. How many liters of acid should be added to make a solution that is 40% acidic?
The 20% acid solution (in the first barrel, with .20 on the lid) will have acid (in the second barrel) added to make a new barrel. Acid is 100% acidic, and 100% = 1 in decimal form, so 1 is on the lid of the second barrel. The new barrel needs to be 40% acid, so .40 is on the lid. The chemist has 30 liters in the first barrel and will be adding x liters in the second barrel to make a new barrel that will hold 30 + x liters. The barrels are shown here:

The equation can now be written from the barrels’ labels:
.20 · 30 + 1 · x = .40 · (30 + x)
JUST A MINUTE
When an equation has a variable on both sides of the equals sign, move the variable with the smaller coefficient: 2x + 5 = 5x - 7 → 2x + 5 - 2x = 5x - 7 - 2x → 5 = 3x - 7 → 5 + 7 = 3x - 7 + 7 → 12 = 3x → x = 4.
6 + x = .40 · 30 + .40 · x
6 + x = 12 + .4x
6 + x - .4x = 12 + .4x - .4x
6 + .6x = 12
6 + .6x - 6 = 12 - 6
.6x = 6
.6x ÷ .6 = 6 ÷ .6
x = 10
6 + x = 12 + .4x
6 + x - .4x = 12 + .4x - .4x
6 + .6x = 12
6 + .6x - 6 = 12 - 6
.6x = 6
.6x ÷ .6 = 6 ÷ .6
x = 10
Adding 10 liters of acid will give a new solution that is 40% acidic.
The barrel system is an efficient way to organize the information in a rather complex real-life situation to be used in an equation. When percents are involved, they are changed to decimals. In the next example, dollars are the units, along with pounds instead of liters, but the barrels help you see that it’s really just an algebra problem that is easily solved.
Consider a granola mixture problem:
A store’s produce department sells granola in bulk and makes its own custom mixture from a combination of granola and nut clusters. The granola costs $2 per pound, and the nut clusters cost $5 per pound. They want to make 60 pounds of the custom mixture that will cost $3 per pound. How much of the granola and nut clusters will it take?
Solution: The first barrel is for the granola, and the second barrel is for nut clusters. The new mixture is in the barrel after the equals sign. This problem doesn’t give an amount for either of the ingredients, but you do know there will be a total of 60 pounds in the new mixture barrel. If you let x be the pounds of granola, then 60 - x is the pounds of nut clusters. (Adding x and 60 - x equals 60, which is the total you want in the new barrel.) The barrels can be labeled as shown here:

Write the equation from the labels on the barrels:
2 · x + 5 · (60 - x) = 3 · 60
2x + 5 · 60 - 5 · x = 180
2x + 300 - 5x = 180
-3x + 300 = 180
-3x + 300 - 300 = 180 - 300
-3x = -120
-3x ÷ -3 = -120 ÷ -3
x = 40
2x + 5 · 60 - 5 · x = 180
2x + 300 - 5x = 180
-3x + 300 = 180
-3x + 300 - 300 = 180 - 300
-3x = -120
-3x ÷ -3 = -120 ÷ -3
x = 40
Because x is the pounds of granola, it will take 40 pounds of granola and 20 pounds (from 60 - x) of the nut clusters to make 60 pounds of the custom mixture.
Now try the following mixture problems, checking your answers on pages 174-175.
4. How many liters of water should be added to 10 liters of 40% acidic solution to make a new solution that is 25% acidic?
5. You want to make a new candy mixture from jelly beans and chocolate candies. The jelly beans cost $2 a pound, and the chocolate costs $5 a pound. How much of each candy will you need to make 30 pounds of the new mixture that costs $4 a pound?
Mixture problems can most efficiently be shown as barrel drawings that lead you directly to the algebraic equation. Work problems also have a specific method that helps you write the equation. Let’s finish this hour learning about the effect of people working together to get a job done.
Setting Up and Solving Work Problems
Setting up work schedules for a large business or a small shop has many elements that need to be considered. Algebraic equations are a big part of the decision making that goes into analyzing how long it takes more than one person to do a certain job.
In this last part of Hour 14, you may be surprised when you see how long it takes two people to do a job that they usually do separately.
Consider the following problem:
If it takes you 20 minutes to load packages onto the delivery truck and it takes Joe 30 minutes to do the same loading job, how long will it take if you both work together?
Solution: The method used to solve this type of problem is based on work rates. The following general work equation helps you find the time (t) it takes for two people—a and b—to do a job when they work together.
The variables a and b represent the time it takes each person to do the given job when they are working alone. Putting in the example’s numbers creates the following equation: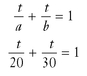
PROCEED WITH CAUTION
Recall that a proportion is two ratios that are equal to each other. The equations in these work-related problems are not proportions: the two ratios are not equal to each other—they are added to equal 1.
To solve for t, you need to move the 20 and the 30 to the other side of the equals sign. This problem isn’t a proportion, so the cross-product method won’t help solve this equation.
The key to isolating the variable t is the multiplication property of equality, which happens to be the same property that helps you solve proportions. If you multiply both sides of the equation by the least common denominator (LCD) for 20 and 30, the equation will be in a much simpler form.
30 is not the LCD because 20 is not a factor of 30. The easiest way to find the LCD for 20 and 30 is to multiply the larger number, 30, by 2. This equals 60, and 20 is a factor of 60, so the LCD is 60. The solution steps for the equation are shown here: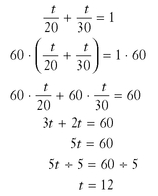
Working together, it will take only 12 minutes for you and Joe to load the delivery truck, as long as you both work at your regular speeds.
The answer to this type of work-together problem is usually a fraction, as in the following example:
You work for the maintenance department of a large apartment building. Before new tenants move in, you paint the walls of each apartment. If you can paint all bedroom walls and ceiling in a two-bedroom apartment in three hours and another employee can paint the same number of walls and the ceiling in the same apartment in four hours, how long will it take if you both work together to paint one apartment?
Solution: The general work equation is used for this problem:

To find the LCD, multiply 4 times 2, which is 8. Since 3 is not a factor of 8, multiply 4 times 3, which is 12 and the LCD. Multiplying both sides of the equation by 12 will help you isolate the variable: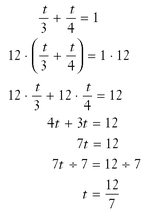
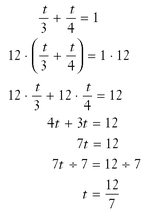
Using a calculator to divide 12 by 7 gives a decimal answer of about 1.7. The times in the problem are in hours, as is the answer, so it will take about 1.7 hours if you both paint the apartment together, or a little less than 2 hours.
The work equation can also be used if three or more people are all working together—the LCD may be a little harder to find, but it can be done. The equation for three workers would be as follows: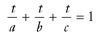
This problem-solving technique applies only to a job that can be done by more than one person at the same time, not an assembly-line type job where many lines of work are in progress. The ability to calculate the amount of time it takes for people to do a job working together instead of separately relies heavily on algebraic skills, and you have mastered them.
Now try these work problems, checking your answers on page 175.
6. When you work alone, it takes you 2 hours to mow the lawn on a rider mower. Your brother can mow it in 4 hours walking behind a self-propelled mower. How long will it take if you both work together?
7. You can vacuum the restaurant’s floor area after closing time in 10 minutes. Using an older vacuum cleaner that doesn’t work as well, your co-worker takes 15 minutes. If you both work together to get the job done, how long will it take?
Answers to Sample Problems
1. 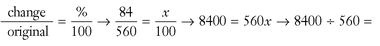 560x ÷ 560 → 15 = x. The percent of increase is 15%.
560x ÷ 560 → 15 = x. The percent of increase is 15%.
2. 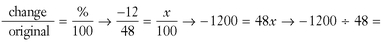 48x ÷ 48 → -25 = x. The percent of decrease is 25% (-25% is a decrease).
48x ÷ 48 → -25 = x. The percent of decrease is 25% (-25% is a decrease).
3. 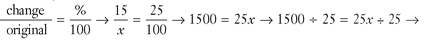 60 = x. The regular price of the sweater was $60.
60 = x. The regular price of the sweater was $60.
4. 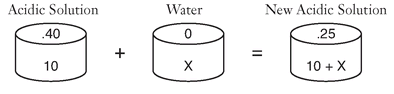

.40 · 10 + 0 · x = .25 · (10 + x)
4 = .25 · 10 + .25 · x
4 = 2.5 + .25x
4 -2.5 = 2.5 + .25x - 2.5
1.5 = .25x
1.5 ÷ .25 = .25x ÷ .25
6 = x
4 = .25 · 10 + .25 · x
4 = 2.5 + .25x
4 -2.5 = 2.5 + .25x - 2.5
1.5 = .25x
1.5 ÷ .25 = .25x ÷ .25
6 = x
6 liters of water need to be added.
5. 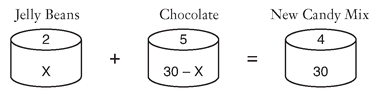

2 · x + 5 · (30 - x) = 4 · 30
2x + 5 · 30 - 5 · x = 120
2x + 150 - 5x = 120
-3x + 150 = 120
-3x + 150 - 150 = 120 -150
-3x = -30
-3x ÷ -3 = -30 ÷ -3
x = 10
2x + 5 · 30 - 5 · x = 120
2x + 150 - 5x = 120
-3x + 150 = 120
-3x + 150 - 150 = 120 -150
-3x = -30
-3x ÷ -3 = -30 ÷ -3
x = 10
10 pounds of jelly beans and 20 pounds of chocolate
6. 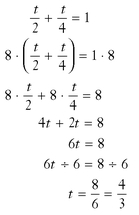
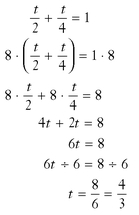
7. 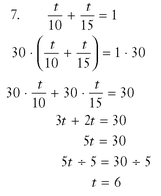
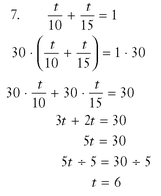
It will take 6 minutes if you both work together.
Review
Hour’s Up!
Based on what you’ve learned in Hour 14, do the following problems. Check your answers with the solution key in Appendix B.
1. Your water bill last month was $24. The month before that, it was $20. What is the percent of change?
a. Increase of 10%
b. Increase of 20%
c. Decrease of 16%
d. Decrease of 20%
2. The monthly rent for your new apartment is $605. You paid $550 each month for your old apartment. What is the percent of change?
a. Increase of 9%
b. Decrease of 9%
c. Decrease of 10%
d. Increase of 10%
3. You bought a pair of boots on sale for $90. The regular price was $120. What was the percent of change?
a. Decrease of 25%
b. Increase of 25%
c. Decrease of 33%
d. Increase of 33%
4. Your boss needs you to work more hours next week to help cover another employee who will be on vacation. This week you are working 25 hours, and next week you are scheduled for 30 hours. What is the percent of change?
a. Increase of 17%
b. Decrease of 17%
c. Increase of 20%
d. Decrease of 20%
5. How much acid should be added to 20 liters of 25% acidic solution to make a new solution that is 40% acidic?
a. 5 liters
b. 10 liters
c. 15 liters
d. 20 liters
6. How much water should be added to 50 liters of 30% saline solution to make a new solution that is 20% saline?
a. 10 liters
b. 15 liters
c. 20 liters
d. 25 liters
7. Pecans and walnuts will be combined to make 40 pounds of nut mixture that costs $6 per pound. The pecans cost $8 per pound, and the walnuts cost $3 per pound. How many pounds of pecans and of walnuts will it take to make the nut mixture?
a. 24 pounds of pecans, 16 pounds of walnuts
b. 16 pounds of pecans, 24 pounds of walnuts
c. 20 pounds of pecans, 20 pounds of walnuts
d. 10 pounds of pecans, 30 pounds of walnuts
8. You can load 600 boxes into the semi-trailer in 30 minutes. Your co-worker is very fast and takes only 15 minutes to do the same job. How long will it take if you both load the truck together?
a. 5 minutes
b. 10 minutes
c. 12 minutes
d. 15 minutes
9. It takes you 40 minutes to wash your car by hand in the drive-way. Your brother washes it in 30 minutes. How long will it take if you both wash it together?
a. About 10 minutes
b. About 13 minutes
c. About 17 minutes
d. About 20 minutes
10. You can unload and stack a cord of wood in 2 hours. Your brother takes 3 hours to do the same job. How long will it take if you both work together?
a. 1.2 hours
b. 2.2 hours
c. 2.4 hours
d. 2.6 hours
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.
