Hour 7
Polynomials: Exponents and Basic Operations
You learned how to simplify algebraic expressions and solve equations, two important concepts that set algebra apart from basic arithmetic. The real-life problems you can now solve include car-rental cost comparisons and how long it takes to reach a savings goal. But you have been limited so far to one-dimensional problems. Many situations in life require two or three dimensions, from finding the square footage of a room when ordering new carpet, to calculating the cubic feet in your home to get the most efficient new furnace and air-conditioner.
Fully understanding algebra involves expanding your mind beyond a single dimension. From now on, many of the concepts are more intangible than the first six hours have been. Your goal is to be able to solve equations and work with expressions that are on a higher level. Taking it one hour at a time, building on the properties and processes you have learned so far, you can reach that goal.
Exponents
Think about the expression 3x + 4x. To simplify it, you would write 3x + 4x = 7x because you know how to combine like terms. 7x is a very efficient way to describe 3x + 4x. Similarly, algebra has efficient ways to simplify factors that are multiplied, as in the next example:
x · x · x can be written x3
Notice that three x factors are multiplied, and the new expression x3 shows the x and a small 3 raised a little above the x. In x3, the x is called the base and the 3 is called the exponent or power. Numbers can also be the base, as in the following example:
8 · 8 · 8 · 8 can be written 84
STRICTLY DEFINED
An exponent, also called a power, is the small number that tells how many times the number below it (the base) is multiplied times itself. In a5, 5 is the exponent and a is the base. a5 is “a to the fifth power” or “a to the fifth.”
As you see, multiplying 8 times itself four times (which is a very large number!) is very efficiently written with a base of 8 and an exponent of 4.
To say these expressions aloud, x3 is “x to the third power” or shortened to “x to the third.” You will also hear it described as “x cubed.” 84 is “eight to the fourth power” or simply “eight to the fourth.”
An exponent of 2 is common. b2 is “b to the second power,” “b to the second,” or “b squared.” A variable or number with no exponent showing can be written with an exponent of 1. So x = x1, and you can say, “x is equal to x to the first power,” and 5 = 51, or “5 equals 5 to the first power.”
The exponent tells you the number of times the base is multiplied by itself. The following examples show the expanded and exponential forms of several expressions:
JUST A MINUTE
Remember that parentheses with no other operation indicate multiplication. They can also be used simply for emphasis, as in example h.
a. 2 · 2 · 2 · 2 · 2 · = 25
b. c · c · c · = c 3
c. (4)(4)(5)(5)(5) = 42 · 53
d. 74 = 7 · 7 · 7 · 7
e. x3 · y2 = x · x · x · y · y
f. 5a4b3c = 5 · a · a · a · a · b · b · b · c
g. -3x5 = -3 · x · x · x · x · x
h. 6 · x · (-3) · x · x = -18x3
i. -2 · a · a · - 4 · a · b · b = 8a3b2
Now write the following expressions in expanded or exponential form, checking your answers on page 84.
1. 9 · 9 · 9 · 9 =
2. -6cd4 =
3. 5 · 5 · 5 · x · x · y =
4. 3 · a · (-3) · b · b =
Following the Order of Operations with Exponents
When algebraic expressions have more than one operation, you learned in Hour 1 that terms in parentheses are combined first. When exponents are included in an expression, they are next in the order, followed by multiplying and dividing from left to right. Adding and subtracting is then done from left to right.
The following examples show this sequence. Note especially what happens when parentheses are around different terms in these problems. The answers vary greatly, and it’s all due to where the parentheses are.
j. 2 · 32 = 2 · 9 = 18
k. (2 · 3)2 = (6)2 = 6 · 6 = 36
l. 2 + 32 = 2 + 9 = 11
m. (2 + 3)2 = (5)2 = 25
n. 22 + 32 = 4 + 9 = 13
o. 22 + 3 = 4 + 3 = 7
p. (-3)2 = (-3) · (-3) = 9
q. -32 = -(3·3) = -9
r. (3x)2 = (3x)(3x) = 9x2
s. 3x2 = 3 · x · x

Note carefully the importance of the parentheses in example r: the 3 inside the parentheses is squared to make 9. In example s, the 3 is not affected by the exponent 2—only the x is squared.
Many formulas used in medicine, finance, physics, and engineering include exponents. Being able to evaluate a formula when you are given values for the variables is the most common real-life application of exponents. The following examples show the correct substitutions and order of operations.
t. If a = 3 and b = 4, evaluate ab2.
Solution: 3 · 42 = 3 · 16 = 48
u. If a = 3 and b = 4, evaluate (ab)2.
Solution: (3 · 4)2 = (12)2 = 12 · 12 = 144
v. If x = 4 and y = 3, evaluate x2 - y2.
Solution: 42 - 32 = 16 - 9 = 7
w. If a = -2 and b = 5, evaluate 3a2 + 2b2.
Solution: 3(-2)2 + 2(5)2 = 3 · -2 · -2 + 2 · 5 · 5 = 12 + 50 = 62
x. If x = 2 and y = 3, evaluate 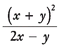 .
.
Solution: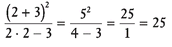
Now try the following problems. Check your answers on page 84.
5. 2 · 42 =
6. (2 · 4)2 =
7. 2 + 42 =
8. (2 + 4)2 =
9. -5 + (-2)3 =
10. If x = 2 and y = 4, evaluate (x + y)2 - x2 + y2.
11. If a = -3 and b = 5, evaluate  .
.
It’s time to define the key word in this hour’s title, polynomials. In fact, you’ve been working with polynomials all hour! Instead of learning a formal definition, look at the following examples to get a working knowledge of some big words that describe simple ideas.
STRICTLY DEFINED
Polynomials are sums of expressions that can include numerals, variables, and exponents in the terms. Monomials have only one term, binomials have two terms, and trinomials have three terms. The exponents must be whole numbers (no fractions or negative numbers), and polynomials cannot have any variables in the denominator. Therefore, (x + y) ÷ (2x - y) is not an example of a polynomial, but it is an algebraic expression that can be evaluated if you know the x and y values.
In this first example, c32 and 4a2 are each a kind of polynomial called monomials because they don’t include any adding or subtracting, only multiplication. 2x4 + 5 and 3x2 - 7x are both called binomials because they are made up of two monomial terms that are added or subtracted. A polynomial like 2x2 - 3x + 12 is called a trinomial because there are three monomial terms making one expression. Expressions with four or more terms are simply called polynomials.
The following table has examples of algebraic expressions and their descriptive names:

Simplifying polynomials follows the same rules you used last hour to solve equations. You already know how to simplify 7x + 2x + 5 to get 9x + 5. The 7x and the 2x terms can be added together because they are like terms—they both have the same variable x. The coefficients 7 and 2 sum to 9, so the result is 9x + 5.
Similarly, 7x2 + 2x2 = 9x2 because 7x2 and 2x2 are like terms. Notice, though, that the exponent didn’t change to a 4, and this is important: when like terms are added or subtracted, the exponent never changes. Like terms must have the same base and exponent, but their coefficients do not need to be the same.
JUST A MINUTE
Remember that the coefficient of a variable is the number in front of the variable, and if no number is shown, it is understood to be a 1. If the coefficients of two terms sum to zero, the entire term becomes a zero: -3x + 3x = 0 · x = 0. Note that the -3 and +3 (the coefficients of the variables x) sum to zero, so the entire term becomes a zero.
The following examples show how to simplify polynomials by first grouping the like terms and then combining them.
Simplify:
y. 6x2 + 5x - 2x2 + 3x = 6x2 - 2x2 + 5x + 3x = 4x2 + 8x
z. 3a3 + 7a - 2 - a3 + 7a = 3a3 - a3 + 7a + 7a - 2 = 2a3 + 14a - 2
Now try simplifying the following polynomials. Check your answers on page 84.
12. x4 - 3x3 + 4x4 + 2x3 + 4 =
13. 2a2 + 6b3 - 5a2 - 4 + 2b3 =
14. 3y + 3y2 + 5z + 3y =
15. 9xy - 3x3 + 6x3 - 9xy =
Adding and Subtracting Polynomials
The simplifying you did in problems 12 through 15 leads directly to learning how to add or subtract polynomials. You still need to look for like terms. The problems look a bit different than the simplifying problems do, but the addition and subtraction examples that follow show how easy the process is:
Add 2x3 - 3x2 + x + 5 and 8x3 + 3x2 + x - 7.
This problem can also be written as (2x3 - 3x2 + x + 5) + (8x3 + 3x2 + x - 7).
Solution: These two polynomials can be stacked vertically, or the similar terms in each can be grouped, as in examples w through z. The vertical method is shown first: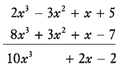
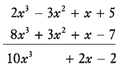
The grouping method is as follows:
2x3 + 8x3 - 3x2 + 3x2 + x + x + 5 - 7 = 10x3 + 2x - 2
Subtract 2x3 - 3x2 + x + 5 from 8x3 + 3x2 + x - 7.
Solution: Remember that subtraction must be done in the proper order. For example, to subtract 3 from 7, use 7 - 3 = 4, not 3 - 7 (which is -4). To subtract the first polynomial from the second one, be sure the second one is put first, before the subtraction sign.
GO TO ◀
Subtraction can be changed to addition if you change the signs of all the terms in the second expression. (See Hour 3.)
This problem can also be written as follows:
(8x3 + 3x2 + x - 7) - (2x3 - 3x2 + x + 5)
The subtraction sign becomes addition, but you must change each sign in the polynomial being subtracted, which is shown here: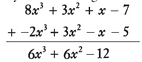
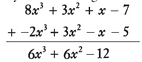
Subtraction can also be done by the grouping method:
(8x3 + 3x2 + x - 7) - (2x3 - 3x2 + x + 5) becomes an addition problem if you change all the signs in the second polynomial:
(8x3 + 3x2 + x - 7) + (-2x3 + 3x2 - x - 5)
The like terms can now be grouped and combined:
8x3 - 2x3 + 3x2 + 3x2 + x - x - 7 - 5 = 6x3 + 6x2 - 12
GO TO ◀
Refer to the sign rules in Hour 3 for adding positive and negative numbers when combining like terms.
As you can see, subtraction is more complex than addition, but following the process carefully and watching every sign as you work is the key to success with these problems.
Now try adding and subtracting the following polynomials. Check your answers on pages 84-85.
16. Add 7x + 5 and 2x - 4.
17. Add 5a3 + 8a2 - 6 and 2a3 + 2a2 + 6.
18. (3x4 - 4x2 + 12) + (x4 + 5x2 + 2) =
19. Subtract a2 - 6a + 9 from 7a2 - 2a + 8.
20. (x2 - 5x + 8) - (7x2 + 5x + 2) =
Multiplying Exponential Terms
This hour began with the following example: x · x · x = x3.
It shows both the expanded form and the exponential form of “x to the third power.” Perhaps because exponents are a shortcut way to show multiplication of a base term, learning how to multiply monomials is actually easier than the adding and subtracting section you just completed.
Consider this multiplication problem:
x2 · x3
If you expand each of the terms, it becomes x2 · x3 = x · x · x · x · x, which equals x5.
To multiply a4 · a3, expanding each term results in a · a · a · a · a · a · a, which equals a7.
After a few of these examples, you surely can see the general rule for multiplying terms that have the same base: you simply keep the base and add the exponents.
Does this work for several monomials? Yes, if the bases are the same.
The following examples show how this rule is applied. The expanded form is shown here as explanation, but it is not needed. Notice also that the coefficients of the monomials are multiplied.
TIME SAVER
The exponential form shown for examples A through F helps you see how each of the monomials can be written as factors, but you should be able to give the answer without showing this step.
a. b5 · b2 = b · b · b · b · b · b · b = b7
b. (2x2)(5x4) = 2 · x · x · 5 · x · x · x · x = 10x6
c. (4a3)(-6a) = 4 · a · a · a · - 6 · a = -24a4
d. (-5x2y)(2xy3)(xy) = -5 · x · x · y · 2 · x · y · y · y · x · y = -10x4y5
e. 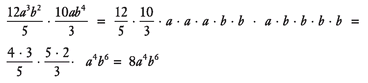
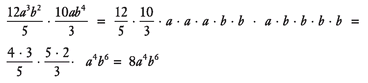
f. (2xy2)(5xy3) + (6y4)(x2y) = 2 · x · y · y · 5 · x · y · y · y + 6 · y · y · y · y · x · x · y = 10x2y5 + 6x2y5 = 16x2y5
Look again at examples B through F, and try to skip the expansion step to get from the problem directly to the solution by simply adding the exponents of the equal bases. Now that you have seen the detailed work on these problems, your goal should be to accurately move from the problem to the solution without expanding the terms with exponents, by adding the exponents instead.
As you reach the end of this hour on exponents, the final section explains how to simplify terms with exponents that are raised to another exponent. Expanding the terms, though, shows that the process is surprisingly easy to learn, and you’ll probably see a shortcut.
PROCEED WITH CAUTION
The parentheses in these “power” problems show that the factors inside will be multiplied times themselves, so they are important to each of the problems and are not just for emphasis.
Simplify: (x3)2
This problem could be described as “x to the third power, raised to the second power” or “x to the third, times itself.” To simplify it, expand it to see the exponents in clearer form:
(x3)2 = (x3) · (x3) = x · x · x · x · x · x = x6
Simplify: (2b2)3
This could be described as “2 b squared, raised to the third power.” Expand it to see the factors more clearly:
(2b 2)3 = (2b 2) (2b 2) (2b 2) = 2 · b · b · 2 · b · b · 2 · b · b = 8b6
The parentheses continue to play a very important role, so pay attention to what is inside them. Numbers or variables outside the parentheses are not affected by the exponent, but numbers or variables inside are affected, as you see in the following examples:
Simplify: 5x( y4)2
Solution: 5x( y4)2 = 5x · y4 · y4 = 5x · y · y · y · y · y · y · y · y = 5xy8
Simplify: (5xy4)2
Solution: (5xy4)2= 5xy4 · 5xy4 = 5 · 5 · x · x · y · y · y · y · y · y · y · y = 25x2y8
Simplify: - 6(a4 b3)2
Solution: -6(a4b3)2 = -6 ·a4b3·a4b3 = -6 · a · a · a · a · a · a · a · a · b · b · b · b · b · b = - 6a8 b6
Simplify: (-6a4b3)2 (Try to skip the expansion step.)
Solution: (- 6a4b3)2 = - 6a4b3 · - 6a4b3 = - 6 · - 6 · a4 · a4 · b3 · b3 = 36a8b6
TIME SAVER
The rule for raising a power to a power: multiply the powers.
Now try simplifying the following polynomials. Check your answers on page 85.
21. a4 · a5 =
22. (-3c3)(6c2) =
23. (2x3y2)(-3xy)(-2xy4) =
24. (3a2b3)(4ab2) + (2b4)(a3b) =
25. (a4)5 =
26. (4a3b4)2 =
27. 4(a3b4)2 =
Answers to Sample Problems
1. 94
2. -6 · c · d · d · d · d
3. 53x2y
4. -9ab2
5. 2 · 16 = 32
6. (8)2 = 64
7. 2 + 16 = 18
8. 62 = 36
9. -5 + -2 · -2 · -2 = -5 + -8 = -13
10. (2 + 4)2 -22 + 42 = (6)2 - 4 +16 = 36 - 4 + 16 = 32 + 16 = 48
11. 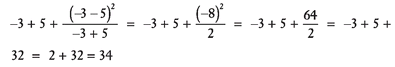
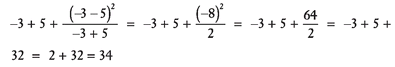
12. 5x4 - x3 + 4
13. -3a 2 + 8b3 - 4
14. 6y + 3y2 +5z
15. 3x3
16. 7x + 5 + 2x - 4 = 9x + 1
17. 5a3 + 8a2 - 6 + 2a3 + 2a2 + 6 = 7a 3 + 10a2
18. 4x4 + x2 + 14
19. 7a2 - 2a + 8 - (a2 - 6a + 9) = 7a2 - 2a + 8 - a2 + 6a - 9 = 6a2 + 4a - 1
20. (x2 - 5x + 8) - (7x2 + 5x + 2) - x2 - 5x + 8 - 7x2 - 5x - 2 = -6x2 - 10x + 6
21. a9
22. -18c5
23. 12x5y7
24. (3a2b3)(4ab2) + (2b4)(a3b) = 12a3b5 + 2a3b5 = 14a3b5
25. a20
26. 16a6b8
27. 4a6 b8
Review
Hour’s Up!
Based on what you’ve learned in Hour 7, do the following problems. Check your answers with the solution key in Appendix B.
1. Simplify: 4 · 32 =
a. 144
b. 49
c. 12
d. 36
2. Simplify: (4 · 3)2=
a. 144
b. 49
c. 13
d. 36
3. Simplify: 4 + 32=
a. 49
b. 10
c. 13
d. 4
4. Simplify: (2a)3 =
a. 6a
b. 2a3
c. 6a3
d. 8a3
5. If x = -4 and y = 3, evaluate 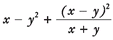 .
.
a. -62x y
b. 54
c. -44
d. -50
6. Simplify: 7a2b + 5b3 - 5a2b - 4 + 3b3 =
a. 12a2b + 8b3 - 4
b. 2a2b + 8b3 - 4
c. 2a2b + 2b3
d. 2a2b + 2b3 -4
7. Simplify: (8x4 - 3x2 + 9) + (x4 + 6x2 + 4) =
a. 9x8 + 3x4 + 13
b. 8x4+3x2 + 13
c. 9x4 + 3x2 + 13
d. 8x4 + 9x2 + 13
8. Simplify: (5a3 + 4a2 - 2a + 6) - (a3 + 6a 2 - 2a) =
a. 5a3 + 10a2 + 6
b. 4a3 - 2a2 + 6
c. 4a3 - 2a2 - 6
d. 5a3 - 2a2 + 6
9. Simplify: (2x3y)(4xy4) + (6y2)(x4y3) =
a. 48x8y10
b. 14x8y10
c. 14x4y5
d. 14x8y10
10. Simplify: (6a4b5)2 =
a. 36a8 b10
b. 12a6b7
c. 12a8 b10
d. 6a6b7
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.
