Hour 19
Solving Inequalities: Graphing
Learning how to solve systems of equations takes you into the two-dimensional world of ordered pairs and graphed lines with slopes and y-intercepts. The choices of how you find the solution for a system put you in charge, giving you the power to make a decision based on analyzing your options.
This hour, you return to solving problems with just one variable, but it’s not really a step backward. It’s taking the basic properties that help you solve equations and applying these same properties to solve problems you were introduced to in Hour 2—inequalities.
Solving and Graphing Inequalities
Many situations in life require an exact answer, including “How much acid should I add to 30 liters of 20% acidic solution to make it 40% acidic?” At other times, knowing a range of answers is more helpful, such as “What’s the least amount of money I must deposit to be sure my checking account isn’t overdrawn?”
In the acid solution example, setting up and solving an equation helps you find the answer. An equation always has an equals sign. If there is a variable in the equation, your job is to find the value of the variable that makes the equation true.
GO TO ◀
The acid solution problem is solved as an example in Hour 14.
In the checking account example, setting up and solving an inequality is the key. An inequality can have any of the following signs:
<, ≤, >, ≥
If there is a variable in the inequality, your job is to find the value(s) of the variable that make(s) the inequality true.
Fortunately, solving inequalities is similar to solving equations. Many of the same properties are used, with just a few variations that are not difficult to master.
Let’s begin by reviewing the four inequality symbols, shown here in word and symbol examples: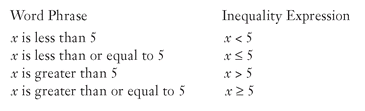
JUST A MINUTE
An easy way to remember < means “less than” is to notice that < looks like an L and “less than” begins with an L.
When you saw these symbols in Hour 2, they appeared in expressions like the following:
2 > -3 Is this a true statement? (yes)
3 ≥ 3 Is this a true statement? (yes)
-4 > 4 Is this a true statement? (no)
3 ≥ 3 Is this a true statement? (yes)
-4 > 4 Is this a true statement? (no)
These inequalities can be visualized and better understood when they are graphed on a number line:
JUST A MINUTE
The real number line extends from negative infinity on the left side to positive infinity on the right side. Zero separates the positive and negative numbers, and zero is the same distance from -1 as it is from +1.
2 > -3 is true because 2 is to the right of -3.
3 ≥ 3 is true because “greater than OR equal to” allows the numbers to
be equal.
-4 > 4 is false because -4 is to the left of 4; therefore,
-4 < 4 is the true statement.
3 ≥ 3 is true because “greater than OR equal to” allows the numbers to
be equal.
-4 > 4 is false because -4 is to the left of 4; therefore,
-4 < 4 is the true statement.
Your introduction to equations in Hour 5 included three types of equations:
True → 2 + 3 = 5
False → 2 + 3 = 6
Open → x + 3 = 5 → Open equations can be true or false,
depending on what number is put in for the variable.
False → 2 + 3 = 6
Open → x + 3 = 5 → Open equations can be true or false,
depending on what number is put in for the variable.
Inequalities have similar types:
True → 2 + 3 ≤ 5
False → 2 + 3 < 5
Open → x + 3 < 5 → As with equations, an open inequality
might be true or false, depending on what number is put in for
the variable.
False → 2 + 3 < 5
Open → x + 3 < 5 → As with equations, an open inequality
might be true or false, depending on what number is put in for
the variable.
Let’s begin by considering more closely the example of the open inequality :
x + 3 < 5
If it were written as an open equation, it would be this:
x + 3 = 5
Solving it mentally is easy → x = 2.
The algebraic solution step involves the subtraction property:
JUST A MINUTE
The subtraction property lets you subtract the same amount from both sides of a true equation to create a new equation that is also true.
x + 3 - 3 = 5 - 3
x = 2
x = 2
To check, put 2 in for x in the original equation:
2 + 3 = 5 → 5 = 5; therefore, x = 2 is the solution.
Solving the inequality relies on the same subtraction property:
x + 3 < 5
x + 3 - 3 < 5 - 3
x < 2
x + 3 - 3 < 5 - 3
x < 2
To check, put a number that is less than 2 in for x in the original equation:
1 + 3 < 5 → 4 < 5; therefore, x < 2 is the solution.
The subtraction property seems to apply to solving equations and inequalities. What if the inequality symbol is reversed? Try solving x + 3 > 5 with the subtraction property:
x + 3 > 5
x + 3 - 3 > 5 - 3
x > 2
x + 3 - 3 > 5 - 3
x > 2
To check, put a number greater than 2 in for x in the original equation:
3 + 3 > 5 → 6 > 5; therefore, x > 2 is the solution.
Yes, the subtraction property does apply to solving equations and inequalities.
Consider another open inequality:
x - 3 > 5
If it were written as an open equation, it would be this:
x - 3 = 5
Solving it mentally is easy → x = 8.
The algebraic solution step involves the addition property:
x - 3 = 5
x - 3 + 3 = 5 + 3
x = 8
x - 3 + 3 = 5 + 3
x = 8
JUST A MINUTE
The addition property lets you add the same amount to both sides of a true equation to create a new equation that is also true.
To check, put 8 in for x in the original equation:
8 - 3 = 5 → 5 = 5; therefore, x = 8 is the solution.
Solving the inequality relies on the same addition property:
x - 3 > 5
x - 3 + 3 > 5 + 3
x > 8
x - 3 + 3 > 5 + 3
x > 8
To check, put a number that is greater than 8 in for x in the original equation:
9 - 3 > 5 → 6 > 5; therefore, x > 8 is the solution.
The addition property applies to solving equations and inequalities.
A logical question at this point is how you know what number to put in for the variable when you check the inequality solution. The solution to the last inequality was x > 8, and 9 was chosen as the number. Would 10 have worked, or 11.8?
Yes, 10 - 3 > 5 and 11.8 - 3 > 5. When the solution is an inequality, such as x > 8, any number that is greater than 8 will be a solution. Looking at the graph for this solution may help you see this more clearly:
The solution is “all the numbers that are greater than 8.” An open circle on the +8 shows that you are not including 8 in the solution. The arrow to the right shows all those numbers—integers, fractions, decimals—that are to the right of 8. You can choose any of those numbers to put in the inequality for x, and each one will give a true inequality.

In the same way that equations like x + y = 6 create a line with an infinite number of solutions on the (x,y) graph in Hour 15, inequality solutions create a line or ray on the real number line and show an infinite number of solutions.
Equation solutions can also be graphed on a number line. You know that the solution to the equation x - 3 = 5 is x = 8. Its graph is a single point—+8 on the number line: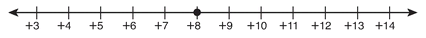
A final example of an inequality that is solved with the addition property includes the ≤ symbol:
Solve: x - 3 ≤ 4
Solution: Adding 3 to both sides isolates the x.
x - 3 ≤ 4
x - 3 + 3 ≤ 4 + 3
x ≤ 7
Solution: Adding 3 to both sides isolates the x.
x - 3 ≤ 4
x - 3 + 3 ≤ 4 + 3
x ≤ 7
To check, put a number less than or equal to 7 into the original inequality for x. 7 is less than OR equal to 7, so use 7:
7 - 3 ≤ 4 → 4 ≤ 4 True: 4 is less than OR equal to 4.
TIME SAVER
The number you choose to check your solution can be any number in the inequality: to check if x > 8 is the solution, choose 10 as the number to put in for x—it’s greater than 8 and probably easier to work with than 9 is.
Now try 6, because 6 is less than or equal to 7:
6 - 3 ≤ 4 → 3 ≤ 4 True: 3 is less than or equal to 4.
Graph this solution to see the answer more easily: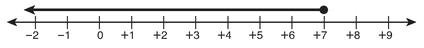
The graph is a line that begins solidly at +7 and goes to the left, because it includes all the numbers less than or equal to 7. The numbers on this solution line include all the integers, fractions, and decimals from 7 to negative infinity.
Now try to solve the following inequalities. Graph the solution on the number line, and check your answers on page 271.
1. x + 5 < 7
2. x - 3 ≥ -7
The inequalities you solved so far have used the addition and subtraction properties. Before you work on solving inequalities that include multiplying or dividing, look at the following basic inequalities.
Consider the true inequality:
6 < 12 → It is true that 6 is less than 12.
What if you multiply both sides by 3?
6 · 3 < 12 · 3 → 18 < 36 → True
What if you divide both sides by 3?
6 ÷ 3 < 12 ÷ 3 → 2 < 4 → True
Multiplying or dividing both sides of this true inequality by positive 3 makes new inequalities that are still true.
JUST A MINUTE

The ordering of negative numbers can be confusing: recall that -2 < -1 and -10 > -20. Putting these numbers on a number line may help because numbers are always increasing as you move to the right along the number line and decreasing as you move to the left.
What if you multiply both sides by -3?
6 · -3 < 12 · -3 → -18 < -36 → False!
Dividing both sides by -3:
6 ÷ -3 < 12 ÷ -3 → -2 < -4 → False!
When you multiply or divide an inequality by a negative number, the inequality must be reversed to make it true.
Begin again with 6 < 12.
You can multiply both sides by -3, but you must switch the inequality. “Less than” becomes “greater than,” as follows:
6 < 12 → True
6 · -3 > 12 · -3 → -18 > -36 → True
6 · -3 > 12 · -3 → -18 > -36 → True
The < reversed to > to make a true inequality.
You can also divide both sides by -3, as long as you switch the inequality:
6 < 12 → True
6 ÷ -3 > 12 ÷ -3 → -2 > -4 → True
6 ÷ -3 > 12 ÷ -3 → -2 > -4 → True
The < reversed to > to make a true inequality.
This rule is very important in specific situations. If you are solving an inequality and either multiply or divide both sides to isolate a variable, you must watch for this reversal process.
You must switch the inequality symbol if you multiply or divide by a negative number.
The inequality symbol stays the same for all adding and subtracting, and for all multiplying or dividing by a positive number.
Let’s consider an inequality that involves multiplication:
5x < 10
You can easily solve this with mental math: x < 2
The algebraic solution step uses the division property:
5x < 10
5x ÷ 5 < 10 ÷ 5
x < 2
5x ÷ 5 < 10 ÷ 5
x < 2
JUST A MINUTE
The division property lets you divide both sides of a true equation by the same number to create a new equation that is also true. It also applies to inequalities, as long as the number you divide by is positive.
To check, put a number less than 2 in for x in the original inequality. Use 1:
5 · 1 < 10 → 5 < 10; therefore, x < 2 is the solution.
Notice that you divided by positive 5, so the < symbol stayed the same.
Follow the solution steps for the following inequality:
-3x < 18
Don’t try solving this mentally, because the -3 needs to be divided on both sides, and the inequality must switch.
-3x < 18
-3x ÷ -3 > 18 ÷ -3 Dividing by -3: switch to >
x > -6
-3x ÷ -3 > 18 ÷ -3 Dividing by -3: switch to >
x > -6
To check, put a number greater than -6 into the original inequality for x. Use -5:
-3 · -5 < 18 → 15 < 18 → True
Therefore, x > -6 is the solution. It’s important that you switch the inequality symbol only as you work to isolate the variable. The original inequality doesn’t change. It can be difficult to keep track of these signs. Fortunately, it occurs only in the limited situation of multiplying or dividing by a negative number, but you must be aware of the importance of the effect.
The following inequality includes two operations, and the solution steps follow:
(The inequality didn’t switch—you didn’t divide by a negative number.)
2x - 8 ≥ -14
Solution: Your goal is to isolate the variable. Move the 8 by adding 8 to both sides, and then move the 2.
2x - 8 + 8 ≥ -14 + 8
2x ≥ -6
2x ÷ 2 ≥ -6 ÷ 2
x ≥ -3
2x ≥ -6
2x ÷ 2 ≥ -6 ÷ 2
x ≥ -3
To check, put a number greater than or equal to -3 into the original inequality for x. Use 0:
2 · 0 - 8 ≥ -14 → 0 - 8 ≥ -14 → -8 ≥ -14 → True
Therefore, x ≥ -3 is the solution.
Now try to solve the following inequalities. Graph the solutions on the following number lines, and check your answers on pages 271-272.
3. 6x - 3 < 21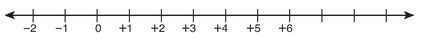
4. -3x + 7 ≤ 25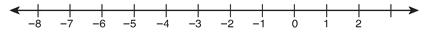
5. 9 + 2x > -11
The solutions to all the inequalities so far have been graphed lines that go to either positive or negative infinity from a specific beginning point. They give a visual picture of inequalities like x < 5, a very efficient way to say “all the numbers less than 5.”
Sometimes you need to refer to a range of numbers. If you suspect you have a fever, you probably don’t need to be concerned if your temperature is between 97.5° and 100.5°. You might need to see a doctor if it’s above or below that range. The “safe range” can best be expressed with a new type of inequality, as you’ll see in the next section.
Solving and Graphing Combined Inequalities
Describing a variable as having a value between two numbers can most efficiently be written as an interval, with inequality symbols setting the boundaries. The example of a non-emergency body temperature range is shown with the following statements and inequalities:
acceptable for your temperature to be above 97.5” can be written like this:
t > 97.5; this can be reversed and be written 97.5 < t.
PROCEED WITH CAUTION
The direction of an inequality reverses when the sides are reversed: 2 < 10 → 10 > 2; x < 3 → 3 > x.
“It is acceptable for your temperature to be below 100.5” can be written like this:
t < 100.5
When you combine these inequalities, the result is this:
97.5 < t < 100.5
In this combined form, the variable—your temperature—can be between 97.5° and 100.5°.
Graphing this interval makes it clear that t is between the two numbers on the graph, as well as in the combined inequality:

In the temperature example, the solution is the interval itself, because the t is already isolated.
Consider the following combined inequality:
8 ≤ x - 4 ≤ 15
To solve this interval, isolate the x by adding 4 to all three parts of the inequality:
8 + 4 ≤ x - 4 + 4 ≤ 15 + 4
12 ≤ x ≤ 19
12 ≤ x ≤ 19
To check, choose a number between 12 and 19 to put into the original inequality for x. Use 15:
8 ≤ 15 - 4 ≤ 15 → 8 ≤ 11 ≤ 15 → True
Therefore, 12 ≤ x ≤ 19 is the solution (all the numbers between 12 and 19, including 12 and 19).
The graph follows:

As with simpler inequalities, multiplying or dividing by a negative number reverses the inequality symbols:
-6 < -2x + 4 < 16
Solution: Isolate the variable by subtracting 4 from all three parts, and then divide all three results by -2.
-6 < -2x + 4 < 16
-6 - 4 < -2x + 4 - 4 < 16 - 4
-10 < -2x < 12
-10 ÷ -2 > -2x ÷ -2 > 12 ÷ -2
5 > x > -6
-6 - 4 < -2x + 4 - 4 < 16 - 4
-10 < -2x < 12
-10 ÷ -2 > -2x ÷ -2 > 12 ÷ -2
5 > x > -6
The preferred order for these interval solutions is to have the smaller number on the left side and the larger on the right—the same way the number line is displayed. So each of the terms can be reversed as long as each inequality symbol is also reversed:
-6 < x < 5
The solution: “all numbers between -6 and 5”
In this problem, the inequality symbols were reversed because of the division by -2, and then they were reversed again to put the smaller number on the left side of the expression. You have lots to keep track of here, but the process is always consistent, which is one of the certainties of algebra.
Now try to solve these combined inequalities, graphing the solutions and checking your answers on page 272.
6. -4 ≤ 2x + 6 ≤ 10
7. -6 ≤ -3x - 9 ≤ 12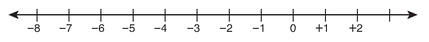
Answers to Sample Problems
1. x + 5 - 5 < 7 - 5 → x < 2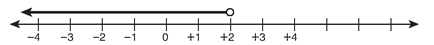
2. x - 3 + 3 ≥ -7 + 3 → x ≥ -4

3. 6x - 3 + 3 < 21 + 3 → 6x < 24 → 6x ÷ 6 < 24 ÷ 6 → x < 4
4. -3x + 7 - 7 ≤ 25 - 7 → -3x ≤ 18 → -3x ÷ -3 ≥ 18 ÷ -3 → x ≥ -6
5. 9 + 2x - 9 > -11 - 9 → 2x > -20 → 2x ÷ 2 > -20 ÷ 2 → x > -10
6.
-4 ≤ 2x + 6 ≤ 10
-4 - 6 ≤ 2x + 6 - 6 ≤ 10 - 6
-10 ≤ 2x ≤ 4
-10 ÷ 2 ≤ 2x ÷ 2 ≤ 4 ÷ 2
-5 ≤ x ≤ 2
-4 - 6 ≤ 2x + 6 - 6 ≤ 10 - 6
-10 ≤ 2x ≤ 4
-10 ÷ 2 ≤ 2x ÷ 2 ≤ 4 ÷ 2
-5 ≤ x ≤ 2
7. 
-6 ≤ -3x - 9 ≤ 12
-6 + 9 ≤ -3x - 9 + 9 ≤ 12 + 9
3 ≤ -3x ≤ 21
3 ÷ -3 ≥ -3x ÷ -3 ≥ 21 ÷ -3
-1 ≥ x ≥ -7 (Reverse all terms and symbols.)
-7 ≤ x ≤ -1
-6 + 9 ≤ -3x - 9 + 9 ≤ 12 + 9
3 ≤ -3x ≤ 21
3 ÷ -3 ≥ -3x ÷ -3 ≥ 21 ÷ -3
-1 ≥ x ≥ -7 (Reverse all terms and symbols.)
-7 ≤ x ≤ -1

Review
Hour’s Up!
Based on what you’ve learned in Hour 19, find the solutions for the following inequalities. Check your answers with the solution key in Appendix B.
1. x - 5 > 3
a. x > 8
b. x < 8
c. x > -8
d. x < -8
2. x + 3 ≤ 9
a. x ≥ -6
b. x ≥ 6
c. x ≤ -6
d. x ≤ 6
3. 2x ≥ -10
a. x ≤ 5
b. x ≤ -5
c. x ≥ -5
d. x ≥ 5
4. 3x - 8 ≤ 4
a. x ≤ 4
b. x ≤ -4
c. x ≥ 4
d. x ≥ -4
5. -5x > 10
a. x < 2
b. x < -2
c. x > -2
d. x > 2
6. -2x + 6 ≤ 14
a. x ≥ -4
b. x ≥ 4
c. x ≤ -4
d. x ≤ 4
7. -3x - 2 ≤ 13
a. x ≤ 5
b. x ≤ -5
c. x ≥ -5
d. x ≥ 5
8. 7 + 2x > 9
a. x < 1
b. x < -1
c. x > -1
d. x > 1
9. 3 - 2x > 11
a. x < 4
b. x < -4
c. x > -4
d. x > 4
10. 4x + 1 ≤ -19
a. x ≤ -5
b. x ≤ 5
c. x ≥ 5
d. x ≥ -5
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.
