Hour 8
Polynomials: Solving Equations and Multiplying
The exponents that you learned about in the previous hour are powerful—no pun intended—and they allow you to work with algebra problems that are quite complex. Don’t forget that they are efficient, as they help make lengthy multiplication expressions very compact.
You can now add and subtract polynomials that include exponents. You can also multiply monomials to get a simplified answer and raise monomials to powers. In this hour, you learn about multiplying polynomials by monomials and by other polynomials, and how polynomials can be used to solve word problems. First, let’s combine your knowledge of polynomials with basic equation skills to solve some new equations.
Solving Equations That Include Polynomial Terms
Look at the following equation that includes a difference of two binomials:
a. (3x + 4) - (x + 1) = 13
To solve it, simplify the left side by subtracting the binomials and then isolate the variable.
JUST A MINUTE
Subtraction can be changed to addition if you change the sign of the terms after the subtraction sign. For example, 2 - 6 = 2 + -6 = -4 and 9 - (x + 5) = 9 + - x + -5 = 4 - x.
Solve: (3x + 4) - (x + 1) = 13
3x + 4 + -x + -1 = 13
3x + -x + 4 + -1 = 13
2x + 3 = 13
2x + 3 - 3 = 13 - 3
2x = 10
2x ÷ 2 = 10 ÷ 2
x = 5
3x + -x + 4 + -1 = 13
2x + 3 = 13
2x + 3 - 3 = 13 - 3
2x = 10
2x ÷ 2 = 10 ÷ 2
x = 5
To check, put 5 in for x in the original equation:
(3 · 5 + 4) - (5 + 1) = 13 → 3 · 5 + 4 - (6) = 13 → 15 + 4 - 6 = 13
→ 19 - 6 = 13 → 13 = 13. Therefore, x = 5 is the solution.
→ 19 - 6 = 13 → 13 = 13. Therefore, x = 5 is the solution.
With your ability to simplify polynomials that are added or subtracted, you can solve equations that contain these expressions. They just need to be simplified to become the same types of equations you learned how to solve in Hours 5 and 6.
Now try to solve the following equations, and check your answers on page 96.
1. (5a + 6) + (2a - 7) = 6
2. 12x + (6 - 2x) = 4(x - 3)
3. 2(a + 4) - 5(a + 1) = 15
4. (b - 8) + (3b + 7) = (b - 3) + (b + 12)
Solving Word Problems with Basic Polynomial Equations
Polynomials appear in many different kinds of word problems that can be written as equations and then solved. Some, such as problems about consecutive integers, are totally based on algebra. Others, like distance problems, come from more practical situations. As in Hours 1 and 6, the first step is to change the word problem into an algebraic equation. Reading each problem carefully will help you decide what the variable is and what operation is needed.
JUST A MINUTE
Remember that consecutive integers are next to each other on the number line. Given any integer, add 1 to find the consecutive integer. For example, 6 and 7 are consecutive integers, as are -10 and -9. If the variable x is an integer, the consecutive integer is x + 1.
Consider the following problem about consecutive integers:
b. What two consecutive integers have a sum of 47?
Solution: Begin by writing an equation that describes the problem. Let x be the first integer, so x + 1 is the consecutive integer. Write and solve the equation:
x + (x + 1) = 47
2x + 1 = 47
2x + 1 - 1 = 47 - 1
2x = 46
2x ÷ 2 = 46 ÷ 2
x = 23
2x + 1 = 47
2x + 1 - 1 = 47 - 1
2x = 46
2x ÷ 2 = 46 ÷ 2
x = 23
To check, put x = 23 into the original equation:
23 + (23 + 1) = 47 → 23 + 24 = 47 → 47 = 47
Therefore, x = 23 is the solution. The question asks for two consecutive integers, and they are 23 and 24.
The next two problems have operations that are slightly more complex:
c. The greater of two consecutive integers is 15 less than twice the smaller integer. What are the integers?
Solution: Let x and x + 1 be the consecutive integers, as in the previous problem. To write the equation, you need to know which is the greater, x or x + 1. Adding 1 to a number always gives a number that’s greater, so x + 1 is the greater integer. Begin with x + 1 as you change the written problem into an equation. “Less than” indicates subtraction, so be careful to put the terms in the correct order. Write and solve the equation:
x + 1 = 2x - 15
x + 1 - x = 2x - 15 - x
1 = x - 15
1 + 15 = x - 15 + 15
16 = x or x = 16
x + 1 - x = 2x - 15 - x
1 = x - 15
1 + 15 = x - 15 + 15
16 = x or x = 16
To check, put x = 16 into the original equation:
16 + 1 = 2 · 16 - 15 → 17 = 32 - 15 → 17 = 17
Therefore, x = 16 is the solution. The integers are 16 and 17.
As with the prior problem, the next one includes more complex operations.
d. Twice the greater of two consecutive integers is 7 less than three times the smaller integer. What are the integers?
Solution: Again, x and x + 1 will represent the consecutive integers, with x + 1 being the greater one. Translate the words of the problem into an equation and solve it. “Twice” means multiplying by 2, so the first part of the problem is written as 2(x + 1). “7 less than three times the smaller integer” is written as 3x - 7. (Remember that subtraction is the “less than” operation, and the order is important in subtraction.) Figure out these algebraic phrases together to write your equation, as shown here.
2(x + 1) = 3x - 7
2x + 2 = 3x - 7
2x + 2 - 2x = 3x - 7 - 2x
2 = x - 7
2 + 7 = x - 7 + 7
9 = x or x = 9
2x + 2 = 3x - 7
2x + 2 - 2x = 3x - 7 - 2x
2 = x - 7
2 + 7 = x - 7 + 7
9 = x or x = 9
To check, put x = 9 into the original equation:
2(9 + 1) = 3 · 9 - 7 → 2 · 10 = 27 - 7 → 20 = 20
Therefore, x = 9 is the solution, and the two consecutive integers are 9 and 10.
Now try to solve the following word problems, and check your answers on page 96.
5. What two consecutive integers have a sum of 37?
6. Three times the greater of two consecutive integers is 5 less than four times the smaller integer. What are the integers?
These consecutive integer word problems bring together basic monomials, such as x and 3x, and basic polynomials, such as 2x + 2, creating equations that can be solved. The rest of this hour, you learn how to multiply and simplify more complex monomials and polynomials, using the distributive property from Hour 4 and your knowledge of exponents from Hour 7.
Multiplying Monomials and Polynomials
The distributive property allows you to simplify expressions that have a binomial multiplied by a number. To put it more plainly, you know that, to simplify 3(x + 7), you multiply 3 times x and 3 times 7. The answer, 3x + 21, is called “simplified” because the answer has no parentheses and is now a simple binomial. This same property works when monomials and polynomials are multiplied, as in the following examples.
JUST A MINUTE
The distributive property says that when you multiply a sum by a number, it is the same as adding the product of the numbers. For example, a · (b + c) = (a · b) + (a · c).
e. Simplify: a(a + 8)
Solution: Multiply a times each term inside the parentheses.
a(a + 8) = a2 + 8a
To multiply terms that have the same base, keep the base and add the exponents. For example, (x2)(x3) = x2 + 3 = x5. If a factor has a coefficient, multiply the coefficients of each factor. For example, (3x)(4x) = 12x2. Terms that show no coefficient have a coefficient of 1. The following examples show how to work with the distributive property that includes terms with exponents.
f. Simplify: 6x(2x2 + 3x - 4)
Solution: The distributive property is not limited to binomials. Any number of terms can be included within the parentheses. To simplify, multiply 6x times each of the trinomial’s terms, following the rules for exponents that you learned in Hour 7:
6x(2x2 + 3x - 4) =
6x ·2x2 + 6x·3x + 6x· -4
12x3 + 18x2 - 24x
6x ·2x2 + 6x·3x + 6x· -4
12x3 + 18x2 - 24x
g. Simplify: -3a2b(2a3 + 5a2b2 - 3b3)
Solution: To simplify, multiply -3a2b times each of the trinomial’s terms. Watch the signs very carefully!
-3a2b(2a3 + 5a2b2 - 3b3) =
-3a2b · 2a3 -3a2b · 5a2b2 - 3a2b · -3b3 =
- 6a5b - 15a4 b3 + 9a2b4
-3a2b · 2a3 -3a2b · 5a2b2 - 3a2b · -3b3 =
- 6a5b - 15a4 b3 + 9a2b4
Now try these problems, using the distributive property, order of operations, and exponent rules to combine the like terms, as needed. Check your answers on page 96.
7. 5x(2x2 + 3x -5) =
8. -2a4(3a2 - 2a +6)=
9. 3x(x2 +4x -1) + 4x(2x2 + 5x + 4) =
10. a2(3a - 4) - a(2a2 + 5a) =
As you have seen throughout this hour, the process of multiplying monomials times other polynomials brings together several different algebraic skills. It is a perfect example of what you may have heard about algebra: each new concept builds on the previous one. This logical progression leads to looking at what happens when you multiply by a binomial instead of a monomial.
Multiplying Polynomials
Now that you can multiply by monomials, let’s push the distributive property to the next level and learn how to multiply by a binomial expression.
You know how to do the following multiplication problem, but look closely at the solution steps:
x(x2 + 3) = x · x2 + x · 3 = x3 + 3x
Using the distributive property, you multiply the x in front of the parentheses times each of the terms inside the parentheses—x2 + 3—as your first step and then simplify the terms to get the answer.
Now change the x in front of the parentheses to (x + 2).
The new problem is:
(x + 2)(x2 + 3)
To simplify it, follow the same process. Multiply (x + 2) times each of the terms inside the parentheses as your first step. Then simplify to get the answer. The steps look like this:
(x + 2)(x2 + 3)
(x + 2) · x2 + (x + 2) · 3 =
x3 + 2x2 + 3x + 6
(x + 2) · x2 + (x + 2) · 3 =
x3 + 2x2 + 3x + 6
JUST A MINUTE
The distributive property applies when the terms are reversed: (b + c) · a = a · b + a · c
Be sure to check for like terms to see if more work is needed. There are no like terms, so this is the final answer.
You can always use the distributive property to simplify polynomial multiplication problems like this one, but there’s a shortcut that is a little easier. Look at how the same problem can be done with another method:
(x + 2)(x2 + 3) =
x · x2 + x · 3 + 2 · x2 + 2 · 3 =
x3 + 3x + 2x2 + 6
x · x2 + x · 3 + 2 · x2 + 2 · 3 =
x3 + 3x + 2x2 + 6
Comparing this answer to the previous one, you see that they are the same; the terms of a polynomial can be written in any order. Usually the answer is shown in descending order, with the highest exponent first, but this is not required.
This shortcut method can be described as follows:
Multiply each of the terms in the first set of parentheses times each term in the second set. This will have the same effect as applying the distributive property, but it’s easier to remember and seems easier than going through the distributive process. You are free to use either method.
This multiplication process can be used for more than just binomials, as you see in the next example of multiplying a binomial times a trinomial:
(x + 5)(x2 + 4x - 6) =
x · x2 + x · 4x + x · -6 + 5 · x2 + 5 · 4x + 5 · -6 =
x3 + 4x2 - 6x + 5x2 + 20x - 30 =
x3 + 9x2 + 14x - 30
x · x2 + x · 4x + x · -6 + 5 · x2 + 5 · 4x + 5 · -6 =
x3 + 4x2 - 6x + 5x2 + 20x - 30 =
x3 + 9x2 + 14x - 30
PROCEED WITH CAUTION
Be careful to combine only like terms, which are those with exactly the same variables and exactly the same exponents. When adding and subtracting terms, the exponents can never change—only the coefficients will change.
You do not need to write the step after the first equals sign. It is shown here to help you see the process at work. You should be able to omit that line of work and go directly to the line that begins with x3 + 4x2 - 6x …. Be sure that you watch the signs in the polynomial terms and combine all the like terms to get the final answer in simplest form.
Now try these multiplication problems, writing your final answer in simplest form. Check your answers on pages 96-97.
11. (x + 3)(x + 5) =
12. (x + 2)(x2 + 3x - 4) =
Multiplying two binomials is the most common type of polynomial multiplication in algebra, so let’s finish the hour learning an efficient method.
Multiplying Two Binomials
When you worked on problem 11 in the previous section, you probably multiplied x times x + 5 and 3 times x + 5, and then combined the like terms. There’s an even shorter way to multiply two simple binomials like these. See it develop as you look at two more examples of binomial multiplication:
and
(x + 4)(x + 6) =
x2 + 6x + 4x + 24 =
x2 + 10x + 24
x2 + 6x + 4x + 24 =
x2 + 10x + 24
(x + 3)(x + 7) =
x2 + 7x + 3x + 21 =
x2 + 10x + 21
x2 + 7x + 3x + 21 =
x2 + 10x + 21
The basic idea for the shortcut is to give special labels to the terms in each binomial based on its location in the problem. Using (x + 2)(x + 4) as the example, label the terms as follows:

This is called the FOIL method, based on the first letters of the identified terms—First, Outside, Inside, Last. It also works if any of the terms are negative. You just need to pay close attention to the signs. After you FOIL a few problems, you will see how efficient it is.
JUST A MINUTE
Remember that subtracting is the same as adding the opposite: x - 4 = x + (-4).
Follow the FOIL steps for (x + 6)(x + 3), shown here on one line:
(x + 6)(x + 3) → First: x2 Outside: + 3x Inside: + 6x Last: + 18
Combining all the terms, you get → x2+ 9x + 18.
The following example includes a negative term:
(x - 4)(x + 5) → First: x2 Outside: + 5x Inside: -4x Last: -20
Combining all the terms, you get → x2 + x - 20.
This final example shows the unique case of the disappearing x term:
(x + 6)(x - 6) → First: x2 Outside: - 6x Inside: + 6x Last: -36
Combining all the terms, you get → x2 - 36. (Note: Because 6x and - 6x are opposites, the sum of these terms is 0x or just 0.)
You get this type of answer when the last terms in the binomials are opposites of each other, as in:
(x - 5)(x + 5) = x2 + 5x - 5x - 25 = x2 - 25
You can skip the middle step or show the work, as you prefer.
Now try these multiplication problems, using the FOIL method:
13. (x + 2)(x + 5) =
14. (x + 8)(x + 1) =
15. (x - 3)(x + 4) =
16. (x + 3)(x - 3) =
Check your answers on page 97.
Answers to Sample Problems
1. 7a - 1 = 6 → 7a - 1 + 1 = 6 + 1 → 7a = 7 → 7a ÷ 7 = 7 ÷ 7 → a = 1
2. 12x + 6 - 2x = 4x - 12 → 10x + 6 = 4x - 12 → 10x + 6 - 4x = 4x - 12 - 4x → 6x + 6 = -12 → 6x + 6 - 6 = -12 - 6 → 6x = -18 → 6x ÷ 6 = -18 ÷ 6 → x = -3
3. 2a + 8 - 5a - 5 = 15 → -3a + 3 = 15 → -3a + 3 - 3 = 15 - 3 → -3a = 12 → -3a ÷ -3 = 12 ÷ -3 → a = -4
4. 4b - 1 = 2b + 9 → 4b - 1 - 2b = 2b + 9 - 2b → 2b - 1 = 9 → 2b - 1 + 1 = 9 + 1 → 2b = 10 → 2b ÷ 2 = 10 ÷ 2 → b = 5
5. The equation is x + (x + 1) = 37 → 2x + 1 = 37 → 2x + 1 - 1 = 37 - 1 → 2x = 36 → 2x ÷ 2 = 36 ÷ 2 → x = 18. The two integers are 18 and 19.
6. The equation is 3 (x + 1) = 4x - 5 → 3x + 3 = 4x - 5 → 3x + 3 - 3x = 4x - 5 - 3x → 3 = x - 5 → 3 + 5 = x - 5 + 5 → 8 = x or x = 8. The two integers are 8 and 9.
7. 5x(2x2 + 3x - 5) = 10x3 + 15x2 - 25x
8. -2a 4(3a2 - 2a + 6) = -6a6 + 4a5 - 12a4
9. 3x(x2 + 4x - 1) + 4x(2x2 + 5x + 4) = 3x3 + 12x2 - 3x + 8x3 + 20x2 + 16x = 11x3 + 32x2 + 13x
10. a2(3a - 4) - a(2a + 5a) = 3a3 - 4a2 - 2a3 - 5a2 = a3 - 9a2
11. (x + 3)(x + 5) = x ·x + x · 5 + 3 · x + 3 · 5 x2 + 5x + 3x + 15 = x2 + 8x + 15
12. (x + 2)(x2 + 3x - 4) = x3 + 3x2 - 4x+ 2x2 + 6x - 8 = x3 + 5x2 + 2x - 8
13. (x + 2)(x + 5) = x2 + 5x + 2x + 10 = x2 + 7x + 10
14. (x + 8)(x + 1) = x2 + 1x + 8x + 8 = x 2 + 9x + 8
15. (x - 3)(x + 4) = x2 + 4x - 3x - 12 = x2 + x - 12
16. (x + 3)(x - 3) = x2 - 3x + 3x - 9 = x2 - 9
Review
Hour’s Up!
Based on what you’ve learned in Hour 8, do the following problems. Check your answers with the solution key in Appendix B.
1. Solve for x: 3(x - 4) - 4(x + 2) = 2(2x - 5)
a. 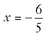
b. x = -1
c. x = -2
d. x = -3
2. Five times the greater of two consecutive integers is 4 less than six times the smaller integer. What are the integers?
a. 8 and 9
b. 9 and 10
c. 10 and 11
d. 6 and 7
3. Simplify: 4a(3a2 + 5a - 2) =
a. 12a3 + 9a2 - 8a
b. 12a3 + 20a2 - 6a
c. 12a3 + 9a2 + 8a
d. 12a3 + 20a2 - 8a
4. Simplify: -3x3(2x2 - 5x - 1) =
a. - 6x5 + 15x4 + 3x3
b. 6x5 - 15x4 + 3x3
c. - 6x5 + 15x4 - 3x3
d. -6x5 - 15x4 - 3x3
5. Simplify: x3 (2x - 5) + x(6x3 + x2) =
a. - 4x4 - 4x3
b. -8x4 - 4x3
c. 8x4 - 4x3
d. -8x4 + 4x3
6. Simplify: x3(2x - 5) - x(6x3 + x2) =
a. - 4x4 - 6x3
b. - 4x4 - 4x3
c. 2x4 - 11x3 + x2
d. - 6x4 - 4x3
7. Simplify: (x + 3)(x2 - 2x + 5) =
a. x3 + x2 + 11x + 15
b. x3 + x2 - x + 15
c. x3 - x2 - x - 15
d. x3 - x2 + 11x + 15
Use the FOIL method to simplify problems 8 through 10.
8. Simplify: (x + 3)(x + 4) =
a. x2 + 7x + 12
b. x2 + 12x + 7
c. x2 + 7x + 7
d. x2 + 12x + 12
9. Simplify: (x + 5)(x + 2) =
a. x2 + 10x + 10
b. x2 + 7x + 10
c. x2 + 7x + 7
d. x2 + 10x + 7
10. Simplify: (x - 7)(x + 7) =
a. x2 + 7x - 49
b. x2 - 7x + 49
c. x2 - 49
d. x2 + 49
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.
