Hour 16
Equations with Two Variables: Equations of Lines
Last hour’s graphing of points and lines from equations with an x and a y variable showed you one way to find many ordered pairs that are true for a given equation. Plotting the intercepts allowed you to draw the line that contains each equation’s solutions.
This hour you will learn how to use a line’s slope and key points to write that line’s equation—in some ways, the reverse of the process you learned last hour—along with how to solve real-life problems about direct and inverse variation.
Finding the Equation of a Line from the Slope and y-Intercept
The graph of the equation y - 2x = 6 follows. When x = 0, y = 6, and when y = 0, x = -3. These two key points are the ordered pairs (0,6) and (-3,0). (0,6) is the y-intercept, and (-3,0) is the x-intercept.
JUST A MINUTE
Ordered pairs are always written as (x,y) points and are graphed with the first number as x and the second number as y. The ordered pair (2,3) is graphed by moving two units to the right of (0,0) and then moving three units up.
The slope of this line is the ratio of rise to run → 6 to 3 → 2.
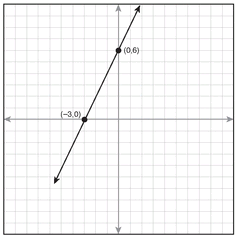
The preceding graph came from the equation y - 2x = 6.
If you move some of the terms and isolate the y variable, the equation would be this:
y - 2x = 6
y - 2x + 2x = 6 + 2x
y = 6 + 2x
y = 2x + 6
y - 2x + 2x = 6 + 2x
y = 6 + 2x
y = 2x + 6
JUST A MINUTE
To “isolate the variable y” is the same as to “solve the equation for y.” The y variable needs to be alone on the left side, and the x variable and the number, or constant, term need to be on the right side of the equals sign.
When the equation is written as y = 2x + 6, the 2 is the slope and the 6 is the y-intercept of the graph.
Looking at the intercepts and slope of the next two graphs might help you see this is not a coincidence—there’s definitely a close connection between the numbers in the equation and the slope and y-intercept:
line A: y = x + 3 line B: y = -2x + 6
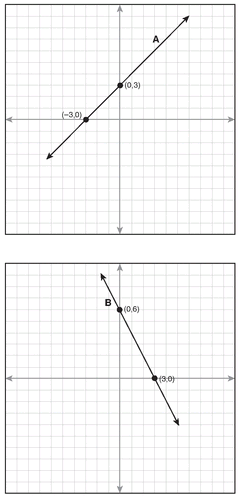
y-intercept: 3

Line A’s equation:
y = x + 3
y-intercept: 6
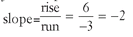
Line B’s equation:
y = -2x + 6
Did you notice that the slope and the y-intercept from each graph also appear in the equation? (The x-intercept is helpful for graphing, but it isn’t included in the equation.)
In each equation, the y is isolated on the left side of the equals sign. The x with its coefficient is on the right side, followed by a number, called a constant. The slope is the coefficient of the x term, and the y-intercept is the constant. This leads to the slope/intercept formula for the graph of a line:
y = mx + b, where m equals the slope of the line and b equals the y-intercept
The following graphs give additional examples of possible m and b values, as shown by the slope and y-intercepts of these lines:
line C: y = 3x - 1 line D: 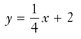


The key information you need from each graph is the slope of the line and the y-intercept—the x-intercept cannot be directly read from the equation of a line.
From the equation for line C, y = 3x - 1, you can see that m = 3 and b = -1. The graph of line C does have a y-intercept of -1 and a slope of 3.
From the equation for line D, 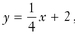 , you can see that
, you can see that  and b = 2. The graph of line D does have a y-intercept of 2 and a slope of
and b = 2. The graph of line D does have a y-intercept of 2 and a slope of  .
.
The important part of this connection between the line and the equation is that if you know the slope and y-intercept for any line, you can write the equation for that line.
You might know the line’s slope and y-intercept from examining the graph of the line, or you might simply be told what the slope and y-intercept are. Either way, the equation for the line is based on y = mx + b.
For example, the equation for the line with slope of 4 and y-intercept of -3 is:
y = 4x - 3
And the equation for the line with slope of 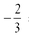 and y-intercept of
and y-intercept of 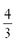 is:
is: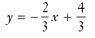 (This line would be rather difficult to graph, but it could be done.)
(This line would be rather difficult to graph, but it could be done.)
Now try to write the equation based on y = mx + b for each of the following lines, using their slope and y-intercept for m and b. Check your answers on pages 216-217.
1. 

Equation of line E:
2. 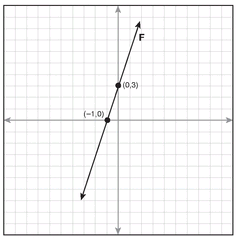

Equation of line F:
3. The slope of line G is -5, and the y-intercept is 8. Write the equation of line G.
The equation of a line can easily be written when you can find the slope and y-intercept from the graph or when you are told the values of the slope and y-intercept. Your algebra skills can also help you write the equation when the information you have is not quite so complete.
Finding the Equation of a Line from the Slope and a Point on the Line
If you know a line’s slope (m) and y-intercept (b), you can write its equation with the help of y = mx + b. However, if all you know is the slope of the line and a random point on that line, how do you know the b value and the y-intercept?
You have at least two choices:
1. Graph the line, using the point and the line’s slope.
2. Let algebra help you find the b value.
In the first choice, graphing is certainly possible, but it depends on your abilities with graph paper, straightedges, and so on. This could be challenging if the slope is a fraction or if the given point is something like (-8,28).
The second choice—using algebra to help you find the b value—makes perfect sense because you have been spending many hours learning algebra, and now it can be put to a good use. Let’s try it.
Consider the following information about a line:
The slope of the line is 3 and a point on the line is (4,6). What is its equation?
You know that your goal is to find the values of m and b for this line and then put these values into y = mx + b. You already know that m = 3.
You also know what x and y are: if the ordered pair (4,6) is on the line, then x = 4 and y = 6 in the equation y = mx + b. The process for finding the equation of this line follows:
Begin with y = mx + b.
Of these variables, you know from the point (4,6) that x is 4 and y is 6. You are also told that the slope is 3, so m is 3. Put these values in for y, m, and x:
y = mx + b
6 = 3 · 4 + b
6 = 3 · 4 + b
Solve this equation for b:
6 = 3 · 4 + b
6 = 12 + b
6 - 12 = 12 + b - 12
-6 = b
6 = 12 + b
6 - 12 = 12 + b - 12
-6 = b
You now know that b = -6. Put b = -6 along with m = 3 into y = mx + b, and you have the equation you are looking for:
y = 3x - 6
TIME SAVER
Graphing your equation is one way to check your work, but another, more efficient way, is to put the given point’s x and y values into your equation. Does 6 equal 3 · 4 - 6? Yes, so your equation is correct.
You could verify this by graphing this equation, and you would see that a line with y-intercept of -6 and slope of 3 does contain the point (4,6), but this verification isn’t necessary. Your algebra skills will serve you well in this and many other equation-writing problems.
Follow the solution steps on the next example. Find the equation for the line that goes through the point (1,4) and has a slope of -2.
In this problem, the ordered pair (1,4) tells you that x = 1 and y = 4. The slope is -2, so m = -2. You need to find the b value. Put the values you know into y = mx + b:
4 = -2 · 1 + b
4 = -2 + b
4 + 2 = -2 + b + 2
6 = b
4 = -2 + b
4 + 2 = -2 + b + 2
6 = b
Because m = -2 and b = 6, the equation for the line is y = -2x + 6.
Now try to write the equation for each of the following lines, checking your answers on page 217.
4. Find the equation of the line that has a slope of -8 contains the point (-3,2).
5. Find the equation of the line that contains the point (5,-6) and has a slope of -3.
When you know the point on a line and the line’s slope, substituting the values for x, y, and m into y = mx + b gives you a way to know what b equals, and that leads you directly to knowing the equation of the line.
You can now write the equation of a line from two different methods: analyzing its graph to find its slope and its y-intercept or knowing a point on the line and the line’s slope. Depending on what you know about any given line, one of these methods can work. However, what if you only know two points that are on a line? Again, your algebra skills will help you find the equation.
Finding the Equation of a Line from Two Points on the Line
Consider the line that goes through the points (1,2) and (3,6). Can you find the equation that describes this line?
You know the slope-intercept formula is y = mx + b, where (x,y) is a point on the line, m is the slope of the line, and b is the y-intercept of the line. But knowing two of the points on the line doesn’t really seem that helpful.
JUST A MINUTE
Recall that the slope—the ratio of rise to run—of a line can be found by subtracting the y values of the two ordered pairs for the rise and subtracting the x values for the run.
However, you can find the slope by using the rise-to-run ratio from Hour 15. With the two given points—(1,2) and (3,6)—the rise is 2 - 6 = -4, and the run is 1 - 3 = -2:
Because you are given two of the points on this line, choose one point and put its x and y values into y = mx + b. Let’s choose the point (1,2). The equation that can be solved to find b follows:
y = mx + b
2 = 2 · 1 + b
2 = 2 + b
2 - 2 = 2 + b - 2
0 = b
2 = 2 · 1 + b
2 = 2 + b
2 - 2 = 2 + b - 2
0 = b
With m = 2 and b = 0, the equation for the line containing the points (1,2) and (3,6) is y = 2x + 0 or simply y = 2x.
JUST A MINUTE
You can use either of the two given points when substituting the x and y values into y = mx + b. Any line has only one slope, and both points will lead you to the same b value (y-intercept) for the line.
What if you had chosen the point (3,6)? The slope is still 2, and the equation would be this:
y = mx + b
6 = 2 · 3 + b
6 = 6 + b
6 - 6 = 6 + b - 6
0 = b
6 = 2 · 3 + b
6 = 6 + b
6 - 6 = 6 + b - 6
0 = b
With either point on the line, the equation is the same: y = 2x + 0 or y = 2x.
Follow the solution steps in the next example.
Find the equation of the line that contains the points (-1,4) and (3,-8).
Solution: Find the slope of the line and then choose one of the given points for the x and y values in y = mx + b: 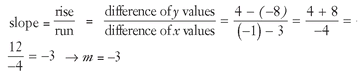
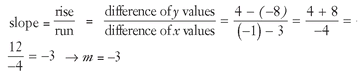
Choose the point (-1,4). The equation becomes:
y = mx + b
4 = -3 · -1 + b
4 = 3 + b
4 - 3 = 3 + b - 3
1 = b
4 = -3 · -1 + b
4 = 3 + b
4 - 3 = 3 + b - 3
1 = b
With m = -3 and b = 1, the equation for the line containing the points (-1,4) and (3,-8) is y = -3x + 1.

Graphing the ordered pairs (-1,4) and (3,-8) confirms that the line going through these two points does have a y-intercept of +1.
A good way to verify this answer is to put the point you didn’t choose, (3,-8), into the equation:
y = -3x + 1 → -8 = -3 · 3 + 1 → -8 = -9 + 1 → -8 = -8
The point (3,-8) does make the equation true and validates your answer.
Now try to write the equation for each of the following lines, checking your answers on page 217.
6. Find the equation of the line that contains the points (-3,-1) and (9,3).
7. Find the equation of the line that goes through (-1,8) and (2,-4).
Next you’ll finish this hour by seeing some real-life applications of equations that include both x and y variables.
Solving Direct Variation Problems
In one of the earlier examples, the equation for the line that contains the points (1,2) and (3,6) is y = 2x + 0 or y = 2x. The ordered pair (1,2) shows that when x = 1, y = 2; the other ordered pair (3,6) shows that when x = 3, y = 6.
Can you predict the y value for the ordered pair if x = 5? The equation y = 2x certainly helps you see that if x = 5, then y = 10, because putting 5 in for x gives the following equation:
y = 2x → y = 2 · 5 → y = 10
Think about the real-life situation of paying $2 per jar for strawberry jam at the farmer’s market. You know without doing any heavy algebra that three jars will cost $6, four jars will be $8, and so on.
Buying jars of this jam is a perfect example of direct variation. The cost ( y) rises constantly as you buy more jars (x), and it rises at a constant rate—each additional jar you buy, you pay $2 more. Another way to say this is that y varies directly as x.
STRICTLY DEFINED
A direct variation equation is based on the slope-intercept formula y = mx + b, and b is always 0. Every direct variation equation can be written as y = mx. The effect is that as x increases, y also increases, and as x decreases, so does y. This “direct change” relationship between x and y is the reason for calling this siutation direct variation.
The cost of the jam is based on the algebra equation y = 2x, where x is the number of jars and y is the total cost, and there is no price break for volume purchases here.
Buying jars of jam can be described as an example of “y varies directly as x” because as x increases, so does y; as x decreases, so does y.
Think of the algebra side of this story: the equation y = 2x has a slope (m) of 2 and a y-intercept (b) of 0. The graph of this equation would go through (0,0). With a slope of 2, the line would rise two units for every one unit of run because slope is the ratio of rise to run.
The line would rise to the right because the slope is positive, and the line would never end. There is an end to the number of jars the farmer can sell—when they’re sold out for the day—but the graphed line goes on infinitely, in both directions.
The graphed line also includes all the ordered pairs between the whole number values, such as (2.5,5) and (3.4,6.8). In reality, you can’t buy 2.5 jars of jam, but if you could, you would have to pay $5. A more realistic graph of the cost of the jam would be a series of dots beginning with the ordered pair (0,0)—if you buy no jars, you pay no money—and then (1,2), (2,4), (3,6), and so on.
When you can say that y varies directly as x, the general form of the equation is y = kx. When k is 5, the graphed line will be steeper than when k is 2, and y will increase more rapidly when k is 5 than when k is 2.
JUST A MINUTE
Recall that when a line’s equation is in slope-intercept form—y = mx + b—the value of m for a line with a steeper slope will have a larger absolute value than the value of m for a line with a less steep slope. A line that is close to being horizontal has a slope between 0 and 1.
In many areas of research, business, and finance, direct variation plays an important role. For example, the weekly payroll costs for a company vary directly as the total number of full-time employees who are working that week. Last week, the payroll was $31,500 for 45 employees who are each paid on the same pay scale. To meet the expected increase in orders for their product next week, five people who had been laid off during a slowdown are called in to work. What will the payroll costs be?
To set up this situation as a direct variation equation y = kx, you need to know what the k value is. You know that when x is 45, y is 31,500. Put these values into the equation and solve for k:
y = kx
31,500 = k · 45
31,500 ÷ 45 = k · 45 ÷ 45
700 = k
31,500 = k · 45
31,500 ÷ 45 = k · 45 ÷ 45
700 = k
The equation for this situation is y = 700x.
To find the payroll costs for five additional people, the x value will be 50:
y = 700 · 50 → y = 35,000
The payroll costs for the 50 employees next week will be $35,000. This direct variation example depends on each employee receiving equal pay, which is not typical.
A more common direct variation problem is the cookie recipe example. The amount of chocolate chips in a batch of cookies varies directly with the number of cookies. For a large party coming up, you are going to bake 150 cookies, but your recipe will make only 60 cookies and calls for 2 cups of chocolate chips. What amount of chips will you need for the party recipe?
This is a direct variation problem, but be careful of the order. The chips vary directly with the number of cookies, so use y = kx, where y = 2 and x = 60. Solve for k: 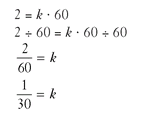
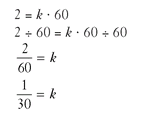
The equation you will now use is 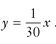 . Put 150 in for x:
. Put 150 in for x: 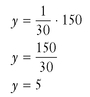
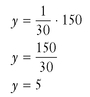
You’ll need 5 cups of chips for the 150 cookies.

Another way to say that one item varies directly with another is to say that one is directly proportional to another. The same equation is used: y = kx.
Now try the following direct variation problems, checking your answers on page 218.
8. The amount you pay for a handyman to shovel snow from your sidewalks varies directly with the time it takes him to finish the job. If you paid him $30 for 20 minutes of his time, what will the bill be after a bigger snowstorm that takes him 50 minutes to clear?
9. The number of items that can be produced by a factory line varies directly with the number of hours the line is running. If the line can assemble 18 items in 4 hours, how many can be produced in 14 hours?
In many real-life situations, as one thing increases, another decreases. The following examples give you algebraic equations that apply in this type of variation problem.
Solving Inverse Variation Problems
When you order a large pizza to share with friends, the more people who want a piece, the smaller each piece will be. This is a great example of inverse variation. As the number of people increases, the size of the slice decreases, which is not at all like direct variation.
STRICTLY DEFINED
An inverse variation equation is based on the equation xy = k and is often written as y = k/x. As x increases, y decreases, and as x decreases, y increases.
Consider the following plans for setting up the chairs for an outdoor wedding. In each row, the space between the chairs gets smaller as the number of chairs in the row increases. If 30 chairs fill the row when they are 12 inches apart, how many chairs can be in the row when they are 8 inches apart?
The inverse equation is xy = k. In this example, x is the number of chairs (30) and y is the space (12) between the chairs. Put 30 in the equation for x, 12 for y, and solve for k:
xy = k
30 · 12 = k
360 = k
30 · 12 = k
360 = k
With k = 360, the equation for the chairs/spaces problem is xy = 360. Put 8 in for y to find the number of chairs:
xy = 360
x · 8 = 360
x · 8 ÷ 8 = 360 ÷ 8
x = 45
x · 8 = 360
x · 8 ÷ 8 = 360 ÷ 8
x = 45
There can be 45 chairs in each row if they are 8 inches apart.
Another example of inverse variation follows:
The speed of a car varies inversely as the time it is traveling. The faster the car’s speed, the less time the trip takes. If your trip home from your friend’s house takes 2 hours and you are going 50 miles per hour, how long will it take you to make the same trip if you go 60 miles per hour?
The inverse variation equation is xy = k. In this example, x is the speed of your car (50) and y is the time (2). Put 50 in the equation for x and 2 for y, and solve for k:
xy = k
50 · 2 = k
100 = k
50 · 2 = k
100 = k
With k = 100, the equation for the problem is xy = 100. Put 60 in for x to find the time for the trip if you go 60 miles per hour:
60y = 100
60y ÷ 60 = 100 ÷ 60
y = 1.7 (rounded up)
60y ÷ 60 = 100 ÷ 60
y = 1.7 (rounded up)
If you go 60 miles per hour, it will take you about 1.7 hours, and 1.7 · 60 is 102 minutes, so the time will be about 18 minutes less than the two hours it takes when you go 50 miles per hour.
Although the graph of the direct variation equation is always a straight line, the inverse variation graph is a curve. So the two types of variation not only apply to different situations, but their equations and graphs are also different.
Now try to solve this inverse variation problem, checking your answer on page 218.
10. When you use a crowbar to move an object, the force you apply varies inversely as the length of the crowbar—the shorter the crowbar, the more force you will need to apply.
If you must use 2 Newtons of force on a crowbar that is 6 feet long, how much force will it take if the crowbar is 4 feet long?
Answers to Sample Problems
1. Slope of line 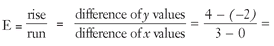
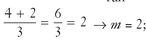 ; the y-intercept is -2 → b = -2; putting m = 2 and b = -2 into y = mx + b → equation of line E is y = 2x - 2
; the y-intercept is -2 → b = -2; putting m = 2 and b = -2 into y = mx + b → equation of line E is y = 2x - 2
2. Slope of line  .
. 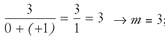 ; the y-intercept is 3 → b = 3; putting m = 3 and b = 3 into y = mx + b → equation of line F is y = 3x + 3
; the y-intercept is 3 → b = 3; putting m = 3 and b = 3 into y = mx + b → equation of line F is y = 3x + 3
3. Slope of line G = -5 → m = -5; y-intercept is 8 → b = 8; putting m = -5 and b = 8 into y = mx + b → equation of line G is y = -5x + 8
4. The ordered pair (-3,2) tells you that x = -3 and y = 2. The slope is -8, so m = -8. To find the b value, put x = -3, y = 2, and m = -8 into y = mx + b:
2 = -8 · -3 + b
2 = 24 + b
2 - 24 = 24 + b - 24
-22 = b
m = -8 and b = -22 → equation of line is y = -8x - 22
2 = 24 + b
2 - 24 = 24 + b - 24
-22 = b
m = -8 and b = -22 → equation of line is y = -8x - 22
5. The ordered pair (5,-6) tells you that x = 5 and y = -6. The slope is -3, so m = -3. To find the b value, put x = 5, y = -6, and m = -3 into y = mx + b:
-6 = -3 · 5 + b
-6 = -15 + b
-6 + 15 = -15 + b + 15
9 = b
m = -3 and b = 9 → equation of line is y = -3x + 9
-6 = -15 + b
-6 + 15 = -15 + b + 15
9 = b
m = -3 and b = 9 → equation of line is y = -3x + 9
6. Find the slope (m) and y-intercept (b) : slope = 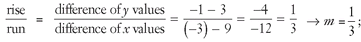 ; from the point (9,3), x = 9, y = 3 → putting x = 9, y = 3, and
; from the point (9,3), x = 9, y = 3 → putting x = 9, y = 3, and 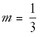 into y = mx + b: 3
into y = mx + b: 3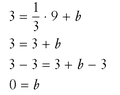
 and b = 0 → equation of the line is
and b = 0 → equation of the line is 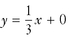 or
or 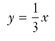 x
x
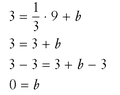
7. Find the slope (m) and y-intercept (b): slope =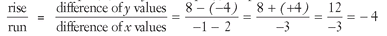 → m = -4; from the point (-1,8), x = -1, y = 8 → putting x = -1, y = 8 and m = -4 into y = mx + b:
→ m = -4; from the point (-1,8), x = -1, y = 8 → putting x = -1, y = 8 and m = -4 into y = mx + b:
8 = -4 · -1 + b
8 = 4 + b
8 - 4 = 4 + b - 4
4 = b
m = -4 and b = 4 → equation of the line is y = -4x + 4
8 = 4 + b
8 - 4 = 4 + b - 4
4 = b
m = -4 and b = 4 → equation of the line is y = -4x + 4
8. Amount you pay ( y) varies directly with worker’s time (x) → y = kx:
30 = k · 20
30 ÷ 20 = k · 20 ÷ 20
1.5 = k
30 ÷ 20 = k · 20 ÷ 20
1.5 = k
The equation is y = 1.5x; put 50 in for x: y = 1.5 · 50 = 75 → you will pay $75 if it takes him 50 minutes to clear the snow.
9. Number of items (y) varies directly with number of hours (x) → > y = kx:
18 = k · 4
18 ÷ 4 = k · 4 ÷ 4
4.5 = k
18 ÷ 4 = k · 4 ÷ 4
4.5 = k
The equation is y = 4.5x; put 14 in for x: y = 4.5 · 14 = 63 → 63 items can be assembled in 14 hours.
10. The force (x) varies inversely as the crowbar’s length (y). The inverse variation equation is xy = k. Put 2 in the equation for x and 6 for y, and solve for k:
xy = k
2 · 6 = k
12 = k
2 · 6 = k
12 = k
With k = 12, the equation for the problem is xy = 12. Put 4 in for y to find how much force you must apply:
x · 4 = 12
x · 4 ÷ 4 = 12 ÷ 4
x = 3
x · 4 ÷ 4 = 12 ÷ 4
x = 3
3 Newtons of force are needed on a 4-foot crowbar.
Review
Hour’s Up!
Based on what you’ve learned in Hour 16, do the following problems. Check your answers with the solution key in Appendix B.
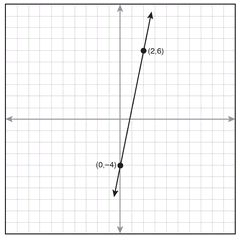
1. 

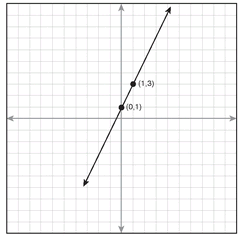
2. 

1. The equation of the line in graph 1 is
a. y = 4x - 5
b. y = 5x - 4
c. y = 5x + 4
d. y = 4x + 5
2. The equation of the line in graph 2 is
a. y = 3x + 2
b. y = 3x + 1
c. y = 2x + 1
d. y = 2x + 2
3. The equation of the line with a slope of -6 and y-intercept of 9 is
a. y = 9x - 6
b. y = 6x + 9
c. y = -6x - 9
d. y = -6x + 9
4. The equation of the line with y-intercept of -5 and a slope of 3 is
a. y = -5x + 3
b. y = 3x + 5
c. y = 3x - 5
d. y = 5x + 3
5. The equation of the line that goes through the point (3,5) and has a slope of -2 is
a. y = -2x + 11
b. y = 2x + 13
c. y = 2x - 11
d. y = -2x + 13
6. The equation of the line that goes through the point (-2,8) and has a slope of 6 is
a. y = 6x + 20
b. y = 6x - 50
c. y = -6x + 20
d. y = -6x - 50
7. The equation of the line that contains the points (2,4) and (-1,-5) is
a. y = -3x - 2
b. y = 3x - 2
c. y = 3x - 10
d. y = -3x - 10
8. The gross amount of your weekly paycheck varies directly with the total dollar amount of sales you make in a gift shop. If your gross paycheck was $600 based on sales of $4,000, what should your paycheck be if you have $5,000 in sales for the week?
a. $650
b. $675
c. $700
d. $750
9. Your new car has been going about 360 miles on each 12-gallon fill up of gas, and the number of miles varies directly with the number of gallons of gas. How many miles can you expect to go on 10 gallons of gas?
a. 300
b. 320
c. 340
d. 280
10. The time it takes you to drive to your friend’s house varies inversely as your average driving speed. (It will take more time to get there if your speed is slower.) The trip takes 3 hours if you drive an average speed of 45 miles per hour. How long will it take if you drive an average of 36 miles per hour due to rainy weather?
a. 3.50 hours, or 3 hours, 30 minutes
b. 3.75 hours, or 3 hours, 45 minutes
c. 4.25 hours, or 4 hours, 15 minutes
d. 4.50 hours, or 4 hours, 30 minutes
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.
