Hour 17
Solving Systems of Equations: Three Methods
The world of two-variable equations that you entered in Hour 15 opens up possibilities of solving problems about direct and inverse variation, as well as being an efficient way to solve many problems that until now were limited to a single variable. This hour you’ll see how to use your graphing skills to find any solutions that two equations may have in common. You’ll also learn two algebraic methods that are very efficient alternatives to graphing. Let’s begin with the graphing method.
Using Graphs to Solve a System of Equations
The equation y = 4x - 2 is graphed in the following figure and labeled line A. A second equation, y = -2x + 4, is also graphed on the same set of axes and labeled line B.
All of the points on each line represent the solutions for each of the equations. Notice the point (1,2), where the two lines cross. Because it is on both lines, the ordered pair (1,2) is a solution for both of the equations. Check this by putting x = 1 and y = 2 into each equation:
Line A: y = 4x - 2 → 2 = 4 · 1 - 2 → 2 = 4 - 2 → 2 = 2
Line B: y = -2x + 4 → 2 = -2 · 1 + 4 → 2 = -2 + 4 → 2 = 2
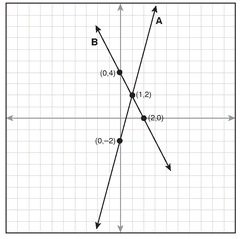
This confirms that (1,2) is a solution of both equations, and this will be helpful when you try to solve real-life problems that have two or more equations to describe a situation. The system of equations in this example is made up of y = 4x - 2 and y = -2x + 4, and you solve the system by finding the point where the two lines intersect: (1,2). This system has one solution because the lines meet at exactly one point.
STRICTLY DEFINED
A system of equations is two (or more) equations that have two (or more) variables. The systems in this book have two equations in two variables. Three or more equations and variables are higher-level algebra topics.
Now consider the following system of equations and the graph of each line.
line A: y = 4x - 2 and line C: y = 4x + 3
The same line A is graphed on the following page, along with line C. Notice that there is no point where the two lines cross. When two lines have the same slope and different y-intercepts, they will not meet and are called parallel lines. If the lines don’t cross, no point is on both the lines, so this system has no solution. No single ordered pair will work in both of these equations.
So far, you have seen an example of a system of equations that has one solution and a system with no solution. This third system might surprise you.
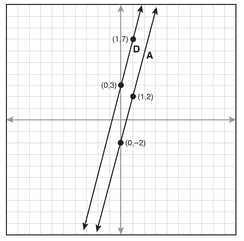
This system of equations is shown in the following graph:
line A: y = 4x - 2 and line D: 12x - 3y = 6
JUST A MINUTE
To write an equation with x and y variables in slope-intercept form, you need to isolate the y variable or solve the equation for y. The properties of addition, subtraction, multiplication, and division help you move the terms so that you can see the m and b values and graph the line.
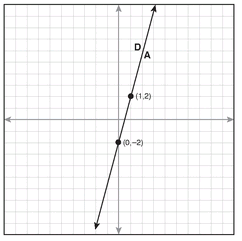
Again, line A is graphed here. On the graph, line D appears to be the same line. How can it be exactly the same line? Follow the steps of moving the terms in the equation for line D so that it is in slope-intercept form, or y = mx + b form, which is the easiest way to graph an equation’s line:
line D: 12x - 3y = 6
12x - 3y = 6
12x - 3y - 12x = 6 - 12x
-3y = 6 - 12x
-3y ÷ -3 = (6 - 12x) ÷ -3
y = 6 ÷ -3 - 12x ÷ -3
y = -2 + 4x
y = 4x + (-2)
y = 4x - 2
12x - 3y = 6
12x - 3y - 12x = 6 - 12x
-3y = 6 - 12x
-3y ÷ -3 = (6 - 12x) ÷ -3
y = 6 ÷ -3 - 12x ÷ -3
y = -2 + 4x
y = 4x + (-2)
y = 4x - 2
As it turns out, the equation for line D, 12x - 3y = 6, is the same as line A: y = 4x - 2. When the equations for lines A and D are graphed, the result is one line. All the points on the one line are solutions for each equation, so this system of equations has an infinite number of solutions.
If solving an equation for y and writing it in slope-intercept form gives an equation that is identical to another equation, their graphs are the same line. Knowing that this system has an infinite number of solutions doesn’t tell you about the solutions themselves. Graphing the line will show you many of the ordered pairs that are solutions to the system.
Now try solving the following system of equations by graphing. Check your answers on page 236.
1. Draw lines E and F on the following graph. Line E: y = 2x - 4 has a y-intercept of -4, has - 1 a slope of 2, and includes points (1,-2) and (2,0). Line F: y = 3 x + 3 has a y-intercept of 3, has a slope of -1/3, and includes the points (3,2) and (6,1). Find the solution of this system of equations, if there is a solution. 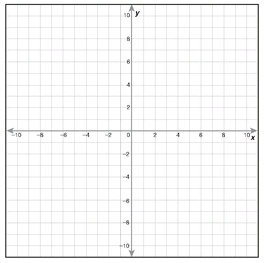

Solving a system of equations by graphing the lines and finding where the lines cross—if they do cross—makes good use of your graphing skills. It gives you a visual representation of the system and its solution, whether there is one, many, or no solution.
However, there are some disadvantages to the graphing method. You might not have graph paper for drawing the lines. The equations might not have convenient slopes or y-intercepts that fit on the graph paper. The point where the two lines meet might not be whole numbers or might exist somewhere beyond the limits of your graph paper and be off the page so you can’t see it.
For all these reasons, there are algebraic methods you can always count on to help you solve a system of equations. You’ll learn about two of these methods in the next sections.
Solving a System of Equations by Substitution
When you are solving a system of equations, your goal is to find the solution, the ordered pair that makes both equations true. Graphing the two lines might show you the answer, but it is not very efficient, and you know by now that algebra is all about efficiency.
One of the basic principles of algebra is used so often that you might not realize it has a formal name. Every time you solve an equation and put the solution back into the original equation to verify that it is correct, you are using the substitution property.
STRICTLY DEFINED
The substitution property states that equal algebraic expressions can be substituted into (or used in place of) other algebraic expressions. For example, if a = 4, then a + 7 = 4 + 7; if x = b + c, then 6x = 6(b + c).
Consider the following system of equations:
y = 3x + 2 and 2x + y = 12
You could graph the lines that represent these two equations to see where the lines meet, if they do meet. An alternative is to realize that the x and y variables appear in both equations, and the x in one is the same as the x in the other; the same is true of the y variables.
The substitution property lets you create a new equation based on the two equations in this system. The solution steps follow.
The two equations are y = 3x + 2 and 2x + y = 12. In the first equation, y equals 3x + 2. Therefore, 3x + 2 can be substituted for y in the second equation, like this:
2x + (3x + 2) = 12 The ( ) just emphasize the substitution.
Now you can solve this new equation to find x:
2x + (3x + 2) = 12
5x + 2 = 12
5x + 2 - 2 = 12 - 2
5x = 10
5x ÷ 5 = 10 ÷ 5
x = 2
5x + 2 = 12
5x + 2 - 2 = 12 - 2
5x = 10
5x ÷ 5 = 10 ÷ 5
x = 2
Putting 2 in for x in either equation lets you find y. (The first equation is a little easier to use since the y term is already isolated, so use the first equation.)
y = 3x + 2 → y = 3 · 2 + 2 → y = 6 + 2 → y = 8
Now that you found x = 2 and y = 8, you know the ordered pair where the lines would intersect if you graphed them, and you know the solution to the system: (2,8)
To check your answer, put 2 in for x and 8 in for y in the second equation:
2x + y = 12 → 2 · 2 + 8 = 12 → 4 + 8 = 12 → 12 = 12
This confirms that (2,8) is the solution to the system of equations y = 3x + 2 and 2x + y = 12.
Follow the substitution process as it efficiently finds the solution of this next system of equations.

The equation with an isolated variable will be substituted into the other equation—it might be the first or second equation, and you might need to isolate a variable. For example, in the system 6x + y = 18 and y - 3x = 9, the second equation can become y = 3x + 9 if you add 3x to both sides, and 3x + 9 could be substituted for y in the first equation.
If 5x + y = -3 and y = x - 9, solve this system.
In the second equation, y equals x - 9. Substitute x - 9 in the place of y in the first equation:
5x + (x - 9) = -3
6x - 9 = -3
6x - 9 + 9 = -3 + 9
6x = 6
6x ÷ 6 = 6 ÷ 6
x = 1
6x - 9 = -3
6x - 9 + 9 = -3 + 9
6x = 6
6x ÷ 6 = 6 ÷ 6
x = 1
Put 1 in for x in either equation (the second one is in an easier form, so use it) and solve for y:
x = 1 and y = -8, so (1,-8) is the solution to the system of equations 5x + y = -3 and y = x - 9.
y = x - 9 → y = 1 - 9 → y = -8
When both equations have either isolated y variables or isolated x variables, the substitution method works especially well, as you see in the next example.
If x = -3y + 6 and x = 2y - 9, solve this system.
From the first equation, you know that x equals -3y + 6, so you can put -3y + 6 in the second equation where the x is, creating this new equation that can be solved for y:
-3y + 6 = 2y - 9
-3y + 6 + 3y = 2y - 9 + 3y
6 = 5y - 9
6 + 9 = 5y - 9 + 9
15 = 5y
15 ÷ 5 = 5y ÷ 5
3 = y
-3y + 6 + 3y = 2y - 9 + 3y
6 = 5y - 9
6 + 9 = 5y - 9 + 9
15 = 5y
15 ÷ 5 = 5y ÷ 5
3 = y
Put 3 in for y in the second equation and solve for x:
x = -3 and y = 3, so (-3,3) is the solution to the system of equations x = -3y + 6 and x = 2y - 9.
x = 2 · 3 - 9 → x = 6 - 9 → x = -3
The final example that follows shows a slightly more complex situation, but the process is still exactly the same.
If y = 4x - 2 and 6x - y = 8, solve this system.
In the first equation, y equals 4x - 2. Substitute 4x - 2 in the place of y in the second equation:
6x - (4x - 2) = 8 The ( ) emphasize the subtraction!
GO TO ◀
Subtraction can be changed to addition if you change the signs of all the terms in the second expression (see Hour 3).
Watch the signs as you subtract the binomial 4x - 2. You must change the signs of both the 4x and the -2 when the subtraction changes to addition: subtracting 4x - 2 is really adding -4x + 2.
6x - (4x - 2) = 8
6x + (-4x) + 2 = 8
2x + 2 = 8
2x + 2 - 2 = 8 - 2
2x = 6
2x ÷ 2 = 6 ÷ 2
x = 3
6x + (-4x) + 2 = 8
2x + 2 = 8
2x + 2 - 2 = 8 - 2
2x = 6
2x ÷ 2 = 6 ÷ 2
x = 3
Put 3 in for x in the first equation to solve for y: y = 4x - 2 → y = 4· 3 - 2 → y = 12 - 2 → y = 10 x = 3 and y = 10, so (3,10) is the solution to the system of equations y = 4x - 2 and 6x - y = 8.
Now try to solve these systems of equations using the substitution method. Check your answers on page 236.
2. If y = 3x - 4 and x + y = 16, solve this system.
3. If 4x - y = 3 and y = -5x - 12, solve this system.
When you are solving a system of equations that includes an equation with one of the variables isolated, as in the previous examples, substitution works very well. If the two equations have no isolated variables, there is still a great alternative to graphing the lines. Let’s finish this hour with another algebraic method.
Solving a System of Equations by Addition
Back in Hour 5, you learned that the addition property is helpful when you want to solve an equation like x - 5 = 3. Without much hesitation, you would add 5 to both sides and solve for x:
x - 5 + 5 = 3 + 5
x = 8
x = 8
The addition property of equality states that adding the same number to equal expressions gives equal sums. This property isn’t limited to helping you move numbers from one side of an equation to the other to isolate a variable, as in the previous simple equation.
Remember that the equals sign is the powerful symbol that connects two expressions that are equal to each other. The addition property says that when you add equal items to equal expressions, you have expressions that remain equal.
JUST A MINUTE
Terms can be combined with adding and subtracting when they are like terms. They must be the same variable with equal exponents (in these equations, all the variables have exponents of 1). Their coefficients (the number in front of each variable) are then combined. Exponents never change when terms are added or subtracted.
For example, if x + y = 8 and 5x + 2y = 6, the addition property allows these equations to be added together. The expressions on the left side of the equals sign are combined to produce 6x + 3y, and the expressions on the right side of the equals sign are combined to produce a sum of 14. Therefore, 6x + 3y = 14 is the result when adding these two equations together. The like terms are combined, and no terms are moved or rearranged in any way. In this particular example, it isn’t really of great help that the two separate equations created the new one—6x + 3y = 14 is still an equation with two variables, just as the two equations were to begin with.
However, adding certain equations together will result in a very convenient new equation, as in the next example:
Consider the system of equations x + y = 30 and x - y = -6. You can graph the two lines to see where they cross, but the first equation has a y-intercept of 30, so the line won’t fit on a typical coordinate graph numbered from -8 to +8. Substitution would also work, but you would have to isolate one of the variables first. There is a better way, and it’s all about addition.
You need to add these two equations, and the clearest way to see the adding process is to stack the equations vertically, as they are shown here: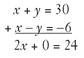
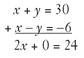
The y variables sum to 0, and the new equation has only the x variable. Solving for x is easily done: divide both sides by 2, and the rest of the solution follows the same process as in the substitution method.
2x = 24
2x ÷ 2 = 24 ÷ 2
x = 12
2x ÷ 2 = 24 ÷ 2
x = 12
Put 12 in for x in the first equation and solve for y:
x = 12 and y = 18, so (12,18) is the solution to the system of equations x + y = 30 and x - y = -6.
12 + y = 30 → 12 + y - 12 = 30 - 12 → y = 18
TIME SAVER
You have learned how to use three methods for solving systems of equations: graphing, substitution, and addition. Decide which is most efficient based on the type of equations in each system.
You have three options when you are solving systems of equations, and addition is the perfect choice when the coefficients of either the x or y variables are opposites.
Adding opposites always results in 0, so this is an effective way to eliminate one of the variables in a system of equations. The following example shows detailed solution steps in a system of equations with opposite coefficients on the x variables:
If -3x - 2y = -19 and 3x - 5y = 5, solve this system.
Solution: -3x and 3x are opposites. Stack the equations vertically and add them to make a new equation with only the y variable: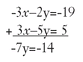
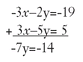
Dividing both sides of this equation by -7 → y = 2.
Put 2 in for y in the second equation:
x = 5 and y = 2, so (5,2) is the solution to the system of equations -3x - 2y = -19 and 3x - 5y = 5.
3x - 5y = 5 → 3x - 5 · 2 = 5 → 3x - 10 = 5 → 3x - 10 + 10 = 5 +
10 → 3x = 15 → 3x ÷ 3 = 15 ÷ 3 → x = 5
10 → 3x = 15 → 3x ÷ 3 = 15 ÷ 3 → x = 5
Now try to solve the following systems of equations with the addition method. Check your answers on page 236.
4. If x - y = 9 and x + y = 5, solve this system of equations.
5. If 3x + 13y = 9 and -3x + 5y = 45, solve this system of equations.

Parallel lines have equal slopes (m) and different y-intercepts (b). If you write two equations in a system in the slope-intercept form of y = mx + b and their m values are equal and their b values are not—then you know there is no solution to the system.
At the beginning of this hour, the graphing method of solving systems included a system of equations that had no solution because the lines did not cross but were parallel. Also, two of the equations made graphs of exactly the same line, so there were infinitely many solutions—all the points on that line. It is possible to have no solution or many solutions when you use the substitution or addition methods, as you will see in the next two examples.
If y = 3x - 2 and 3x - y = 8, solve the system.
Solution: Because the y variable is isolated in the first equation, use substitution. Put 3x - 2 in for y in the second equation and solve for x:
3x - (3x - 2) = 8
3x + (-3x) + 2 = 8
0 + 2 = 8
2 = 8
3x + (-3x) + 2 = 8
0 + 2 = 8
2 = 8
However, 2 cannot equal 8, so there is no solution to this system of equations—no ordered pair exists that makes both of these equations true at the same time. If you do graph these lines, they will be parallel and will confirm that there is no solution.
JUST A MINUTE
Parallel lines have equal slopes and different y-intercepts, and they never cross; no ordered pair exists that can make both the equations true if the equations graph into parallel lines.
If 2x + y = 4 and y = -2x + 4, solve the system.
Solution: The y variable is isolated in the second equation, so use substitution. Put -2x + 4 in for y in the first equation and solve for x:
4 does always equal 4, so this system has infinitely many solutions. If you graph these two lines, they will form exactly the same line, and the solutions to the system are all the points on this line. You might also note that if you solve the first equation for y by subtracting 2x from both sides, the equation becomes exactly the same as the second equation. This confirms that there are infinitely many solutions to this system of equations.
2x + (-2x + 4) = 4. The ( ) show -2x + 4 being put in for y.
0 + 4 = 4
4 = 4
0 + 4 = 4
4 = 4
Now try to solve this system of equations. It will have either infinitely many solutions or no solution. Check your answer on page 237.
6. If 6x + y = 8 and y = -6x + 3, solve this system of equations.
To summarize this hour of solving systems of equations:
Graphing can show the solution to a system, but it is only the preferred method if both of the equations are in slope/intercept form, you have access to graph paper, and the slope and y-intercept values are simple and can fit on your graph.
Substitution is the preferred method if one—or both—of the equations has an isolated variable, allowing you to substitute what it equals into the other equation in that variable’s place.
Addition is the preferred method if the coefficients of the x or y variables are opposites. This allows you to add the two equations, and the opposites will sum to 0, creating a new equation in one variable that is easily solved.
In both substitution and addition, remember to put the first known variable’s value back into one of the equations to solve for the second variable. Your goal is to find the ordered pair that makes both the equations in the system true at the same time, so you need to find both the x and y values that make the equations true.
Answers to Sample Problems
1. The lines are graphed in the following, and the solution of this system is (3,2).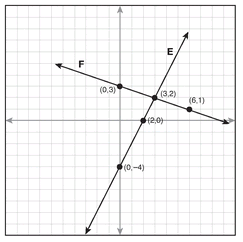

2. Put 3x - 4 into the second equation for y → x + (3x - 4) = 16 → > 4x - 4 = 16 → 4x - 4 + 4 = 16 + 4 → 4x = 20 → 4x ÷ 4 = 20 ÷ 4 → x = 5; put 5 in for x in the first equation and solve for y: y = 3 · 5 - 4 → y = 15 - 4 → y = 11. Solution is (5,11).
3. Put -5x - 12 into the first equation for y → 4x - (-5x - 12) = 3 → > 4x + 5x + 12 = 3 →. 9x + 12 = 3 → 9x + 12 - 12 = 3 - 12 → 9x = -9 → 9x ÷ 9 = -9 ÷ 9 → x = -1; put -1 in for x in the first equation and solve for y: 4 · -1 - y = 3 → -4 - y = 3 → -4 - y + 4 = 3 + 4 → -y = 7 → -y ÷ -1 = 7 ÷ -1 → y = -7. Solution is (-1,-7).
4. 

Divide both sides by 2 → x = 7; put 7 in for x in the second equation. Solve for y: 7 + y = 5 → 7 + y - 7 = 5 -7 → y = -2. Solution is (7,-2).
5. 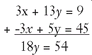
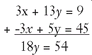
Divide both sides by 18 → y = 3; put 3 in for y in the first equation and solve for x : 3x + 13 · 3 = 9 → 3x + 39 = 9 → 3x + 39 - 39 = 9 - 39 → 3x = -30 → 3x ÷ 3 = -30 ÷ 3 → x = -10. Solution is (-10,3).
6. Use substitution: put -6x + 3 into the first equation for y and solve for x: 6x + (-6x + 3) = 8 → 0 + 3 = 8 → 3 = 8. However, 3 cannot equal 8, so this system has no solution.
Review
Hour’s Up!
Based on what you’ve learned in Hour 17, find the solutions for the following systems of equations using the graphing, substitution, or addition methods. Check your answers with the solution key in Appendix B.
1. line G: y = x - 3 and line H: y = -2x + 3
The slope of line G is 1 and points include (0,-3) and (3,0); the slope of line H is -2 and points include (1,1) and (0,3).

a. (1,-2)
b. (2,-1)
c. Infinitely many solutions
d. No solution
2. line I: y = 2x + 3 and line J: y = 2x - 1 The slope of line I is 2 and points include (0,3) and (-1,1); the slope of line J is 2 and points include (0,-1) and (2,3).

a. (1,0)
b. (0,3)
c. Infinitely many solutions
d. No solution
3. y = -2x + 2 and 3x + y = 5
a. (-3,4)
b. (3,-4)
c. Infinitely many solutions
d. No solution
4. x - 3y = 8 and x = 2y + 7
a. (5,-1)
b. (2,3)
c. Infinitely many solutions
d. No solution
5. y = 5x + 1 and 5x - y = 3
a. (-1,3)
b. (3,-1)
c. Infinitely many solutions
d. No solution
6. 4x + y = 6 and y = 6 - 4x
a. (6,6)
b. (0,6)
c. Infinitely many solutions
d. No solution
7. 2x + 3y = 6 and 4x - 3y = 12
a. (3,0)
b. (0,3)
c. Infinitely many solutions
d. No solution
8. 3x - 2y = 1 and -3x + 2y = 7
a. (0,8)
b. (8,0)
c. Infinitely many solutions
d. No solution
9. 2x - y = 5 and -x + y = -3
a. (1,-2)
b. (2,-1)
c. Infinitely many solutions
d. No solution
10. 3x - 2y = -6 and -2x + 2y = 2
a. (-4,-3)
b. (-3,-4)
c. Infinitely many solutions
d. No solution
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.
