Hour 15
Equations with Two Variables: Graphing
The real-life applications of ratios, proportions, and percents in the previous two hours of study brought together your knowledge of polynomials, algebraic fractions, and simplifying expressions. The variety of real-world problems you can now solve is a perfect example of why it’s important to understand and use algebra with confidence.
Think back for a moment to solving equations. Your goal in solving all the equations so far has been to isolate the variable. Each equation had a single variable, although sometimes it appeared on both sides of the equals sign. This hour marks a turning point in your study of algebra. Most of the work from now on focuses on working with two different variables in each equation, which will expand your thinking skills greatly!
Plotting Ordered Pairs on a Graph
The number line lets you graph points anywhere along its length, whether the number is positive, negative, zero, a whole number, a fraction, or a decimal—each number has its place somewhere on the number line. An equation with one variable might have one solution, or it might have no solution, as in the following examples.
Solve: x - 2 = 3
Solution: x - 2 + 2 = 3 + 2 → x = 5
Graph the solution on a number line:
Solve: x + 4 = x + 3
Solution: x + 4 = x + 3 → x + 4 - x = x + 3 - x → 4 = 3
Because 4 cannot equal 3, this equation has no solution.
An equation with two different variables might have many solutions, as in the next example.
Solve: x + y = 6
Solution: With two variables, x and y can be many possible answers, including x = 1 when y = 5. Instead of having a single answer, this equation has a pair of numbers as an answer. To graph this solution, you need a two-dimensional graph.
This new graph begins with the number line you have been using for plotting points. Through the zero point on that line, a vertical line is drawn. This new line is labeled with positive numbers above the zero and negative numbers below the zero.
The horizontal line is called the x-axis, and the vertical line is the y-axis. The point you are graphing has an x value of 1 and a y value of 5. The most efficient way to describe these values is as a pair of numbers:
(x,y) → (1,5)
Another possible solution to the equation x + y = 6 is x = 4 when y = 2, and that pair of numbers would be written:
(x,y) → (4,2)
To graph these two ordered pairs, begin with the first pair, (1,5). Because x = 1, find +1 on the horizontal line (the x-axis). Because y = 5, rise up 5 marks to +5. This point is shown on the following graph.
STRICTLY DEFINED
An ordered pair is a pair of numbers that represents a solution to an equation with two variables. It is called an “ordered” pair because the location of (3,4) is not the same as the location of (4,3).
The second pair, (4,2), is graphed similarly: because x = 4, find +4 on the x-axis, then rise up 2 marks to +2. These two points have been graphed in the following figure, with arrows showing the process:

Ordered pairs can also have negative numbers as one or both of the values. To graph (5,-3), begin at +5 on the x-axis, then go down 3 marks to -3. If the ordered pair is (-4,3), begin at -4, to the left of 0 on the x-axis, then go up 3 to +3. This graphing process for each of these points follows :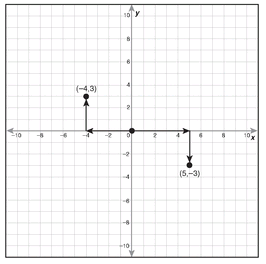



The point (0,0) is often called the origin because you start at (0,0) when you graph each ordered pair. An ordered pair can also have 0 as the x or y value: the point (0,4) is up 4 on the y-axis; the point (-3,0) is 3 to the left on the x-axis.
Now try graphing the following ordered pairs on the following graph, checking your answers on page 194.
1. (6,2)
2. (-2,- 4)
3. (-5,5)
Graphing ordered pairs helps you find many of the solutions for equations with two variables, as you will learn in the next section.
Graphing Two-Variable Equations Using the Intercepts
As you saw in the earlier equation sample, when there are two different variables in an equation, there are many solutions, shown as ordered pairs.
Look again at the equation x + y = 6. Two of the ordered pair solutions you graphed on the axes were (1,5) and (4,2). Plot them again on the following graph:

With the edge of a ruler, index card, or any straightedge, draw the line to connect these two points, extending the line up past and down below both points, going as far as you can in both directions while still staying on the graph. Did your line go through any other whole-number points? If you graphed the points correctly and drew the line joining them carefully, the line should go through each of these points: (0,6), (2,4), (3,3), (5,1), and (6,0).
Putting each of these pairs of numbers into the equation x + y = 6 should make a true equation. For example, the ordered pair (0,6) would become 0 + 6 = 6, which is true. In fact, each point’s x and y values will sum to 6.
This tells you that if you can find just two ordered pairs that make an equation true, graphing those points and drawing the line that connects them will show you all the ordered pairs that make the equation true.
Return once again to that sample equation, x + y = 6. The two ordered pairs that are the easiest to find are when x = 0, so y = 6 and when y = 0, so x = 6. These ordered pairs are (0,6) and (6,0). Graphing those in the very beginning and drawing the line that connects them gives you all the other solutions that are listed above.
In fact, the points (0,6) and (6,0) are so helpful as you try to find the solutions to the equation that they have special names:
(0,6) is where the line meets the y-axis, so (0,6) is called the y-intercept.
(6,0) is where the line meets the x-axis, so (6,0) is called the x-intercept.
Together the points (0,6) and (6,0) are called the intercepts, and they are not only easy to find from the original equation, but they are easy to plot on the graph.
Look back at your graph of x + y = 6. The line should have also gone through other easily named points, including (-1,7) and (-2,8), as well as (7,-1) and (8,-2). Notice that each of these ordered pairs makes a true statement when they are put into the equation x + y = 6. They are all certainly solutions, just as the points listed previously are.
There is actually an infinite number of points on this line that are all solutions for the equation, and they include all the whole-number pairs such as (9,-3) and (10,-4). But don’t stop there—all the fractional and decimal ordered pairs on this same line are also solutions, including (2.5,3.5), (2.51,3.49), and (-1.3,7.3).
STRICTLY DEFINED
An infinite number of points means that there are so many, they cannot be counted; the concept of an infinite number indicates that the number increases without an upper bound or is never-ending.
The list is endless, but the good news is that by drawing the line that connects any two of the easily found solutions, you are able to show all the solutions because the solutions are all the points on the line.
Let’s look at another equation and graph its intercepts:
x - y = 2
Solution: Let x equal 0 → 0 - y = 2
To solve 0 - y = 2, adding y to both sides makes the equation a little easier to work with:
0 - y + y = 2 + y → 0 = 2 + y → 0 - 2 = 2 + y - 2 → -2 = y
So (0,-2) is a solution for this equation, and it’s an intercept on the graph.
Now let y equal 0 → x - 0 = 2 → x = 2.
So (2,0) is a solution for this equation, and it’s also an intercept on the graph.
Plot these two key points on the following graph. Connecting them shows you the line containing every ordered pair that is a solution to this equation.
Your line should go through (6,4) and (-1,-3), as well as many others. Each of these ordered pairs makes a true statement when they are put into x - y = 2.
Now try to graph the intercepts of the following equations, draw the line, and list two other ordered pairs that are also solutions. Check your answers on pages 194-195.
4. x + y = 5
5. x + y = -6
The graphs of the two equations in previous problems 4 and 5 resulted in lines that are not horizontal or vertical. Comparing the lines, you see that both slant downward to the right. Your skills with ratios will help you analyze these and other lines in the next section.
Finding the Slope of a Line, Given Two Points
Consider the lines in the two following graphs. Line A connects the points (0,0) and (4,4), and line B connects the points (0,0) and (1,4). Each line has been extended above and below the points a short distance.

As you read the following facts about lines A and B, refer to the previous graphs.
Both lines are slanted, and they both rise to the right, with the second line rising more steeply.
Both lines go through (0,0), with line A going through (4,4), while line B rises more steeply and goes through (1,4).
In algebra, the word that describes a line’s slant is slope. The slope of a line is the ratio of a line’s rise to its run. You’ll use a formula to find this ratio, but let’s look at two examples first:
Lines A and B have been drawn again on the following graphs, and this time the rise and run of each line are labeled.
STRICTLY DEFINED
A line’s slope is the steepness of the line as you move from one point to another along the line. Slope is based on how much the line rises compared to its horizontal change, which is the ratio of rise to run.
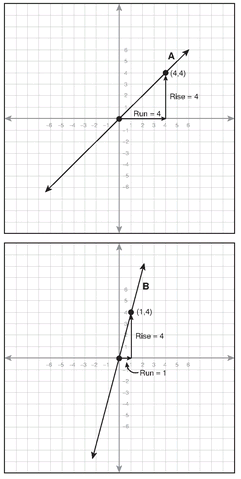
Line A’s ratio of rise to run is 4:4, or 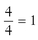 .
.
Line B’s ratio of rise to run is 4:1, or 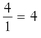 .
.
Line B is rising more steeply than line A. Line B’s slope is 4, which is much higher than line A’s slope of 1. This is consistent with the slopes of all graphed lines: the steeper the line, the higher the absolute value of the slope.
Now try to find the slope of the following lines that are graphed here, checking your answers on page 195.
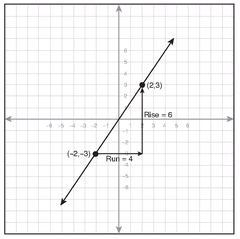
6.

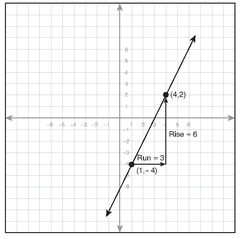
7.

When an equation is graphed, you have a visual image of the line’s slope. In the previous graphs, the rise and run are labeled for you, so finding the ratio of rise to run is easy. Also, both lines A and B are rising to the right, and their slopes are positive, which is true for all lines that rise to the right.
STRICTLY DEFINED
The rise of a line is the difference of the y values of two ordered pairs on that line. The run of a line is the difference of the x values of two ordered pairs on the line.
Looking at the graphed line does allow you to find the rise and run by counting. But there’s also a way to find the rise and run without even seeing the line—all you need to know are the two ordered pairs that are on the line.
The rise is found by subtracting the y values of the two points, and the run is found by subtracting the x values of the same two points.
Try this method with a line that you already know the slope of, such as the line that goes through (0,0) and (1,4):
The y values of the ordered pairs are 0 and 4, so the rise is 0 - 4= -4.
The x values of the ordered pairs are 0 and 1, so the run is 0 - 1 = -1.
Slope is the ratio of rise to run → -4 to 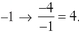 .
.
You know the slope is 4 from using the rise and run labeled on the graph. You found the same slope by calculating the rise and run with the subtraction method.
Knowing two points on a line enables you to find the slope of that line without having to graph the line, and the subtraction method is in formula form here:
PROCEED WITH CAUTION
Be careful to use the y values of the ordered pairs as the numerator and the x values in the denominator when finding the slope of a line: the ratio of 4 to 3 is not the same as the ratio of 3 to 4.
For example, if the points (2,3) and (6,8) are on the line, to find the slope of this line, find the rise and run as follows:
The slope of the line containing (2,3) and (6,8) is 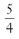 .
.
What if you listed the same two points as (6,8) and (2,3)? Will the slope be the same?
Yes, the slope is the same. If you graphed these two ordered pairs and drew the line connecting them, there is only one line—it doesn’t matter which point you happen to graph before the other, so of course the slope is the same number, no matter which point you may choose as the “starting point.”
All the slopes in this section have been positive, but slopes can be negative. Lines that fall to the right have negative slopes, as in the following example:
Find the slope of the line containing the points (3,5) and (7,0):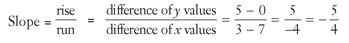
Graphing these two points would show you that the line does fall to the right, but using the slope formula confirms it. The slope of the line containing the points (3,5) and (7,0) is  .
.
The final example shows how to find the slope when one or more of the x or y values in the ordered pairs are negative:
Find the slope of the line containing the points (-2,6) and (-5,-3):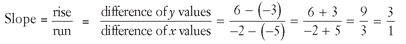
If you are careful with the subtraction process and watch the negative signs of the terms, your algebra skills will get you through this more complex-looking problem easily.
Now try to find the slope of the line containing the following points, checking your answers on page 195.
8. (0,8) and (10,0)
9. (-5,3) and (-2,-1)
Answers to Sample Problems
1., 2., 3.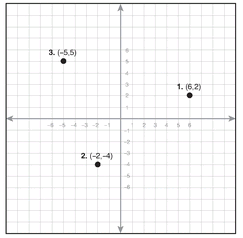

4. x + y = 5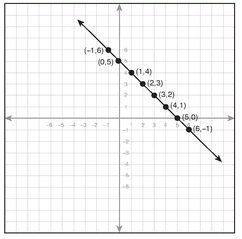

5. x + y = -6

6. The slope of the line is the ratio of rise to run. 
7. The slope of the line is the ratio of rise to run.  2
2
8. (0,8) and (10,0) → Slope =
9. (-5,3) and (-2,-1) → Slope =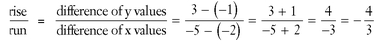
Review
Hour’s Up!
Based on what you’ve learned in Hour 15, do the following problems. Check your answers with the solution key in Appendix B.
For problems 1 through 4, graph the intercepts of the following equation, and draw the line connecting the intercepts. Choose the ordered pair in each problem that is on the graphed line.
1. x + y = -3
a. (2,5)
b. (3,0)
c. (2,-5)
d. (1,-5)

2. x + y = 7
a. (8,1)
b. (8,-1)
c. (1,8)
d. (1,-8)

3. 2x + y = 4
a. (2,-3)
b. (3,2)
c. (3,-2)
d. (2,3)

4. x - y = 4
a. (-1,-5)
b. (-5,-1)
c. (1,-5)
d. (0,4)

5. Find the slope of the line in the following graph: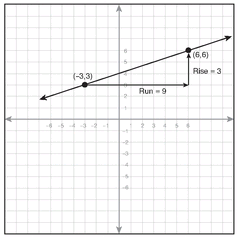
a. 3
b. 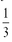
c. 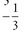
d. -3

6. Find the slope of the line graphed next:
a. 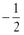
b. 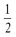
c. 2
d. -2

7. Find the slope of the line containing the points (2,4) and (6,10).
a. 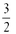
b. 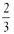
c. 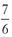
d. 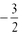
8. Find the slope of the line containing the points (-3,8) and (5,2).
a. 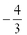
b. 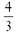
c. 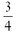
d. 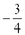
9. Find the slope of the line containing the points (-1,-7) and (-3,7).
a. 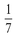
b. 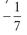
c. -7
d. -1
10. Find the slope of the line containing the points (0,-4) and (6,-8).
a. 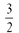
b. 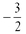
c. 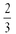
d. 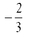
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.
