Chapter 6
Analyzing Categorical Time Series
In Part II of this book, we shall be concerned with categorical processes ![]() ; that is, the range
; that is, the range ![]() of
of ![]() is not only assumed to be discrete, but also to be qualitative, consisting of a finite number
is not only assumed to be discrete, but also to be qualitative, consisting of a finite number ![]() of categories, with
of categories, with ![]() (state space). The time series
(state space). The time series ![]() stemming from this kind of process are referred to as categorical time series. In some applications, the range of
stemming from this kind of process are referred to as categorical time series. In some applications, the range of ![]() exhibits at least a natural ordering; it is then referred to as an ordinal range. In other cases, not even such an inherent order exists (a nominal range). In Brenčič et al. (2015), for instance, time series about atmospheric circulation patterns are analyzed. Each day is assigned 1 out of 41 categories, called elementary circulation mechanisms (ECMs); although there are some relationships (similarities) between these categories (for example, they can be arranged in four groups), the categories do not exhibit an inherent ordering; that is, we are concerned with a nominal range. In contrast, Chang et al. (1984) consider time series for daily precipitation and distinguish between dry days, days with medium or with strong precipitation, thus leading to an ordinal time series. Another example of nominal “time” series are nucleotide sequences (a range of four DNA bases) and protein sequences (twenty amino acids) (Churchill, 1989; Krogh et al., 1994; Dehnert et al., 2003), although again similarities exist within these types of nominal range (Taylor, 1986). The time series of electroencephalographic (EEG) sleep states (per minute), as analyzed by Stoffer et al. (2000), are also ordinal time series.
exhibits at least a natural ordering; it is then referred to as an ordinal range. In other cases, not even such an inherent order exists (a nominal range). In Brenčič et al. (2015), for instance, time series about atmospheric circulation patterns are analyzed. Each day is assigned 1 out of 41 categories, called elementary circulation mechanisms (ECMs); although there are some relationships (similarities) between these categories (for example, they can be arranged in four groups), the categories do not exhibit an inherent ordering; that is, we are concerned with a nominal range. In contrast, Chang et al. (1984) consider time series for daily precipitation and distinguish between dry days, days with medium or with strong precipitation, thus leading to an ordinal time series. Another example of nominal “time” series are nucleotide sequences (a range of four DNA bases) and protein sequences (twenty amino acids) (Churchill, 1989; Krogh et al., 1994; Dehnert et al., 2003), although again similarities exist within these types of nominal range (Taylor, 1986). The time series of electroencephalographic (EEG) sleep states (per minute), as analyzed by Stoffer et al. (2000), are also ordinal time series.
Here, unless stated otherwise, we shall consider the more general case of a nominal range. So even if there is some ordering, we do not make use of it but assume that each random variable ![]() takes one of a finite number of unordered categories. To simplify notation, we adapt the convention from Appendix B.2 and assume the possible outcomes to be arranged in a certain lexicographical order,
takes one of a finite number of unordered categories. To simplify notation, we adapt the convention from Appendix B.2 and assume the possible outcomes to be arranged in a certain lexicographical order, ![]() .
.
As discussed in the context of Example A.3.3, a categorical random variable ![]() can be represented equivalently as a binary random vector
can be represented equivalently as a binary random vector ![]() , with the range consisting of the unit vectors
, with the range consisting of the unit vectors ![]() , by defining
, by defining ![]() if
if ![]() . We shall sometimes switch to this kind of representation, referred to as a binarization, if it allows us to simplify expressions.
. We shall sometimes switch to this kind of representation, referred to as a binarization, if it allows us to simplify expressions.
6.1 Introduction to Categorical Time Series Analysis
For (stationary) real-valued time series, a huge toolbox for analysis and modeling is readily available and well known to a broad audience. To highlight a few basic approaches, the time series are visualized by simply plotting the observed values against time, the marginal properties such as location and dispersion may be measured in terms of mean/median and variance/quartile range, respectively, and serial dependence is commonly quantified in terms of autocorrelation; see also Section 2.4.
Things change if the time series is categorical. As an example, since the elementary mathematical operations are not applicable for such a qualitative range, moments like the mean or the autocovariance can no longer be computed. In the ordinal case, at least a few methods can be preserved. For example, a time series plot is still feasible by arranging the possible outcomes in their natural ordering along the Y-axis, and the location can be measured by the median (more generally, quantiles and cdf are defined for ordinal data). But in the purely nominal case (as mainly considered here), not even these basic analytic tools are applicable. Therefore, tailor-made solutions are required for visualizing such time series, or for quantifying location, dispersion and serial dependence.
In the sequel, when calling a categorical process ![]() stationary, we refer to the concept of strict stationarity according to Definition B.1.3. While specific models for such stationary categorical processes are discussed in Chapter 7, the particular instance of an i.i.d. categorical process will be of importance here, since it constitutes the benchmark when trying to uncover serial dependence.
stationary, we refer to the concept of strict stationarity according to Definition B.1.3. While specific models for such stationary categorical processes are discussed in Chapter 7, the particular instance of an i.i.d. categorical process will be of importance here, since it constitutes the benchmark when trying to uncover serial dependence.
Table 6.1 Frequency table of infant EEG sleep states data
| State | qt | qh | tr | al | ah | aw |
| Absolute frequency | 33 | 3 | 12 | 27 | 32 | 0 |

Figure 6.1 Time series plot of infant EEG sleep states (per minute); see Example 6.1.1.
An application leading to a visibly non-linear rate evolution graph is presented by Brenčič et al. (2015), who analyzed a time series about atmospheric circulation patterns. Other tools for visually analyzing a categorical time series, such as the IFS (iterated function systems) circle transformation (Weiß, 2008d), look for the occurrence of patterns; that is, the occurrence of tuples (“strings”) ![]() or of sets of such tuples. A comprehensive survey of tools for visualizing time series data in general (not restricted to the categorical case) is provided by Aigner et al. (2011).
or of sets of such tuples. A comprehensive survey of tools for visualizing time series data in general (not restricted to the categorical case) is provided by Aigner et al. (2011).

Figure 6.3 Spectral envelope of wood pewee data; see Remark 6.1.3.
6.2 Marginal Properties of Categorical Time Series
Let ![]() be a stationary categorical process with marginal distribution
be a stationary categorical process with marginal distribution ![]() . Given the segment
. Given the segment ![]() from this process, we estimate
from this process, we estimate ![]() by the vector
by the vector ![]() of relative frequencies computed from
of relative frequencies computed from ![]() , which is also expressed as
, which is also expressed as ![]() by using the above binarization of the process. Especially if
by using the above binarization of the process. Especially if ![]() is large, the complete (estimated) marginal distribution might be difficult to interpret. So, as with real-valued data, it is necessary in practice to reduce the full information about the marginal distribution into a few metrics that concentrate on features such as location and dispersion.
is large, the complete (estimated) marginal distribution might be difficult to interpret. So, as with real-valued data, it is necessary in practice to reduce the full information about the marginal distribution into a few metrics that concentrate on features such as location and dispersion.
Measuring the location of a categorical random variable ![]() (or to estimate it from
(or to estimate it from ![]() ) is rather straightforward; see also Examples 6.1.1 and 6.1.2. In any case, it is possible to compute “the” (sample) mode, although such a mode is sometimes not uniquely determined. If
) is rather straightforward; see also Examples 6.1.1 and 6.1.2. In any case, it is possible to compute “the” (sample) mode, although such a mode is sometimes not uniquely determined. If ![]() is even ordinal, then the median (or any other quantile) can be used to express the “center” of
is even ordinal, then the median (or any other quantile) can be used to express the “center” of ![]() or
or ![]() , respectively.
, respectively.
Categorical dispersion is not that obvious in the beginning. Even in the ordinal case, a quantile-based dispersion measure such as the inter quartile range (IQR) is not applicable, since a difference between categories is not defined (one might use the number of categories between the quartiles as a substitute). Therefore, let us first think about the intuitive meaning of dispersion. For a real-valued random variable ![]() , measures such as variance or IQR ultimately aim at expressing uncertainty. The smaller the dispersion of
, measures such as variance or IQR ultimately aim at expressing uncertainty. The smaller the dispersion of ![]() , the better we can predict the outcome of
, the better we can predict the outcome of ![]() . Adapting this intuitive understanding of dispersion to the categorical case, we have maximal dispersion if all probabilities
. Adapting this intuitive understanding of dispersion to the categorical case, we have maximal dispersion if all probabilities ![]() are equal to each other, because then, every outcome is equally probable and a reasonable prediction is impossible. So a uniform distribution in
are equal to each other, because then, every outcome is equally probable and a reasonable prediction is impossible. So a uniform distribution in ![]() constitutes one extreme of categorical dispersion. At the other extreme, if
constitutes one extreme of categorical dispersion. At the other extreme, if ![]() for one
for one ![]() and 0 otherwise (one-point distribution, so
and 0 otherwise (one-point distribution, so ![]() equals one of the unit vectors
equals one of the unit vectors ![]() ), then we are able to perfectly predict the outcome of
), then we are able to perfectly predict the outcome of ![]() , so
, so ![]() has minimal dispersion in this sense.
has minimal dispersion in this sense.
Now that the extremes of categorical dispersion are known, we can think of dispersion measures ![]() that map these extremes at the extremes of their range. In fact, several measures for this purpose are readily available in the literature; see the survey in Appendix A of Weiß & Göb (2008), for instance. Furthermore, any concentration index can be used as a measure of dispersion.
that map these extremes at the extremes of their range. In fact, several measures for this purpose are readily available in the literature; see the survey in Appendix A of Weiß & Göb (2008), for instance. Furthermore, any concentration index can be used as a measure of dispersion.
For the sake of simplicity, we consider measures ![]() with range
with range ![]() , where 0 refers to minimal dispersion, and 1 to maximal dispersion. Two popular (and, in the author's opinion, quite useful) measures of categorical dispersion are the Gini index and entropy. We define the (sample) Gini index as
, where 0 refers to minimal dispersion, and 1 to maximal dispersion. Two popular (and, in the author's opinion, quite useful) measures of categorical dispersion are the Gini index and entropy. We define the (sample) Gini index as
respectively. The theoretical Gini index ![]() has range
has range ![]() , where increasing values indicate increasing dispersion, with the extremes
, where increasing values indicate increasing dispersion, with the extremes ![]() iff
iff ![]() has a one-point distribution, and
has a one-point distribution, and ![]() iff
iff ![]() has a uniform distribution. The sample Gini index
has a uniform distribution. The sample Gini index ![]() is asymptotically normally distributed in the i.i.d. case, and the variance is approximated by
is asymptotically normally distributed in the i.i.d. case, and the variance is approximated by 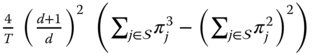 . Furthermore, although it is a biased estimator of
. Furthermore, although it is a biased estimator of ![]() , its bias is easily corrected in the i.i.d. case by considering
, its bias is easily corrected in the i.i.d. case by considering ![]() instead (Weiß, 2011a).
instead (Weiß, 2011a).
As an alternative, we define the (sample) entropy as

respectively, where we always use the convention ![]() .
. ![]() has the same properties as mentioned for the theoretical Gini index. In the i.i.d. case,
has the same properties as mentioned for the theoretical Gini index. In the i.i.d. case, ![]() is also asymptotically normally distributed, now with approximate variance
is also asymptotically normally distributed, now with approximate variance ![]() , but there is no simple way to exactly correct the bias of
, but there is no simple way to exactly correct the bias of ![]() (Weiß, 2013b).
(Weiß, 2013b).
If we would like to do a bias correction or compute confidence intervals for the dispersion measures in Example 6.2.2, we would first need to further investigate the serial dependence structure of the available time series, say to establish a possible i.i.d.-behavior such that the above asymptotics could be used. Corresponding tools for measuring serial dependence are presented in the next section.
6.3 Serial Dependence of Categorical Time Series
For the count time series considered in Part I, we simply used the well-known autocorrelation function to analyze the serial dependence structure; see Section 2.4. But this function is not defined in the categorical case (neither nominal nor ordinal), so different approaches are required. Before presenting particular measures, let us again start with some more general thoughts. As for the autocorrelation function, we shall look at pairs ![]() with
with ![]() from the underlying stationary categorical process. If, after having observed
from the underlying stationary categorical process. If, after having observed ![]() , it is possible to perfectly predict
, it is possible to perfectly predict ![]() , then it would be plausible to refer to
, then it would be plausible to refer to ![]() and
and ![]() as perfectly dependent. If, in contrast, knowledge about
as perfectly dependent. If, in contrast, knowledge about ![]() would not help in these respects, then
would not help in these respects, then ![]() and
and ![]() would seem to be independent.
would seem to be independent.
To translate this intuition into formulae, let us introduce the notation ![]() with
with ![]() for the lagged bivariate probabilities, with the sample counterpart
for the lagged bivariate probabilities, with the sample counterpart ![]() being the relative frequency of
being the relative frequency of ![]() within the pairs
within the pairs ![]() . Using the binarization, we can express the latter as
. Using the binarization, we can express the latter as ![]() ; that is,
; that is, ![]() . The corresponding conditional bivariate probabilities are denoted as
. The corresponding conditional bivariate probabilities are denoted as ![]() for
for ![]() ; see also Appendix B.2. To avoid computational difficulties, we assume that all marginal probabilities are truly positive (
; see also Appendix B.2. To avoid computational difficulties, we assume that all marginal probabilities are truly positive (![]() for all
for all ![]() ); otherwise, we would first have to reduce the state space.
); otherwise, we would first have to reduce the state space.
Following Weiß & Göb (2008), we now say that:
- we have perfect (unsigned) serial dependence at lag
 iff for any
iff for any  , the conditional distribution
, the conditional distribution  is a one-point distribution
is a one-point distribution - we have perfect serial independence at lag
 iff
iff  for any
for any  (or, equivalently, if
(or, equivalently, if 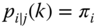 ).
).
The term “unsigned” was used above for the following reason: the autocorrelation function may take positive or negative values, hence being a signed measure, and positive autocorrelation implies, amongst other things, that large values tend to be followed by large values (and vice versa). This motivates us to introduce an analogous concept of signed categorical dependence, where positive dependence implies that the process tends to stay in the state it has reached (and vice versa). So again following Weiß & Göb (2008), and given that we have already established perfect serial dependence at lag ![]() (in the unsigned sense above), we now say that
(in the unsigned sense above), we now say that
- we even have perfect positive serial dependence iff all
 , or
, or - we even have perfect negative serial dependence iff all
 .
.
The latter implies that ![]() necessarily has to take a state other than
necessarily has to take a state other than ![]() . A number of measures of unsigned serial dependence have been proposed in the literature so far (Dehnert et al., 2003; Weiß & Göb, 2008; Biswas & Song, 2009; Weiß, 2013b). We shall consider one such measure here, namely Cramer's
. A number of measures of unsigned serial dependence have been proposed in the literature so far (Dehnert et al., 2003; Weiß & Göb, 2008; Biswas & Song, 2009; Weiß, 2013b). We shall consider one such measure here, namely Cramer's ![]() , where the selection is motivated by the attractive properties of the theoretical
, where the selection is motivated by the attractive properties of the theoretical ![]() as well as of the sample version
as well as of the sample version ![]() of this measure. It is defined by
of this measure. It is defined by
![]() has the range
has the range ![]() , where the boundaries 0 and 1 are reached iff we have perfect serial independence/dependence at lag
, where the boundaries 0 and 1 are reached iff we have perfect serial independence/dependence at lag ![]() . The distribution of its sample counterpart
. The distribution of its sample counterpart ![]() , in the case of an underlying i.i.d. process, is asymptotically approximated by a
, in the case of an underlying i.i.d. process, is asymptotically approximated by a ![]() -distribution (Weiß, 2013b):
-distribution (Weiß, 2013b): ![]() .
.
This relationship is quite useful in practice, since it allows us to uncover significant serial dependence. If the null of serial independence at lag ![]() is to be tested on (approximate) level
is to be tested on (approximate) level ![]() , and if
, and if ![]() denotes the
denotes the ![]() -quantile of the
-quantile of the ![]() -distribution, then we will reject the null if
-distribution, then we will reject the null if ![]() . This critical value can also be plotted into a graph of
. This critical value can also be plotted into a graph of ![]() against
against ![]() , as a substitute for the ACF plot familiar from real-valued time series analysis; see also Remark 2.3.1. On the other hand, this asymptotic result also shows that
, as a substitute for the ACF plot familiar from real-valued time series analysis; see also Remark 2.3.1. On the other hand, this asymptotic result also shows that ![]() is generally a biased estimator of
is generally a biased estimator of ![]() .
.
As a measure of signed serial dependence, we consider the (sample) Cohen's ![]()

The range of ![]() is given by
is given by ![]() , where 0 corresponds to serial independence, with positive (negative) values indicating positive (negative) serial dependence at lag
, where 0 corresponds to serial independence, with positive (negative) values indicating positive (negative) serial dependence at lag ![]() . For the i.i.d. case, Weiß (2011a) showed that
. For the i.i.d. case, Weiß (2011a) showed that ![]() is asymptotically normally distributed, with approximate mean
is asymptotically normally distributed, with approximate mean ![]() and variance
and variance ![]() . So there is only a small negative bias, which is easily corrected by adding
. So there is only a small negative bias, which is easily corrected by adding ![]() to
to ![]() , and the asymptotic result can again be applied to test for significant dependence.
, and the asymptotic result can again be applied to test for significant dependence.

Figure 6.4 Serial dependence plots of wood pewee data based on (a) Cramer's 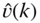 , (b) Cohen's
, (b) Cohen's  . See Example 6.3.1.
. See Example 6.3.1.
Table 6.3 Partial Cramer's ![]() and partial Cohen's
and partial Cohen's ![]() for wood pewee data
for wood pewee data
| k | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 0.626 | 0.665 | −0.207 | 0.315 | 0.053 | −0.027 | 0.024 | |
| −0.542 | −0.157 | −0.564 | 0.431 | 0.143 | 0.137 | −0.041 |
For completeness, the serial dependence plots for the EEG sleep state data (Example 6.1.1) are also shown, in Figure 6.5, although these data are even ordinal. This specific application illustrates a possible issue with Cramer's ![]() : for short time series (here, we have
: for short time series (here, we have ![]() ), it may be that some states are not observed (the state ‘aw’ in this case). To circumvent division by zero when computing (6.3), all summands related to ‘aw’ have been dropped while computing
), it may be that some states are not observed (the state ‘aw’ in this case). To circumvent division by zero when computing (6.3), all summands related to ‘aw’ have been dropped while computing ![]() . The dependence measure
. The dependence measure ![]() , in contrast, is robust with respect to zero frequencies.
, in contrast, is robust with respect to zero frequencies.

Figure 6.5 Serial dependence plots of EEG sleep state data, based on (a) Cramer's  , (b) Cohen's
, (b) Cohen's  ; see Example 6.1.1.
; see Example 6.1.1.
Let us conclude this section with the special case of a binary process (that is, ![]() ). If the range of
). If the range of ![]() is coded by 0 and 1, then a quantitative interpretation is possible, since each
is coded by 0 and 1, then a quantitative interpretation is possible, since each ![]() then simply follows a Bernoulli distribution with
then simply follows a Bernoulli distribution with ![]() and
and ![]() ; see Example A.2.1.
; see Example A.2.1.


