Chapter 10
Integration for Experts
IN THIS CHAPTER
Breaking down integrals into parts
Finding trigonometric integrals
Understanding the As, Bs, and Cxs of partial fractions
I figure it wouldn’t hurt to give you a break from the kind of theoretical groundwork stuff that I lay on pretty thick in Chapter 9, so this chapter cuts to the chase and shows you just the nuts and bolts of several integration techniques.
Integration by Parts
The basic idea of integration by parts is to transform an integral you can’t do into a simple product minus an integral you can do. Here’s the formula:
Integration by Parts: 
And here’s the method in a nutshell. What’s 
? First, you’ve got to split up the integrand into a u and a dv so that it fits the formula. For this problem, choose 
to be your u. Then everything else is the dv, namely 
. (I show you how to choose u in the next section.) Next, you differentiate u to get your du, and you integrate dv to get your v. Finally, you plug everything into the formula and you’re home free.
To help keep everything straight, organize integration-by-parts problems with a box like the one on the left in Figure 10-1. For each new problem, draw an empty 2-by-2 box, then put your u in the upper-left corner and your dv in the lower-right corner. The box for the above problem is on the right in Figure 10-1.
FIGURE 10-1: The integration-by-parts box.
The arrows in Figure 10-1 remind you to differentiate on the left and to integrate on the right. Now do the calculus and complete the box as shown in Figure 10-2:
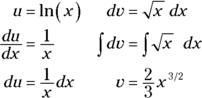
FIGURE 10-2: The completed box for 
.
Ready to finish? Plug everything into the formula:
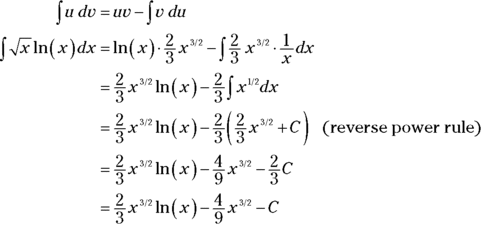
In the last step, you replace the 
with C because 
times any old number is still just any old number.
Picking your u
Here’s a great mnemonic for how to choose the u (again, once you’ve picked your u, everything else is the dv).
Herbert E. Kasube came up with the acronym LIATE to help you choose your u (calculus nerds can check out Herb’s article in the American Mathematical Monthly 90, 1983 issue):
L |
Logarithmic |
(like log(x)) |
I |
Inverse trigonometric |
(like arctan(x)) |
A |
Algebraic |
(like |
T |
Trigonometric |
(like cos(x)) |
E |
Exponential |
(like |
)
)To pick your u, go down this list; the first type of function on it that appears in the integrand is the u. Example: Integrate 
. (Integration by parts sometimes works for integrands like this one that contain only a single function.)
-
Go down the LIATE list and pick the u.
You see that there are no logarithmic functions in
, but there is an inverse trigonometric function,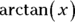 
. So that’s your u. Everything else is your dv, namely, plain old dx. - Do the box thing. See Figure 10-3.
- Plug everything into the integration-by-parts formula.
Now you can finish this problem by integrating
with the substitution method, setting 
. Try it. Note that the u in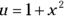 
has nothing to do with integration-by-parts u. Your final answer should be 
.
FIGURE 10-3: The box thing.
Here’s another one. Integrate 
.
-
Go down the LIATE list and pick the u.
Going down the LIATE list, the first type of function you find in
is a very simple algebraic one, namely x, so that’s your u. - Do the box thing. See Figure 10-4.
- Plug everything into the integration-by-parts formula.
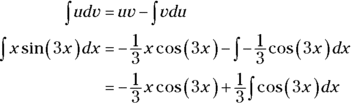
You can easily integrate
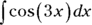with substitution or the guess-and-check method. Your final answer should be 
.
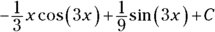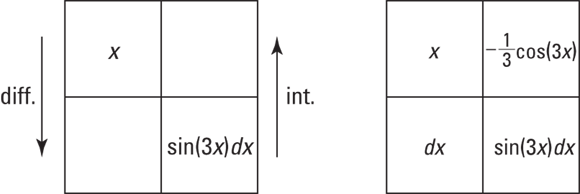
FIGURE 10-4: Yet more boxes.
Tricky Trig Integrals
In this section, you integrate powers of the six trigonometric functions, like 
and 
, and products or quotients of trig functions, like 
and 
. This is a bit tedious — time for some caffeine. To use the following techniques, you must have an integrand that contains just one of the six trig functions like 
or a certain pairing of trig functions, like 
. If the integrand has two trig functions, the two must be one of these three pairs: sine with cosine, secant with tangent, or cosecant with cotangent. For an integrand containing something other than one of these pairs, you can convert the problem into one of these pairs by using trig identities like 
and 
. For instance,
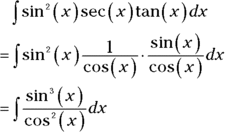
After any needed conversions, you get one of three cases:
where either m or n is a positive integer.
Positive powers of trig functions are generally preferable to negative powers, so, for example, you want to convert 
into 
.
Sines and cosines
This section covers integrals containing sines and cosines.
Case 1: The power of sine is odd and positive
If the power of sine is odd and positive, lop off one sine factor and put it to the right of the rest of the expression, convert the remaining sine factors to cosines with the Pythagorean identity, and then integrate with the substitution method where 
.
The Pythagorean identity tells you that, for any angle x, 
. And thus 
and 
.
Now integrate 
.
- Lop off one sine factor and move it to the right.
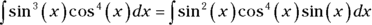
- Convert the remaining sines to cosines using the Pythagorean identity and simplify.
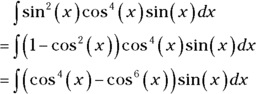
- Integrate with substitution, where
. 
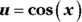You can save a little time in all substitution problems by just solving for du — as I did immediately above — and not bothering to solve for dx. You then tweak the integral so that it contains the thing du equals (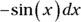
) in this problem. The integral contains a 
, so you multiply it by 
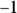to turn it into 
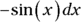and then compensate for that 
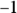by multiplying the whole integral by 
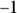. This is a wash because 
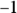times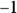 
equals 1. This may not sound like much of a shortcut, but it’s a good time-saver once you get used to it.So tweak your integral:
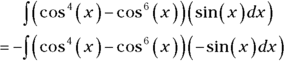
Now substitute and solve by the reverse power rule:
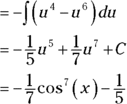
Case 2: The power of cosine is odd and positive
This problem works exactly like Case 1, except that the roles
of sine and cosine are reversed. Find 
.
- Lop off one cosine factor and move it to the right.
- Convert the remaining cosines to sines with the Pythagorean identity and simplify.
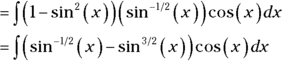
- Integrate with substitution, where
. 
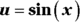Now substitute:
And finish integrating as in Case 1.
Case 3: The powers of both sine and cosine are even and nonnegative
Here you convert the integrand into odd powers of cosines by using the following trig identities:
and 
Then you finish the problem as in Case 2. Here’s an example:
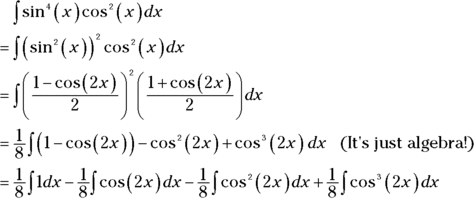
The first in this string of integrals is a no-brainer; the second is a simple reverse rule with a little tweak for the 2; you do the third integral by using the 
identity a second time; and the fourth integral is handled by following the steps in Case 2. Do it. Your final answer should be
Secants and tangents
This section covers integrals — are you sitting down? — containing secants and tangents!
Case 1: The power of tangent is odd and positive
Integrate 
.
-
Lop off a secant-tangent factor and move it to the right.
First, rewrite the problem:
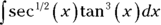.Taking a secant-tangent factor out of
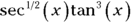may seem like squeezing blood from a turnip because 
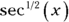has a power less than 
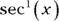, but it works: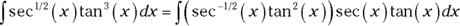 
-
Convert the remaining tangents to secants with the tangent-secant version of the Pythagorean identity.
The Pythagorean identity is
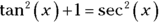, and thus 
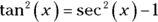. Now make the switch.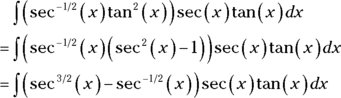 
- Solve by substitution with
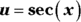and 
. 
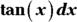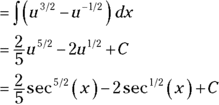
Case 2: The power of secant is even and positive
Find 
.
- Lop off a
factor and move it to the right. 
- Convert the remaining secants to tangents with the Pythagorean identity,
.
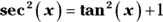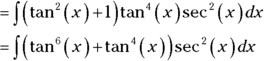
- Solve by substitution, where
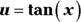and 
. 
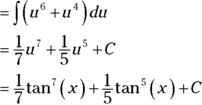
Case 3: The power of tangent is even and positive and there are no secant factors
Integrate 
.
- Convert one
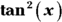factor to secants using the Pythagorean identity, 
. 
- Distribute and split up the integral.
-
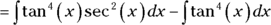
Solve the first integral like in Step 3 of Case 2 for secants and tangents.
You should get
. -
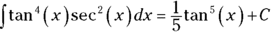For the second integral from Step 2, go back to Step 1 and repeat the process.
For this piece of the problem, you get
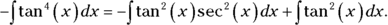
- Repeat Step 3 for
(using Case 2, Step 3) for secants and tangents again).
-
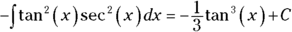
Use the Pythagorean identity to convert the
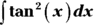from Step 4 into 
.Both of these integrals can be done with simple reverse differentiation rules. After collecting all these pieces — piece 1 from Step 3, piece 2 from Step 5, and pieces 3 and 4 from Step 6 — your final answer should be
.
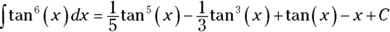Cosecants and cotangents
Cosecant and cotangent integrals work exactly like the three cases for secants and tangents — you just use a different form of the Pythagorean identity: 
. Try this one: Integrate 
. If you get 
, pass “Go” and collect $200.
If you get a secant-tangent or a cosecant-cotangent problem that doesn’t fit any of the cases discussed in the previous section or if you’re otherwise stumped by a problem, try converting it to sines and cosines and solving it with one of the sine-cosine methods or with identities like 
and 
.
Trigonometric Substitution
With the trigonometric substitution method, you can do integrals containing radicals of the following forms: 
, 
, and 
(as well as powers of those roots), where a is a constant and u is an expression containing x. For instance, 
is of the form 
.
I’ve got some silly mnemonic tricks to help you keep the three cases of this method straight. (Remember, with mnemonic devices, silly works.) First, the three cases involve three trig functions, tangent, sine, and secant. Their initial letters, t, s, and s, are the same letters as the initial letters of the name of this technique, trigonometric substitution. Pretty nice, eh?
Table 10-1 shows how these three trig functions pair up with the radical forms listed in the opening paragraph.
TABLE 10-1 A Totally Radical Table
|
|
|
|
|
|
|
|
To keep these pairings straight, note that the plus sign in 
looks like a little t for tangent, and that the other two forms, 
and 
, contain a subtraction sign — s is for sine and secant. To memorize what sine and secant pair up with, note that 
begins with the letter a, and it’s a sin to call someone an ass. Okay, I admit this is pretty weak. If you can come up with a better mnemonic, use it!
Case 1: Tangents
Find 
. First, note that this can be rewritten as 
, so it fits the form 
, where 
and 
.
-
Draw a right triangle — basically a SohCahToa triangle — where
equals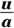 
, which is 
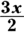.Because you know that
(from SohCahToa), your triangle should have 3x as O, the side opposite the angle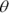 
, and 2 as A, the adjacent side. Then, by the Pythagorean Theorem, the length of the hypotenuse automatically equals your radical, 
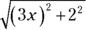, or 
. See Figure 10-5. - Solve
for x, differentiate, and solve for dx.
-
Find which trig function is represented by the radical over the a and then solve for the radical.
Look at the triangle in Figure 10-5. The radical is the hypotenuse and a is 2, the adjacent side, so
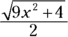is 
, which equals secant. So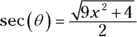 
, and thus 
. -
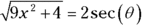Use the results from Steps 2 and 3 to make substitutions in the original problem, then integrate.
From Steps 2 and 3 you have
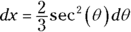and 
. Now you can finally do the integration.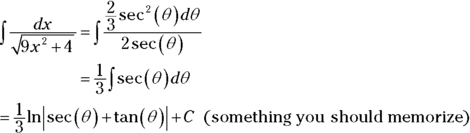 
- Substitute the x expressions from Steps 1 and 3 back in for
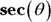and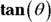 
. You can also get the expressions from the triangle in Figure 10-5.
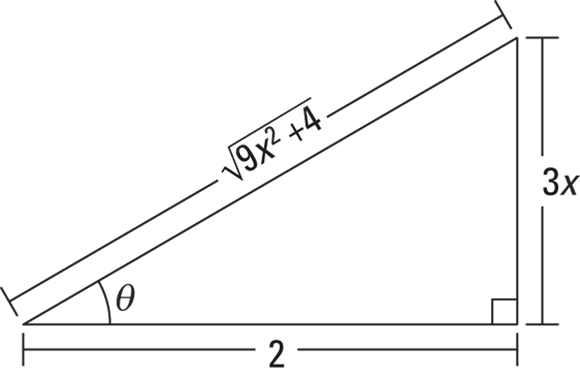
FIGURE 10-5: A SohCahToa triangle for the 
case.
For all three cases in trigonometric substitution, Step 1 always involves drawing a triangle in which the trig function in question equals 
:
For all three cases, Step 3 always involves putting the radical over the a. The three cases are given below, but you don’t need to memorize the trig functions in this list because you’ll know which one you’ve got by just looking at the triangle—assuming you know SohCahToa and the reciprocal trig functions. I’ve left out what goes under the radicals because by the time you’re doing Step 3, you’ve already got the right radical expression.
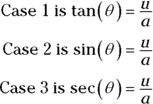
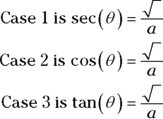
Just remember 
for Step 1 and 
for Step 3.
Case 2: Sines
Integrate 
, rewriting it first as 
so that it fits the form 
, where 
and 
.
-
Draw a right triangle where
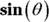, which is 
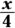.Sine equals
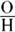, so the opposite side is x and the hypotenuse is 4. The length of the adjacent side is then automatically equal to your radical, 
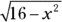. See Figure 10-6. - Solve
for x, differentiate, and solve for dx.
-
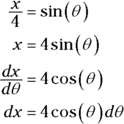
Find which trig function equals the radical over the a, and then solve for the radical.
Look at the triangle in Figure 10-6. The radical,
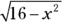, over the a, 4, is 
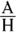, which you know from SohCahToa equals cosine. So that gives you 
-
Use the results from Steps 2 and 3 to make substitutions in the original problem, then integrate.
Note that in this particular problem, you have to make three substitutions, not just two like in the first example. From Steps 2 and 3 you’ve got
, 
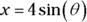, and 
, so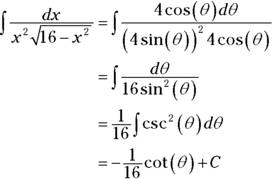 
- The triangle shows that
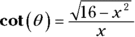. Substitute back for your final answer.
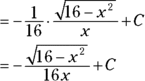
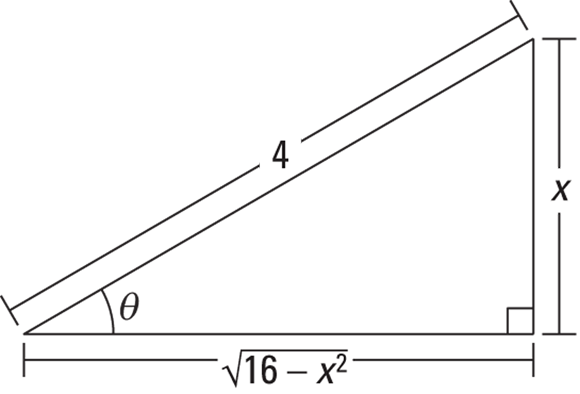
FIGURE 10-6: A SohCahToa triangle for the 
case.
Case 3: Secants
In the interest of space — and sanity — let’s skip this case. But you won’t have any trouble with it, because all the steps are basically the same as in Cases 1 and 2. Try this one.
Integrate 
. I’ll get you started. In Step 1, you draw a triangle, where 
, that’s 
. Now take it from there. You should get: 
.
Partial Fractions
You use the partial fractions method to integrate rational functions like 
. The basic idea involves “unadding” a fraction. Adding works like this: 
. So you can “unadd” 
by splitting it up into 
plus 
. This is what you do with the partial fraction technique except that you do it with complicated rational functions instead of ordinary fractions.
Case 1: The denominator contains only linear factors
Integrate 
. This is Case 1 because the factored denominator (see Step 1) contains only linear factors.
- Factor the denominator.
- Break up the fraction on the right into a sum of fractions, where each factor of the denominator in Step 1 becomes the denominator of a separate fraction. Then put unknowns in the numerator of each fraction.
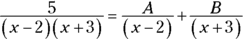
- Multiply both sides of this equation by the denominator of the left side.
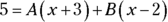
- Take the roots of the linear factors and plug them — one at a time — into x in the equation from Step 3, and solve for the unknowns.
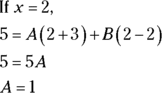
- Plug these results into the A and B in the equation from Step 2.
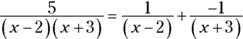
- Split up the original integral into the partial fractions from Step 5 and you’re home free.
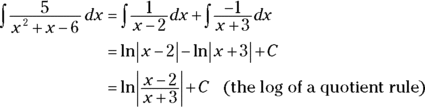
Case 2: The denominator contains unfactorable quadratic factors
Sometimes you can’t factor a denominator all the way down to linear factors because some quadratics can’t be factored.
Here’s a problem: Integrate 
.
-
Factor the denominator.
It’s already done! Note that
can’t be factored. -
Break up the fraction into a sum of “partial fractions.”
If you have an irreducible quadratic factor (like the
), the numerator for that partial fraction needs two unknowns in the form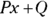 
. 
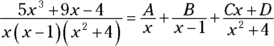
- Multiply both sides of this equation by the left-side denominator.
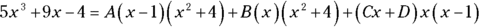
- Take the roots of the linear factors and plug them — one at a time — into x in the equation from Step 3, and then solve.
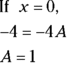
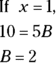
Unlike in the Case 1 example, you can’t solve for all the unknowns by plugging in the roots of the linear factors, so you have more work to do.
- Plug into the Step 3 equation the known values of A and B and any two values for x not used in Step 4 to get a system of two equations in C and D.
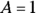and 
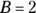, so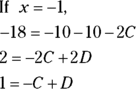
-
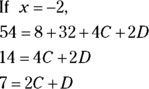
Solve the system:
and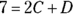 
.You should get
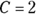and 
. -
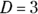Split up the original integral and integrate.
Using the values obtained in Steps 4 and 6,
, 
, 
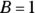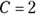, and 
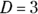, and the equation from Step 2, you can split up the original integral into three pieces: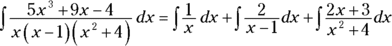 
And with basic algebra, you can split up the third integral on the right into two pieces, resulting in the final partial fraction decomposition:
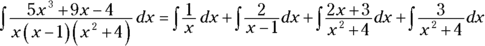
The first two integrals are easy. For the third, you use substitution with
and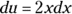 
. The fourth is done with the arctangent rule which you should memorize: 
.
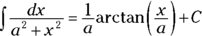Case 3: The denominator contains repeated factors
If the denominator contains any repeated factors (linear or quadratic), like 
, here’s what you do: Say you want to integrate 
. The x in the denominator has a power of 2, so you get 2 partial fractions for the x (for the powers of 1 and 2); the 
has a power of 3, so you get 3 partial fractions for that factor (for the powers 1, 2, and 3). Here’s the general form for the partial fraction decomposition: 
. Here’s another one. You break up 
into 
. I’m skipping the solutions for these examples. The method’s the same as in Cases 1 and 2 above — just messier.
Equating coefficients
Here’s another method for finding your capital letter unknowns that you should have in your bag of tricks. Say you get the following for your Step 3 equation:
This equation has no linear factors, so you can’t plug in the roots to get the unknowns. Instead, expand the right side of the equation:
And collect like terms:
Then equate the coefficients of like terms from the left and right sides of the equation:
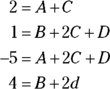
You then solve this system of simultaneous equations to get A, B, C, and D.
In a nutshell, you have three ways to find your A, B, C, etc.: 1) Plugging in the roots of the linear factors of the denominator if there are any, 2) Plugging in other values of x and solving the resulting system of equations, and 3) Equating the coefficients of like terms. With practice, you’ll get good at combining these methods to find your unknowns quickly.