Chapter 3
Evaluating Limits
IN THIS CHAPTER
![]() Solving limits with algebra
Solving limits with algebra
![]() Finding limits at infinity
Finding limits at infinity
Chapter 2 introduces the concept of a limit. This chapter gets down to the nitty-gritty and presents several techniques for calculating the answers to limit problems.
Easy Limits
A few limit problems are very easy.
Limits to memorize
You should memorize the following limits. If you fail to memorize the last three, you’ll waste a lot of time trying to figure them out.
-
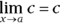
(
 is a horizontal line, so the limit — which is the function height — must equal c regardless of the x-number.)
is a horizontal line, so the limit — which is the function height — must equal c regardless of the x-number.) 
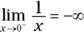
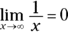
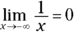
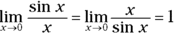


Plug-and-chug limits
Plug-and-chug problems make up the second category of easy limits. Just plug the x-number into the limit function, and if the computation results in a number, that’s your answer. For example,
This method works for limits involving continuous functions and functions that are continuous over their entire domains. These are well-duh limit problems, and, to be perfectly frank, there’s really no point to them. The limit is simply the function value.
“Real” Limit Problems
If you plug the x-number into the limit expression and the result is undefined (usually ![]() ), you’ve got a “real” limit problem — and some work to do. In this chapter, you learn algebraic techniques for solving these “real” limit problems.
), you’ve got a “real” limit problem — and some work to do. In this chapter, you learn algebraic techniques for solving these “real” limit problems.
You use two main algebraic techniques for “real” limit problems: factoring and conjugate multiplication. I lump other algebra techniques in the section “Miscellaneous algebra.” All algebraic methods involve the same basic idea. When substitution doesn’t work in the original function — usually because of a hole in the function — you can use algebra to manipulate the function until substitution does work (it works because your manipulation plugs the hole).
Factoring
Here’s an example. Evaluate ![]() .
.
-
Try plugging 5 into x — you should always try substitution first.
You get
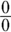 — no good, on to plan B.
— no good, on to plan B. 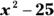 can be factored, so do it.
can be factored, so do it.

- Cancel the
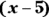 from the numerator and denominator.
from the numerator and denominator.

- Now substitution will work.

The function you got after canceling the ![]() , namely
, namely ![]() , is identical to the original function,
, is identical to the original function,![]() , except that the hole in the original function at (5, 10) has been plugged. Note that the limit as x approaches 5 is 10, which is the height of the hole at (5, 10).
, except that the hole in the original function at (5, 10) has been plugged. Note that the limit as x approaches 5 is 10, which is the height of the hole at (5, 10).
Conjugate multiplication
Try this method for fraction functions that contain square roots. Conjugate multiplication rationalizes the numerator or denominator of a fraction, which means getting rid of square roots. Try this one: Evaluate ![]() .
.
-
Try substitution.
Plug in 4: That gives you
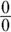 — time for plan B.
— time for plan B. -
Multiply the numerator and denominator by the conjugate of
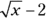 , which is
, which is  .
.Now do the rationalizing.
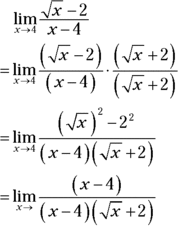
- Cancel the (x – 4) from the numerator and denominator.

- Now substitution works.

As with the factoring example, this rationalizing process plugged the hole in the original function. In this example, 4 is the x-number, ![]() is the answer, and the function
is the answer, and the function ![]() has a hole at
has a hole at ![]() .
.
Miscellaneous algebra
When factoring and conjugate multiplication don’t work, try other basic algebra like adding or subtracting fractions, multiplying or dividing fractions, canceling, or some other form of simplification.
Evaluate ![]() .
.
-
Try substitution.
Plug in 0: That gives you
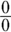 — no good.
— no good. -
Simplify the complex fraction (that’s a big fraction that contains little fractions) by multiplying the numerator and denominator by the least common denominator of the little fractions, namely
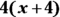 .
.Note: Adding or subtracting the little fractions in the numerator or denominator also works in this type of problem, but it’s a bit longer than the method here.
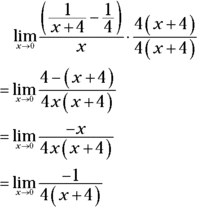
- Now substitution works.
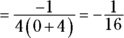
Limits at Infinity
In the limits in the last section, x approaches a finite number, but there are also limits where x approaches infinity or negative infinity. Consider the function ![]() . See Figure 3-1.
. See Figure 3-1.

FIGURE 3-1: The graph of 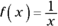 .
.
You can see on the graph (in the first quadrant) that as x gets bigger and bigger — in other words, as x approaches infinity — the height of the function gets lower and lower but never gets to zero. This is confirmed by considering what happens when you plug bigger and bigger numbers into ![]() . The outputs get smaller and smaller. This graph thus has a horizontal asymptote of
. The outputs get smaller and smaller. This graph thus has a horizontal asymptote of ![]() (the x-axis), and we say that
(the x-axis), and we say that ![]() . The fact that x never actually reaches infinity and that f never gets to zero has no relevance. When we say that
. The fact that x never actually reaches infinity and that f never gets to zero has no relevance. When we say that ![]() , we mean that as x gets bigger and bigger without end, f gets closer and closer to zero. The function f also approaches zero as x approaches negative infinity, written as
, we mean that as x gets bigger and bigger without end, f gets closer and closer to zero. The function f also approaches zero as x approaches negative infinity, written as ![]() .
.
Horizontal asymptotes
Horizontal asymptotes and limits at infinity go hand in hand — you can’t have one without the other. For a rational function like ![]() , determining the limit at infinity or negative infinity is the same as finding the location of the horizontal asymptote.
, determining the limit at infinity or negative infinity is the same as finding the location of the horizontal asymptote.
Here’s what you do. First, note the degree of the numerator (that’s the highest power of x in the numerator) and the degree of the denominator. You’ve got three cases:
- If the degree of the numerator is greater than the degree of the denominator, for example
 , there’s no horizontal asymptote and the limit of the function as x approaches infinity (or negative infinity) does not exist.
, there’s no horizontal asymptote and the limit of the function as x approaches infinity (or negative infinity) does not exist. - If the degree of the denominator is greater than the degree of the numerator, for example
 , the x-axis (the line
, the x-axis (the line 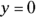 ) is the horizontal asymptote and
) is the horizontal asymptote and 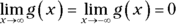 .
. - If the degrees of the numerator and denominator are equal, take the coefficient of the highest power of x in the numerator and divide it by the coefficient of the highest power of x in the denominator. That quotient gives you the answer to the limit problem and the height of the asymptote. For example, if
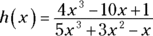
 , and h has a horizontal asymptote at
, and h has a horizontal asymptote at 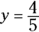 .
.
Solving limits at infinity
Let’s try some algebra for the problem ![]() .
.
-
Try substitution — always a good idea.
No good. You get
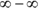 , which does not equal zero and which tells you nothing (see the related Warning in the previous section). On to plan B.
, which does not equal zero and which tells you nothing (see the related Warning in the previous section). On to plan B.Because
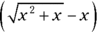 contains a square root, the conjugate multiplication method seems like a natural choice, except that that method is used for fraction functions. Well, just put
contains a square root, the conjugate multiplication method seems like a natural choice, except that that method is used for fraction functions. Well, just put 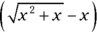 over the number 1 and, voilà, you’ve got a fraction:
over the number 1 and, voilà, you’ve got a fraction: 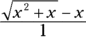 . Now do the conjugate multiplication.
. Now do the conjugate multiplication. - Multiply the numerator and denominator by the conjugate of
 and simplify.
and simplify.

- Now substitution does work.
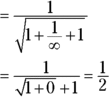

 The plug-and-chug method works for any type of function unless there’s a discontinuity at the x-number you plug in. In that case, the number you get after plugging in is not the limit. And if you plug the x-number into a limit like
The plug-and-chug method works for any type of function unless there’s a discontinuity at the x-number you plug in. In that case, the number you get after plugging in is not the limit. And if you plug the x-number into a limit like  Substitution doesn’t work for the problems in this section. If you try plugging into x in any of the rational functions in this section, you get
Substitution doesn’t work for the problems in this section. If you try plugging into x in any of the rational functions in this section, you get