Multiplication is another important binary operation on matrices. In the broader sense, the term matrix multiplication refers to several techniques that multiply matrices to produce a new matrix.

Let's define three matrices, A, B, and C, and a single value N, in the REPL. The matrices have the following values:

We can multiply the matrices by using the M/* function from the core.matrix library. Apart from being used to multiply two matrices, this function can also be used to multiply any number of matrices, and scalar values as well. We can try out the following M/* function to multiply two given matrices in the REPL:

user> (pm (M/* A B))
[[140.000 200.000]
 [320.000 470.000]]
nil
user> (pm (M/* A C))
RuntimeException Mismatched vector sizes  clojure.core.matrix.impl.persistent-vector/... 
user> (def N 10)
#'user/N
user> (pm (M/* A N))
[[10.000 20.000 30.000]
 [40.000 50.000 60.000]]
nil

First, we calculated the product of two matrices. This operation is termed as matrix-matrix multiplication. However, multiplying matrices A and C doesn't work, as the matrices have incompatible sizes. This brings us to the first rule of multiplying matrices: to multiply two matrices A and B, the number of columns in A have to be equal to the number of rows in B. The resultant matrix has the same number of rows as A and columns as B. That's the reason the REPL didn't agree to multiply A and C, but simply threw an exception.

For matrix A of size , and B of size , the product of the two matrices only exists if , and the product of A and B is a new matrix of size .

The product of matrices A and B is calculated by multiplying the elements of rows in A with the corresponding columns in B, and then adding the resulting values to produce a single value for each row in A and each column in B. Hence, the resulting product has the same number of rows as A and columns as B.

We can define the product of two matrices with compatible sizes as follows:

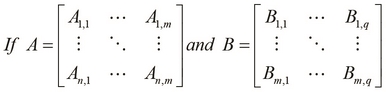
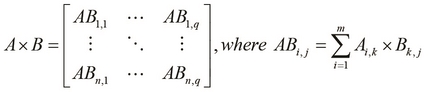
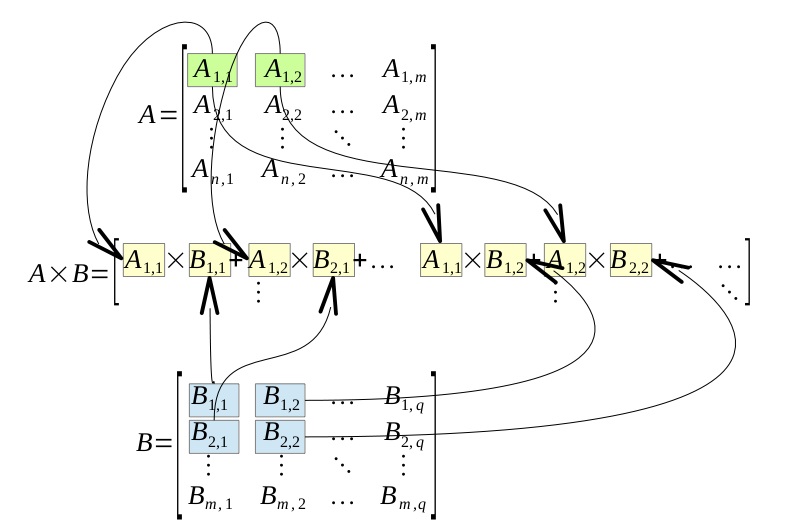
The following is an illustration of how the elements from A and B are used to calculate the product of the two matrices:

This does look slightly complicated, so let's demonstrate the preceding definition with an example, using the matrices A and B as we had previously defined. The following calculation does, in fact, agree to the value produced in the REPL:

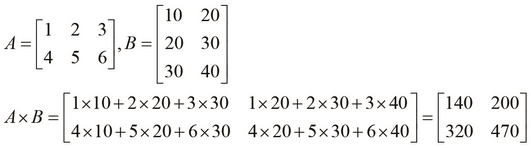
Note that multiplying matrices is not a commutative operation. However, the operation does exhibit the associative property of functions. For matrices A, B, and C of product-compatible sizes, the following properties are always true, with one exception that we will uncover later:

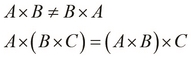
An obvious corollary is that a square matrix when multiplied with another square matrix of the same size produces a resultant matrix that has the same size as the two original matrices. Also, the square, cube, and other powers of a square matrix results in matrices of the same size.

Another interesting property of square matrices is that they have an identity element for multiplication, that is, an identity matrix of product-compatible size. But, an identity matrix is itself a square matrix, which brings us to the conclusion that the multiplication of a square matrix with an identity matrix is a commutative operation. Hence, the commutative rule for matrices, which states that matrix multiplication is not commutative, is actually not true when one of the matrices is an identity matrix and the other one is a square matrix. This can be formally summarized by the following equality:

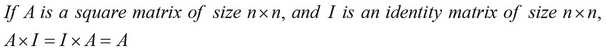
A naïve implementation of matrix multiplication would have a time complexity of , and requires eight multiplication operations for a matrix. By time complexity, we mean the time taken by a particular algorithm to run till completion. Hence, linear algebra libraries use more efficient algorithms, such as Strassen's algorithm, to implement matrix multiplication, which needs only seven multiplication operations and reduces the complexity to .

The clatrix library implementation for matrix multiplication performs significantly better than the default persistent vector implementation, since it interfaces with native libraries. In practice, we can use a benchmarking library such as criterium for Clojure (http://github.com/hugoduncan/criterium) to perform this comparison. Alternatively, we can also compare the performance of these two implementations in brief by defining a simple function to multiply two matrices and then passing large matrices of different implementations to it using our previously defined rand-square-mat and rand-square-clmat functions. We can define a function to measure the time taken to multiply two matrices.

Also, we can define two functions to multiply the matrices that were created using the rand-square-mat and rand-square-clmat functions that we previously defined, as follows:

(defn time-mat-mul
  "Measures the time for multiplication of two matrices A and B"
  [A B]
  (time (M/* A B)))

(defn core-matrix-mul-time []
  (let [A (rand-square-mat 100)
        B (rand-square-mat 100)]
    (time-mat-mul A B)))

(defn clatrix-mul-time []
  (let [A (rand-square-clmat 100)
        B (rand-square-clmat 100)]
    (time-mat-mul A B)))

We can see that the core.matrix implementation takes a second on average to compute the product of two randomly generated matrices. The clatrix implementation, however, takes less than a millisecond on average, although the first call that's made usually takes 35 to 40 ms to load the native BLAS library. Of course, this value could be slightly different depending on the hardware it's calculated on. Nevertheless, clatrix is preferred when dealing with large matrices unless there's a valid reason, such as hardware incompatibilities or the avoidance of an additional dependency, to avoid its usage.

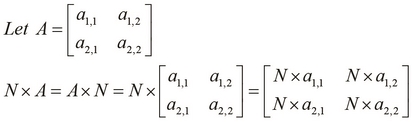
Next, let's look at scalar multiplication, which involves simply multiplying a single value N or a scalar with a matrix. The resultant matrix has the same size as the original matrix. For a 2 x 2 matrix, we can define scalar multiplication as follows:

For matrices and , the following is the product:

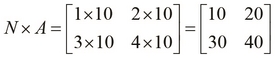
Note that we can also use the scale function from the core.matrix library to perform scalar multiplication:

user> (pm (scale A 10))
[[10.000 20.000 30.000]
 [40.000 50.000 60.000]]
nil
user> (M/== (scale A 10) (M/* A 10))
true

Finally, we will briefly take a look at a special form of matrix multiplication, termed as matrix-vector multiplication. A vector is simply a matrix with a single row, which on multiplication with a square matrix of product-compatible size produces a new vector with the same size as the original vector. After multiplying a matrix A of size and the transpose V' of a vector V, of size , a new vector V" of size is produced. If A is a square matrix, then V" has an identical size as that of the transpose V'.