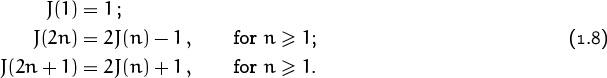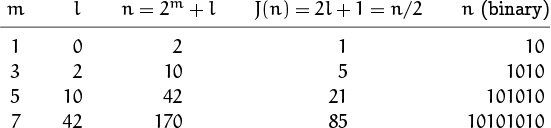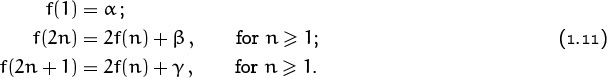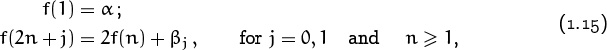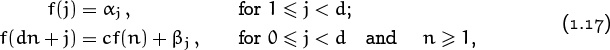1. Recurrent Problems

This chapter explores three sample problems that give a feel for what’s to come. They have two traits in common: They’ve all been investigated repeatedly by mathematicians; and their solutions all use the idea of recurrence, in which the solution to each problem depends on the solutions to smaller instances of the same problem.

1.1 The Tower of Hanoi

Let’s look first at a neat little puzzle called the Tower of Hanoi, invented by the French mathematician Edouard Lucas in 1883. We are given a tower of eight disks, initially stacked in decreasing size on one of three pegs:

Raise your hand if you’ve never seen this. OK, the rest of you can cut to equation (1.1).

The objective is to transfer the entire tower to one of the other pegs, moving only one disk at a time and never moving a larger one onto a smaller.

Gold—wow. Are our disks made of concrete?

Lucas [260] furnished his toy with a romantic legend about a much larger Tower of Brahma, which supposedly has 64 disks of pure gold resting on three diamond needles. At the beginning of time, he said, God placed these golden disks on the first needle and ordained that a group of priests should transfer them to the third, according to the rules above. The priests reportedly work day and night at their task. When they finish, the Tower will crumble and the world will end.

It’s not immediately obvious that the puzzle has a solution, but a little thought (or having seen the problem before) convinces us that it does. Now the question arises: What’s the best we can do? That is, how many moves are necessary and sufficient to perform the task?

The best way to tackle a question like this is to generalize it a bit. The Tower of Brahma has 64 disks and the Tower of Hanoi has 8; let’s consider what happens if there are n disks.

One advantage of this generalization is that we can scale the problem down even more. In fact, we’ll see repeatedly in this book that it’s advantageous to LOOK AT SMALL CASES first. It’s easy to see how to transfer a tower that contains only one or two disks. And a small amount of experimentation shows how to transfer a tower of three.

The next step in solving the problem is to introduce appropriate notation: NAME AND CONQUER. Let’s say that T_n is the minimum number of moves that will transfer n disks from one peg to another under Lucas’s rules. Then T₁ is obviously 1, and T₂ = 3.

We can also get another piece of data for free, by considering the smallest case of all: Clearly T₀ = 0, because no moves at all are needed to transfer a tower of n = 0 disks! Smart mathematicians are not ashamed to think small, because general patterns are easier to perceive when the extreme cases are well understood (even when they are trivial).

But now let’s change our perspective and try to think big; how can we transfer a large tower? Experiments with three disks show that the winning idea is to transfer the top two disks to the middle peg, then move the third, then bring the other two onto it. This gives us a clue for transferring n disks in general: We first transfer the n – 1 smallest to a different peg (requiring T_n–1 moves), then move the largest (requiring one move), and finally transfer the n–1 smallest back onto the largest (requiring another T_n–1 moves). Thus we can transfer n disks (for n > 0) in at most 2T_n–1 + 1 moves:

T_n ≤ 2T_n–1 + 1,          for n > 0.

This formula uses ‘≤’ instead of ‘ = ’ because our construction proves only that 2T_n–1 + 1 moves suffice; we haven’t shown that 2T_n–1 + 1 moves are necessary. A clever person might be able to think of a shortcut.

Most of the published “solutions” to Lucas’s problem, like the early one of Allardice and Fraser [7], fail to explain why T_n must be ≥ 2T_n–1 + 1.

But is there a better way? Actually no. At some point we must move the largest disk. When we do, the n – 1 smallest must be on a single peg, and it has taken at least T_n–1 moves to put them there. We might move the largest disk more than once, if we’re not too alert. But after moving the largest disk for the last time, we must transfer the n – 1 smallest disks (which must again be on a single peg) back onto the largest; this too requires T_n–1 moves. Hence

T_n ≥ 2T_n–1 + 1,          for n > 0.

These two inequalities, together with the trivial solution for n = 0, yield

(Notice that these formulas are consistent with the known values T₁ = 1 and T₂ = 3. Our experience with small cases has not only helped us to discover a general formula, it has also provided a convenient way to check that we haven’t made a foolish error. Such checks will be especially valuable when we get into more complicated maneuvers in later chapters.)

Yeah, yeah . . . I seen that word before.

A set of equalities like (1.1) is called a recurrence (a.k.a. recurrence relation or recursion relation). It gives a boundary value and an equation for the general value in terms of earlier ones. Sometimes we refer to the general equation alone as a recurrence, although technically it needs a boundary value to be complete.

The recurrence allows us to compute T_n for any n we like. But nobody really likes to compute from a recurrence, when n is large; it takes too long. The recurrence only gives indirect, local information. A solution to the recurrence would make us much happier. That is, we’d like a nice, neat, “closed form” for T_n that lets us compute it quickly, even for large n. With a closed form, we can understand what T_n really is.

So how do we solve a recurrence? One way is to guess the correct solution, then to prove that our guess is correct. And our best hope for guessing the solution is to look (again) at small cases. So we compute, successively, T₃ = 2·3 + 1 = 7; T₄ = 2·7 + 1 = 15; T₅ = 2·15 + 1 = 31; T₆ = 2·31 + 1 = 63. Aha! It certainly looks as if

At least this works for n ≤ 6.

Mathematical induction is a general way to prove that some statement about the integer n is true for all n ≥ n₀. First we prove the statement when n has its smallest value, n₀; this is called the basis. Then we prove the statement for n > n₀, assuming that it has already been proved for all values between n₀ and n – 1, inclusive; this is called the induction. Such a proof gives infinitely many results with only a finite amount of work.

Mathematical induction proves that we can climb as high as we like on a ladder, by proving that we can climb onto the bottom rung (the basis) and that from each rung we can climb up to the next one (the induction).

Recurrences are ideally set up for mathematical induction. In our case, for example, (1.2) follows easily from (1.1): The basis is trivial, since T₀ = 2⁰ − 1 = 0. And the induction follows for n > 0 if we assume that (1.2) holds when n is replaced by n − 1:

T_n = 2T_n–1 + 1 = 2(2^n–1 – 1) + 1 = 2ⁿ – 1.

Hence (1.2) holds for n as well. Good! Our quest for T_n has ended successfully.

Of course the priests’ task hasn’t ended; they’re still dutifully moving disks, and will be for a while, because for n = 64 there are 2⁶⁴–1 moves (about 18 quintillion). Even at the impossible rate of one move per microsecond, they will need more than 5000 centuries to transfer the Tower of Brahma. Lucas’s original puzzle is a bit more practical. It requires 2⁸ – 1 = 255 moves, which takes about four minutes for the quick of hand.

The Tower of Hanoi recurrence is typical of many that arise in applications of all kinds. In finding a closed-form expression for some quantity of interest like T_n we go through three stages:

1 Look at small cases. This gives us insight into the problem and helps us in stages 2 and 3.

2 Find and prove a mathematical expression for the quantity of interest. For the Tower of Hanoi, this is the recurrence (1.1) that allows us, given the inclination, to compute T_n for any n.

3 Find and prove a closed form for our mathematical expression. For the Tower of Hanoi, this is the recurrence solution (1.2).

What is a proof? “One half of one percent pure alcohol.”

The third stage is the one we will concentrate on throughout this book. In fact, we’ll frequently skip stages 1 and 2 entirely, because a mathematical expression will be given to us as a starting point. But even then, we’ll be getting into subproblems whose solutions will take us through all three stages.

Our analysis of the Tower of Hanoi led to the correct answer, but it required an “inductive leap”; we relied on a lucky guess about the answer. One of the main objectives of this book is to explain how a person can solve recurrences without being clairvoyant. For example, we’ll see that recurrence (1.1) can be simplified by adding 1 to both sides of the equations:

T₀ + 1 = 1;

T_n + 1 = 2T_n–1 + 2,          for n > 0.

Now if we let U_n = T_n + 1, we have

Interesting: We get rid of the +1 in (1.1) by adding, not by subtracting.

It doesn’t take genius to discover that the solution to this recurrence is just U_n = 2ⁿ; hence T_n = 2ⁿ – 1. Even a computer could discover this.

1.2 LINES IN THE PLANE

Our second sample problem has a more geometric flavor: How many slices of pizza can a person obtain by making n straight cuts with a pizza knife? Or, more academically: What is the maximum number L_n of regions defined by n lines in the plane? This problem was first solved in 1826, by the Swiss mathematician Jacob Steiner [338].

(A pizza with Swiss cheese?)

Again we start by looking at small cases, remembering to begin with the smallest of all. The plane with no lines has one region; with one line it has two regions; and with two lines it has four regions:

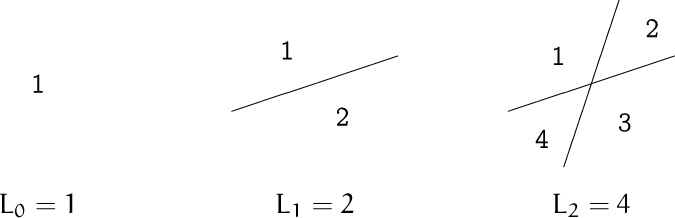
(Each line extends infinitely in both directions.)

Sure, we think, L_n = 2ⁿ; of course! Adding a new line simply doubles the number of regions. Unfortunately this is wrong. We could achieve the doubling if the nth line would split each old region in two; certainly it can split an old region in at most two pieces, since each old region is convex. (A straight line can split a convex region into at most two new regions, which will also be convex.) But when we add the third line—the thick one in the diagram below—we soon find that it can split at most three of the old regions, no matter how we’ve placed the first two lines:

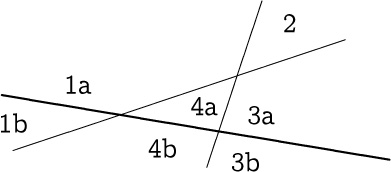
Thus L₃ = 4 + 3 = 7 is the best we can do.

A region is convex if it includes all line segments between any two of its points. (That’s not what my dictionary says, but it’s what mathematicians believe.)

And after some thought we realize the appropriate generalization. The nth line (for n > 0) increases the number of regions by k if and only if it splits k of the old regions, and it splits k old regions if and only if it hits the previous lines in k – 1 different places. Two lines can intersect in at most one point. Therefore the new line can intersect the n – 1 old lines in at most n – 1 different points, and we must have k ≤ n. We have established the upper bound

L_n ≤ L_n–1 + n,          for n > 0.

Furthermore it’s easy to show by induction that we can achieve equality in this formula. We simply place the nth line in such a way that it’s not parallel to any of the others (hence it intersects them all), and such that it doesn’t go through any of the existing intersection points (hence it intersects them all in different places). The recurrence is therefore

The known values of L₁, L₂, and L₃ check perfectly here, so we’ll buy this.

Now we need a closed-form solution. We could play the guessing game again, but 1, 2, 4, 7, 11, 16, . . . doesn’t look familiar; so let’s try another tack. We can often understand a recurrence by “unfolding” or “unwinding” it all the way to the end, as follows:

L_n = L_n–1 + n

= L_n–2 + (n – 1) + n

= L_n–3 + (n – 2) + (n – 1) + n

⋮

= L₀ + 1 + 2 + · · · + (n – 2) + (n – 1) + n

= 1   +   S_n ,          where S_n = 1 + 2 + 3 + · · · + (n – 1) + n.

Unfolding? I’d call this “plugging in.”

In other words, L_n is one more than the sum S_n of the first n positive integers.

The quantity S_n pops up now and again, so it’s worth making a table of small values. Then we might recognize such numbers more easily when we see them the next time:

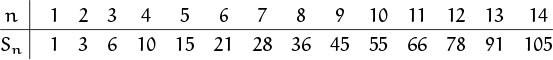
These values are also called the triangular numbers, because S_n is the number of bowling pins in an n-row triangular array. For example, the usual four-row array has S₄ = 10 pins.

To evaluate S_n we can use a trick that Gauss reportedly came up with in 1786, when he was nine years old [88] (and which had been used already by Archimedes in propositions 10 and 11 of his classic treatise on spirals):

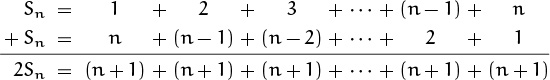
It seems a lot of stuff is attributed to Gauss—either he was really smart or he had a great press agent.

We merely add S_n to its reversal, so that each of the n columns on the right sums to n + 1. Simplifying,

Maybe he just had a magnetic personality.

OK, we have our solution:

Actually Gauss is often called the greatest mathematician of all time. So it’s nice to be able to understand at least one of his discoveries.

As experts, we might be satisfied with this derivation and consider it a proof, even though we waved our hands a bit when doing the unfolding and reflecting. But students of mathematics should be able to meet stricter standards; so it’s a good idea to construct a rigorous proof by induction. The key induction step is

L_n = L_n–1 + n = ((n – 1)n + 1) + n = n(n + 1) + 1.

Now there can be no doubt about the closed form (1.6).

When in doubt, look at the words. Why is it “closed,” as opposed to “open”? What image does it bring to mind?
Answer: The equation is “closed,” not defined in terms of itself—not leading to recurrence. The case is “closed”—it won’t happen again. Metaphors are the key.

Incidentally we’ve been talking about “closed forms” without explicitly saying what we mean. Usually it’s pretty clear. Recurrences like (1.1) and (1.4) are not in closed form—they express a quantity in terms of itself; but solutions like (1.2) and (1.6) are. Sums like 1 + 2 + · · · + n are not in closed form—they cheat by using ‘· · ·’; but expressions like n(n + 1)/2 are. We could give a rough definition like this: An expression for a quantity f(n) is in closed form if we can compute it using at most a fixed number of “well known” standard operations, independent of n. For example, 2ⁿ – 1 and n(n + 1)/2 are closed forms because they involve only addition, subtraction, multiplication, division, and exponentiation, in explicit ways.

The total number of simple closed forms is limited, and there are recurrences that don’t have simple closed forms. When such recurrences turn out to be important, because they arise repeatedly, we add new operations to our repertoire; this can greatly extend the range of problems solvable in “simple” closed form. For example, the product of the first n integers, n!, has proved to be so important that we now consider it a basic operation. The formula ‘n!’ is therefore in closed form, although its equivalent ‘1·2·. . .·n’ is not.

Is “zig” a technical term?

And now, briefly, a variation of the lines-in-the-plane problem: Suppose that instead of straight lines we use bent lines, each containing one “zig.” What is the maximum number Z_n of regions determined by n such bent lines in the plane? We might expect Z_n to be about twice as big as L_n, or maybe three times as big. Let’s see:

From these small cases, and after a little thought, we realize that a bent line is like two straight lines except that regions merge when the “two” lines don’t extend past their intersection point.

. . . and a little afterthought. . .

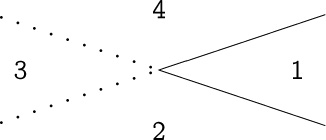
Regions 2, 3, and 4, which would be distinct with two lines, become a single region when there’s a bent line; we lose two regions. However, if we arrange things properly—the zig point must lie “beyond” the intersections with the other lines—that’s all we lose; that is, we lose only two regions per bent line. Thus

Exercise 18 has the details.

Comparing the closed forms (1.6) and (1.7), we find that for large n,

L_n ∼ n²,

Z_n ∼ 2n²;

so we get about four times as many regions with bent lines as with straight lines. (In later chapters we’ll be discussing how to analyze the approximate behavior of integer functions when n is large. The ‘∼’ symbol is defined in Section 9.1.)

1.3 The Josephus Problem

Our final introductory example is a variant of an ancient problem named for Flavius Josephus, a famous historian of the first century. Legend has it that Josephus wouldn’t have lived to become famous without his mathematical talents. During the Jewish–Roman war, he was among a band of 41 Jewish rebels trapped in a cave by the Romans. Preferring suicide to capture, the rebels decided to form a circle and, proceeding around it, to kill every third remaining person until no one was left. But Josephus, along with an unindicted co-conspirator, wanted none of this suicide nonsense; so he quickly calculated where he and his friend should stand in the vicious circle.

(Ahrens [5, vol. 2] and Herstein and Kaplansky [187] discuss the interesting history of this problem. Josephus himself [197] is a bit vague.)

. . . thereby saving his tale for us to hear.

In our variation, we start with n people numbered 1 to n around a circle, and we eliminate every second remaining person until only one survives. For example, here’s the starting configuration for n = 10:

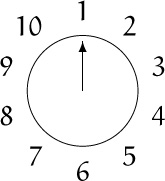
The elimination order is 2, 4, 6, 8, 10, 3, 7, 1, 9, so 5 survives. The problem: Determine the survivor’s number, J(n).

Here’s a case where n = 0 makes no sense.

We just saw that J(10) = 5. We might conjecture that J(n) = n/2 when n is even; and the case n = 2 supports the conjecture: J(2) = 1. But a few other small cases dissuade us—the conjecture fails for n = 4 and n = 6.

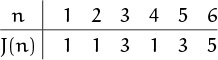
Even so, a bad guess isn’t a waste of time, because it gets us involved in the problem.

It’s back to the drawing board; let’s try to make a better guess. Hmmm . . . J(n) always seems to be odd. And in fact, there’s a good reason for this: The first trip around the circle eliminates all the even numbers. Furthermore, if n itself is an even number, we arrive at a situation similar to what we began with, except that there are only half as many people, and their numbers have changed.

So let’s suppose that we have 2n people originally. After the first go-round, we’re left with

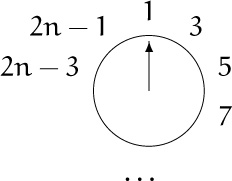
and 3 will be the next to go. This is just like starting out with n people, except that each person’s number has been doubled and decreased by 1. That is,

J(2n) = 2J(n) – 1,          for n ≥ 1.

This is the tricky part: We have J(2n) = newnumber (J(n)), where newnumber (k) = 2k – 1.

We can now go quickly to large n. For example, we know that J(10) = 5, so

J(20) = 2J(10) – 1 = 2·5 – 1 = 9.

Similarly J(40) = 17, and we can deduce that J(5·2^m) = 2^m+1 + 1.

But what about the odd case? With 2n + 1 people, it turns out that person number 1 is wiped out just after person number 2n, and we’re left with

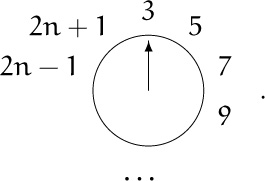
Again we almost have the original situation with n people, but this time their numbers are doubled and increased by 1. Thus

J(2n + 1) = 2J(n) + 1,          for n ≥ 1.

Odd case? Hey, leave my brother out of it.

Combining these equations with J(1) = 1 gives us a recurrence that defines J in all cases:

Instead of getting J(n) from J(n – 1), this recurrence is much more “efficient,” because it reduces n by a factor of 2 or more each time it’s applied. We could compute J(1000000), say, with only 19 applications of (1.8). But still, we seek a closed form, because that will be even quicker and more informative. After all, this is a matter of life or death.

Our recurrence makes it possible to build a table of small values very quickly. Perhaps we’ll be able to spot a pattern and guess the answer.

Voilà! It seems we can group by powers of 2 (marked by vertical lines in the table); J(n) is always 1 at the beginning of a group and it increases by 2 within a group. So if we write n in the form n = 2^m + l, where 2^m is the largest power of 2 not exceeding n and where l is what’s left, the solution to our recurrence seems to be

(Notice that if 2^m ≤ n < 2^m+1, the remainder l = n – 2^m satisfies 0 ≤ l < 2^m+1 – 2^m = 2^m.)

We must now prove (1.9). As in the past we use induction, but this time the induction is on m. When m = 0 we must have l = 0; thus the basis of (1.9) reduces to J(1) = 1, which is true. The induction step has two parts, depending on whether l is even or odd. If m > 0 and 2^m + l is equal to 2k, for some integer k, then l is even and

J(2^m + l) = 2J(2^m–1 + l/2) – 1 = 2(2l/2 + 1) – 1 = 2l + 1,

by (1.8) and the induction hypothesis; this is exactly what we want. A similar proof works in the odd case, when 2^m + l = 2k + 1. We might also note that (1.8) implies the relation

J(2n + 1) – J(2n) = 2.

Either way, the induction is complete and (1.9) is established.

But there’s a simpler way! The key fact is that J(2^m) = 1 for all m, and this follows immediately from our first equation, J(2n) = 2J(n)–1. Hence we know that the first person will survive whenever n is a power of 2. And in the general case, when n = 2^m + l, the number of people is reduced to a power of 2 after there have been l executions. The first remaining person at this point, the survivor, is number 2l + 1.

To illustrate solution (1.9), let’s compute J(100). In this case we have 100 = 2⁶ + 36, so J(100) = 2·36 + 1 = 73.

Now that we’ve done the hard stuff (solved the problem) we seek the soft: Every solution to a problem can be generalized so that it applies to a wider class of problems. Once we’ve learned a technique, it’s instructive to look at it closely and see how far we can go with it. Hence, for the rest of this section, we will examine the solution (1.9) and explore some generalizations of the recurrence (1.8). These explorations will uncover the structure that underlies all such problems.

Powers of 2 played an important role in our finding the solution, so it’s natural to look at the radix 2 representations of n and J(n). Suppose n’s binary expansion is

n = (b_m b_m–1 . . . b₁ b₀)₂;

that is,

n = b_m2^m + b_m–12^m–1 + · · · + b₁2 + b₀ ,

where each b_i is either 0 or 1 and where the leading bit b_m is 1. Recalling that n = 2^m + l, we have, successively,

n =	(1 bm–1 bm–2 . . . b1 b0)2 ,
l =	(0 bm–1 bm–2 . . . b1 b0)2 ,
2l =	(bm–1 bm–2 . . . b1 b0 0)2 ,
2l + 1 =	(bm–1 bm–2 . . . b1 b0 1)2 ,
J(n) =	(bm–1 bm–2 . . . b1 b0 bm)2 .

(The last step follows because J(n) = 2l + 1 and because b_m = 1.) We have proved that

that is, in the lingo of computer programming, we get J(n) from n by doing a one-bit cyclic shift left! Magic. For example, if n = 100 = (1100100)₂ then J(n) = J((1100100)₂)= (1001001)₂, which is 64 + 8 + 1 = 73. If we had been working all along in binary notation, we probably would have spotted this pattern immediately.

If we start with n and iterate the J function m + 1 times, we’re doing m + 1 one-bit cyclic shifts; so, since n is an (m+1)-bit number, we might expect to end up with n again. But this doesn’t quite work. For instance if n = 13 we have J((1101)₂) = (1011)₂, but then J((1011)₂) = (111)₂ and the process breaks down; the 0 disappears when it becomes the leading bit. In fact, J(n) must always be ≤ n by definition, since J(n) is the survivor’s number; hence if J(n) < n we can never get back up to n by continuing to iterate.

(“Iteration” here means applying a function to itself.)

Repeated application of J produces a sequence of decreasing values that eventually reach a “fixed point,” where J(n) = n. The cyclic shift property makes it easy to see what that fixed point will be: Iterating the function enough times will always produce a pattern of all 1’s whose value is 2^ν(n) – 1, where ν(n) is the number of 1 bits in the binary representation of n. Thus, since ν(13) = 3, we have

similarly

Curiously enough, if M is a compact C^∞ n-manifold (n > 1), there exists a differentiable immersion of M into R^2n–ν(n) but not necessarily into R^{2n–ν(n)–1}. I wonder if Josephus was secretly a topologist?

Curious, but true.

Let’s return briefly to our first guess, that J(n) = n/2 when n is even. This is obviously not true in general, but we can now determine exactly when it is true:

J(n) =	n/2,
2l + 1 =	(2m + l)/2,
l =	(2m – 2) .

If this number is an integer, then n = 2^m + l will be a solution, because l will be less than 2^m. It’s not hard to verify that 2^m – 2 is a multiple of 3 when m is odd, but not when m is even. (We will study such things in Chapter 4.) Therefore there are infinitely many solutions to the equation J(n) = n/2, beginning as follows:

Notice the pattern in the rightmost column. These are the binary numbers for which cyclic-shifting one place left produces the same result as ordinary-shifting one place right (halving).

OK, we understand the J function pretty well; the next step is to generalize it. What would have happened if our problem had produced a recurrence that was something like (1.8), but with different constants? Then we might not have been lucky enough to guess the solution, because the solution might have been really weird. Let’s investigate this by introducing constants α, β, and γ and trying to find a closed form for the more general recurrence

Looks like Greek to me.

(Our original recurrence had α = 1, β = –1, and γ = 1.) Starting with f(1) = α and working our way up, we can construct the following general table for small values of n:

It seems that α’s coefficient is n’s largest power of 2. Furthermore, between powers of 2, β’s coefficient decreases by 1 down to 0 and γ’s increases by 1 up from 0. Therefore if we express f(n) in the form

by separating out its dependence on α, β, and γ, it seems that

Here, as usual, n = 2^m + l and 0 ≤ l < 2^m, for n ≥ 1.

It’s not terribly hard to prove (1.13) and (1.14) by induction, but the calculations are messy and uninformative. Fortunately there’s a better way to proceed, by choosing particular values and then combining them. Let’s illustrate this by considering the special case α = 1, β = γ = 0, when f(n) is supposed to be equal to A(n): Recurrence (1.11) becomes

A(1) =	1;
A(2n) =	2A(n),	for n ≥ 1;
A(2n + 1) =	2A(n) ,	for n ≥ 1.

Hold onto your hats, this next part is new stuff.

Sure enough, it’s true (by induction on m) that A(2^m + l) = 2^m.

Next, let’s use recurrence (1.11) and solution (1.13) in reverse, by starting with a simple function f(n) and seeing if there are any constants (α, β, γ) that will define it. Plugging the constant function f(n) = 1 into (1.11) says that

1 = α;

1 = 2·1 + β;

1 = 2·1 + γ;

hence the values (α, β, γ) = (1, –1, –1) satisfying these equations will yield A(n) – B(n) – C(n) = f(n) = 1. Similarly, we can plug in f(n) = n:

1 =	α;
2n =	2·n + β;
2n + 1 =	2·n + γ.

A neat idea!

These equations hold for all n when α = 1, β = 0, and γ = 1, so we don’t need to prove by induction that these parameters will yield f(n) = n. We already know that f(n) = n will be the solution in such a case, because the recurrence (1.11) uniquely defines f(n) for every value of n.

And now we’re essentially done! We have shown that the functions A(n), B(n), and C(n) of (1.13), which solve (1.11) in general, satisfy the equations

A(n) =	2m,	where n = 2m + l and 0 ≤ l < 2m;
A(n) – B(n) – C(n) =	1;
A(n) + C(n) =	n.

Our conjectures in (1.14) follow immediately, since we can solve these equations to get C(n) = n – A(n) = l and B(n) = A(n) – 1 – C(n) = 2^m – 1 – l.

Beware: The authors are expecting us to figure out the idea of the repertoire method from seat-of-the-pants examples, instead of giving us a top-down presentation. The method works best with recurrences that are “linear,” in the sense that the solutions can be expressed as a sum of arbitrary parameters multiplied by functions of n, as in (1.13). Equation (1.13) is the key.

This approach illustrates a surprisingly useful repertoire method for solving recurrences. First we find settings of general parameters for which we know the solution; this gives us a repertoire of special cases that we can solve. Then we obtain the general case by combining the special cases. We need as many independent special solutions as there are independent parameters (in this case three, for α, β, and γ). Exercises 16 and 20 provide further examples of the repertoire approach.

We know that the original J-recurrence has a magical solution, in binary:

J((b_m b_m–1 . . . b₁ b₀)₂) = (b_m–1 . . . b₁ b₀ b_m)₂,          where b_m = 1.

Does the generalized Josephus recurrence admit of such magic?

Sure, why not? We can rewrite the generalized recurrence (1.11) as

if we let β₀ = β and β₁ = γ. And this recurrence unfolds, binary-wise:

f (bm bm–1 . . . b1 b0)2	= 2f((bm bm–1 . . . b1)2) + βb0
	= 4f (bm bm–1 . . . b2)2 + 2βb1 + βb0
	⋮
	= 2mf((bm)2) +2m –1βbm–1+ · · · +2βb1+βb0
	= 2mα + 2m –1βbm–1 + · · · + 2βb1 + βb0 .

(‘relax’ = ‘destroy’)

Suppose we now relax the radix 2 notation to allow arbitrary digits instead of just 0 and 1. The derivation above tells us that

Nice. We would have seen this pattern earlier if we had written (1.12) in another way:

I think I get it: The binary representations of A(n), B(n), and C(n) have 1’s in different positions.

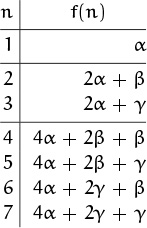
For example, when n = 100 = (1100100)₂, our original Josephus values α = 1, β = –1, and γ = 1 yield

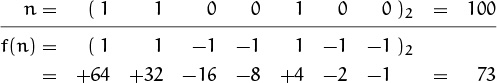
as before. The cyclic-shift property follows because each block of binary digits (1 0 . . . 0 0)₂ in the representation of n is transformed into

(1 –1 . . . –1 –1)₂ = (0 0 . . . 0 1)₂.

So our change of notation has given us the compact solution (1.16) to the general recurrence (1.15). If we’re really uninhibited we can now generalize even more. The recurrence

is the same as the previous one except that we start with numbers in radix d and produce values in radix c. That is, it has the radix-changing solution

“There are two kinds of generalizations. One is cheap and the other is valuable. It is easy to generalize by diluting a little idea with a big terminology. It is much more difficult to prepare a refined and condensed extract from several good ingredients.”

—G. Pólya [297]

For example, suppose that by some stroke of luck we’re given the recurrence

f(1) =	34;
f(2) =	5;
f(3n) =	10f(n) + 76,	for n ≥ 1;
f(3n + 1) =	10f(n) – 2,	for n ≥ 1;
f(3n + 2) =	10f(n) + 8,	for n ≥ 1;

and suppose we want to compute f(19). Here we have d = 3 and c = 10. Now 19 = (201)₃, and the radix-changing solution tells us to perform a digit-by-digit replacement from radix 3 to radix 10. So the leading 2 becomes a 5, and the 0 and 1 become 76 and –2, giving

f(19) = f((201)₃) = (5 76 –2)₁₀ = 1258,

which is our answer.

Perhaps this was a stroke of bad luck.

Thus Josephus and the Jewish–Roman war have led us to some interesting general recurrences.

But in general I’m against recurrences of war.

Exercises

Warmups

1. All horses are the same color; we can prove this by induction on the number of horses in a given set. Here’s how: “If there’s just one horse then it’s the same color as itself, so the basis is trivial. For the induction step, assume that there are n horses numbered 1 to n. By the induction hypothesis, horses 1 through n – 1 are the same color, and similarly horses 2 through n are the same color. But the middle horses, 2 through n – 1, can’t change color when they’re in different groups; these are horses, not chameleons. So horses 1 and n must be the same color as well, by transitivity. Thus all n horses are the same color; QED.” What, if anything, is wrong with this reasoning?

Please do all the warmups in all the chapters!

—The Mgm’t

2. Find the shortest sequence of moves that transfers a tower of n disks from the left peg A to the right peg B, if direct moves between A and B are disallowed. (Each move must be to or from the middle peg. As usual, a larger disk must never appear above a smaller one.)

3. Show that, in the process of transferring a tower under the restrictions of the preceding exercise, we will actually encounter every properly stacked arrangement of n disks on three pegs.

4. Are there any starting and ending configurations of n disks on three pegs that are more than 2ⁿ – 1 moves apart, under Lucas’s original rules?

5. A “Venn diagram” with three overlapping circles is often used to illustrate the eight possible subsets associated with three given sets:

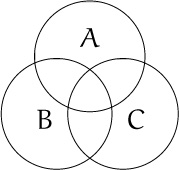
Can the sixteen possibilities that arise with four given sets be illustrated by four overlapping circles?

6. Some of the regions defined by n lines in the plane are infinite, while others are bounded. What’s the maximum possible number of bounded regions?

7. Let H(n) = J(n + 1) – J(n). Equation (1.8) tells us that H(2n) = 2, and H(2n+1) = J(2n+2)–J(2n+1) = (2J(n+1)–1) – (2J(n)+1) = 2H(n)–2, for all n ≥ 1. Therefore it seems possible to prove that H(n) = 2 for all n, by induction on n. What’s wrong here?

Homework exercises

8. Solve the recurrence

Q₀ = α;          Q₁ = β;

Q_n = (1 + Q_n–1)/Q_n–2,          for n > 1.

Assume that Q_n ≠ 0 for all n ≥ 0. Hint: Q₄ = (1 + α)/β.

9. Sometimes it’s possible to use induction backwards, proving things from n to n – 1 instead of vice versa! For example, consider the statement

. . . now that’s a horse of a different color.

This is true when n = 2, since (x₁ + x₂)² – 4x₁x₂ = (x₁ – x₂)² ≥ 0.

a. By setting x_n = (x₁ + · · · + x_n–1)/(n – 1), prove that P(n) implies P(n – 1) whenever n > 1.

b. Show that P(n) and P(2) imply P(2n).

c. Explain why this implies the truth of P(n) for all n.

10. Let Q_n be the minimum number of moves needed to transfer a tower of n disks from A to B if all moves must be clockwise—that is, from A to B, or from B to the other peg, or from the other peg to A. Also let R_n be the minimum number of moves needed to go from B back to A under this restriction. Prove that

(You need not solve these recurrences; we’ll see how to do that in Chapter 7.)

11. A Double Tower of Hanoi contains 2n disks of n different sizes, two of each size. As usual, we’re required to move only one disk at a time, without putting a larger one over a smaller one.

a. How many moves does it take to transfer a double tower from one peg to another, if disks of equal size are indistinguishable from each other?

b. What if we are required to reproduce the original top-to-bottom order of all the equal-size disks in the final arrangement? [Hint: This is difficult—it’s really a “bonus problem.”]

12. Let’s generalize exercise 11a even further, by assuming that there are n different sizes of disks and exactly m_k disks of size k. Determine A(m₁, . . . , m_n), the minimum number of moves needed to transfer a tower when equal-size disks are considered to be indistinguishable.

13. What’s the maximum number of regions definable by n zig-zag lines,

each of which consists of two parallel infinite half-lines joined by a straight segment?

14. How many pieces of cheese can you obtain from a single thick piece by making five straight slices? (The cheese must stay in its original position while you do all the cutting, and each slice must correspond to a plane in 3D.) Find a recurrence relation for P_n, the maximum number of three-dimensional regions that can be defined by n different planes.

Good luck keeping the cheese in position.

15. Josephus had a friend who was saved by getting into the next-to-last position. What is I(n), the number of the penultimate survivor when every second person is executed?

16. Use the repertoire method to solve the general four-parameter recurrence

g(1) =	α;
g(2n + j) =	3g(n) + γn + βj,	for j = 0, 1     and     n ≥ 1.

Hint: Try the function g(n) = n.

Exam problems

17. If W_n is the minimum number of moves needed to transfer a tower of n disks from one peg to another when there are four pegs instead of three, show that

W_n(n+1)/2 ≤ 2W_n(n–1)/2 + T_n,          for n > 0.

(Here T_n = 2ⁿ – 1 is the ordinary three-peg number.) Use this to find a closed form f(n) such that W_n(n+1)/2 ≤ f(n) for all n ≥ 0.

18. Show that the following set of n bent lines defines Z_n regions, where Z_n is defined in (1.7): The jth bent line, for 1 ≤ j ≤ n, has its zig at (n^2j, 0) and goes up through the points (n^2j – n^j, 1) and (n^2j – n^j – n^–n, 1).

19. Is it possible to obtain Z_n regions with n bent lines when the angle at each zig is 30°?

20. Use the repertoire method to solve the general five-parameter recurrence

h(1) =	α;
h(2n + j) =	4h(n) + γjn + βj,	for j = 0, 1     and     n ≥ 1.

Hint: Try the functions h(n) = n and h(n) = n².

Is this like a five-star general recurrence?

21. Suppose there are 2n people in a circle; the first n are “good guys” and the last n are “bad guys.” Show that there is always an integer q (depending on n) such that, if we go around the circle executing every qth person, all the bad guys are first to go. (For example, when n = 3 we can take q = 5; when n = 4 we can take q = 30.)

Bonus problems

22. Show that it’s possible to construct a Venn diagram for all 2ⁿ possible subsets of n given sets, using n convex polygons that are congruent to each other and rotated about a common center.

23. Suppose that Josephus finds himself in a given position j, but he has a chance to name the elimination parameter q such that every qth person is executed. Can he always save himself?

Research problems

24. Find all recurrence relations of the form

whose solution is periodic regardless of the initial values X₀, . . . , X_k–1.

25. Solve infinitely many cases of the four-peg Tower of Hanoi problem by proving that equality holds in the relation of exercise 17.

26. Generalizing exercise 23, let’s say that a Josephus subset of {1, 2, . . . , n} is a set of k numbers such that, for some q, the people with the other n–k numbers will be eliminated first. (These are the k positions of the “good guys” Josephus wants to save.) It turns out that when n = 9, three of the 2⁹ possible subsets are non-Josephus, namely {1, 2, 5, 8, 9}, {2, 3, 4, 5, 8}, and {2, 5, 6, 7, 8}. There are 13 non-Josephus sets when n = 12, none for any other values of n ≤ 12. Are non-Josephus subsets rare for large n?

Yes, and well done if you find them.