A. Answers to Exercises

Every exercise is answered here (at least briefly), and some of these answers go beyond what was asked. Readers will learn best if they make a serious attempt to find their own answers BEFORE PEEKING at this appendix.

The authors will be interested to learn of any solutions (or partial solutions) to the research problems, or of any simpler (or more correct) ways to solve the non-research ones.

(The first finder of every error in this book will receive a reward of $2.56.)

1.1 The proof is fine except when n = 2. If all sets of two horses have horses of the same color, the statement is true for any number of horses.

Does that mean I have to find every error?

1.2 If X_n is the number of moves, we have X₀ = 0 and X_n = X_n–1 + 1 + X_n–1 + 1 + X_n–1 when n > 0. It follows (for example by adding 1 to both sides) that X_n = 3ⁿ –1. (After moves, it turns out that the entire tower will be on the middle peg, halfway home!)

(We meant to say “any error.”)

Does that mean only one person gets a reward?

1.3 There are 3ⁿ possible arrangements, since each disk can be on any of the pegs. We must hit them all, since the shortest solution takes 3ⁿ –1 moves. (This construction is equivalent to a “ternary Gray code,” which runs through all numbers from (0 . . . 0)₃ to (2 . . . 2)₃, changing only one digit at a time.)

(Hmmm. Try it and see.)

1.4 No. If the largest disk doesn’t have to move, 2^n–1 –1 moves will suffice (by induction); otherwise (2^n–1 – 1) + 1 + (2^n–1 – 1) will suffice (again by induction).

1.5 No; different circles can intersect in at most two points, so the fourth circle can increase the number of regions to at most 14. However, it is possible to do the job with ovals:

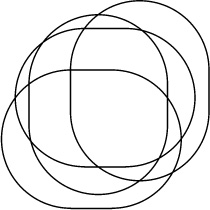
The number of intersection points turns out to give the whole story; convexity was a red herring.

Venn [359] claimed that there is no way to do the five-set case with ellipses, but a five-set construction with ellipses was found by Grünbaum [167].

1.6 If the nth line intersects the previous lines in k > 0 distinct points, we get k – 1 new bounded regions (assuming that none of the previous lines were mutually parallel) and two new infinite regions. Hence the maximum number of bounded regions is (n–2)+(n–3)+· · · = S_n–2 = (n–1)(n–2)/2 = L_n–2n.

This answer assumes that n > 0.

1.7 The basis is unproved; and in fact, H(1) ≠ 2.

1.8 Q₂ = (1 + β)/α; Q₃ = (1 + α + β)/αβ; Q₄ = (1 + α)/β; Q₅ = α; Q₆ = β. So the sequence is periodic!

1.9 (a) We get P(n – 1) from the inequality

(b) x₁ . . . x_nx_n+1 . . . x_2n ≤ (((x₁ + · · · + x_n)/n)((x_n+1 + · · · + x_2n)/n))ⁿ by P(n); the product inside is ≤ ((x₁ + · · · +x_2n)/2n)² by P(2). (c) For example, P(5) follows from P(6) from P(3) from P(4) from P(2).

1.10 First show that R_n = R_n–1 + 1 + Q_n–1 + 1 + R_n–1, when n > 0. Incidentally, the methods of Chapter 7 will tell us that Q_n = ((1 + )ⁿ⁺¹ – (1 – )ⁿ⁺¹)/(2) – 1.

1.11 (a) We cannot do better than to move a double (n – 1)-tower, then move (and invert the order of) the two largest disks, then move the double (n – 1)-tower again; hence A_n = 2A_n–1 + 2 and A_n = 2T_n = 2ⁿ⁺¹ – 2. This solution interchanges the two largest disks but returns the other 2n – 2 to their original order.

(b) Let B_n be the minimum number of moves. Then B₁ = 3, and it can be shown that no strategy does better than B_n = A_n–1 +2+A_n–1 +2+B_n–1 when n > 1. Hence B_n = 2ⁿ⁺²–5, for all n > 0. Curiously this is just 2A_n–1, and we also have B_n = A_n–1 + 1 + A_n–1 + 1 + A_n–1 + 1 + A_n–1.

1.12 If all m_k > 0, then A(m₁, . . . , m_n) = 2A(m₁, . . . , m_n–1)+m_n. This is an equation of the “generalized Josephus” type, with solution (m₁ . . . m_n)₂ = 2^n–1m₁ + · · · + 2m_n–1 + m_n.

Incidentally, the corresponding generalization of exercise 11b appears to satisfy the recurrence

1.13 Given n straight lines that define L_n regions, we can replace them by extremely narrow zig-zags with segments sufficiently long that there are nine intersections between each pair of zig-zags. This shows that ZZ_n = ZZ_n–1+9n–8, for all n > 0; consequently ZZ_n = 9S_n – 8n + 1 = n² – n + 1.

1.14 The number of new 3-dimensional regions defined by each new cut is the number of 2-dimensional regions defined in the new plane by its intersections with the previous planes. Hence P_n = P_n–1 + L_n–1, and it turns out that P₅ = 26. (Six cuts in a cubical piece of cheese can make 27 cubelets, or up to P₆ = 42 cuts of weirder shapes.)

Incidentally, the solution to this recurrence fits into a nice pattern if we express it in terms of binomial coefficients (see Chapter 5):

I bet I know what happens in four dimensions!

Here X_n is the maximum number of 1-dimensional regions definable by n points on a line.

1.15 The function I satisfies the same recurrence as J when n > 1, but I(1) is undefined. Since I(2) = 2 and I(3) = 1, there’s no value of I(1) = α that will allow us to use our general method; the “end game” of unfolding depends on the two leading bits in n’s binary representation.

If n = 2^m + 2^m–1 + k, where 0 ≤ k < 2^m+1 + 2^m – (2^m + 2^m–1) = 2^m +2^m–1, the solution is I(n) = 2k+1 for all n > 2. Another way to express this, in terms of the representation n = 2^m + l, is to say that

1.16 Let g(n) = a(n)α + b(n)β₀ + c(n)β₁ + d(n)γ. We know from (1.18) that a(n)α + b(n)β₀ + c(n)β₁ = (α β_bm–1 β_bm–2 . . . β_b1 β_b0)₃ when n = (1 b_m–1 . . . b₁ b₀)₂; this defines a(n), b(n), and c(n). Setting g(n) = n in the recurrence implies that a(n) + c(n) – d(n) = n; hence we know everything. [Setting g(n) = 1 gives the additional identity a(n) – 2b(n) – 2c(n) = 1, which can be used to define b(n) in terms of the simpler functions a(n) and a(n) + c(n).]

1.17 In general we have W_m ≤ 2W_m–k + T_k, for 0 ≤ k ≤ m. (This relation corresponds to transferring the top m – k, then using only three pegs to move the bottom k, then finishing with the top m – k.) The stated relation turns out to be based on the unique value of k that minimizes the right-hand side of this general inequality, when m = n(n + 1)/2. (However, we cannot conclude that equality holds; many other strategies for transferring the tower are conceivable.) If we set Y_n = (W_n(n+1)/2 – 1)/2ⁿ, we find that Y_n ≤ Y_n–1 + 1; hence W_n(n+1)/2 ≤ 2ⁿ(n – 1) + 1.

1.18 It suffices to show that both of the lines from (n^2j, 0) intersect both of the lines from (n^2k, 0), and that all these intersection points are distinct.

A line from (x_j, 0) through (x_j – a_j, 1) intersects a line from (x_k, 0) through (x_k – a_k, 1) at the point (x_j – ta_j, t) where t = (x_k – x_j)/(a_k – a_j). Let x_j = n^2j and a_j = n^j + (0 or n^–n). Then the ratio t = (n^2k – n^2j)/(n^k – n^j + (–n^–n or 0 or n^–n)) lies strictly between n^j + n^k – 1 and n^j + n^k + 1; hence the y coordinate of the intersection point uniquely identifies j and k. Also the four intersections that have the same j and k are distinct.

1.19 Not when n > 5. A bent line whose half-lines run at angles θ and θ + 30^° from its apex can intersect four times with another whose half-lines run at angles ϕ and ϕ + 30^° only if 30^° < |θ – ϕ| < 150^°. We can’t choose more than 5 angles this far apart from each other. (It is possible to choose 5.)

1.20 Let h(n) = a(n)α + b(n)β₀ + c(n)β₁ + d(n)γ₀ + e(n)γ₁. We know from (1.18) that a(n)α + b(n)β₀ + c(n)β₁ = (α β_bm–1 β_bm–2 . . . β_b1 β_b0)₄ when n = (1 b_m–1 . . . b₁ b₀)₂; this defines a(n), b(n), and c(n). Setting h(n) = n in the recurrence implies that a(n) + c(n) – 2d(n) – 2e(n) = n; setting h(n) = n² implies that a(n) + c(n) + 4e(n) = n². Hence d(n) = (3a(n) + 3c(n) – n² – 2n)/4; e(n) = (n² – a(n) – c(n)) /4.

1.21 We can let q be the least (or any) common multiple of 2n, 2n – 1, . . . , n + 1. [A non-rigorous argument suggests that a “random” value of q will succeed with probability

so we might expect to find such a q less than 4ⁿ.]

1.22 Take a regular polygon with 2ⁿ sides and label the sides with the elements of a “de Bruijn cycle” of length 2ⁿ. (This is a cyclic sequence of 0’s and 1’s in which all n-tuples of adjacent elements are different; see [207, exercise 2.3.4.2–23] and [208, exercise 3.2.2–17].) Attach a very thin convex extension to each side that’s labeled 1. The n sets are copies of the resulting polygon, rotated by the length of k sides for k = 0, 1, . . . , n – 1.

I once rode a de Bruijn cycle (when visiting at his home in Nuenen, The Netherlands).

1.23 Yes. (We need principles of elementary number theory from Chapter 4.) Let L(n) = lcm(1, 2, . . . , n). We can assume that n > 2; hence by Bertrand’s postulate there is a prime p between n/2 and n. We can also assume that j > n/2, since q′ = L(n) + 1 – q leaves j′ = n + 1 – j if and only if q leaves j. Choose q so that q ≡ 1 (mod L(n)/p) and q ≡ j + 1 – n (mod p). The people are now removed in order 1, 2, . . . , n – p, j + 1, j + 2, . . . , n, n – p + 1, . . . , j – 1.

1.24 The only known examples are: X_n = 2i sin πr + 1/X_n–1, where r is rational and 0 ≤ r < (all period lengths ≥ 2 occur as r varies); Gauss’s recurrence of period 5 in exercise 8; H. Todd’s even more remarkable recurrence X_n = (1+X_n–1+X_n–2)/X_n–3, which has period 8 (see [261]); and recurrences derived from these when we replace X_n by a constant times X_mn. We can assume that the first nonzero coefficient in the denominator is unity, and that the first nonzero coefficient in the numerator (if any) has nonnegative real part. Computer algebra shows easily that there are no further solutions of period ≤ 5 when k = 2. A partial theory has been developed by Lyness [261, 262] and by Kurshan and Gopinath [231].

An interesting example of another type, with period 9 when the starting values are real, is the recurrence X_n = |X_n–1|–X_n–2 discovered by Morton Brown [43]. Nonlinear recurrences having any desired period ≥ 5 can be based on continuants [65].

1.25 If T^(k)(n) denotes the minimum number of moves needed to transfer n disks with k auxiliary pegs (hence T⁽¹⁾(n) = T_n and T⁽²⁾(n) = W_n), we have . No examples (n, k) are known where this inequality fails to be an equality. When k is small compared with n, the formula 2^n+1–k gives a convenient upper bound on .

1.26 The execution-order permutation can be computed in O(n log n) steps for all q and n [209, exercises 5.1.1–2 and 5.1.1–5]. Bjorn Poonen has proved that non-Josephus sets with exactly four “bad guys” exist whenever n ≡ 0 (mod 3) and n ≥ 9; in fact, the number of such sets is at least for some > 0. He also found by extensive computations that the only other n < 24 with non-Josephus sets is n = 20, which has 236 such sets with k = 14 and two with k = 13. (One of the latter is {1, 2, 3, 4, 5, 6, 7, 8, 11, 14, 15, 16, 17}; the other is its reflection with respect to 21.) There is a unique non-Josephus set with n = 15 and k = 9, namely {3, 4, 5, 6, 8, 10, 11, 12, 13}.

2.1 There’s no agreement about this; three answers are defensible: (1) We can say that is always equivalent to ∑_m≤k≤n q_k; then the stated sum is zero. (2) A person might say that the given sum is q₄ + q₃ + q₂ + q₁ + q₀, by summing over decreasing values of k. But this conflicts with the generally accepted convention that when n = 0. (3) We can say that ; then the stated sum is equal to – q₁ – q₂ – q₃. This convention may appear strange, but it obeys the useful law for all a, b, c.

It’s best to use the notation only when n – m ≥ –1; then both conventions (1) and (3) agree.

2.2 This is |x|. Incidentally, the quantity ([x > 0] – [x < 0]) is often called sign(x) or signum(x); it is +1 when x > 0, 0 when x = 0, and –1 when x < 0.

2.3 The first sum is, of course, a₀ + a₁ + a₂ + a₃ + a₄ + a₅; the second is a₄ + a₁ + a₀ + a₁ + a₄, because the sum is over the values k ∈ {–2, –1, 0, +1, +2}. The commutative law doesn’t apply here because the function p(k) = k² is not a permutation. Some values of n (e.g., n = 3) have no k such that p(k) = n; others (e.g., n = 4) have two such k.

2.4 (a)

(b)

2.5 The same index ‘k’ is being used for two different index variables, although k is bound in the inner sum. This is a famous mistake in mathematics (and computer programming). The result turns out to be correct if a_j = a_k for all j and k, 1 ≤ j, k ≤ n.

2.6 It’s [1 ≤ j ≤ n](n – j + 1). The first factor is necessary here because we should get zero when j < 1 or j > n.

2.7 . A version of finite calculus based on ∇ instead of Δ would therefore give special prominence to rising factorial powers.

2.8 0, if m ≥ 1; 1/|m|!, if m ≤ 0.

2.9 , for integers m and n. Setting m = –n tells us that .

2.10 Another possible right-hand side is Eu Δv + v Δu.

2.11 Break the left-hand side into two sums, and change k to k + 1 in the second of these.

2.12 If p(k) = n then n + c = k + ((–1)^k + 1)c and ((–1)^k + 1) is even; hence (–1)^n+c = (–1)^k and k = n – (–1)^n+cc. Conversely, this value of k yields p(k) = n.

2.13 Let R₀ = α, and R_n = R_n–1 + (–1)ⁿ(β + nγ + n²δ) for n > 0. Then R(n) = A(n)α + B(n)β + C(n)γ + D(n)δ. Setting R_n = 1 yields A(n) = 1. Setting R_n = (–1)ⁿ yields A(n) + 2B(n) = (–1)ⁿ. Setting R_n = (–1)ⁿn yields –B(n)+2C(n) = (–1)ⁿn. Setting R_n = (–1)ⁿn² yields B(n)–2C(n) + 2D(n) = (–1)ⁿn². Therefore 2D(n) = (–1)ⁿ(n²+n); the stated sum is D(n).

2.14 The suggested rewrite is legitimate since we have k = ∑_1≤j≤k 1 when 1 ≤ k ≤ n. Sum first on k; the multiple sum reduces to

2.15 The first step replaces k(k + 1) by 2∑_1≤j≤k j. The second step gives .

2.16 , by (2.52).

2.17 Use induction for the first two =’s, and (2.52) for the third. The second line follows from the first.

2.18 Use the facts that (ℜz)⁺ ≤ |z|, (ℜz)^– ≤ |z|, (ℑz)⁺ ≤ |z|, (ℑz)^– ≤ |z|, and |z| ≤ (ℜz)⁺ + (ℜz)^– + (ℑz)⁺ + (ℑz)^–.

2.19 Multiply both sides by 2^n–1/n! and let S_n = 2ⁿT_n/n! = S_n–1 + 3 · 2^n–1 = 3(2ⁿ – 1) + S₀. The solution is T_n = 3 · n! + n!/2^n–1. (We’ll see in Chapter 4 that T_n is an integer only when n is 0 or a power of 2.)

“It is a profoundly erroneous truism, repeated by all copybooks and by eminent people when they are making speeches, that we should cultivate the habit of thinking of what we are doing. The precise opposite is the case. Civilization advances by extending the number of important operations which we can perform without thinking about them. Operations of thought are like cavalry charges in a battle—they are strictly limited in number, they require fresh horses, and must only be made at decisive moments.”

—A. N. Whitehead [370]

2.20 The perturbation method gives

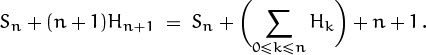
2.21 Extracting the final term of S_n+1 gives S_n+1 = 1 – S_n; extracting the first term gives

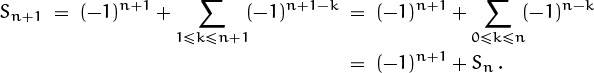
Hence 2S_n = 1 + (–1)ⁿ and we have S_n = [n is even]. Similarly, we find

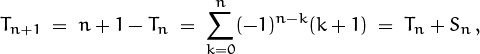
hence 2T_n = n + 1 – S_n and we have T_{n =} (n + [n is odd]). Finally, the same approach yields

Un+1 = (n + 1)2 – Un	=	Un + 2Tn + Sn
	=	Un + n + [n is odd] + [n is even]
	=	Un + n + 1.

Hence U_n is the triangular number .

2.22 Twice the general sum gives a “vanilla” sum over 1 ≤ j, k ≤ n, which splits and yields twice (∑_k a_kA_k)(∑_k b_kB_k) – (∑_k a_kB_k) (∑_k b_kA_k).

2.23 (a) This approach gives four sums that evaluate to 2n + H_n – 2n + (H_n + – 1). (It would have been easier to replace the summand by 1/k + 1/(k + 1).) (b) Let u(x) = 2x + 1 and Δv(x) = 1/x(x + 1) = (x – 1)^–2; then Δu(x) = 2 and v(x) = –(x – 1)^–1 = –1/x. The answer is .

2.24 Summing by parts, Σx^mH_x δx = x^{m + 1}H_x/(m+1)–x^m+1/(m+1)² +C; hence Σ_0≤k<n k^mH_k = n^{m + 1} (H_n – 1/(m + 1))/(m + 1) + 0^{m + 1}/(m + 1)². In our case m = –2, so the sum comes to 1 – (H_n + 1)/(n + 1).

2.25 Here are some of the basic analogies:

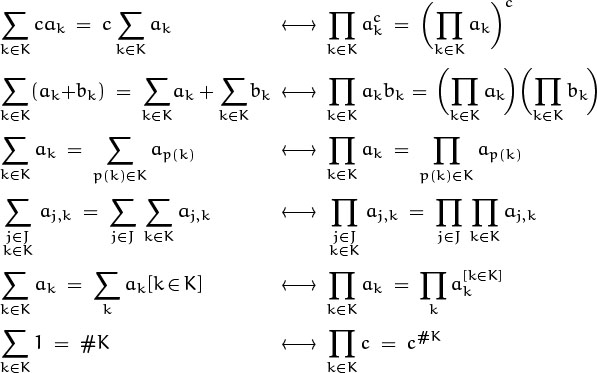
2.26 P² = (∏_1≤j,k≤n a_ja_k)(∏_1≤j=k≤n a_ja_k). The first factor is equal to ; the second factor is . Hence .

2.27 Δ(c^x) = c^x(c – x – 1) = c^x+2/(c – x). Setting c = –2 and decreasing x by 2 yields Δ(–(–2)^x–2) = (–2)^x/x, hence the stated sum is (–2)^–1 – (–2)^{n – 1} = (–1)ⁿn! – 1.

2.28 The interchange of summation between the second and third lines is not justifiable; the terms of this sum do not converge absolutely. Everything else is perfectly correct, except that the result of ∑_k≥1[k = j – 1]k/j should perhaps have been written [j – 1 ≥ 1](j – 1)/j and simplified explicitly.

As opposed to imperfectly correct.

2.29 Use partial fractions to get

The (–1)^k factor now makes the two halves of each term cancel with their neighbors. Hence the answer is –1/4 + (–1)ⁿ/(8n + 4).

2.30 . So we have

(b – a)(b + a – 1) = 2100 = 2² ·3·5² ·7.

There is one solution for each way to write 2100 = x · y where x is even and y is odd; we let and . So the number of solutions is the number of divisors of 3 · 5² · 7, namely 12. In general, there are ∏_p>2(n_p + 1) ways to represent ∏_p p^n_p, where the products range over primes.

2.31 ∑_j,k≥2 j^–k = ∑_j≥2 1/j²(1 – 1/j) = ∑_j≥2 1/j(j – 1). The second sum is, similarly, 3/4.

2.32 If 2n ≤ x < 2n+1, the sums are 0+· · ·+n+(x–n–1)+· · ·+(x–2n) = n(x–n) = (x–1) + (x–3) + · · · + (x–2n+1). If 2n – 1 ≤ x < 2n they are, similarly, both equal to n(x – n). (Looking ahead to Chapter 3, the formula (x + 1)(x – (x + 1) covers both cases.)

2.33 If K is empty, ∧_k∈K a_k = ∞. The basic analogies are:

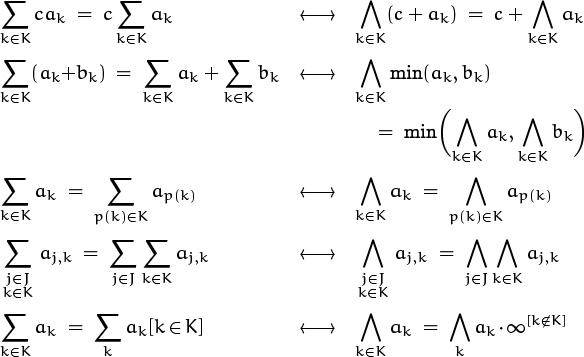
A permutation that consumes terms of one sign faster than those of the other can steer the sum toward any value that it likes.

2.34 Let K⁺ = {k | a_k ≥ 0} and K^– = {k | a_k < 0}. Then if, for example, n is odd, we choose F_n to be F_n–1 ∪ E_n, where E_n ⊆ K^– is sufficiently large that ∑_{k∈(Fn–1∩K⁺)} a_k – ∑_k∈En (–a_k) < A^–.

2.35 Goldbach’s sum can be shown to equal

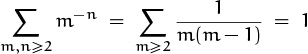
as follows: By unsumming a geometric series, it equals ∑_{k∈P, l≥1} k^–l; therefore the proof will be complete if we can find a one-to-one correspondence between ordered pairs (m, n) with m, n ≥ 2 and ordered pairs (k, l) with k ∈ P and l ≥ 1, where mⁿ = k^l when the pairs correspond. If m ∉ P we let (m, n) ↔ (mⁿ, 1); but if m = a^b ∈ P, we let (m, n) ↔ (aⁿ, b).

With this self-description, Golomb’s sequence wouldn’t do too well on the Dating Game.

2.36 (a) By definition, g(n) – g(n – 1) = f(n). (b) By part (a), g(g(n)) – g(g(n – 1)) = ∑_k f(k)[g(n – 1) < k ≤ g(n)] = n(g(n) – g(n – 1)) = nf(n). (c) By part (a) again, g(g(g(n))) – g(g(g(n – 1))) is

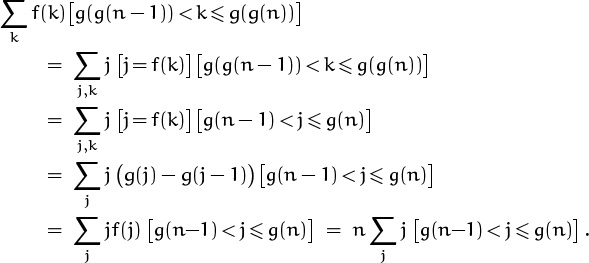
Colin Mallows observes that the sequence can also be defined by the recurrence

f(1) = 1;     f(n + 1) = 1 + f (n + 1 – f(f(n))),   for n ≥ 0.

2.37 (RLG thinks they probably won’t fit; DEK thinks they probably will; OP is not committing himself.)

3.1 m = lg n; l = n – 2^m = n – 2^{lg n}.

3.2 (a) x + .5. (b) x – .5.

3.3 This is mn – {mα}n/α = mn – 1, since 0 < {mα} < 1.

3.4 Something where no proof is required, only a lucky guess (I guess).

3.5 We have nx = nx + n{x} = nx + n{x} by (3.8) and (3.6). Therefore nx = nx ⇔ n{x} = 0 ⇔ 0 ≤ n{x} < 1 ⇔ {x} < 1/n, assuming that n is a positive integer. (Notice that nx ≤ nx for all x in this case.)

3.6 f(x) = f(x).

3.7 n/m + n mod m.

3.8 If all boxes contain < n/m objects, then n ≤ (n/m – 1) m, so n/m + 1 ≤ n/m, contradicting (3.5). The other proof is similar.

3.9 We have m/n–1/q = (n mumble m)/qn. The process must terminate, because 0 ≤ n mumble m < m. The denominators of the representation are strictly increasing, hence distinct, because qn/(n mumble m) > q.

3.10 x + – [(2x + 1)/4 is not an integer] is the nearest integer to x, if {x} ≠ ; otherwise it’s the nearest even integer. (See exercise 2.) Thus the formula gives an “unbiased” way to round.

3.11 If n is an integer, α < n < β ⇔ α < n < β. The number of integers satisfying a < n < b when a and b are integers is (b – a – 1)[b > a]. We would therefore get the wrong answer if α = β = integer.

3.12 Subtract n/m from both sides, by (3.6), getting (n mod m)/m = (n mod m + m – 1)/m. Both sides are now equal to [n mod m > 0], since 0 ≤ n mod m < m.

A shorter but less direct proof simply observes that the first term in (3.24) must equal the last term in (3.25).

3.13 If they form a partition, the text’s formula for N(α, n) implies that 1/α + 1/β = 1, because the coefficients of n in the equation N(α, n) + N(β, n) = n must agree if the equation is to hold for large n. Hence α and β are both rational or both irrational. If both are irrational, we do get a partition, as shown in the text. If both can be written with numerator m, the value m – 1 occurs in neither spectrum, and m occurs in both. (However, Golomb [151] has observed that the sets {nα | n ≥ 1} and {nβ – 1 | n ≥ 1} always do form a partition, when 1/α + 1/β = 1.)

3.14 It’s obvious by (3.22) if ny = 0, otherwise true by (3.21) and (3.6).

3.15 Plug in mx for n in (3.24): mx = x + x – + ··· + x – .

3.16 The formula n mod 3 = 1 + ((ω – 1)ωⁿ – (ω + 2)ω²ⁿ) can be verified by checking it when 0 ≤ n < 3.

A general formula for n mod m, when m is any positive integer, appears in exercise 7.25.

3.17 Σ_j,k[0 ≤ k < m][1 ≤ j ≤ x + k/m] = Σ_j,k[0 ≤ k< m][1 ≤ j ≤ x] × [k ≥ m(j – x)] = Σ_1≤j≤x Σ_k[0 ≤ k < m] – Σ_j=x Σ_k [0 ≤ k < m(j – x)] = mx – m(x – x) = ––mx = mx.

3.18 We have

If j ≤ nα – 1 ≤ nα – v, there is no contribution, because (j + v)α^–1 ≤ n. Hence j = nα is the only case that matters, and the value in that case equals (nα + v)α^–1 – n ≤ vα^–1.

3.19 If and only if b is an integer. (If b is an integer, log_b x is a continuous, increasing function that takes integer values only at integer points. If b is not an integer, the condition fails when x = b.)

3.20 We have ∑_k kx[α ≤ kx ≤ β] = x ∑_k k[α/x ≤ k ≤ β/x], which sums to x(β/x β/x + 1 – α/x α/x – 1).

3.21 If 10ⁿ ≤ 2^M < 10ⁿ⁺¹, there are exactly n+1 such powers of 2, because there’s exactly one such k-digit power of 2 for each k. Therefore the answer is 1 + M log 2.

Note: The number of powers of 2 with leading digit l is more difficult, when l > 1; it’s ∑_0≤n≤M (n log 2 – log l – n log 2 – log(l + 1)).

3.22 All terms are the same for n and n–1 except the kth, where n = 2^k–1q and q is odd; we have S_n = S_n–1 + 1 and T_n = T_n–1 + 2^kq. Hence S_n = n and T_n = n(n + 1).

3.23 X_n = m ⇔ m(m – 1) < n ≤ m(m + 1) ⇔ m² – m + < 2n < m² + m + ⇔ m – < < m + .

3.24 Let β = α/(α + 1). Then the number of times the nonnegative integer m occurs in Spec(β) is exactly one more than the number of times it occurs in Spec(α). Why? Because N(β, n) = N(α, n) + n + 1.

3.25 Continuing the development in the text, if we could find a value of m such that K_m ≤ m, we could violate the stated inequality at n + 1 when n = 2m + 1. (Also when n = 3m + 1 and n = 3m + 2.) But the existence of such an m = n′ + 1 requires that 2K_n′/2 ≤ n′ or 3K_n′/3 ≤ n′, i.e., that

K_n′/2 ≤ n′/2    or    K_n′/3 ≤ n′/3.

Aha. This goes down further and further, implying that K₀ ≤ 0; but K₀ = 1.

What we really want to prove is that K_n is strictly greater than n, for all n ≥ 0. In fact, it’s easy to prove this by induction, although it’s a stronger result than the one we couldn’t prove!

(This exercise teaches an important lesson. It’s more an exercise about the nature of induction than about properties of the floor function.)

“In trying to devise a proof by mathematical induction, you may fail for two opposite reasons. You may fail because you try to prove too much: Your P(n) is too heavy a burden. Yet you may also fail because you try to prove too little: Your P(n) is too weak a support. In general, you have to balance the statement of your theorem so that the support is just enough for the burden.”

—G. Pólya [297]

3.26 Induction, using the stronger hypothesis

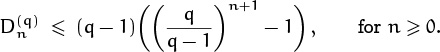
3.27 If = 2^mb – a, where a is 0 or 1, then = 3^mb – a.

3.28 The key observation is that a_n = m² implies a_n+2k+1 = (m + k)² + m–k and a_n+2k+2 = (m+k)²+2m, for 0 ≤ k ≤ m; hence a_n+2m+1 = (2m)². The solution can be written in a nice form discovered by Carl Witty:

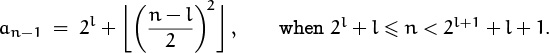
3.29 D(α′, αn) is at most the maximum of the absolute value of s(α′, nα, v′) = –s(α, n, v) – S + + {0 or 1} + v′ – {0 or 1}.

3.30 X_n = α²ⁿ + α^–2n, by induction; and X_n is an integer.

This logic is seriously floored.

3.31 Here’s an “elegant,” “impressive” proof that gives no clue about how it was discovered:

x + y + x + y	=	x + y + x + y
	≤	x + 2y + x + 2y +
	=	2x + 2y = 2x + 2y.

But there’s also a simple, graphical proof based on the observation that we need to consider only the case 0 ≤ x, y < 1. Then the functions look like this in the plane:

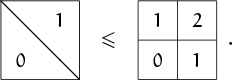
A slightly stronger result is possible, namely

x + y + x + y ≤ 2x + 2y;

but this is stronger only when . If we replace (x, y) by (–x, x + y) in this identity and apply the reflective law (3.4), we get

y + x + y + 2x ≤ x + 2x + 2y.

3.32 Let f(x) be the sum in question. Since f(x) = f(–x), we may assume that x ≥ 0. The terms are bounded by 2^k as k → –∞ and by x²/2^k as k → +∞, so the sum exists for all real x.

We have f(2x) = 2 ∑_k 2^k–1∥x/2^k–1∥² = 2f(x). Let f(x) = l(x) + r(x) where l(x) is the sum for k ≤ 0 and r(x) is the sum for k > 0. Then l(x + 1) = l(x), and l(x) ≤ 1/2 for all x. When 0 ≤ x < 1, we have r(x) = x²/2 + x²/4 + · · · = x², and r(x + 1) = (x – 1)²/2 + (x + 1)²/4 + (x + 1)²/8 + · · · = x² + 1. Hence f(x + 1) = f(x) + 1, when 0 ≤ x < 1.

We can now prove by induction that f(x + n) = f(x) + n for all integers n ≥ 0, when 0 ≤ x < 1. In particular, f(n) = n. Therefore in general, f(x) = 2^–mf(2^mx) = 2^–m2^mx + 2^–mf ({2^mx}). But f({2^mx}) = l({2^mx}) + r({2^mx}) ≤ + 1; so |f(x) – x| ≤ |2^–m 2^mx – x| + 2^–m· ≤ 2^–m · for all integers m.

The inescapable conclusion is that f(x) = |x| for all real x.

3.33 Let r = n – be the radius of the circle. (a) There are 2n–1 horizontal lines and 2n–1 vertical lines between cells of the board, and the circle crosses each of these lines twice. Since r² is not an integer, the Pythagorean theorem tells us that the circle doesn’t pass through the corner of any cell. Hence the circle passes through as many cells as there are crossing points, namely 8n – 4 = 8r. (The same formula gives the number of cells at the edge of the board.) (b) f(n,k) = 4.

It follows from (a) and (b) that

The task of obtaining more precise estimates of this sum is a famous problem in number theory, investigated by Gauss and many others; see Dickson [78, volume 2, chapter 6].

3.34 (a) Let m = lg n. We can add 2^m – n terms to simplify the calculations at the boundary:

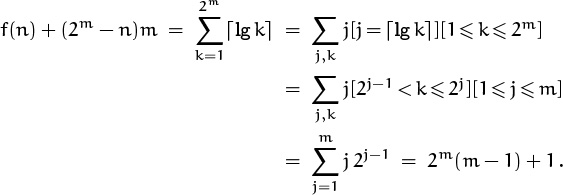
Consequently f(n) = nm – 2^m + 1.

(b) We have n/2 = (n+1)/2, and it follows that the solution to the general recurrence g(n) = a(n) + g (n/2) + g(n/2) must satisfy Δg(n) = Δa(n)+Δg (n/2). In particular, when a(n) = n–1, Δf(n) = 1+Δf (n/2) is satisfied by the number of bits in the binary representation of n, namely lg(n + 1). Now convert from Δ to Σ.

A more direct solution can be based on the identities lg 2j = lg j + 1 and lg(2j – 1) = lg j + [j > 1], for j ≥ 1.

3.35 (n + 1)²n!e = A_n + (n + 1)² + (n + 1) + B_n, where

is a multiple of n and

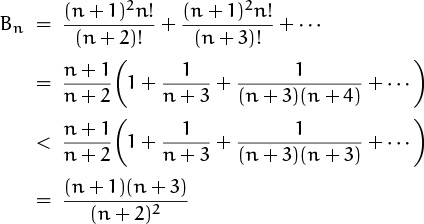
is less than 1. Hence the answer is 2 mod n.

3.36 The sum is

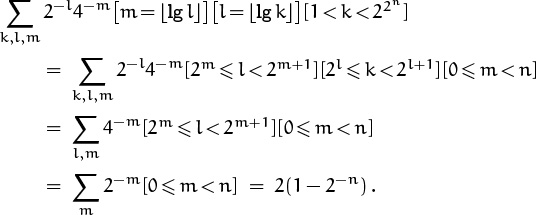
3.37 First consider the case m < n, which breaks into subcases based on whether ; then show that both sides change in the same way when m is increased by n.

This is really only a level 4 problem, in spite of the way it’s stated.

3.38 At most one x_k can be noninteger. Discard all integer x_k, and suppose that n are left. When {x} ≠ 0, the average of {mx} as m → ∞ lies between and ; hence {mx₁} + · · · + {mx_n} – {mx₁ + · · · + mx_n} cannot have average value zero when n > 1.

But the argument just given relies on a difficult theorem about uniform distribution. An elementary proof is possible, sketched here for n = 2: Let P_m be the point ({mx}, {my}). Divide the unit square 0 ≤ x, y < 1 into triangular regions A and B according as x + y < 1 or x + y ≥ 1. We want to show that P_m ∈ B for some m, if {x} and {y} are nonzero. If P₁ ∈ B, we’re done. Otherwise there is a disk D of radius > 0 centered at P₁ such that D ⊆ A. By Dirichlet’s box principle, the sequence P₁, . . . , P_N must contain two points with |P_k – P_j| < and k > j, if N is large enough.

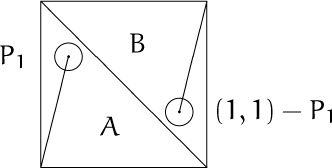
It follows that P_k–j–1 is within of (1, 1) – P₁; hence P_k–j–1 ∈ B.

3.39 Replace j by b – j and add the term j = 0 to the sum, so that exercise 15 can be used for the sum on j. The result,

x/b^k – x/b^k+1 + b – 1,

telescopes when summed on k.

3.40 Let 2 = 4k + r where –2 ≤ r < 2, and let m = . Then the following relationships can be proved by induction:

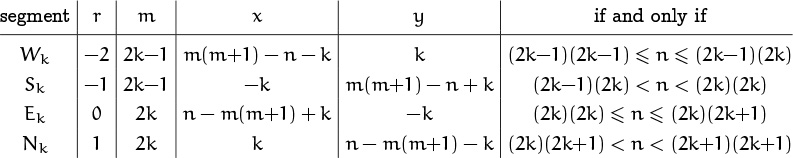
Thus, when k ≥ 1, W_k is a segment of length 2k – 1 where the path travels west and y(n) = k; S_k is the interior of a segment of length 2k where the path travels south and x(n) = –k; etc. (a) The desired formula is therefore

y(n) = (–1)^m((n – m(m + 1))·[2 is odd] – m).

(b) On all segments, k = max(|x(n)|, |y(n)|). On segments W_k and S_k we have x < y and n + x + y = m(m + 1) = (2k)² – 2k; on segments E_k and N_k we have x ≥ y and n – x – y = m(m + 1) = (2k)² + 2k. Hence the sign is (–1)^[x(n)<y(n)].

3.41 Since 1/ϕ + 1/ϕ² = 1, the stated sequences do partition the positive integers. Since the condition g(n) = f(f(n)) + 1 determines f and g uniquely, we need only show that nϕϕ + 1 = nϕ² for all n > 0. This follows from exercise 3, with α = ϕ and n = 1.

3.42 No; an argument like the analysis of the two-spectrum case in the text and in exercise 13 shows that a tripartition occurs if and only if 1/α + 1/β + 1/γ = 1 and

for all n > 0. But the average value of {(n + 1)/α} is 1/2 if α is irrational, by the theorem on uniform distribution. The parameters can’t all be rational, and if γ = m/n the average is 3/2 – 1/(2n). Hence γ must be an integer, but this doesn’t work either. (There’s also a proof of impossibility that uses only simple principles, without the theorem on uniform distribution; see [155].)

3.43 One step of unfolding the recurrence for K_n gives the minimum of the four numbers 1 + a + a · b · K_{(n–1–a)/(a·b)}, where a and b are each 2 or 3. (This simplification involves an application of (3.11) to remove floors within floors, together with the identity x + min(y, z) = min(x + y, x + z). We must omit terms with negative subscripts; i.e., with n – 1 – a < 0.)

Continuing along such lines now leads to the following interpretation: K_n is the least number > n in the multiset S of all numbers of the form

1 + a₁ + a₁a₂ + a₁a₂a₃ + · · · + a₁a₂a₃ . . . a_m ,

where m ≥ 0 and each a_k is 2 or 3. Thus,

S = {1, 3, 4, 7, 9, 10, 13, 15, 19, 21, 22, 27, 28, 31, 31, . . . };

the number 31 is in S “twice” because it has two representations 1 + 2 + 4 + 8 + 16 = 1 + 3 + 9 + 18. (Incidentally, Michael Fredman [134] has shown that lim_n→∞ K_n/n = 1, i.e., that S has no enormous gaps.)

3.44 Let mumble(q–1), so that and . Now , and the results follow. (This is the solution found by Euler [116], who determined the a’s and d’s sequentially without realizing that a single sequence would suffice.)

Too easy.

3.45 Let α > 1 satisfy α + 1/α = 2m. Then we find 2Y_n = α²ⁿ + α^–2n, and it follows that Y_n = α²ⁿ/2.

3.46 The hint follows from (3.9), since 2n(n + 1) = 2(n + )². Let n + θ = (^l + ^l–l)m and n′ + θ′ = (^l+1 + ^l)m, where 0 ≤ θ, θ′ < 1. Then θ′ = 2θ mod 1 = 2θ – d, where d is 0 or 1. We want to prove that n′ = (n + ); this equality holds if and only if

0 ≤ θ′(2 – ) + (1 – d) < 2.

To solve the recurrence, note that Spec(1 + 1/) and Spec(1 + ) partition the positive integers; hence any positive integer a can be written uniquely in the form a = (^l + ^l–1)m, where l and m are integers with m odd and l ≥ 0. It follows that L_n = (^l+n + ^l+n–1)m.

3.47 (a) . (b) c is an integer. (c) c = 0. (d) c is arbitrary. See the answer to exercise 1.2.4–40 in [207] for more general results.

3.48 Let x^:0 = 1 and x^:(k+1) = xx^:k; also let a_k = {x^:k} and b_k = x^:k, so that the stated identity reads x³ = 3x^:3 + 3a₁a₂ + – 3b₁b₂ + . Since a_k + b_k = x^:k = xb_k–1 for k ≥ 0, we have (1 – xz)(1 + b₁z + b₂z² + · · ·) = 1 – a₁z – a₂z² – · · · ; thus

Take the logarithm of both sides, to separate the a’s from the b’s. Then differentiate with respect to z, obtaining

The coefficient of z^n–1 on the left is xⁿ; on the right it is a formula that matches the given identity when n = 3.

Similar identities for the more general product x₀x₁ . . . x_n–1 can also be derived [170].

3.49 (Solution by Heinrich Rolletschek.) We can replace (α, β) by ({β}, α + β) without changing nα + nβ. Hence the condition α = {β} is necessary. It is also sufficient: Let m = β be the least element of the given multiset, and let S be the multiset obtained from the given one by subtracting mn from the nth smallest element, for all n. If α = {β}, consecutive elements of S differ by either 0 or 2, hence the multiset S = Spec(α) determines α.

A more interesting (still unsolved) problem: Restrict both α and β to be < 1, and ask when the given multiset determines the unordered pair {α, β}.

3.50 According to unpublished notes of William A. Veech, it is sufficient to have αβ, β, and 1 linearly independent over the rationals.

3.51 H. S. Wilf observes that the functional equation f(x²–1) = f(x)² would determine f(x) for all x ≥ ϕ if we knew f(x) on any interval (ϕ . . ϕ + ).

3.52 There are infinitely many ways to partition the positive integers into three or more generalized spectra with irrational α_k; for example,

Spec(2α; 0) ∪ Spec(4α; – α) ∪ Spec(4α; – 3α) ∪ Spec(β; 0)

works. But there’s a precise sense in which all such partitions arise by “expanding” a basic one, Spec(α) ∪ Spec(β); see [158]. The only known rational examples, e.g.,

Spec(7; – 3) ∪ Spec(; – 1) ∪ Spec(; 0) ,

are based on parameters like those in the stated conjecture, which is due to A. S. Fraenkel [128].

3.53 Partial results are discussed in [95, pages 30–31]. The greedy algorithm probably does not terminate.

4.1 1, 2, 4, 6, 16, 12.

4.2 Note that m_p + n_p = min(m_p, n_p) + max(m_p, n_p). The recurrence lcm(m, n) = (n/(n mod m)) lcm(n mod m, m) is valid but not really advisable for computing lcm’s; the best way known to compute lcm(m, n) is to compute gcd(m, n) first and then to divide mn by the gcd.

4.3 This holds if x is an integer, but π(x) is defined for all real x. The correct formula,

π(x) – π(x – 1) = [x is prime] ,

is easy to verify.

4.4 Between and we’d have a left-right reflected Stern–Brocot tree with all denominators negated, etc. So the result is all fractions m/n with m ⊥ n. The condition m′n–mn′ = 1 still holds throughout the construction. (This is called the Stern–Brocot wreath, because we can conveniently regard the final as identical to the first , thereby joining the trees in a cycle at the top. The Stern–Brocot wreath has interesting applications to computer graphics because it represents all rational directions in the plane.)

4.5 and ; this holds even when k < 0. (We will find a general formula for any product of L’s and R’s in Chapter 6.)

After all, ‘mod y’ sort of means “pretend y is zero.” So if it already is, there’s nothing to pretend.

4.6 a = b. (Chapter 3 defined x mod 0 = x, primarily so that this would be true.)

4.7 We need m mod 10 = 0, m mod 9 = k, and m mod 8 = 1. But m can’t be both even and odd.

4.8 We want 10x + 6y ≡ 10x + y (mod 15); hence 5y ≡ 0 (mod 15); hence y ≡ 0 (mod 3). We must have y = 0 or 3, and x = 0 or 1.

4.9 3^2k+1 mod 4 = 3, so (3^2k+1 – 1)/2 is odd. The stated number is divisible by (3⁷ – 1)/2 and (3¹¹ – 1)/2 (and by other numbers).

4.10 .

4.11 σ(0) = 1; σ(1) = –1; σ(n) = 0 for n > 1. (Generalized Möbius functions defined on arbitrary partially ordered structures have interesting and important properties, first explored by Weisner [366] and developed by many other people, notably Gian-Carlo Rota [313].)

4.12 ∑_dm ∑_kd μ(d/k) g(k) = ∑_km ∑_d(m/k) μ(d) g(k) = ∑_kmg(k)×[m/k = 1] = g(m), by (4.7) and (4.9).

4.13 (a) n_p ≤ 1 for all p; (b) μ(n) ≠ 0.

4.14 True when k > 0. Use (4.12), (4.14), and (4.15).

4.15 No. For example, e_n mod 5 = [2 or 3]; e_n mod 11 = [2, 3, 7, or 10].

4.16 1/e₁ + 1/e₂ + · · · + 1/e_n = 1 – 1/(e_n(e_n – 1)) = 1 – 1/(e_n+1 – 1).

4.17 We have f_n mod f_m = 2; hence gcd(f_n, f_m) = gcd(2, f_m) = 1. (Incidentally, the relation f_n = f₀f₁ . . . f_n–1 + 2 is very similar to the recurrence that defines the Euclid numbers e_n.)

4.18 If n = qm and q is odd, 2ⁿ+1 = (2^m+1)(2^n–m –2^n–2m +· · ·–2^m+1).

4.19 The first sum is π(n), since the summand is [k + 1 is prime]. The inner sum in the second is ∑_1≤k<m[km], so it is greater than 1 if and only if m is composite; again we get π(n). Finally , so the third sum is an application of Wilson’s theorem. To evaluate π(n) by any of these formulas is, of course, sheer lunacy.

4.20 Let p₁ = 2 and let p_n be the smallest prime greater than 2^p_n–1. Then 2^p_n–1 < p_n < 2^p_n–1 +1, and it follows that we can take b = lim_n→∞ lg⁽ⁿ⁾ p_n where lg⁽ⁿ⁾ is the function lg iterated n times. The stated numerical value comes from p₂ = 5, p₃ = 37. It turns out that p₄ = 2³⁷ + 9, and this gives the more precise value

b ≈ 1.2516475977905

(but no clue about p₅).

4.21 By Bertrand’s postulate, P_n < 10ⁿ. Let

Then 10ⁿ²K ≡ P_n + fraction (mod 10^2n–1).

4.22 (b^mn – 1)/(b – 1) = ((b^m – 1)/(b – 1)) (b^{mn –m} + · · · + 1). [The only prime numbers of the form (10^p – 1)/9 for p < 49081 occur when p = 2, 19, 23, 317, 1031.] Numbers of this form are called “repunits.”

4.23 ρ(2k + 1) = 0; ρ(2k) = ρ(k) + 1, for k ≥ 1. By induction we can show that ρ(n) = ρ(n – 2^m), if n > 2^m and m > ρ(n). The kth Hanoi move is disk ρ(k), if we number the disks 0, 1, . . . , n – 1. This is clear if k is a power of 2. And if 2^m < k < 2^m+1, we have ρ(k) < m; moves k and k – 2^m correspond in the sequence that transfers m + 1 disks in T_m + 1 + T_m steps.

4.24 The digit that contributes dp^m to n contributes dp^m–1 + · · · + d = d(p^m – 1)/(p – 1) to _p(n!), hence _p(n!) = (n – ν_p(n))/(p – 1).

4.25 m\n ⇔ m_p = 0 or m_p = n_p, for all p. It follows that (a) is true. But (b) fails, in our favorite example m = 12, n = 18. (This is a common fallacy.)

4.26 Yes, since defines a subtree of the Stern–Brocot tree.

4.27 Extend the shorter string with M’s (since M lies alphabetically between L and R) until both strings are the same length, then use dictionary order. For example, the topmost levels of the tree are LL < LM < LR < MM < RL < RM < RR. (Another solution is to append the infinite string RL^∞ to both inputs, and to keep comparing until finding L < R.)

4.28 We need to use only the first part of the representation:

The fraction appears because it’s a better upper bound than , not because it’s closer than . Similarly, is a better lower bound than . The simplest upper bounds and the simplest lower bounds all appear, but the next really good approximation doesn’t occur until just before the string of R’s switches back to L.

4.29 1/α. To get 1 – x from x in binary notation, we interchange 0 and 1; to get 1/α from α in Stern–Brocot notation, we interchange L and R. (The finite cases must also be considered, but they must work since the correspondence is order preserving.)