8
FREQUENCY RESPONSE ANALYSIS
8.1 Introduction
After obtaining the mathematical model of the system, its performance is analysed based on the time response or frequency response. Time response of the system is defined as the response of the system when standard test signals such as impulse, step and so on are applied to it. Frequency response of the system is defined as the response of the system when standard sinusoidal signals are applied to it with constant amplitude over a range of frequencies. The frequency response indicates the steady-state response of a system to a sinusoidal input. The characteristics and performance of the industrial control system are analysed by using the frequency response techniques. Frequency response analysis is used in numerous systems and components such as audio and video amplifiers, speakers, sound cards and servomotors. The different techniques available for frequency response analysis lend themselves to a simplest procedure for experimental testing and analysis. In addition, the stability and relative stability of the system for the sinusoidal input can be analysed by using different frequency plots.
This chapter introduces the frequency response of the system and explains the procedure for construction of Bode plot to determine frequency domain specifications such as gain crossover frequency, phase crossover frequency, gain margin and phase margin.
8.1.1 Advantages of Frequency Response Analysis
The time response of the system can be obtained only if the transfer function of the system is known earlier, which is always not possible. But it is possible to obtain frequency response of the system even though the transfer function of the system is not known. The reasons for determining the frequency response of the system are:
- Analytically, it is more difficult to determine the time response of the system for higher order systems.
- As there exists numerous ways of designing a control system to meet the time domain performance specifications, it becomes difficult for the designer to choose a suitable design for a particular system.
- The transfer function of a higher order system can be identified by computing the frequency response of the system over a wide range of frequencies
 .
. - The time-domain specifications of a system can be met by using the frequency domain specifications as a correlation exists between the frequency response and time response of a system.
- The stability of a non-linear system can be analysed by the frequency response analysis.
- The transfer function of a higher order system can be obtained using frequency response analysis which makes use of physical data when it is difficult to obtain using differential equations.
- The frequency response analysis can be applied to the system that has no rational transfer function (i.e., a system with transportation lag).
- The frequency response analysis can be applied to the system even when the input is not deterministic.
- The frequency response analysis is very convenient in measuring the system sensitivity to noise and parameter variations.
- In frequency response analysis, stability and relative stability of a system can be analysed without evaluating the roots of the characteristic equation of the system.
- The frequency response analysis is simple and accurate.
8.1.2 Disadvantages of Frequency Response Analysis
The disadvantages of frequency response analysis are:
- Frequency response analysis is not recommended for the system with very large time constants.
- It is not useful for non-interruptible systems.
- It can generally be applied only to linear systems. When this approach is applied to a non-linear system, the result obtained is not exact.
- It is considered as outdated when compared with the methods developed for digital computer and modelling.
The comparison between the time response analysis and frequency response analysis is listed in Table 8.1.
Table 8.1 ∣ Comparison between the time response analysis and frequency response analysis

8.2 Importance of Sinusoidal Waves for Frequency Response Analysis
In frequency response analysis, the signal used as an input to the system is a sinusoidal wave because of the following reasons:
- Fourier theory (infinite sum of sine wave and cosine wave).
- Any input signal applied to the circuit can be represented as a combination of sine and cosine waves of different frequencies and amplitudes.
Consider a ramp signal as shown in Fig. 8.1(a) and constant sine and cosine waves of varying amplitude as shown in Fig. 8.1(b).

Fig. 8.1 ∣ (a) Ramp signal, (b) Fourier components and (c) original and sum of fourier components
If the sine wave and cosine wave as shown in Fig. 8.1(b) are added, the resultant will be a ramp signal indicated using a dotted line along with the original ramp signal shown as a continuous line depicted in Fig. 8.1(c). Since any signal can be represented by varying the frequency and amplitude of the sine and cosine waves, the sinusoidal wave is chosen for frequency domain analysis.
8.3 Basics of Frequency Response Analysis
The steady-state output of the stable linear system is also a sine wave of same frequency when a sinusoidal input is applied to the system. The output and input of the system generally differs in both magnitude and phase. Generally, the frequency response of the system can be obtained by replacing the variable s in the transfer function with ![]() as given by
as given by
![]() (8.1)
(8.1)
where ![]() is the magnitude or gain i.e., the sinusoidal amplitude ratio of output to input. In addition,
is the magnitude or gain i.e., the sinusoidal amplitude ratio of output to input. In addition, ![]() is the angle by which the output leads the input. The parameters
is the angle by which the output leads the input. The parameters ![]() and
and ![]() are functions of the angular frequency
are functions of the angular frequency ![]() . The Laplace variable s is a complex number that is represented as
. The Laplace variable s is a complex number that is represented as ![]() . If a linear time-invariant system is subjected to a pure sinusoidal input,
. If a linear time-invariant system is subjected to a pure sinusoidal input, ![]() , the output response of the system contains both the transient part and the steady-state part. But at
, the output response of the system contains both the transient part and the steady-state part. But at ![]() , the transient part dies out because the roots have negative parts for a stable system and only the steady-state part of the output response exists. Therefore, as the frequency response of the system deals with steady-state analysis of the system, it is enough to substitute
, the transient part dies out because the roots have negative parts for a stable system and only the steady-state part of the output response exists. Therefore, as the frequency response of the system deals with steady-state analysis of the system, it is enough to substitute ![]() instead of
instead of ![]() .
.
Example 8.1 Consider a low-pass RC network with ![]() and
and ![]() as shown in Fig. E8.1 and is driven by the input voltage
as shown in Fig. E8.1 and is driven by the input voltage ![]() Determine the output voltage v0(t) across the capacitor, C.
Determine the output voltage v0(t) across the capacitor, C.

Fig. E8.1
Solution: The transfer function of the low-pass RC network is

Substituting the values of ![]() and
and ![]() , we obtain
, we obtain
![]()
The Laplace transform of the input, ![]()
Hence, the output of the system, 
Using partial fractions, we obtain 
Taking inverse Laplace transform, we obtain ![]()
where ![]() is the transient part of the output and
is the transient part of the output and ![]() is the steady-state part of the output.
is the steady-state part of the output.
8.4 Frequency Response Analysis of Open-Loop and Closed-Loop Systems
The frequency response analysis of both open-loop and closed-loop systems is discussed below.
8.4.1 Open-Loop System
Fig. 8.2 ∣ A simple open-loop system
Consider an open-loop linear time-invariant system as shown in Fig. 8.2. The input signal i.e., sinusoidal with amplitude ![]() and frequency
and frequency ![]() is given by
is given by
![]()
The steady-state output of the system ![]() will also be a sinusoidal function with the same frequency
will also be a sinusoidal function with the same frequency ![]() but possibly with a different amplitude and phase, i.e.,
but possibly with a different amplitude and phase, i.e.,
![]()
where ![]() is the amplitude of the output sinusoidal wave and
is the amplitude of the output sinusoidal wave and ![]() is the phase shift in degrees or radians.
is the phase shift in degrees or radians.
Let the transfer function of a linear single-input single-output (SISO) system be ![]() . Then, the relation between the Laplace transforms of the input and the output is
. Then, the relation between the Laplace transforms of the input and the output is
![]()
For sinusoidal steady-state analysis i.e., frequency response analysis, s is replaced with ![]() Then, the above equation becomes
Then, the above equation becomes
![]() (8.2)
(8.2)
Here, ![]() can be written in terms of magnitude and phase angle as
can be written in terms of magnitude and phase angle as
![]() (8.3)
(8.3)
Similarly, Eqn. (8.2) can be re-written as
![]() (8.4)
(8.4)
Hence, comparing Eqs. (8.3) and (8.4), we obtain
![]() (8.5)
(8.5)
and the phase angle is
![]() (8.6)
(8.6)
From the transfer function ![]() of a linear time-invariant system with sinusoidal input, the magnitude and phase angle of the output can be obtained using Eqs. (8.5) and (8.6) respectively.
of a linear time-invariant system with sinusoidal input, the magnitude and phase angle of the output can be obtained using Eqs. (8.5) and (8.6) respectively.
8.4.2 Closed-Loop System

Fig. 8.3 ∣ A simple closed-loop system
The closed-loop system is shown in Fig. 8.3.
The transfer function 
For the frequency response analysis, substituting ![]() , we get
, we get

The transfer function ![]() can be expressed in terms of its magnitude and phase as
can be expressed in terms of its magnitude and phase as
![]()
Therefore, the magnitude of ![]() is
is
 (8.7)
(8.7)
The phase angle of ![]() is
is
![]() (8.8)
(8.8)
Thus, by knowing the transfer function ![]() of a linear time-invariant system and the feedback transfer function
of a linear time-invariant system and the feedback transfer function ![]() the magnitude and phase angle of the output for the closed-loop system can be obtained using Eqs. (8.7) and (8.8) respectively, provided the input to the system is sinusoidal.
the magnitude and phase angle of the output for the closed-loop system can be obtained using Eqs. (8.7) and (8.8) respectively, provided the input to the system is sinusoidal.
8.4.3 Closed-Loop System with Poles and Zeros
Consider a negative feedback closed-loop system as shown in Fig. 8.3 with the closed-loop transfer function as
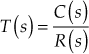 (8.9)
(8.9)
where ![]() is the Laplace transform of the output and
is the Laplace transform of the output and ![]() is the Laplace transform of the input.
is the Laplace transform of the input.
For a closed-loop stable system,
 (8.10)
(8.10)
where, ![]() and
and ![]()
where ![]() and
and ![]() are positive and distinct integers with
are positive and distinct integers with ![]() .
.
Consider the input ![]() applied to the system as
applied to the system as

Taking Laplace transform, we obtain ![]()
Hence, the Laplace transform of the output using Eqn. (8.9) is ![]()
Substituting Eqn. (8.10) in the above equation, we obtain

Using partial fractions for the above equation, we obtain

 (8.11)
(8.11)
Here, ![]() , where
, where ![]()
In addition, ![]()
![]()

![]()
As the constant K1 is a complex number, it is convenient to represent it in polar form as
![]() where
where ![]()


![]()
Since we have assumed all the values of ![]() the steady-state response is
the steady-state response is
![]()
Thus, if a sinusoidal input is applied to a system that has negative real value of poles, the steady-state response is a scaled, phase-shifted version of the input. The scaling factor is ![]() and the phase shift
and the phase shift ![]() is the phase of
is the phase of ![]() .
.
8.5 Frequency Response Representation
The frequency response analysis of a system is used to determine the system gain and phase angle of the system at different frequencies. Hence, the system gain and phase angle can be represented either in a tabular form or graphical form.
Tabular form: It is useful in representing the system gain and phase angle of a system at different frequencies only if the data set is relatively small. It is also useful in experimental measurement.
Graphical form: It provides a convenient way to view the frequency response data. There are many ways of representing the frequency response in the graphical form.
8.5.1 Determination of Frequency Response
The frequency response analysis of a system can be determined using (i) experimental determination and (ii) mathematical determination.
(i) Experimental determination of frequency response
This method is used only when the system transfer function is not known. This method is used for a plant testing and verification of the plant model. Determining the frequency response of a the small system experimentally in a laboratory environment is not very difficult. A typical set-up for the experimental determination of the frequency response is shown in Fig. 8.4.

Fig. 8.4 ∣ Experimental set-up for frequency response
The requirement for determining frequency response varies for different systems. The general requirements for determining the frequency response of systems are power supply, signal generator and a chart recorder or dual trace oscilloscope. The experimental set-up varies depending on the test systems.
The steps to be followed for determining the frequency response are:
- Test frequency range and input signal amplitude are established.
- Sinusoidal signal with low frequency is applied and sufficient time is allowed for settling of transients present in the system.
- After a stable output is reached, using the input and output waveforms, the system gain and phase angle are determined.
- The same procedure can be applied for the input signal with different frequencies and the frequency response analysis of the system can be determined.
Thus, the frequency response of the system whose transfer function is not known can be determined.
Mathematical evaluation of frequency response
This method is applicable to the system whose transfer function is known. In this method, by substituting ![]() , the transfer function is considered to be a function of frequency and it is treated as a complex variable. The system gain and phase angle at a particular frequency is same as the magnitude and phase angle of the complex number.
, the transfer function is considered to be a function of frequency and it is treated as a complex variable. The system gain and phase angle at a particular frequency is same as the magnitude and phase angle of the complex number.
The mathematical procedure for determining the frequency response of simple and complex transfer functions are given below:
Simple transfer function
- Choose the frequency for which the frequency response has to be determined.
- Substitute
 in the given transfer function.
in the given transfer function. - Convert the resultant complex number into a polar form.
- Substitute the chosen frequency
 in the above equation and determine the magnitude and angle of the complex number.
in the above equation and determine the magnitude and angle of the complex number. - Then, the system gain and phase angle at that particular frequency are determined.
- Repeat the above steps for different frequencies and the corresponding system gain and the phase angle can be tabulated.
Complex transfer function
A complex transfer function can be separated in two simple transfer functions and each simple transfer function can be converted into the polar form. The complex number in polar form allows easier manipulation of magnitude and angle. The procedure is as follows:
- Convert the complex transfer function into a product of simple transfer functions.
- For each simple transfer function, follow the steps that have been discussed earlier to determine the individual magnitude and angle of the simple transfer functions.
- Then, the overall gain and phase angle of the complex transfer function at a particular frequency can be obtained by multiplying the individual gain and adding the phase angles, respectively.
- The above steps can be repeated for different frequencies and the system gain and phase angle can be determined.
Example 8.2 The transfer function of the system is given by  . Determine the frequency response of the system over a frequency range of 0.1–10 rad/sec.
. Determine the frequency response of the system over a frequency range of 0.1–10 rad/sec.
Solution:
Gain of the complex system = product of gains of simple systems
Phase angle of the complex system = addition of phase angles of simple systems
The given complex system can be divided into four simple functions as
![]()
Simple system 1:
![]()
Substituting ![]() , we obtain
, we obtain ![]()
Therefore, gain of the system M1 = 5 and phase angle of the system ![]() = 0°.
= 0°.
Simple system 2
![]()
Substituting ![]() , we obtain
, we obtain ![]()
Therefore, gain of the system M2 = ![]() and phase angle of the system
and phase angle of the system ![]()
Simple system 3
![]()
Substituting ![]() , we obtain
, we obtain ![]()
Therefore, gain of the system, M3 = 
and phase angle of the system ![]()
![]()
Simple system 4
![]()
Therefore, ![]()
Therefore, gain of the system ![]()

and phase angle of the system ![]()
The gain and the phase angle of various simple systems at different frequencies between 0.1 and 10 rad/sec are calculated and tabulated as given in Tables E8.3(a) and (b) respectively.
Table E8.3(a) ∣ Gain of the simple systems at different frequencies

Table E8.3(b) ∣ Phase angle of the system at different frequencies

Therefore, the overall gain and phase angle of the complex system is determined using the following expressions and are tabulated in Table E8.3(c).
Gain of the system, ![]()
Phase angle of the system, ![]() .
.
Table E8.3(c) ∣ Gain and phase angle of the complex system at different frequencies

8.6 Frequency Domain Specifications
Frequency domain specifications of a system are necessary to determine the quality of the system and to design the linear control systems using frequency domain analysis.
Consider a simple closed-loop system as shown in Fig. 8.3. Its transfer function is

The magnitude or gain of the above transfer function as a function of frequency is given by

The phase angle of the transfer function as a function of frequency is given by
![]()
The typical gain–phase characteristics of a feedback control system are shown in Figs. 8.5(a) and (b).

Fig. 8.5 ∣ Gain–phase characteristics
The different frequency domain specifications that are required for designing a control system and determining its performance are:
(i) Resonant peak Mr
The maximum value of gain ![]() as the frequency of the system
as the frequency of the system ![]() is varied over a range is known as resonant peak
is varied over a range is known as resonant peak ![]() . The relative stability of the system can be determined based on this value. There exists a direct relationship between the maximum overshoot in the time-domain analysis of the system and the resonant peak in the frequency domain analysis (i.e., a large value of
. The relative stability of the system can be determined based on this value. There exists a direct relationship between the maximum overshoot in the time-domain analysis of the system and the resonant peak in the frequency domain analysis (i.e., a large value of ![]() indicates that the maximum overshoot of the system is also large). The resonant peak lies between 1.1 and 1.5.
indicates that the maximum overshoot of the system is also large). The resonant peak lies between 1.1 and 1.5.
(ii) Resonant frequency ![]()
The frequency of the system at which the resonant peak occurs is known as resonant frequency ![]() . The frequency of oscillations in the time domain is related to the resonant frequency
. The frequency of oscillations in the time domain is related to the resonant frequency ![]() . When resonant frequency is high, the time response or transient response of the system is fast.
. When resonant frequency is high, the time response or transient response of the system is fast.
(iii) Cut-off frequency ![]()
The frequency at which the gain of the system is 3 dB or 0.707 times the gain of the system at zero frequency is known as cut-off frequency ![]() .
.
(iv) Bandwidth
The range of frequencies that lie between zero and ![]() is known as bandwidth. It is also defined as the range of frequencies over which the magnitude response of the system is flat.
is known as bandwidth. It is also defined as the range of frequencies over which the magnitude response of the system is flat.
The value of bandwidth indicates the ability of the system to reproduce the input signal and it is a measure of the noise rejection characteristics. In time-domain analysis of the system for a given damping factor, bandwidth in the frequency domain indicates the rise time in the time domain. If the bandwidth of the system in the frequency domain is large, then the rise time of the system in time domain is small and the system will be faster.
(v) Cut-off rate
The slope of the magnitude curve obtained near the cut-off frequency is called cut-off rate. The cut-off rate indicates the ability of the system to distinguish the signal from noise.
(vi) Gain crossover frequency ![]()
The frequency at which the gain of the system is unity is called the gain crossover frequency ![]() .
.
If the gain of the system is expressed in dB, then the gain crossover frequency is defined as the frequency at which the gain of the system is 0 dB (since 20 log 1 = 0 dB).
(vii) Phase crossover frequency ![]()
The frequency at which the phase angle of the system is −180° is called phase crossover frequency.
(viii) Gain margin gm
In root locus technique, there exists a relationship between the gain and stability of the system. Similarly, in frequency response method, there exists a value of K, beyond which the system becomes unstable. Hence, the gain margin ![]() is defined as the factor by which the gain of the system can be increased before the system becomes unstable. Mathematically, it is defined as the reciprocal of the gain of the system at the phase crossover frequency
is defined as the factor by which the gain of the system can be increased before the system becomes unstable. Mathematically, it is defined as the reciprocal of the gain of the system at the phase crossover frequency ![]() .
.
The stability of the system is directly proportional to the gain margin of the system. In addition, the high gain margin results in an unacceptable response and the result becomes sluggish in nature.
(ix) Phase margin pm
In frequency response analysis, gain margin alone is not sufficient to comment on the relative stability of the system. The other factor that affects the relative stability of the system is phase margin ![]() . It is defined as the additional phase lag that makes the system marginally stable. In addition, it can be defined as the addition of phase angle of the system at gain crossover frequency and 180°.
. It is defined as the additional phase lag that makes the system marginally stable. In addition, it can be defined as the addition of phase angle of the system at gain crossover frequency and 180°.
As a thumb rule, for a good overall stability of the system, the gain margin of the system should be around 12 dB and the phase margin should be between 45° and 60°.
8.7 Frequency and Time Domain Interrelations
The interrelation between the time-domain analysis and frequency domain analysis of the system is explicit for the first order. In this section, the interrelation existing between the time domain and frequency domain for a second-order system is discussed. In addition, the frequency domain specifications for the second-order system are derived using the frequency response analysis.
Consider a second-order system as shown in Fig. 8.6 with the feed-forward transfer function as  and with a unity feedback.
and with a unity feedback.

Fig. 8.6 ∣ A simple second order system
Hence, the transfer function of the second-order system is given by
 (8.12)
(8.12)
where ![]() is the damping ratio of the system and
is the damping ratio of the system and ![]() is the undamped natural frequency of the system.
is the undamped natural frequency of the system.
In addition, ![]()
The transfer function of the system in frequency domain is obtained by substituting ![]() in Eqn. (8.12) given by
in Eqn. (8.12) given by
 (8.13)
(8.13)
Substituting ![]() in Eqn. (8.13), we obtain
in Eqn. (8.13), we obtain  (8.14)
(8.14)
where ![]() is the normalized driving signal frequency.
is the normalized driving signal frequency.
Therefore, ![]() (8.15)
(8.15)
Using Eqs. (8.14) and (8.15), we obtain  (8.16)
(8.16)
and ![]() (8.17)
(8.17)
The steady-state output of the system when the system is excited by the sinusoidal input with unit magnitude and variable frequency ![]() (i.e.,
(i.e., ![]() ) is given by
) is given by

Using Table 8.1, the magnitude and phase angle plots with respect to the normalized frequency u are shown in Figs. 8.7(a) and 8.7(b) respectively.
Table 8.2 ∣ Magnitude and phase values
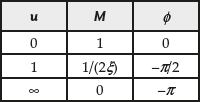

Fig. 8.7 ∣ (a) Magnitude and (b) phase angle plots of second-order system
8.7.1 Frequency Domain Specifications
(i) Resonant frequency ωr
At resonant frequency ![]() , the first-order derivative of the magnitude of frequency domain analysis is zero.
, the first-order derivative of the magnitude of frequency domain analysis is zero.
i.e., 
Since the magnitude in Eqn. (8.16) depends on the normalized frequency ![]() , the above equation can be written as
, the above equation can be written as 
where ![]() is the normalized resonant frequency.
is the normalized resonant frequency.
Therefore, 
Simplifying, we obtain ![]()
![]()
We know that, ![]() .
.
Therefore, the resonant frequency is given by ![]() (8.18)
(8.18)
(ii) Resonant peak Mr
The magnitude at resonant frequency ![]() , is known as the resonant peak
, is known as the resonant peak ![]() .
.
i.e., ![]()
Since the magnitude depends on the normalized frequency, the above equation can be written as
![]()
Substituting the ![]() in Eqs. (8.16) and (8.17), we obtain
in Eqs. (8.16) and (8.17), we obtain
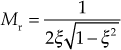 (8.19)
(8.19)
 (8.20)
(8.20)
But we know that in time domain analysis of a second-order system,
Peak overshoot, ![]() (8.21)
(8.21)
Damped natural frequency, ![]() (8.22)
(8.22)
From Eqs. (8.19) to (8.22), it is clear that there exists a relationship between the time-domain analysis and frequency domain analysis of a system.
Interesting facts about the interrelation between time-domain analysis and frequency domain analysis of a second-order system are given below.
- For relative stability of the system, the values of peak overshoot and resonant peak of the system are:
Peak overshoot

Resonant peak

If
 is greater than 1.5 and the system is subjected to noise signals, then the system may face serious problems.
is greater than 1.5 and the system is subjected to noise signals, then the system may face serious problems. - Variation of
 with respect to the variation in
with respect to the variation in 
- As
 increases, the value of peak overshoot,
increases, the value of peak overshoot,  gets decreased and it becomes zero or gets vanished at
gets decreased and it becomes zero or gets vanished at  .
.
The resonant peak
 will also get vanished as the damping ratio
will also get vanished as the damping ratio  increases. But the value of
increases. But the value of  at which the resonant peak vanishes is derived as
at which the resonant peak vanishes is derived as
Therefore,
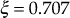
Hence, at
 , the resonant peak and peak overshoot vanished.
, the resonant peak and peak overshoot vanished.This concept is shown in Figs. 8.8(a) and (b).

Fig. 8.8 ∣ Mp and Mr for different values of

- When
 :
:
The
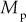 gets the maximum value i.e.,
gets the maximum value i.e.,  . In addition,
. In addition, 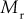 approaches infinity as
approaches infinity as  decreases to zero. This concept is shown in Figs. 8.9(a) and (b) respectively.
decreases to zero. This concept is shown in Figs. 8.9(a) and (b) respectively.
Fig. 8.9 ∣ Mp and Mr for x = 0
- As
- Choosing the value of damping ratio
 :
:
The damping ratio
 should be chosen between 0.4 and 0.707 (i.e., 0.4 <
should be chosen between 0.4 and 0.707 (i.e., 0.4 <  < 0.707) to have a tolerable
< 0.707) to have a tolerable  and
and  . If the chosen
. If the chosen  is less than 0.4, both
is less than 0.4, both  have larger values that are not desirable for the system.
have larger values that are not desirable for the system. - Variations of
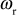 and
and  with respect to
with respect to  :
:
When the value of
 is chosen between 0.4 and 0.707, the value of
is chosen between 0.4 and 0.707, the value of  and
and  are comparable to each other.
are comparable to each other.When
 , both the values of
, both the values of  and
and  approach
approach  .
.When
 is small, then the values of
is small, then the values of 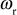 and
and  are:
are:-
 will be large and hence the rise time is small.
will be large and hence the rise time is small. -
 will be large and the response of the system will be faster.
will be large and the response of the system will be faster.
Here, the value of
 indicates the speed of the response. The above concept is shown in Figs. 8.10(a) and (b).
indicates the speed of the response. The above concept is shown in Figs. 8.10(a) and (b).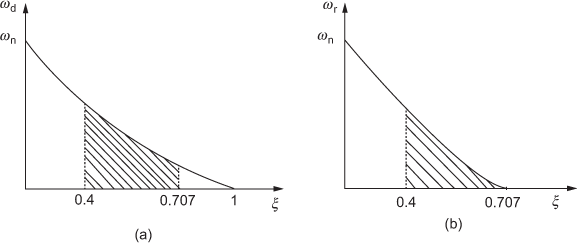
Fig. 8.10 ∣ ωd and ωr for different values of ξ
-
(iii) Bandwidth
The range of frequencies between zero and cut-off frequency ![]() , is known as bandwidth and the cut-off frequency is defined as the frequency at which the magnitude of the system is 3 dB down the magnitude of the system at zero frequency. Hence, bandwidth is nothing but the cut-off frequency
, is known as bandwidth and the cut-off frequency is defined as the frequency at which the magnitude of the system is 3 dB down the magnitude of the system at zero frequency. Hence, bandwidth is nothing but the cut-off frequency ![]() .
.
Assuming the magnitude of the system at zero frequency as 1, the cut-off frequency is derived as
![]() =
= ![]() =
= ![]()
But from Eqn. (8.16), it is clear that the magnitude depends on the normalized frequency. Hence, the above equation can be written as
![]() =
= ![]()

![]()
![]()
![]()
Comparing the above equation with the quadratic equation ![]() , we obtain
, we obtain
![]()
Hence, solving this quadratic equation, we obtain

Considering only the positive values, we obtain ![]()
Therefore, ![]() (8.23)
(8.23)
We know that, ![]()
Therefore, the cut-off frequency is given by ![]() (8.24)
(8.24)
The expression for bandwidth is also same as that of the cut-off frequency. From Eqn. (8.23), the normalized bandwidth ![]() is equal to 1. The graphical idea about the bandwidth with respect to the damping ratio
is equal to 1. The graphical idea about the bandwidth with respect to the damping ratio ![]() is shown in Fig. 8.11.
is shown in Fig. 8.11.

Fig. 8.11 ∣ Magnitude versus frequency
The graphical idea between the normalized bandwidth ![]() and the damping ratio
and the damping ratio ![]() is shown in Fig. 8.12.
is shown in Fig. 8.12.

Fig. 8.12 ∣ ξ vs normalized bandwidth
Example 8.3 The open-loop or the feed-forward transfer function of a unity feedback system is given by ![]() . Determine the resonant frequency and resonant peak for the given system.
. Determine the resonant frequency and resonant peak for the given system.
Solution: Given ![]() and
and ![]() .
.
Hence, the closed-loop transfer function of the system, 
The characteristic equation of the given system is ![]()
Comparing the above equation with the standard second-order characteristic ![]() , we obtain
, we obtain
![]() , i.e.,
, i.e., ![]() rad/sec and
rad/sec and ![]() , i.e.,
, i.e., ![]()
Hence, ![]()
Resonant peak, 
![]()
Resonant frequency, ![]()
![]() rad/sec
rad/sec
Example 8.4 The closed-loop poles of a system are at ![]() . Determine (i) bandwidth, (ii) normalized peak driving signal frequency and (iii) resonant peak for such a system.
. Determine (i) bandwidth, (ii) normalized peak driving signal frequency and (iii) resonant peak for such a system.
Solution: The closed-loop transfer function of any system is given by
and the characteristic equation of the system is given by
![]()
The closed-loop poles of a system are obtained by equating the characteristic equation to zero. Hence, the characteristic equation of the given system using the given closed-loop poles is obtained as ![]()
i.e., ![]()
Comparing the above equation with the standard second-order characteristic equation, we obtain ![]() . Therefore,
. Therefore, ![]() rad/sec
rad/sec
![]()
Therefore, ![]()
Using the damping ratio and natural frequency, the frequency domain specifications can be determined as given below:
- Bandwidth (BW) =

 = 4.350 rad/sec
= 4.350 rad/sec - Normalized peak driving signal frequency (
 ) is
) is
 =
=
 = 0.3846
= 0.3846 - Resonant peak,

Therefore,
 =
=  = 1.083
= 1.083
Example 8.5 Consider a second-order system with a natural frequency of 4 rad/sec and damped natural frequency of 1.6 rad/sec. Determine (i) the percentage of peak overshoot when the system is subjected to a unit step input and (ii) the resonant peak value when the system is subjected to sinusoidal input.
Solution: Given ![]() = 4 rad/sec and
= 4 rad/sec and ![]() = 1.6 rad/sec
= 1.6 rad/sec
We know that ![]()
Therefore, 
Upon solving, we obtain ![]()
- Peak overshoot when subjected to step input =


- Resonance peak,

Example 8.6 Consider a second-order system with resonant peak 2 and resonant frequency of 6 rad/sec. Determine the transfer function of the given second-order system and hence determine (i) rise time tr , (ii) peak time tp , (iii) settling time ts and (iv) % peak overshoot Mp of the given system when the system is subjected to step input. In addition, determine the time of oscillation and number of oscillations before the response of the system gets settled.
Solution: Given ![]() and
and ![]()
We know that 
i.e., 
i.e., 
Upon solving, we obtain ![]()
i.e., ![]() or 0.933
or 0.933
Therefore, ![]() or 0.966
or 0.966
The system with the damping ratio greater than 0.707 does not exhibit any peak in the frequency response of the system. Hence, the damping ratio of the given system is ![]() .
.
We know that, ![]()
Substituting the known values, we obtain ![]()
Upon solving, we obtain ![]() rad/sec
rad/sec
The standard second-order transfer function of the system is 
Substituting the known values, we obtain
 =
= ![]()
Here,  rad
rad
Therefore,  rad
rad
Also, ![]() rad/sec
rad/sec
Rise time, ![]() = 0.2957 sec
= 0.2957 sec
Peak time, ![]() = 0.5045 sec
= 0.5045 sec
Settling time for a system can be determined for 2% error tolerance and 5% error tolerance.
Hence, ![]() sec for 2% tolerance
sec for 2% tolerance
![]() sec for 5% tolerance
sec for 5% tolerance
Period of oscillation, ![]() sec
sec
Number of oscillations before the response of the system gets settled is given by
![]()
Peak overshoot of the system is ![]()
![]() = 0.4309
= 0.4309
Example 8.7 The time response of a second-order system when the system is subjected to a unit step input is given below:

Determine the frequency response parameters of the system (i) peak resonance ![]() , (ii) resonant frequency
, (ii) resonant frequency ![]() and (iii) cut-off frequency of the system
and (iii) cut-off frequency of the system ![]() .
.
Solution:
From the given Table, the maximum value of the time response and the peak time of the system are 1.12 and 0.2 s, respectively.
Hence, there exists a peak overshoot of 0.12 at 0.2 sec.
Therefore, ![]()
Solving the above equation, we obtain ![]()
![]()
i.e., 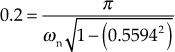
Therefore, ![]() rad/sec
rad/sec

![]() rad/sec
rad/sec

Example 8.8 Consider a unity feedback system as shown in Fig. E8.9. Determine the K and a that satisfies the frequency domain specifications as Mr = 1.04 and ωr = 11.55 rad/sec. In addition, for the determined values of K and a, determine settling time and bandwidth of the system.

Fig. E8.9
Solution: Given ![]() and
and ![]()
Hence, the closed-loop transfer function of the system is

![]()
Comparing the above equation with the standard second-order transfer function, we obtain
![]() i.e.,
i.e., ![]() (1)
(1)
![]() i.e.,
i.e., ![]() (2)
(2)
Using the values of resonant peak and the resonant frequency, the values of K and a can be determined.

i.e.,

Upon solving, we obtain


i.e.,

Upon solving, we obtain
 rad/sec
rad/secSubstituting the values of
 in Eqs. (1) and (2), we obtain
in Eqs. (1) and (2), we obtain
- Settling time,
 sec
sec - Bandwidth,

Example 8.9 The damping ratio and natural frequency of oscillation of a second-order system is 0.5 and 8 rad/sec respectively. Determine the resonant peak and resonant frequency.
Solution: Given ![]() and
and ![]() rad/sec
rad/sec

![]() rad/sec
rad/sec
Example 8.10 The specification given on a certain second-order feedback control system is that the overshoot of the step response should not exceed 25 per cent. What are the corresponding limiting values of the damping ratio ![]() and peak resonance
and peak resonance ![]() ?
?
Solution:
Given ![]()
![]() i.e.,
i.e., ![]()
Therefore, 
i.e., 
or ![]()
i.e., ![]()
Therefore, damping ratio, ![]()
Hence, resonant peak, 
Example 8.11 Determine the frequency specifications of a second-order system when closed transfer function is given by ![]()
Solution: Comparing denominator of the transfer function with ![]() , we obtain
, we obtain
![]() i.e.,
i.e., ![]() and
and ![]() i.e.,
i.e., ![]()

and ![]() rad/sec
rad/sec
![]()
8.8 Effect of Addition of a Pole to the Open-Loop Transfer Function of the System
Consider a system with the open-loop transfer function  . When a pole at
. When a pole at ![]() is added to such a system, the open-loop transfer function of the system becomes
is added to such a system, the open-loop transfer function of the system becomes  . When a sinusoidal input is applied to such a system, the system becomes less stable compared to the stability of the previous system. In addition, the specifications of the frequency domain and time domain vary depending on the time constant
. When a sinusoidal input is applied to such a system, the system becomes less stable compared to the stability of the previous system. In addition, the specifications of the frequency domain and time domain vary depending on the time constant ![]() .
.
For larger values of ![]() , we obtain
, we obtain
- Larger rise time that in turn decreases the bandwidth of the system.
- Larger value of resonant peak that corresponds to a larger value of maximum overshoot in the time response of the system.
8.9 Effect of Addition of a Zero to the Open-Loop Transfer Function of the System
Consider a system with the open-loop transfer function  . When a zero at
. When a zero at ![]() is added, the open-loop transfer function of the system becomes
is added, the open-loop transfer function of the system becomes  . When a sinusoidal input is applied to the system, the following changes occur in the frequency domain specifications.
. When a sinusoidal input is applied to the system, the following changes occur in the frequency domain specifications.
- Bandwidth of the system gets increased.
- Increase in time constant for higher values of Tz.
- Settling time of the system gets increased.
8.10 Graphical Representation of Frequency Response
Determining the frequency response of a system, i.e., the magnitude and phase angle of a system for different frequencies from 0 to ![]() by using tabulation method becomes more complicated when more number of poles and zeros exist in the system. An alternative method that eliminates the difficulty of the tabulation method is the graphical representation of frequency response.
by using tabulation method becomes more complicated when more number of poles and zeros exist in the system. An alternative method that eliminates the difficulty of the tabulation method is the graphical representation of frequency response.
There are different graphical methods by which the frequency response can be represented. They are
- Bode plot (asymptotic plots)
- Polar plot
- Nyquist plot
- Constant M and N circles
- Nichols chart
The Bode plot of representing frequency response of a system is discussed in this chapter and the other plots will be discussed in the subsequent chapters.
8.11 Introduction to Bode Plot
Bode plot introduced by H.W. Bode was first used in the study of feedback amplifiers. It is one of the popular graphical methods used for determining the stability of the system when the system is subjected to sinusoidal input. The stability of the closed-loop system is determined based on the frequency response of the loop transfer function of the system, i.e., ![]() . The gain or magnitude and phase angle of the system can be easily represented as a function of frequency using Bode plot. It is also a very useful graphical tool in analysing and designing of linear control systems.
. The gain or magnitude and phase angle of the system can be easily represented as a function of frequency using Bode plot. It is also a very useful graphical tool in analysing and designing of linear control systems.
The Bode plot consists of two plots:
- Magnitude plot: To plot the logarithmic magnitude or gain of the loop transfer function in dB versus frequency
 i.e.,
i.e.,  .
. - Phase plot: To plot the phase angle of the loop transfer function versus frequency
 i.e.,
i.e.,  .
.
In Bode plot, both the magnitude and phase plots are plotted against the frequency in the logarithmic scale. In addition, the magnitude of the system is plotted in dBs (decibels). Hence, the Bode plot is also called logarithmic plot. Since the magnitude and phase plots of a system are sketched based on the asymptotic properties instead of detailed plotting, the Bode plot is also called asymptotic plots.
8.11.1 Reasons for Using Logarithmic Scale
The reasons for plotting the magnitude and phase angle plots of the Bode plot in a logarithmic scale are:
- In higher order systems, magnitudes of the individual subsystem have to be multiplied to get the magnitude of the higher order system that is a tedious process. But if we use the logarithmic scale, the multiplication part can be replaced by the addition that makes the process of determining the magnitude of the higher order system easier.
- In addition, the variation of frequency in a large scale is easier if we use a logarithmic scale rather than the ordinary scale.
It is noted that in Bode plot, the magnitude of the loop transfer function is taken in terms of decibels (complex logarithm) rather than the simple logarithm. The magnitude used to plot the magnitude plot in Bode plot is determined using
![]() dB
dB
Table 8.3 shows the importance of logarithmic scale rather than the ordinary scale. Any real value existing between ![]() and 100 can be plotted between −40 to 40 dB.
and 100 can be plotted between −40 to 40 dB.
Table 8.3 ∣ The dB values for the original magnitude
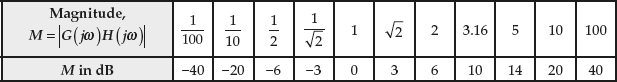
Thus a wide range of magnitude can be plotted easily using logarithmic magnitude scale.
8.11.2 Advantages of Bode Plot
The advantages of using Bode plot in plotting the frequency response of a system are:
- Expansion of frequency range of a system is simple.
- Experimental determination of transfer function of a system is simpler if the frequency response of the system is shown using Bode plot.
- Usage of asymptotic straight lines for approximating the frequency response of the system.
- Bode plot can be plotted for complicated systems.
- Relative stability of the closed-loop system can be analysed by plotting the frequency response of the loop transfer function of the system using Bode plot.
- Frequency domain specifications such as gain crossover frequency, phase crossover frequency, gain margin and phase margin can easily be determined.
- The variation of frequency domain specifications can easily be viewed when a controller is added to the existing system.
- The system gain K can be designed based on the required gain and phase margins.
- Polar plot and Nyquist plot can be constructed based on the data obtained from Bode plot.
8.11.3 Disadvantages of Bode Plot
The disadvantages of using Bode plot in plotting the frequency response of a system are:
- Using Bode plot, it is possible only to determine the absolute and relative stability of the minimum phase system.
- Corrections are to be made in the obtained plot to meet the desired frequency plot.
8.12 Determination of Frequency Domain Specifications from Bode Plot
The different frequency domain specifications that can easily be determined using Bode plot are gain margin, phase margin, gain crossover frequency and phase crossover frequency. The plot shown in Fig. 8.13 indicates the determination of the above said frequency domain specifications.

Fig. 8.13 ∣ Frequency domain specifications
From the above plot, the formula for determining the frequency domain specifications can be obtained as follows:
Gain crossover frequency, ![]() = frequency at which
= frequency at which ![]() = 0.
= 0.
Phase crossover frequency, ![]() = frequency at which
= frequency at which ![]() = −180°.
= −180°.
Gain margin, ![]() = 0 dB −
= 0 dB −![]() .
.
Phase margin, ![]() =
= ![]() − (−180°) = 180°+ phase angle at
− (−180°) = 180°+ phase angle at ![]() .
.
8.13 Stability of the System
The stability of the system is easier to determine using Bode plot once the frequency domain specifications are obtained. The stability of the system can be analysed on the basis of crossover frequencies (![]() and
and ![]() ) or gain and phase margins.
) or gain and phase margins.
8.13.1 Based on Crossover Frequencies
The system can either be a stable system, marginally stable system or unstable system. The stability of the system based on the relation between crossover frequencies is given in Table 8.4.
Table 8.4 ∣ Stability of the system based on crossover frequencies

8.13.2 Based on Gain Margin and Phase Margin
The stability of the system based on the gain margin and phase margin is given in Table 8.5.
Table 8.5 ∣ Stability of the system based on gm and pm

8.14 Construction of Bode Plot
The construction of Bode plot can be illustrated by considering the generalized form of loop transfer function is given by:

where ![]() are real constants,
are real constants,
Z is the number of zeros at the origin,
N is the number of poles at the origin or the TYPE of the system,
M is the number of simple poles existing in the system,
U is the number of simple zeros existing in the system,
V is the number of complex poles existing in the system
Q is the number of complex zeros existing in the system and
T is the time delay in seconds.
Substituting ![]() and simplifying, we obtain
and simplifying, we obtain

Rearranging the above equation, we obtain
 (8.25)
(8.25)
where  ,
, ![]() and
and ![]()
The magnitude of Eqn. (8.25) in dB is given by


The phase angle of Eqn. (8.25) is given by

where magnitude of the term ![]() is 1 and phase angle of the term
is 1 and phase angle of the term ![]() is
is ![]() .
.
It is noted that phase angle of the term ![]() = 0°.
= 0°.
From Eqn. (8.25), it is clear that the open-loop transfer function ![]() may contain the combination of any of the following five factors:
may contain the combination of any of the following five factors:
- Constant K.
- Zeros at the origin
 and poles at the origin
and poles at the origin 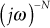 .
. - Simple zero
 and simple pole
and simple pole  .
. - Complex zero
 and complex pole
and complex pole  .
. - Transportation lag
 .
.
Hence, it is necessary to have a complete study (magnitude and phase plots) of these factors that can be utilized in constructing the plot (magnitude and phase plots) of a composite loop transfer function
 . The composite plot for the loop transfer function
. The composite plot for the loop transfer function  is constructed by adding the plots of individual factors present in the function. Thus Bode plot is an approximate asymptotic plot of individual factors.
is constructed by adding the plots of individual factors present in the function. Thus Bode plot is an approximate asymptotic plot of individual factors.
Factor 1: Constant K
The magnitude and phase angle of the constant K which are to be plotted in a semi log graph sheet are:
Magnitude in dB = ![]() .
.
Phase angle = 0°.
The magnitude and phase plots corresponding to the values obtained using the above equation are shown in Figs. 8.14(a) and (b) respectively.

Fig. 8.14 ∣ Bode plot for factor K
Note:
- The constant K can have a value that is either greater than 1 or less than 1. The magnitude corresponding to the gain that is greater than 1 is positive and gain that is less than 1 is negative.
- If the gain K is varied, the corresponding changes occur only in the magnitude plot (i.e., either the plot raises or lowers). If the gain value is increased by a factor 10, then the corresponding magnitude plot gets raised by 20 dB. Similarly, if the gain value is decreased by a factor 10, then the corresponding magnitude plot gets decreased by 20 dB. The proof of this concept is given below.

Similarly,

- In addition, if the magnitude of a constant K is expressed in dB, the magnitude of reciprocal of the particular constant K in dB will have the same value but the sign differs.
i.e.,

Factor 2: Zeros at the origin ![]() or poles at the origin
or poles at the origin ![]()
In Bode plots, the frequency ratios are expressed in terms of octaves or decades. When the frequency band is from ![]() to
to ![]() , it is called decade.
, it is called decade.
The details for plotting the magnitude and phase plots when only one pole or zero exists at the origin are given in Table 8.6.
Table 8.6 ∣ Magnitude and phase plots for ![]() and
and ![]()

The magnitude in dB will be equal to zero at the frequency value of ![]() .
.
If multiple poles or zeros exist at the origin, the corresponding changes in the magnitude and phase plots are given in Table 8.7. Let the number of zeros at the origin existing in the system be Z and the number of poles at the origin be N.
Table 8.7 ∣ Magnitude and phase plots for ![]() and
and ![]()

Factor 3: Simple pole ![]() or simple zero
or simple zero ![]()
The details for plotting the magnitude and phase plots when only one simple pole or simple zero exists are given in Table 8.8.
Table 8.8 ∣ Magnitude and phase angle for simple pole and simple zero

It is known that the magnitude of a number is same as the magnitude of the reciprocal of a number with the opposite sign. Hence, in this case the step-by-step procedure for plotting the magnitude and phase plots for a simple pole are discussed.
For simple pole ![]()
Magnitude plot
- The magnitude of the simple pole in dB is
 .
. - Consider two cases:
Case 1: For low frequencies

Magnitude =

Slope =

Case 2: For high frequencies

Magnitude =

The slope of the line is determined as follows:
At
 , magnitude = 0 dB
, magnitude = 0 dBAt
 , magnitude = −20 dB
, magnitude = −20 dBHence, the slope of the line is

- Hence, the magnitude plot of the simple pole can be approximated using the two straight-line asymptotes
- Straight line at 0 dB
 .
. - Straight line with the slope of

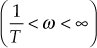
The approximate magnitude plot of the simple pole is shown in Fig. 8.15(a).

Fig. 8.15 (a) ∣ Approximate magnitude plot for

- Straight line at 0 dB
Corner frequency
The frequency at which two asymptotes meet is called corner frequency or break frequency. In this case, the corner frequency is at ![]() . The corner frequency divides the frequency response curve of the system as low-frequency region and high-frequency region.
. The corner frequency divides the frequency response curve of the system as low-frequency region and high-frequency region.
Error in the magnitude plot
The magnitude plot obtained using the above three steps is an approximated magnitude curve. The actual magnitude curve can be obtained by substituting different values of ![]() in magnitude equation of simple pole as given in Table 8.9.
in magnitude equation of simple pole as given in Table 8.9.
Table 8.9 ∣ Actual magnitude curve

Hence, an error exists in the magnitude plot. The error in the magnitude plot is maximum at the corner frequency and the value of the error is obtained by
Error = 
The values of error at different frequencies are given in Table 8.10.
Table 8.10 ∣ Error versus Frequency ![]()

The magnitude plot with the approximate curve and actual curve is shown in Fig. 8.15(b).

Fig. 8.15 (b) ∣ Magnitude plot for (1 + jωT)−1
Phase plot
- The phase angle for a simple pole is
 .
. - The phase plot for a simple pole is obtained by substituting different values of
 .
.
At
 , phase angle = 0°
, phase angle = 0°At
 , phase angle = −45°
, phase angle = −45°At
 , phase angle = −90°
, phase angle = −90°Hence, the phase plot of a simple pole is shown in Fig. 8.15(c).

Fig. 8.15 (c) ∣ Approximate phase plot for (1 + jωT)−1
The phase plot of a simple pole is skew symmetric about the inflection point at phase angle = −45°.
Some errors exist in the phase plot when the actual value is approximated and the approximate phase angle value and actual phase angle at different frequencies are given in Table 8.11.
Table 8.11 ∣ Exact and approximate phase values for simple zero

The phase plot with the approximate curve and actual curve are shown in Fig. 8.15(d).

Fig. 8.15 (d) ∣ Phase plot for a simple pole
For simple zero 
The reciprocal of a simple pole is a simple zero. Hence, the magnitude and phase plots of a simple zero are just the mirror image of the plots of simple pole. The magnitude and phase plots of a simple zero with the actual curve and approximated curve are shown in Figs. 8.15(e) and (f) respectively.


Fig. 8.15 ∣ Bode plot for simple zero (1 + jωT)−1
If the number of simple poles and simple zeros of same value existing on the system is ![]() , then the magnitude and phase plots are obtained as
, then the magnitude and phase plots are obtained as
- Corner frequency is the same i.e.,
 .
. - Low-frequency asymptote is a horizontal straight line at
 .
. - High-frequency asymptote is a straight line with the slope of


- The phase angle in the phase plot of the system is
 times the phase angle of the simple pole or simple zero at each frequency.
times the phase angle of the simple pole or simple zero at each frequency. - Error in each plot is
 times the error of simple pole or simple zero.
times the error of simple pole or simple zero.
Factor 4: Complex zero  and complex pole
and complex pole 
The details for plotting the magnitude and phase plots of complex pole and complex zero is given in Table 8.12.
Table 8.12 ∣ Magnitude and phase angle for complex zero and complex pole

In Table 8.12, ![]() is the damping ratio and
is the damping ratio and ![]() .
.
It is known that the magnitude of a number is same as the magnitude of the reciprocal of that number with opposite sign. The magnitude and phase plots of the quadratic factor depend on the corner frequency and the damping factor. Hence, in this case, the step-by-step procedure for plotting the magnitude and phase plots for simple poles has been discussed.
8.14.1 Effect of Damping Ratio 
When the damping ratio is greater than 1, i.e., ![]() , the quadratic factor can be written as the product of two first-order factors with real poles. When the damping ratio is within a range, i.e.,
, the quadratic factor can be written as the product of two first-order factors with real poles. When the damping ratio is within a range, i.e., ![]() , the quadratic factor can be written as the product of two complex conjugate factors. The asymptotic approximation of the plots is not accurate for this factor with lower values of
, the quadratic factor can be written as the product of two complex conjugate factors. The asymptotic approximation of the plots is not accurate for this factor with lower values of ![]() .
.
Complex pole 
The step-by-step procedure for plotting the magnitude and phase plots for a complex pole is discussed below.
Magnitude plot:
- The magnitude of the simple pole in dB is
 (8.26)
(8.26) - Consider two cases:
Case 1: For lower frequencies
 ,
,Magnitude =

Slope =

Case 2: For higher frequencies
 ,
,Magnitude =

The slope of the line is determined as
At
 , magnitude = 0 dB
, magnitude = 0 dBAt
 , magnitude = −40 dB
, magnitude = −40 dBHence, the slope of the line is
 .
. - Hence, the magnitude plot of the simple pole can be approximated using the two straight-line asymptotes
- Straight line at 0 dB
 .
. - Straight line with the slope of

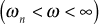 .
.
- Straight line at 0 dB
The approximate magnitude plot of the complex pole is shown in Fig. 8.16(a).

Fig. 8.16 (a) ∣ Approximate magnitude plot for ![]()
At the corner frequency i.e., ![]() , the resonant peak occurs and its magnitude depends on
, the resonant peak occurs and its magnitude depends on ![]() . Also, error exists in the approximation of two asymptotes and the magnitude of the error depends inversely on damping ratio
. Also, error exists in the approximation of two asymptotes and the magnitude of the error depends inversely on damping ratio ![]() .
.
The actual magnitude curve can be obtained by substituting different values of ![]() in Eqn. (8.26) as given in Table 8.13.
in Eqn. (8.26) as given in Table 8.13.
Table 8.13 ∣ Actual magnitude curve

Hence, error always exists in the magnitude plot of the system. The error at ![]() is calculated as given below:
is calculated as given below:
Error = actual value − approximate value
=![]() dB
dB
The error for different values of ![]() at
at ![]() is given in Table 8.14. Similarly, error will vary depending on
is given in Table 8.14. Similarly, error will vary depending on ![]() and
and ![]() .
.
Table 8.14 ∣ Error versus damping ratio at ![]()

The magnitude plot with the actual and asymptotic value is shown in Fig. 8.16(b).

Fig. 8.16 (b) ∣ Magnitude plot for ![]()
Phase plot
- The phase angle for the simple pole is given by
-
 for
for 
-
 for
for 
-
- The phase plot for the simple pole is obtained by substituting different values of
 .
.
At
 , phase angle = 0°
, phase angle = 0°At
 , phase angle = −90°
, phase angle = −90°At
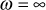 , phase angle = −180°
, phase angle = −180°
Hence, the phase plot of a complex pole is shown in Fig. 8.16(c).

Fig. 8.16 (c) ∣ Phase plot for ![]()
The phase plot of a simple pole is skew symmetric about the inflection point at phase angle = −90°.
Complex zero 
Plots for a quadratic zero are mirror images of those for a pole. The magnitude and phase plots for a complex zero are shown in Figs. 8.16(d) and (e) respectively.


Fig. 8.16 ∣ Bode plot for complex zero ![]()
It is noted that in the quadratic zero when the damping ratio is less than 0.7 (i.e., ![]() ), a dip has to be drawn at frequency
), a dip has to be drawn at frequency ![]() with the amplitude of
with the amplitude of ![]() .
.
Similarly, for quadratic pole when the damping ratio is less than 0.7 (i.e., ![]() ), a peak has to be drawn at frequency
), a peak has to be drawn at frequency ![]() with the amplitude of
with the amplitude of ![]() .
.
Factor 5: Transportation lag, ![]()
Consider a system with loop transfer function as
![]()
In frequency domain, the loop transfer function is given by
![]()
where T is the time delay in seconds.
Therefore, ![]()
Hence, the magnitude and phase angle of the factor is given by
![]()
and 
Since the phase angle obtained is in the unit of radians, the phase angle can be calculated in degrees as
![]()
Table 8.15 shows the phase angle for different values of ![]() .
.
Table 8.15 ∣ Phase angle versus frequency ![]()

It is clear that for the transportation lag factor, the magnitude plot is zero for all the values of frequency ![]() and the phase plot is varying linearly with the frequency
and the phase plot is varying linearly with the frequency ![]() .
.
Table 8.16 shows the different factors with its corner frequency, slope of the magnitude curve, values of the magnitude in dB and phase angle in degrees.
Table 8.16 ∣ Possible factors present in a given system

8.15 Constructing the Bode Plot for a Given System
Consider the loop transfer function as

Substituting ![]() , we obtain
, we obtain

Now, the corner frequencies of the given system are
![]()
The phase plot is independent of the corner frequency. Since the magnitude of each term present in the transfer function is calculated in the increasing order of corner frequency, the magnitude plot depends on the corner frequency.
Hence, the relation between the corner frequencies is considered as ![]() .
.
8.15.1 Construction of Magnitude Plot
For each term present in the loop transfer function, the slope of the magnitude curve varies. To combine the slope of the different terms present in the given system, the following steps are followed:
- Slope of each term is calculated.
- Change in slope from one term to another in the order of increasing corner frequencies has to be determined using Table 8.17. Usually, the constant term along with the pole or zero at the origin is taken as a term.
Table 8.17 ∣ Determination of change in slope at different corner frequencies

- Two different frequencies other than the corner frequencies are chosen arbitrarily as lower frequency value
 and higher frequency value
and higher frequency value  such that the relation between different frequencies is
such that the relation between different frequencies is

- Determine the gain at different frequencies in increasing order. In this case, there are five different frequencies and have only four terms. Hence, the magnitude of the first term in Table 8.17 is calculated at the first two frequencies. In this case, the magnitude of
 is calculated at
is calculated at  and
and  . The calculation of magnitude at other frequencies
. The calculation of magnitude at other frequencies  and
and  is done using the formula
is done using the formula
Gain at

where

The gain at different frequencies are tabulated as given in Table 8.18.
Table 8.18 ∣ Gain at different frequencies

- Any term in the estimation of magnitude has to be included only after its corresponding corner frequency is crossed.
- Using Table 8.18, the magnitude plot for the given system can be drawn.
8.15.2 Construction of Phase Plot
The construction of phase plot is much simpler when compared to construction of magnitude plot.
The phase angle of the given system as a function of frequency ![]() has to be determined as
has to be determined as
 for
for ![]()
and 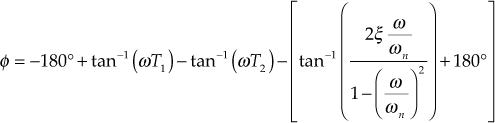 for
for ![]()
The values of ![]() at different frequencies are calculated including the frequencies mentioned in Table 8.18 and tabulated.
at different frequencies are calculated including the frequencies mentioned in Table 8.18 and tabulated.
8.16 Flow Chart for Plotting Bode Plot
The flow chart for plotting the Bode plot (both magnitude and phase angle plot) for a given system is shown in Fig. 8.17.

Fig. 8.17 ∣ Flow chart for plotting the Bode plot for a system
8.17 Procedure for Determining the Gain K from the Desired Frequency Domain Specifications
The flow chart for determining the gain K for the desired ![]() is given in Fig. 8.18(a).
is given in Fig. 8.18(a).

Fig. 8.18 (a) ∣ Determination of K for the desired ωgc
The flow chart for determining the gain K for the desired ![]() is given in Fig. 8.18(b).
is given in Fig. 8.18(b).

Fig. 8.18 (b) ∣ Determination of K for the desired gm
The flow chart for determining the gain ![]() for the desired
for the desired ![]() is shown in Fig. 8.18(c).
is shown in Fig. 8.18(c).

Fig. 8.18 (c) ∣ Determination of K for the desired pm
8.18 Maximum Value of Gain
The gain ![]() has an effect only on the magnitude plot of a loop transfer function of a system. The magnitude plot of a loop transfer function can be shifted vertically upwards or vertically downwards depending on the gain
has an effect only on the magnitude plot of a loop transfer function of a system. The magnitude plot of a loop transfer function can be shifted vertically upwards or vertically downwards depending on the gain ![]() . If there is an increase in gain value from the original value, then the magnitude plot gets shifted vertically upward and if there is a decrease in gain from the original value, then the magnitude plot gets shifted vertically downward. The gain value cannot be increased or decreased infinitely. There exists some limits in doing so. The gain can be increased or decreased till the magnitude reaches
. If there is an increase in gain value from the original value, then the magnitude plot gets shifted vertically upward and if there is a decrease in gain from the original value, then the magnitude plot gets shifted vertically downward. The gain value cannot be increased or decreased infinitely. There exists some limits in doing so. The gain can be increased or decreased till the magnitude reaches ![]() dB at phase crossover frequency. The new gain can be determined as
dB at phase crossover frequency. The new gain can be determined as
![]()
where ![]() is the value by which the magnitude plot has been raised or lowered to reach
is the value by which the magnitude plot has been raised or lowered to reach ![]() dB at
dB at ![]() .
.
8.19 Procedure for Determining Transfer Function from Bode Plot
The step-by-step procedure for determining the transfer function of a system from its magnitude plot are:
Step 1: Determine the number of corner frequencies existing in the system (the point at which the slope of the system changes). If there exist ![]() different slopes for the given system, then there exist
different slopes for the given system, then there exist ![]() different corner frequencies.
different corner frequencies.
Step 2: Determine the initial slope and final slope of the system.
Step 3: Construct a table for the given system in the format given below to determine the different factors present in the system.

Step 4:Determine the gain ![]() , corner frequencies, unknown frequencies and unknown magnitude values using the equation of a straight line,
, corner frequencies, unknown frequencies and unknown magnitude values using the equation of a straight line, ![]() , where
, where ![]() is the magnitude in dB,
is the magnitude in dB, ![]() is the slope of the line in dB/dec,
is the slope of the line in dB/dec, ![]() is the logarithmic value of frequency
is the logarithmic value of frequency ![]() , i.e.,
, i.e., ![]() in rad/sec and
in rad/sec and ![]() is the constant.
is the constant.
8.20 Bode Plot for Minimum and Non-Minimum Phase Systems
Consider the loop transfer function of a minimum phase transfer function as
![]() (8.27)
(8.27)
and the loop transfer function of a non-minimum phase system as
![]() (8.28)
(8.28)
where ![]()
The pole-zero plots of the minimum and non-minimum systems are shown in Fig. 8.19.

Fig. 8.19 ∣ Pole-zero plots of (a) minimum and (b) non-minimum phase systems
The magnitude and phase angle of the transfer function can be obtained by substituting ![]() in Eqs. (8.27) and (8.28) as
in Eqs. (8.27) and (8.28) as
 and
and  (8.29)
(8.29)
 (8.30)
(8.30)
From Eqs. (8.29) and (8.30), it is clear that the magnitudes of minimum phase system and non-minimum phase system are same, whereas the phase angles of minimum phase system and non-minimum phase system are different. The magnitude and phase plots of minimum and non-minimum phase systems are shown in Fig. 8.20.

Fig. 8.20 ∣ Phase plot of minimum and non-minimum phase systems
Example 8.12 The loop transfer function of a system is given by ![]() . Sketch the Bode plot and determine the following frequency domain specifications (i) gain margin
. Sketch the Bode plot and determine the following frequency domain specifications (i) gain margin ![]() , (ii) phase margin
, (ii) phase margin ![]() , (iii) gain crossover frequency
, (iii) gain crossover frequency ![]() and (iv) phase crossover frequency
and (iv) phase crossover frequency ![]() . Also, comment on the stability of the system.
. Also, comment on the stability of the system.
Solution:
- The loop transfer function of a system is given by

- Substituting
 , we obtain
, we obtain

- Two corner frequencies exist in the given loop transfer function are:
 rad/sec and
rad/sec and  rad/sec.
rad/sec.To sketch the magnitude plot
- The change in slope at different corner frequencies are given in Table E8.12(a).
Table E8.12(a) ∣ Determination of change in slope at different corner frequencies

- Assume the lower frequency as
 = 1 rad/sec and higher frequency as
= 1 rad/sec and higher frequency as  = 30 rad/sec.
= 30 rad/sec. - The values of gain at different frequencies are determined and given in Table E8.12(b).
Table E8.12(b) ∣ Gain at different frequencies

- The magnitude plot of the given system is plotted using Table E8.12(b) and is shown in Fig. E8.12(a).
To sketch the phase plot
- The phase angle of the given loop transfer function as a function of frequency is obtained as

- The phase angle at different frequencies are obtained by using the above equation and the values are tabulated as given in Table E8.12(c).
Table E8.12(c) ∣ Phase angle of the system for different frequencies

- The phase plot of the given system is plotted using Table E8.12(c) and is shown in Fig. E8.12(b).
Hence, the magnitude and phase plots for the loop transfer function of the system are shown in Fig. E8.12.

Fig. E8.12
- The frequency domain specifications for the given system can be obtained by drawing two horizontal lines across the two plots of the given system (one across the magnitude plot at 0 dB and another across the phase plot at −180°).
From the definition of gain crossover frequency, phase crossover frequency, gain margin, phase margin and from the graph shown in Fig. E8.12, the frequency domain specifications values are obtained as
Gain crossover frequency,
 rad/sec
rad/secPhase crossover frequency,
 rad/sec
rad/secGain margin,
 dB
dBPhase margin,
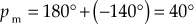
- The stability of the system can be determined based on either the frequency or the gain.
Based on frequency:
Since
 , the system is stable.
, the system is stable.Based on frequency domain specifications:
Since the gain margin and phase margin are greater than zero and
 , the system is stable.
, the system is stable.
Example 8.13 The loop transfer of a given system is given by ![]() . Sketch the Bode plot for given system. In addition, (i) determine the gain K and the phase margin so that gain margin is +30 dB and (ii) determine the gain K and the gain margin so that phase margin is
. Sketch the Bode plot for given system. In addition, (i) determine the gain K and the phase margin so that gain margin is +30 dB and (ii) determine the gain K and the gain margin so that phase margin is ![]() .
.
Solution:
- Given
 .
. - Substituting
 and
and  , we obtain
, we obtain

- The two corner frequencies in the given system are
 rad/sec and
rad/sec and  rad/sec.
rad/sec.To sketch the magnitude plot
- The change in slope at different corner frequencies is given in Table E8.13(a).
Table E8.13(a) ∣ Determination of change in slope at different corner frequencies

- Assume the lower frequency as
 = 0.1 rad/sec and higher frequency as
= 0.1 rad/sec and higher frequency as  = 20 rad/sec.
= 20 rad/sec. - The values of gain at different frequencies are determined and given in Table E8.13(b).
Table E8.13(b) ∣ Gain at different frequencies

- The magnitude plot of the given system is plotted using Table E8.13(b) and is shown in Fig. E8.13(a).
To sketch the phase plot
- The phase angle of the given loop transfer function as a function of frequency is obtained as
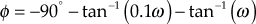
- The phase angles at different frequencies are tabulated as given in Table E8.13(c).
Table E8.13(c) ∣ Phase angle of the system for different frequencies

- The phase plot of the given system is plotted using Table E8.13(c) and is shown in Fig. E8.13(a).

Fig. E8.13 (a)
- The frequency domain specifications for the given system can be obtained by drawing two horizontal lines across the two plots of the given system (one across the magnitude plot at 0 dB and the other across the phase plot at −180°).
From the definitions of gain crossover frequency, phase crossover frequency, gain margin, phase margin and the graph shown in Fig. E8.13(a), the frequency domain specifications values are obtained as
Gain crossover frequency,
 rad/sec
rad/secPhase crossover frequency,
 rad/sec
rad/secGain margin,
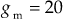 dB
dBPhase margin,

- The next step is to determine the gain
 corresponding to a particular gain margin and phase margin.
corresponding to a particular gain margin and phase margin.
(i) To determine the gain value ![]() and gain margin corresponding to desired phase margin:
and gain margin corresponding to desired phase margin:
The required phase margin for the system is ![]() .
.
But it is known that, phase margin ![]() .
.
Therefore, ![]() .
.
Hence, from Fig. E8.13(a), the new gain crossover frequency for a phase angle of ![]() is
is ![]() rad/sec.
rad/sec.
It is proven that at the gain crossover frequency, the magnitude must be 0 dB. But from Fig. E8.13(a), the magnitude at ![]() dB. Hence, the magnitude plot shown in Fig. E8.13(a) is raised by 5dB.
dB. Hence, the magnitude plot shown in Fig. E8.13(a) is raised by 5dB.
The modified Bode plot is shown in Fig. E8.13(b).
From Fig. E8.13(b), the new frequency domain specifications are
New phase margin, ![]()
New gain margin, ![]() =16 dB
=16 dB
New gain crossover frequency, ![]() 1.3 rad/sec
1.3 rad/sec
The value of ![]() for the newly obtained Bode plot is determined as
for the newly obtained Bode plot is determined as
![]() where
where ![]() is the value in dB by which the original magnitude plot has been raised or lowered. In this case, the value of
is the value in dB by which the original magnitude plot has been raised or lowered. In this case, the value of ![]() is 5 dB.
is 5 dB.
Hence, ![]()
![]()
Therefore, the value of ![]() is
is ![]() .
.

Fig. E8.13 (b)
(ii) To determine the gain ![]() and phase margin corresponding to the gain margin
and phase margin corresponding to the gain margin
The required gain margin ![]() dB.
dB.
We know that, the gain margin is obtained using the formula,
![]()
Therefore, required ![]() is
is ![]() dB.
dB.
But for the given system from the Bode plot shown in Fig. E8.13(a), the gain at ![]() is
is ![]() dB. Hence, it is clear that every point in the magnitude plot shown in Fig. E8.13(a), has to be reduced by
dB. Hence, it is clear that every point in the magnitude plot shown in Fig. E8.13(a), has to be reduced by ![]() dB. The modified Bode plot is shown in Fig. E8.13(c).
dB. The modified Bode plot is shown in Fig. E8.13(c).
From the Bode plot shown in Fig. E8.13(c), the obtained frequency domain specifications are:
New phase margin, ![]()
New gain margin, ![]() = 30 dB
= 30 dB
The value of ![]() for the newly obtained Bode plot is determined as
for the newly obtained Bode plot is determined as
![]() , where
, where ![]() is the value in dB by which the original magnitude plot has been raised or lowered. In this case, the value of
is the value in dB by which the original magnitude plot has been raised or lowered. In this case, the value of ![]() is −10.
is −10.
Hence, ![]()
![]()
Therefore, the value of ![]() is
is ![]() .
.

Fig. E8.13 (c)
Example 8.14 The loop transfer function of a system is given by  . Sketch the Bode plot for the given system. Also, determine the gain value K for the gain crossover frequency 5 rad/sec.
. Sketch the Bode plot for the given system. Also, determine the gain value K for the gain crossover frequency 5 rad/sec.
Solution:
- The loop transfer function of the system is given by
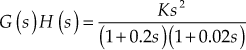 .
. - Substituting
 and
and  in the given system, we obtain
in the given system, we obtain

- The two corner frequencies existing in the system are
 rad/sec and
rad/sec and  rad/sec.
rad/sec. - The change in slope at different corner frequencies is given in Table E8.14(a).
Table E8.14(a) ∣ Determination of change in slope at different corner frequencies

- Assume
 rad/sec and
rad/sec and 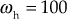 rad/sec.
rad/sec. - The values of gain at different frequencies are determined and given in Table E8.14(b).
Table E8.14(b) ∣ Gain at different frequencies

- The magnitude plot of the given system is plotted using Table E8.14(b) and is shown in Fig. E8.14(a).
To sketch the phase plot
- The phase angle of the given loop transfer function as a function of frequency is obtained as

- The phase angles at different frequencies are tabulated as given in Table E8.14(c).
Table E8.14(c) ∣ Phase angle of the system for different frequencies

- The phase plot of the given system is plotted using Table E8.14(c) and is shown in Fig. E8.14(a).

Fig. E8.14 (a)
- The frequency domain specifications for the given system are:
Gain crossover frequency, (ωgc) = 1 rad/sec.
Phase crossover frequency, ( ωpc) = 0 rad/sec.
Gain margin, (gm) = ∞ dB.
Phase margin, (pm) = −50°.
- The next step is to determine the gain
 corresponding to a particular gain crossover frequency.
corresponding to a particular gain crossover frequency.
It is given that the required gain crossover frequency of the system is ![]() rad/sec, i.e.,
rad/sec, i.e., ![]() rad/sec. Hence, it is necessary that the magnitude of the system at
rad/sec. Hence, it is necessary that the magnitude of the system at ![]() must be 0 dB. But from the Bode plot of the system shown in Fig. E8.14(a), the magnitude of the system is 28 dB.
must be 0 dB. But from the Bode plot of the system shown in Fig. E8.14(a), the magnitude of the system is 28 dB.
Therefore, each and every point present in the magnitude plot must be added by ![]() dB. Hence, the modified Bode plot with
dB. Hence, the modified Bode plot with ![]() rad/sec is shown in Fig. E8.14(b).
rad/sec is shown in Fig. E8.14(b).

Fig. E8.14 (b)
The value of ![]() for the new Bode plot is determined as follows:
for the new Bode plot is determined as follows:
![]() where
where ![]() is the value by which the magnitude plot has been raised or lowered. In this case,
is the value by which the magnitude plot has been raised or lowered. In this case, ![]() dB.
dB.
Hence, ![]()
![]()
Therefore, the ![]() =
= ![]() .
.
Example 8.15 The loop transfer function of the system is given by  . Sketch the Bode plot for the system. Also, determine the frequency domain specifications and hence determine the stability of the system.
. Sketch the Bode plot for the system. Also, determine the frequency domain specifications and hence determine the stability of the system.
Solution:
- The loop transfer function of the system is
 .
. - Substituting
 , we obtain
, we obtain

- The three corner frequencies existing in the system are
 rad/sec,
rad/sec,  rad/sec and
rad/sec and  rad/sec.
rad/sec.To sketch the magnitude plot
- The change in slope at different corner frequencies is given in Table E8.15(a).
Table E8.15(a) ∣ Determination of change in slope at different corner frequencies

- Assume
 rad/sec and
rad/sec and  rad/sec.
rad/sec. - The values of gain at different frequencies are determined and given in Table E8.15(b).
Table E8.15(b) ∣ Gain at different frequencies

- The magnitude plot of the given system is plotted using Table E8.15(b) and is shown in Fig. E8.15.
To sketch the phase plot
- The phase angle of the given loop transfer function as a function of frequency is obtained as

- The phase angles at different frequencies are tabulated as given in Table E8.15(c).
Table E8.15(c) ∣ Phase angle of the system for different frequencies
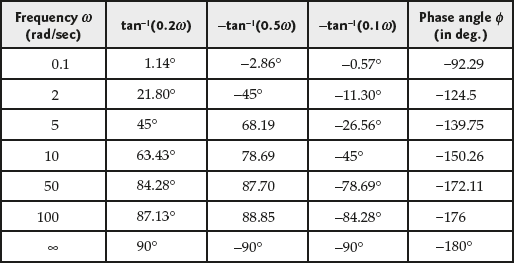
- The phase plot of the given system is plotted using Table E8.15(c) and is shown in Fig. E8.15.

Fig. E8.15
- The frequency domain specifications for the given system are:
Gain crossover frequency,
 rad/sec
rad/secPhase margin,

From Table E8.15(c), it is clear that the phase angle of the system becomes
 only when the frequency of the system is ∞ rad/sec. Hence, phase crossover frequency of the system is ∞ rad/sec. Therefore, the gain margin of the system is also ∞ dB.
only when the frequency of the system is ∞ rad/sec. Hence, phase crossover frequency of the system is ∞ rad/sec. Therefore, the gain margin of the system is also ∞ dB. - The stability of the system can be determined based on either the frequency or the gain.
Based on frequency: Since
 , the system is stable.
, the system is stable.Based on frequency domain specifications: Since the gain margin and phase margin are greater than zero and
 , the system is stable.
, the system is stable.
Example 8.16 The loop transfer function of a system is given by  . Sketch the Bode plot for the given system and determine the frequency domain specifications.
. Sketch the Bode plot for the given system and determine the frequency domain specifications.
Solution:
- The loop transfer function of the given system is
 .
. - Substituting
 and rearranging, we obtain
and rearranging, we obtain

- The three corner frequencies existing in the system are
 rad/sec,
rad/sec,  rad/sec and the third corner frequency is obtained as follows.
rad/sec and the third corner frequency is obtained as follows.Comparing the standard second-order characteristic equation with the given quadratic factor, we obtain
 rad/sec and
rad/sec and 
Hence, the third corner frequency existing in the system is
 rad/sec.
rad/sec.To sketch the magnitude plot
- The change in slope at different corner frequencies are given in Table E8.16(a).
Table E8.16(a) ∣ Determination of change in slope at different corner frequencies

- Assume
 rad/sec and
rad/sec and  rad/sec.
rad/sec. - The values of gain at different frequencies are determined and given in Table E8.16(b).
Table E8.16(b) ∣ Gain at different frequencies
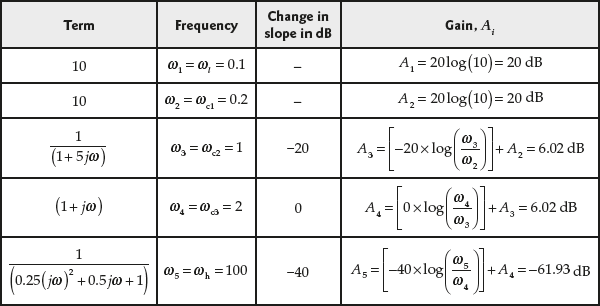
- The magnitude plot of the given system is plotted using Table E8.16(b) and is shown in Fig. E8.16.
To sketch the phase plot
- The phase angle of the given loop transfer function as a function of frequency is obtained as

- The phase angles at different frequencies are tabulated as given in Table E8.16(c).
Table E8.16(c) ∣ Phase angle of the system for different frequencies

- The phase plot of the given system is plotted using Table E8.16(c) and is shown in Fig. E8.16.

Fig. E8.16
- The frequency domain specifications are:
Gain crossover frequency,
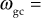 2.8 rad/sec
2.8 rad/secPhase crossover frequency,
 rad/sec
rad/secGain margin,
 dB
dBPhase margin,

Example 8.17 The loop transfer function of a system is given by  . Sketch the Bode plot for the given system and determine the frequency domain specifications.
. Sketch the Bode plot for the given system and determine the frequency domain specifications.
Solution:
- The loop transfer function of the given system is

- Substituting
 and rearranging, we obtain
and rearranging, we obtain

- The two corner frequencies existing in the system are
 rad/sec and
rad/sec and  rad/sec.
rad/sec.To sketch the magnitude plot
- The change in slope at different corner frequencies is given in Table E8.17(a).
Table E8.17(a) ∣ Determination of change in slope at different corner frequencies

- Assume
 rad/sec and
rad/sec and  rad/sec.
rad/sec. - The values of gain at different frequencies are determined and given in Table E8.17(b).
Table E8.17(b) ∣ Gain at different frequencies

- The magnitude plot of the given system is plotted using Table E8.17(b) and is shown in Fig. E8.17.
To sketch the phase plot
- The phase angle of the given loop transfer function as a function of frequency is obtained as
 .
. - The phase angles at different frequencies are tabulated as given in Table E8.17(c).
Table E8.17(c) ∣ Phase angle of the system for different frequencies

- The phase plot of the given system is plotted using Table E8.17(c) and is shown in Fig. E8.17.

Fig. E8.17
- The frequency domain specifications of the system are:
Gain crossover frequency,
 rad/sec
rad/secPhase crossover frequency,
 rad/sec
rad/secGain margin,
 dB
dBPhase margin,

Example 8.18 The loop transfer function of a given system is ![]() . Sketch the Bode plot for the given system.
. Sketch the Bode plot for the given system.
Solution:
- The loop transfer function of the given system is
 .
. - Substituting
 , we obtain
, we obtain 
- It is known that for a simple zero, the slope is
 dB/dec and there exists no corner frequency for the given system. Hence, for the given system the slope is
dB/dec and there exists no corner frequency for the given system. Hence, for the given system the slope is  .
. - As there exists only one factor in the given system, the change in slope cannot be determined.
- The magnitude for the given system is

- The phase angle for the given system is

Hence, the magnitude and phase plots for the given system depends on ![]() .
.
Example 8.19 The frequency response of a unity feedback system is given in Table E8.19.
Table E8.19 ∣ Frequency response of a system

Determine (a) gain margin and phase margin of the system and (b) change in gain so that the gain margin of the system is ![]() dB.
dB.
Solution:
- From Table E8.19, the frequency domain specifications are:
Gain crossover frequency,
 rad/sec
rad/secPhase crossover frequency,
 rad/sec
rad/secGain margin,
 dB
dBPhase margin,

- For the gain
 , the gain margin
, the gain margin  dB. But the required gain margin is
dB. But the required gain margin is  dB. Therefore, the magnitude at different frequency should increase by
dB. Therefore, the magnitude at different frequency should increase by  dB.
dB.
Hence,

i.e.,
 .
.Therefore, change in gain required to have the gain margin of the system as
 dB is
dB is  .
.
Example 8.20 The loop transfer function of a system is given by  . Sketch the Bode plot for the given system and determine the frequency domain specifications.
. Sketch the Bode plot for the given system and determine the frequency domain specifications.
Solution:
- The loop transfer function of the given system is

- Rearranging the above equation, we obtain

- The three corner frequencies existing in the system are
 rad/sec,
rad/sec, 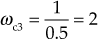 rad/sec and the third corner frequency is obtained as follows.
rad/sec and the third corner frequency is obtained as follows.
Comparing the standard second-order characteristic equation with the given quadratic factor, we obtain
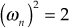 rad/sec and
rad/sec and 
Hence, the third corner frequency existing in the system is
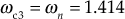 rad/sec.
rad/sec.To sketch the magnitude plot
- The change in slope at different corner frequencies is given in Table E8.20(a).
Table E8.20(a) ∣ Determination of change in slope at different corner frequencies

- Assume
 rad/sec and
rad/sec and  rad/sec.
rad/sec. - The values of gain at different frequencies are determined and given in Table E8.20(b).
Table E8.20(b) ∣ Gain at different frequencies

- The magnitude plot of the given system is plotted using Table E8.20(b) and is shown in Fig. E8.20.
To sketch the phase plot
- The phase angle of the given loop transfer function as a function of frequency is obtained as

- The phase angles at different frequencies are tabulated as given in Table E8.20(c).
Table E8.20(c) ∣ Phase angle of the system for different frequencies

- The phase plot of the given system is plotted using Table E8.20(c) and is shown in Fig. E8.20.
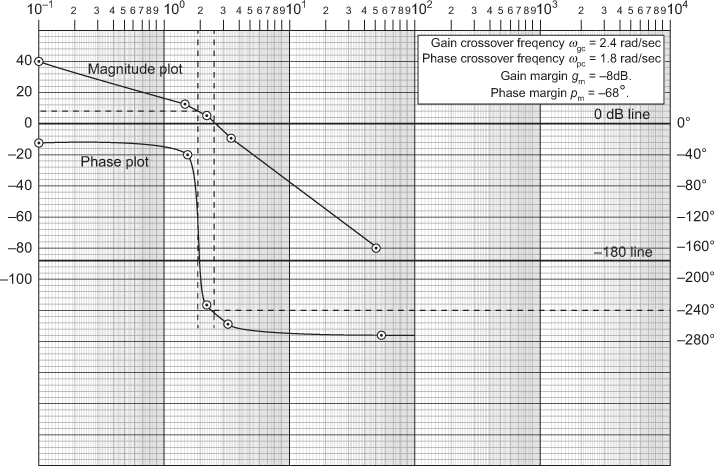
Fig. E8.20
- The frequency domain specifications for the system are:
Gain crossover frequency,
 rad/sec
rad/secPhase crossover frequency,
 rad/sec
rad/secGain margin,
 dB
dBPhase margin,

Example 8.21 The loop transfer function of a system is given by ![]() . Sketch the Bode plot for the given system and determine the frequency domain specifications.
. Sketch the Bode plot for the given system and determine the frequency domain specifications.
Solution:
- The loop transfer function of the given system is

- Substituting
 , we obtain
, we obtain

- The corner frequency that exists in the system is
 rad/sec
rad/sec
To sketch the magnitude plot
- The change in slope at different corner frequencies is given in Table E8.21(a).
Table E8.21(a) ∣ Determination of change in slope at different corner frequencies
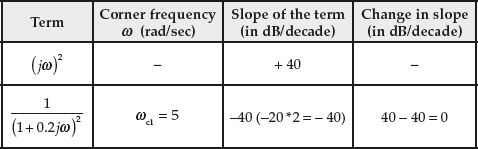
- Assume
 rad/sec and
rad/sec and  rad/sec.
rad/sec. - The values of gain at different frequencies are determined and given in Table E8.21(b).
Table E8.21(b) ∣ Gain at different frequencies

- The magnitude plot of the given system is plotted using Table E8.21(b) and is shown in Fig. E8.21.
To sketch the phase plot
- The phase angle of the given loop transfer function as a function of frequency is obtained as
 =
= 
- The phase angle at different frequencies are tabulated as given in Table E8.21(c).
Table E8.21(c) ∣ Phase angle of the system for different frequencies

- The phase plot of the given system is plotted using Table E8.21(c) and is shown in Fig. E8.21.

Fig. E8.21
- The frequency domain specifications of the system are:
Gain crossover frequency,
 rad/sec
rad/secPhase crossover frequency,
 rad/sec
rad/secGain margin,
 dB
dBPhase margin,

Example 8.22 The loop transfer function of a system is given by  . Sketch the Bode plot for the given system. Determine the frequency domain specifications.
. Sketch the Bode plot for the given system. Determine the frequency domain specifications.
Solution:
- The loop transfer function of the given system is

- As the roots of the quadratic factor are real, we can split the quadratic factor as

- Substitute
 and rearranging, we obtain
and rearranging, we obtain

=

- The four corner frequencies existing in the system are
 rad/sec,
rad/sec,  rad/sec,
rad/sec,  rad/sec and
rad/sec and rad/sec.
rad/sec.To sketch the magnitude plot
- The change in slope at different corner frequencies is given in Table E8.22(a).
- Assume
 rad/sec and
rad/sec and  rad/sec.
rad/sec.
Table E8.22(a) ∣ Determination of change in slope at different corner frequencies

- The values of gain at different frequencies are determined and given in Table E8.22(b).
Table E8.22(b) ∣ Gain at different frequencies

- The magnitude plot of the given system is plotted using Table E8.22(b) and is shown in Fig. E8.22.
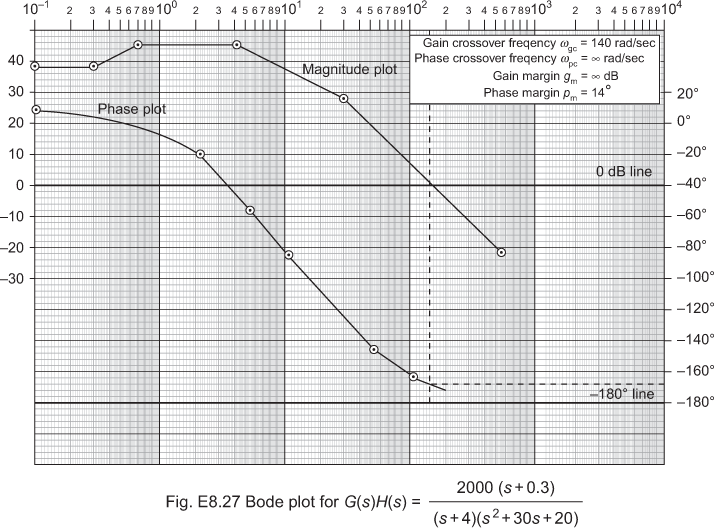
Fig. E8.22
To sketch the phase plot
- The phase angle of the given loop transfer function as a function of frequency is obtained as

- The phase angles at different frequencies are tabulated as given in Table E8.22(c).
Table E8.22(c) ∣ Phase angle of the system for different frequencies

- The phase plot of the given system is plotted using Table E8.22(c) and is shown in Fig. E8.22.
- The frequency domain specifications of the given system are:
Gain crossover frequency,
 rad/sec
rad/secPhase crossover frequency,
 rad/sec
rad/secGain margin,
 dB
dBPhase margin,

Example 8.23 The loop transfer function of a system is given by ![]() . Sketch the Bode plot for the given system and determine the frequency domain specifications.
. Sketch the Bode plot for the given system and determine the frequency domain specifications.
Solution:
- The loop transfer function of the given system is

- Substituting
 and
and  and rearranging, we obtain
and rearranging, we obtain

where
 .
. - The two corner frequencies existing in the system are
 rad/sec and
rad/sec and  rad/sec.
rad/sec.To sketch the magnitude plot
- The change in slope at different corner frequencies is given in Table E8.23(a).
Table E8.23(a) ∣ Determination of change in slope at different corner frequencies

- Assume
 rad/sec and
rad/sec and  rad/sec.
rad/sec. - The values of gain at different frequencies are determined and given in Table E8.23(b).
Table E8.23(b) ∣ Gain at different frequencies

- It is known that the delay term (
 ) present in the loop transfer function will contribute only to phase angle plot. Hence, the magnitude plot of any system with or without delay terms is same.
) present in the loop transfer function will contribute only to phase angle plot. Hence, the magnitude plot of any system with or without delay terms is same. - The magnitude plot of the given system is plotted using Table E8.23(b) and is shown in Fig. E8.23.
To sketch the phase plot
- The phase angle of the given loop transfer function as a function of frequency is obtained as


=

- The phase angles at different frequencies are tabulated as given in Table E8.23(c).
Table E8.23(c) ∣ Phase angle of the system for different frequencies

- The phase plot of the given system is plotted using Table E8.23(c) and is shown in Fig. E8.23.

Fig. E8.23
- The frequency domain specifications of the system are:
Gain crossover frequency,
 rad/sec
rad/secPhase crossover frequency,
 rad/sec
rad/secGain margin,
 dB
dBPhase margin,

Example 8.24 The block diagram of a system with ![]() and
and ![]() is shown in Fig. E8.24(a). Determine the loop transfer function and sketch the Bode plot for the same. Also, determine the maximum gain
is shown in Fig. E8.24(a). Determine the loop transfer function and sketch the Bode plot for the same. Also, determine the maximum gain ![]() before the system becomes unstable.
before the system becomes unstable.

Fig. E8.24(a)
Solution:
- The loop transfer function of the system shown in Fig. E8.24(a) is
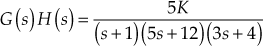 .
. - Substituting
 and
and  and rearranging, we obtain
and rearranging, we obtain

- The three corner frequencies existing in the system are
 rad/sec,
rad/sec,  rad/sec and
rad/sec and  rad/sec.
rad/sec.To sketch the magnitude plot
- The change in slope at different corner frequencies is given in Table E8.24(a).
Table E8.24(a) ∣ Determination of change in slope at different corner frequencies

- Assume
 rad/sec and
rad/sec and  rad/sec.
rad/sec. - The values of gain at different frequencies are determined and given in Table E8.24(b).
Table E8.24(b) ∣ Gain at different frequencies

- The magnitude plot of the given system is plotted using Table E8.24(b) and is shown in Fig. E8.24(b).

Fig. E8.24(b)
To sketch the phase plot
- The phase angle of the given loop transfer function as a function of frequency is obtained as

- The phase angles at different frequencies are tabulated as given in Table E8.24(c).
Table E8.24(c) ∣ Phase angle of the system for different frequencies

- The phase plot of the given system is plotted using Table E8.24(c) and is shown in Fig. E8.24(b).
- The frequency domain specifications of the system are:
Gain crossover frequency,
 rad/sec
rad/secPhase crossover frequency,
 rad/sec
rad/secGain margin,
 dB
dBPhase margin,

To determine the maximum gain

- The magnitude in dB at
 is 37 dB. Therefore, the magnitude plot can be raised by dB until the magnitude becomes
is 37 dB. Therefore, the magnitude plot can be raised by dB until the magnitude becomes  dB at
dB at  . Therefore, the maximum gain
. Therefore, the maximum gain  is determined as
is determined as


Example 8.25 The loop transfer function of a system is given by  . Determine the maximum value of time delay
. Determine the maximum value of time delay ![]() , for the closed-loop system to be stable.
, for the closed-loop system to be stable.
Solution:
- The loop transfer function of the given system is

- Substituting
 , we obtain
, we obtain
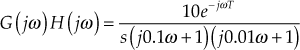
- The two corner frequencies existing in the system are
 rad/sec and
rad/sec and  .
.To sketch the magnitude plot
- The change in slope at different corner frequencies is given in Table E8.25(a).
Table E8.25(a) ∣ Determination of change in slope at different corner frequencies

- Assume
 rad/sec and
rad/sec and  rad/sec.
rad/sec. - The values of gain at different frequencies are determined and given in Table E8.25(b).
Table E8.25(b) ∣ Gain at different frequencies

- It is known that the delay term (
 ) present in the loop transfer function will contribute only to the phase angle plot. Hence, the magnitude plot of any system with or without delay term is same.
) present in the loop transfer function will contribute only to the phase angle plot. Hence, the magnitude plot of any system with or without delay term is same. - It is clear from Table E8.25(b) that the gain crossover frequency
 is
is  rad/sec.
rad/sec. - The phase angle of the system is
 (1)
(1) - To determine the maximum value of time delay,
 :
:
The phase margin for the system to be stable is
 . Therefore,
. Therefore,
Substituting Eqn. (1) in the above equation, we obtain
![]()
Substituting ![]() = 10 rad/sec, we obtain
= 10 rad/sec, we obtain
![]()
![]() i.e., T = 0.068 sec.
i.e., T = 0.068 sec.
Therefore, maximum time delay, ![]() , for the closed-loop system to be stable is
, for the closed-loop system to be stable is ![]() sec.
sec.
Example 8.26 The magnitude plot of a system is shown in Fig. E8.26(a). Determine the transfer function of the system.

Fig. E8.26 (a)
Solution:
From Fig. E8.26(a), we can obtain the following information:
- Three corner frequencies exist in the system
- Initial slope of the plot =
 dB/decade
dB/decade - Final slope of the plot =
 dB/decade
dB/decade
The change in slope from initial to final slope occurs in three steps and the factor that could be present in the transfer function for that change in slope to occur is given in Table E8.26.
Table E8.26 ∣ Factor for the change in slope

Therefore, from the above table, we can determine the loop transfer function of the system as a function of gain value ![]() as
as
![]()
The values of time constants ![]() and
and ![]() can be determined from their respective corner frequencies as
can be determined from their respective corner frequencies as
![]() ,
, ![]() and
and ![]() .
.
Hence, the loop transfer function of the system as a function of ![]() is
is
![]()
To determine the gain K
The gain ![]() can be determined using the general equation of straight line, i.e.,
can be determined using the general equation of straight line, i.e., ![]() where
where ![]() is the magnitude of
is the magnitude of ![]() in dB,
in dB, ![]() is the slope of the line,
is the slope of the line, ![]() is the logarithmic frequency in
is the logarithmic frequency in ![]() and
and ![]() is the constant.
is the constant.
The given magnitude plot of a system is redrawn as shown in Fig. E8.26(b).

Fig. E8.26(b)
For the line segment ![]() , we have
, we have
Slope of the line, ![]() .
.
Therefore, ![]()
At ![]()
![]() dB.
dB.
Therefore, ![]() i.e., c =32.
i.e., c =32.
The magnitude at ![]() is
is ![]()
Solving the above equation, we obtain ![]() dB.
dB.
At ![]() rad/sec, only the gain and poles at the origin exist in the system, i.e.,
rad/sec, only the gain and poles at the origin exist in the system, i.e., ![]() .
.
Therefore, ![]()
![]()
![]()
Therefore, ![]() .
.
Hence, the transfer function for the given magnitude plot of a system is
![]()
Example 8.27 The magnitude plot of a particular system is shown in Fig. E8.27(a). Determine the transfer function of the system.

Fig. E8.27 (a)
Solution:
From Fig. E8.27(a), we can obtain the following information:
- Three corner frequencies exist in the system
- Initial slope of the plot = 0 dB/decade
- Final slope of the plot =
 dB/decade
dB/decade
The change in slope from initial to final slope occurs in three steps and the factor that could be present in the transfer function for that change in slope to occur is given in Table E8.27.
Table E8.27 ∣ Factor for the change in slope

Therefore, from Table E8.27, we can determine the loop transfer function of the system as a function of gain value ![]() as
as

To determine the gain K and corner frequencies:
- As the initial slope of the magnitude plot is
 dB/decade and the magnitude is
dB/decade and the magnitude is  dB, we obtain the gain
dB, we obtain the gain  as
as

Therefore,

- Corner frequencies
The gain
 can be determined using the general equation of straight line, i.e.,
can be determined using the general equation of straight line, i.e.,  where
where  is the magnitude of
is the magnitude of  in dB,
in dB,  is the slope of the line,
is the slope of the line,  is the logarithmic frequency in
is the logarithmic frequency in  and
and  is the constant.
is the constant.The magnitude plot given in Fig. E8.27(a) can be redrawn as shown in Fig. E8.27(b).

Fig. E8.27 (b)
For the line segment ![]() , we have
, we have ![]()
Therefore, ![]()
At ![]() ,
, ![]() dB.
dB.
Therefore, ![]()
Solving the above equation, we obtain ![]()
Also, at ![]() ,
, ![]() dB
dB
Therefore, ![]()
Solving the above equation, we obtain ![]() s.
s.
Similarly, for line segment ![]() , we have
, we have ![]()
Therefore, ![]()
At ![]() ,
, ![]() dB.
dB.
Therefore, ![]()
Solving the above equation, we obtain ![]()
Also, at ![]() ,
, ![]() dB
dB
Therefore, ![]()
Solving the above equation, we obtain ![]() s.
s.
Similarly, for line segment ![]() , we have
, we have
![]()
Therefore, ![]()
At ![]() ,
, ![]() dB.
dB.
Therefore, ![]()
Solving the above equation, we obtain ![]()
Also, at ![]() ,
, ![]() dB
dB
Therefore, ![]()
Solving the above equation, we obtain ![]() s.
s.
Therefore, the required transfer function will be

Review Questions
- Define frequency response of a system and discuss about the advantages of frequency response method for the analysis of linear systems.
- Discuss the correlation between frequency response and transient response for a second-order system. Derive any expression used.
- Explain the procedure to get the closed-loop frequency response from the loop transfer function.
- Explain the procedure for experimentally determining the frequency response of an electric circuit containing several interconnected components. Draw a complete schematic diagram of the experimental set-up.
- What are the different methods available for frequency response plot?
- Discuss the advantages of frequency response analysis over the root locus technique.
- Write down the frequency domain specifications.
- Define the frequency domain specification for bandwidth.
- What are the advantages and disadvantages of having large bandwidth?
- Express the resonant peak Mp and the resonant frequency
 in terms of natural frequency of oscillation
in terms of natural frequency of oscillation  and damping ratio
and damping ratio  for a unity feedback second-order system.
for a unity feedback second-order system. - If a control system is required to have a given value for the resonant peak, describe how you would get the required value of the static loop gain
 , given the loop transfer function.
, given the loop transfer function. - Explain the effect of feedback on the gain and bandwidth of the system.
- What do you understand by frequency response plot?
- What are the unique features of Bode plots?
- What is corner frequency in Bode plot?
- Define minimum phase transfer function.
- Explain the gain margin and phase margin.
- Define gain and phase crossover frequencies.
- Explain the significance of phase margin and gain margin in determining the relative stability of closed-loop systems.
- What are the advantages and disadvantages of Bode plot?
- What is the major difference between Bode magnitude plots for first-order system and second-order system?
- Describe the change in open-loop frequency response magnitude plot if the time delay is added to the plant.
- If the phase response of a pure time delay is plotted on a linear phase versus linear frequency plot, what would be the shape of the curve?
- What will be initial slope of the Bode magnitude plot for a system having no poles and no zeros at origin?
- Tabulate the phase angle versus frequency for the loop transfer function of a system given by
 .
. - A second-order system has a natural frequency of oscillation
 rad/sec and damped frequency of oscillation
rad/sec and damped frequency of oscillation  rad/sec. Determine (i) when it is subjected to a step input, calculate its percentage overshoot and (ii) when it is subjected to a sinusoidal input, calculate the maximum ratio to its output (resonant peak).
rad/sec. Determine (i) when it is subjected to a step input, calculate its percentage overshoot and (ii) when it is subjected to a sinusoidal input, calculate the maximum ratio to its output (resonant peak). - An under damped second-order system exhibited 17% overshoot for a step input, and the frequency of oscillations was 0.5 Hz. Calculate the resonant peak Mp and the resonant frequency
 of the frequency response of this system.
of the frequency response of this system. - A closed-loop transfer function of an automatic control system is given by

Calculate (i) the peak response
 and resonant frequency
and resonant frequency  of the system and (ii) damping ratio and natural frequency of oscillation
of the system and (ii) damping ratio and natural frequency of oscillation  of the equivalent second-order system.
of the equivalent second-order system. - The overshoot of the unit step response of a second-order feedback system is 30 per cent. Determine (a) damping ratio
 , (b) resonant peak
, (b) resonant peak  , (c) resonant frequency
, (c) resonant frequency  , (d) damping frequency
, (d) damping frequency  and (e) time at which peak overshoot occurs. Assume natural frequency of oscillation
and (e) time at which peak overshoot occurs. Assume natural frequency of oscillation  rad/sec.
rad/sec. - Determine the bandwidth for the closed-loop transfer function given by

- The transfer function of a system is given by
 . Show that
. Show that  .
. - The closed-loop transfer function of a unity feedback control system is
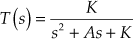 . The peak overshoot for a unit step input is 25 per cent. The damped frequency of oscillation is
. The peak overshoot for a unit step input is 25 per cent. The damped frequency of oscillation is  rad/sec. Determine
rad/sec. Determine  , bandwidth and the time at which the first overshoot occurs. In addition, find the steady state error of the system if
, bandwidth and the time at which the first overshoot occurs. In addition, find the steady state error of the system if  .
. - For
 if
if  and
and  rad/sec, determine
rad/sec, determine  and
and  and hence calculate the settling time and bandwidth.
and hence calculate the settling time and bandwidth. - A control system is represented by Fig. Q8.34.

Fig. Q8.34
Determine (i) the values of
 and
and  so that
so that  and
and  rad/sec and (ii) corresponding bandwidth.
rad/sec and (ii) corresponding bandwidth. - The transfer function of a system is given by
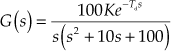 . (a) When
. (a) When  , determine the maximum time delay
, determine the maximum time delay  in seconds for the closed-loop system to be stable and (b) when
in seconds for the closed-loop system to be stable and (b) when  sec determine the maximum gain
sec determine the maximum gain  for the system to be stable.
for the system to be stable. - For a unity feedback system shown in Fig. Q8.36, determine (a)
 , (b)
, (b)  and (c) bandwidth of the system for
and (c) bandwidth of the system for  and
and  .
.

Fig. Q8.36
- Consider a unity feedback system whose loop transfer function is
 . Determine gain
. Determine gain  such that the resonant peak magnitude in the frequency response is 2 dB or
such that the resonant peak magnitude in the frequency response is 2 dB or  dB.
dB. - A unit step input is applied to a feedback control system whose open-loop transfer function is given by
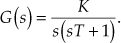 Determine
Determine  and
and  given that maximum overshoot is 26 per cent and resonant frequency is
given that maximum overshoot is 26 per cent and resonant frequency is  rad/sec. Calculate resonance peak
rad/sec. Calculate resonance peak  , gain crossover frequency and phase margin.
, gain crossover frequency and phase margin. - For each closed-loop system with the following performance characteristics, determine the closed-loop bandwidth for (a)
 , (b)
, (b)  , (c)
, (c)  and (d)
and (d)  .
. - Determine the resonant frequency
 , resonant peak
, resonant peak  and bandwidth for the system whose transfer function is given by
and bandwidth for the system whose transfer function is given by  .
. - Determine the phase crossover frequency, gain crossover frequency, gain margin and phase margin for the given system with
 and
and  without plotting the Bode plot. Also comment on the stability of the stability.
without plotting the Bode plot. Also comment on the stability of the stability. - Determine analytically the gain margin and phase margin for the system with the following transfer function
 . Also determine the gain crossover frequency and phase cross over frequency.
. Also determine the gain crossover frequency and phase cross over frequency. - The transfer function of an electric circuit is
 . Determine (a) gain margin and phase margin and (b) gain and phase angle at a frequency of 1 kHz.
. Determine (a) gain margin and phase margin and (b) gain and phase angle at a frequency of 1 kHz. - An amplifier is subjected to a sinusoidal voltage gain as
 . Determine the amplitude of output signal and the phase difference between output and input. The amplifier transfer function is
. Determine the amplitude of output signal and the phase difference between output and input. The amplifier transfer function is  .
. - A sinusoidal waveform
 is fed to a constant block with a transfer function of 0.675. Determine (a) signal gain, (b) output amplitude and (c) phase difference between input and output.
is fed to a constant block with a transfer function of 0.675. Determine (a) signal gain, (b) output amplitude and (c) phase difference between input and output. - The loop transfer function of a system is given by
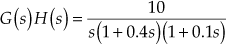 . Sketch the Bode plot for the given system. Also, determine the frequency domain specifications.
. Sketch the Bode plot for the given system. Also, determine the frequency domain specifications. - The loop transfer function of a system is given by
 . Sketch the Bode plot for the given system and determine the frequency domain specifications.
. Sketch the Bode plot for the given system and determine the frequency domain specifications. - The loop transfer function of a system is given by
 . Sketch the Bode plot for the given system and determine the frequency domain specifications.
. Sketch the Bode plot for the given system and determine the frequency domain specifications. - The loop transfer function of a system is given by
 . Sketch the Bode plot for the given system and determine the frequency domain specifications.
. Sketch the Bode plot for the given system and determine the frequency domain specifications. - The loop transfer function of a system is given by
 . Sketch the Bode plot for the given system and determine the frequency domain specifications.
. Sketch the Bode plot for the given system and determine the frequency domain specifications. - The loop transfer function of a system is given by
 . Sketch the Bode plot for the given system and determine the frequency domain specifications.
. Sketch the Bode plot for the given system and determine the frequency domain specifications. - The loop transfer function of a system is given by
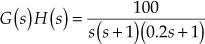 . Sketch the Bode plot for the given system and determine the frequency domain specifications.
. Sketch the Bode plot for the given system and determine the frequency domain specifications. - The loop transfer function of a system is given by
 . Sketch the Bode plot for the given system and determine the frequency domain specifications.
. Sketch the Bode plot for the given system and determine the frequency domain specifications. - The loop transfer function of a system is given by
 . Sketch the Bode plot for the given system and determine the frequency domain specifications.
. Sketch the Bode plot for the given system and determine the frequency domain specifications. - The loop transfer function of a system is given by
 . Sketch the Bode plot for the given system and determine the frequency domain specifications.
. Sketch the Bode plot for the given system and determine the frequency domain specifications. - Determine the gain and phase margins of the system using Table Q8.56.
Table Q8.56

- The loop transfer function of a system is
 . Determine the gain margin and phase margin using Bode plot.
. Determine the gain margin and phase margin using Bode plot. - A constant block has a magnitude of 20 dB at 100 rad/sec. Determine (a) block transfer function, (b) magnitude at a frequency of 1,000 rad/sec and (c) phase angle at 1,000 rad/sec.
- Determine the stability of the system using Bode plot whose block diagram is given in Fig. Q8.59.

Fig. Q8.59
- A unity feedback control system is characterized by an open-loop transfer function
 .
.Show that the gain margin of the system is

- A negative feedback control system is characterized by an open-loop transfer function
 . Determine (a)
. Determine (a)  for a gain margin
for a gain margin  of 10 dB, (b)
of 10 dB, (b)  for a
for a  of 30 dB, (c) K to give phase margin
of 30 dB, (c) K to give phase margin  of 24° and (d) the marginal value of
of 24° and (d) the marginal value of  for stability.
for stability. - At the phase crossover frequency, the gain of the system is
 . What is the corresponding gain margin in dB?
. What is the corresponding gain margin in dB? - The block diagram of a floppy disc is shown in Fig. Q8.64.
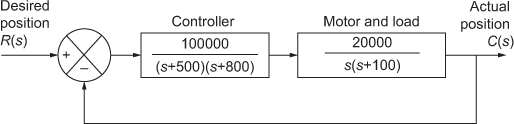
Fig. Q8.64
Use frequency response technique to determine (a)
 , zero dB frequency 180° frequency, (b) closed-loop bandwidth, percentage overshoot, settling time and peak time and also comment on the stability of the system.
, zero dB frequency 180° frequency, (b) closed-loop bandwidth, percentage overshoot, settling time and peak time and also comment on the stability of the system. - Draw the Bode plot for the transfer function

- The open-loop transfer function of a unity feedback system is given by
 .
.Derive an expression for gain K in terms of
 and specified gain margin
and specified gain margin  .
. - For the given transfer function
 sketch the Bode magnitude and phase angle plot. Obtain gain margin and phase margin.
sketch the Bode magnitude and phase angle plot. Obtain gain margin and phase margin. - The loop transfer function of a system is given by
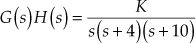 . Sketch the Bode plot for the given system. Also, determine the gain K when the gain margin is 10 dB.
. Sketch the Bode plot for the given system. Also, determine the gain K when the gain margin is 10 dB. - The loop transfer function of a system is given by
 . Sketch the Bode plot for the given system. Also, determine the gain K when the phase margin is 30°.
. Sketch the Bode plot for the given system. Also, determine the gain K when the phase margin is 30°. - The loop transfer of a given system is given by
 . Sketch the Bode plot for the given system. Also, determine the gain margin and phase margin of the system.
. Sketch the Bode plot for the given system. Also, determine the gain margin and phase margin of the system. - The loop transfer function of a system is given by
 . Sketch the Bode plot for the given system and determine the frequency domain specifications.
. Sketch the Bode plot for the given system and determine the frequency domain specifications. - A servo control system of type 0, has a transfer function
 . Sketch the Bode plot and comment on the stability of the system.
. Sketch the Bode plot and comment on the stability of the system. - Explain the Bode plot for the following functions of a unity feedback system.
(i)
 (ii)
(ii)  and (iii)
and (iii) 
- Explain the Bode plot for the following functions of a unity feedback system:
(i)
 and (ii)
and (ii) 
- The closed-loop control system incorporating an amplifier with a gain of K is shown in Fig. Q8.75.

Fig. Q8.75
Using Bode plot, determine (a) is the system stable for a gain K = 1 and (b) what is the maximum value of K before the system becomes unstable.
- Draw the Bode plot for the system shown in Fig. Q8.76. Determine (i)
 and
and  (ii) whether the closed-loop system is stable (iii) obtain the closed-loop frequency response and plot on a Bode diagram. Find the resonance frequency and bandwidth. What are the values of
(ii) whether the closed-loop system is stable (iii) obtain the closed-loop frequency response and plot on a Bode diagram. Find the resonance frequency and bandwidth. What are the values of  and settling time?
and settling time?

Fig. Q8.76
- Sketch the Bode plot for the loop transfer function
 . Determine the maximum value of
. Determine the maximum value of  for the system to be stable.
for the system to be stable. - Draw the Bode plot for the transfer function
 where
where  .
. - For the following transfer function, identify the corner frequencies, the initial slope and the final slope of the magnitude plot

- Consider a system as shown in Fig. Q8.80.

Fig. Q8.80
Determine (a) phase margin for the time delay of 0, 0.1, 0.2, 0.5 and 1 s (b) gain margin for the time delay mentioned in (a), (c), for what time delay mentioned in (a), the system is stable and (d) for each time delay that makes the system unstable, how much reduction in gain is required for the system to be stable?
- The open-loop transfer function of a unity feedback system is
 . Using Bode plot, determine (a)
. Using Bode plot, determine (a)  so that the
so that the  is 20 dB, (b)
is 20 dB, (b)  so that the
so that the  is 60° and (c)
is 60° and (c)  so that the resonant peak
so that the resonant peak  of the system is 1 dB. What are the corresponding values of
of the system is 1 dB. What are the corresponding values of  and
and  and (d)
and (d)  so that the bandwidth
so that the bandwidth  of the system is 1.5 rad/sec.
of the system is 1.5 rad/sec. - Describe the asymptotic phase response of a system with a single pole at −2.
- For a system with three poles at −4, what is the maximum difference between the asymptotic approximation and the actual magnitude response?
- The loop transfer function of a system is given by
 . Sketch the Bode plot for the following two cases: (i)
. Sketch the Bode plot for the following two cases: (i)  and (ii)
and (ii) .
. - Consider a system as shown in Fig. Q8.85. Determine the loop transfer function and sketch the Bode diagram for the same. Also, determine the value of gain
 such that the phase margin is
such that the phase margin is 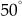 . What is the gain margin of this system with this gain
. What is the gain margin of this system with this gain  ?
?

Fig. Q8.85
- The block diagram of a control system is shown in Fig. Q8.86. Determine the range of the gain
 for stability.
for stability.

Fig. Q8.86
- Determine the gain margin, phase margin, damping factor and critical frequency of oscillation for the system with unity feedback and has a transfer function
 .
. - Sketch the Bode plot for the loop transfer function of the system
 .
.Determine the range of K for closed-loop stability.
- Determine the gain and phase angle of the system at a frequency of 1 rad/sec. The transfer function of the system is G(s) = (s + 1).
- The transfer function of the system is given by
 . Determine the frequency response of the system over a frequency range of 0.1₧10 rad/sec.
. Determine the frequency response of the system over a frequency range of 0.1₧10 rad/sec. - Determine the gain and phase angle of the given system at a frequency of 0.1 Hz. The transfer function of the system is
 .
.
