9.1 Introduction to Polar Plot
The presence of magnitude plot and phase plot for showing the variation of gain and phase angle of a system with respect to the change in frequency is the major disadvantage of the Bode plot. The plot that combines both the plots to a single plot without losing any information is called polar plot. The polar plot can be plotted either on a polar graph or on an ordinary graph. Hence, polar plot for a particular system can be defined in two ways based on the graph used for plotting. The two different definitions for polar plot are given below:
The polar plot of a loop transfer function ![]() is defined as a plot of
is defined as a plot of ![]() versus
versus ![]() on the polar coordinates as the frequency
on the polar coordinates as the frequency ![]() varies from zero to infinity when it is plotted on a polar graph. Also, it is defined as a plot of real part of
varies from zero to infinity when it is plotted on a polar graph. Also, it is defined as a plot of real part of ![]() versus imaginary part of
versus imaginary part of ![]() as the frequency
as the frequency ![]() varies from zero to infinity when it is plotted on an ordinary graph. The real and imaginary parts of the transfer function
varies from zero to infinity when it is plotted on an ordinary graph. The real and imaginary parts of the transfer function ![]() can be denoted as
can be denoted as ![]() and
and ![]() respectively.
respectively.
The concentric circles present in the polar graph represent the magnitude of the transfer function and the radial lines crossing the circles represent the phase angle of the transfer function. The phase angle of the transfer function ![]() can either be positive or negative. Hence, it can be noted that on a polar graph, positive phase angle is measured in counterclockwise direction and negative phase angle is measured in clockwise direction. A simple example of polar plot of a transfer function on an ordinary graph and on a polar graph is shown in Figs. 9.1(a) and (b) respectively.
can either be positive or negative. Hence, it can be noted that on a polar graph, positive phase angle is measured in counterclockwise direction and negative phase angle is measured in clockwise direction. A simple example of polar plot of a transfer function on an ordinary graph and on a polar graph is shown in Figs. 9.1(a) and (b) respectively.

Fig. 9.1 ∣ Polar plot on a graph
9.2 Starting and Ending of Polar Plot
The polar plot of any system starts from one quadrant on an ordinary graph and ends at the other quadrant. The starting and ending point of the polar plot depends on the type and order of the loop transfer function.
The starting point of the polar plot depends on the type of the loop transfer function of a given system as shown in Fig. 9.2(a). If the type of the loop transfer function of a given system ![]() is greater than 3, then the starting point of such system follows the system with type
is greater than 3, then the starting point of such system follows the system with type ![]() .
.

Fig. 9.2 ∣ Starting and ending points of polar plot
The ending point of the polar plot depends on the order of the loop transfer function as shown in Fig. 9.2(b). Similar to the starting point of the polar plot, if the order of the loop transfer function of the given system m > 4, then the ending point of such system follows the system with order ![]() .
.
It can be noted that this method of determining the starting and ending points of the polar plot is applicable to the system whose loop transfer function has only poles. In addition, it is applicable only if the plot is plotted on an ordinary graph sheet.
9.3 Construction of Polar Plot
The construction of polar plot can be illustrated by considering the generalized form of loop transfer function as

where ![]() are real constants,
are real constants,
![]() is the number of zeros at the origin,
is the number of zeros at the origin,
![]() is the number of poles at the origin or the type of the system,
is the number of poles at the origin or the type of the system,
![]() is the number of simple poles existing in the system,
is the number of simple poles existing in the system,
![]() is the number of simple zeros existing in the system,
is the number of simple zeros existing in the system,
![]() is the number of complex poles existing in the system,
is the number of complex poles existing in the system,
![]() is the number of complex zeros existing in the system and
is the number of complex zeros existing in the system and
![]() is the time delay in seconds.
is the time delay in seconds.
Substituting ![]() in the above equation and simplifying, we obtain
in the above equation and simplifying, we obtain
 (9.1)
(9.1)
Its magnitude is
 (9.2)
(9.2)
and the phase angle is
 (9.3)
(9.3)
where the magnitude of the term ![]() is 1 and phase angle of the term
is 1 and phase angle of the term ![]() is
is ![]() .
.
From Eqn. (9.1), it is clear that the open-loop transfer function ![]() may contain the combination of any of the following five factors:
may contain the combination of any of the following five factors:
- Constant K
- Zeros at the origin
 and poles at the origin
and poles at the origin 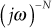
- Simple zero
 and simple pole
and simple pole 
- Complex zero
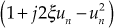 and complex pole
and complex pole 
- Transportation lag

Hence, it is necessary to have a complete study of magnitude and phase angle of these factors that can be utilized in constructing the polar plot of a composite loop transfer function ![]() . The polar plot for the loop transfer function
. The polar plot for the loop transfer function ![]() is constructed by determining its magnitude and phase angle. The magnitude and phase angle of the loop transfer function can be obtained by the multiplication of magnitudes and addition of the phase angles of individual factors present in the function.
is constructed by determining its magnitude and phase angle. The magnitude and phase angle of the loop transfer function can be obtained by the multiplication of magnitudes and addition of the phase angles of individual factors present in the function.
Also, if the polar plot of ![]() is to be plotted on an ordinary graph, the magnitude and phase angle of
is to be plotted on an ordinary graph, the magnitude and phase angle of ![]() obtained at different frequencies are converted to the real and imaginary parts of
obtained at different frequencies are converted to the real and imaginary parts of ![]() . Hence, it becomes necessary to determine the magnitude and phase angle of each factor which can be possibly present in a system.
. Hence, it becomes necessary to determine the magnitude and phase angle of each factor which can be possibly present in a system.
Factor 1: Constant ![]()
The constant ![]() is independent of frequency
is independent of frequency ![]() and hence the magnitude and phase angle of the factor are:
and hence the magnitude and phase angle of the factor are:
Magnitude : ![]()
Phase angle : ![]()
In addition, the real and imaginary parts of constant K are K and 0 respectively.
Since the magnitude, real part and imaginary part of constant K are independent of frequency, the polar plot of constant ![]() is a point on both polar graph and ordinary graph. The polar plot for constant
is a point on both polar graph and ordinary graph. The polar plot for constant ![]() on polar graph and on an ordinary graph is shown in Figs. 9.3(a) and (b) respectively.
on polar graph and on an ordinary graph is shown in Figs. 9.3(a) and (b) respectively.

Fig. 9.3 ∣ Polar plot for constant K
Factor 2: Zeros at the origin ![]() and poles at the origin
and poles at the origin ![]()
The zeros at the origin ![]() and poles at the origin
and poles at the origin ![]() are dependent on frequency
are dependent on frequency ![]() . Hence, the magnitude and phase angle when one pole or zero exists at the origin are given in Table 9.1(a).
. Hence, the magnitude and phase angle when one pole or zero exists at the origin are given in Table 9.1(a).
Since the magnitude and phase angle of the factors are dependent on frequency ![]() , the polar plot for the factor on polar graph can be drawn with the help of Table 9.1(a).
, the polar plot for the factor on polar graph can be drawn with the help of Table 9.1(a).
Table 9.1(a) ∣ Magnitude and Phase angle for jω and (jω)−1 for different values of frequency ω

The polar plot for ![]() and
and ![]() on polar graph is shown in Figs. 9.4(a) and (b) respectively.
on polar graph is shown in Figs. 9.4(a) and (b) respectively.

Fig. 9.4 ∣ Polar plot for ![]() and
and ![]() on polar graph
on polar graph
When more than one pole or zero exist at the origin, the changes to be done in plotting the polar plot on polar graph is given in Table 9.1(b).
Table 9.1(b) ∣ Magnitude and phase angle of ![]() and
and ![]()

When more than one pole or zero exist at the origin, the changes to be done in plotting the polar plot on an ordinary graph are not as easy as they are on polar graph. The reason is that depending on ![]() and
and ![]() , the real and imaginary parts vary. For example, if
, the real and imaginary parts vary. For example, if ![]() the real part is zero, whereas if
the real part is zero, whereas if ![]() the imaginary part is zero.
the imaginary part is zero.
Therefore, the polar plot for different values of ![]() and
and ![]() rotates by
rotates by ![]() either in the clockwise direction or in the anticlockwise direction on an ordinary graph. The polar plots of
either in the clockwise direction or in the anticlockwise direction on an ordinary graph. The polar plots of ![]() for different values of
for different values of ![]() on an ordinary graph are shown in Figs. 9.4(c) through (f).
on an ordinary graph are shown in Figs. 9.4(c) through (f).
Similarly, the polar plot of ( jω)-N for different values of N can be drawn on an ordinary graph. In addition, the polar plots of ( jω)Z and ( jω)-N for different values of Z and N can be drawn on polar graph.

Fig. 9.4 ∣ Polar plot for different values of ![]()
It can be noted that if the polar plot of ![]() is drawn on an ordinary graph and it is rotated by
is drawn on an ordinary graph and it is rotated by ![]() in the clockwise or anticlockwise direction, the polar plot of
in the clockwise or anticlockwise direction, the polar plot of ![]() can be obtained, provided
can be obtained, provided ![]() .
.
Factor 3: Simple zero (1 + jωT) and simple pole (1 + jωT)−1
The simple zero ![]() and simple pole
and simple pole ![]() are dependent on frequency
are dependent on frequency ![]() . Hence, the magnitude and phase angle of simple zero and simple pole are given in Table 9.2.
. Hence, the magnitude and phase angle of simple zero and simple pole are given in Table 9.2.
Since the magnitude and phase angle are dependent on frequency ![]() , the polar plot for a simple zero and simple pole on polar graph can be drawn using Table 9.2.
, the polar plot for a simple zero and simple pole on polar graph can be drawn using Table 9.2.
Table 9.2 ∣ Magnitude and Phase angle for ![]() and
and ![]() for different values of frequency ω
for different values of frequency ω

The polar plots for ![]() and
and ![]() on the polar graph are shown in Figs. 9.5(a) and (b) respectively.
on the polar graph are shown in Figs. 9.5(a) and (b) respectively.

Fig. 9.5 ∣ Polar plot for ![]() and
and ![]() on polar graph
on polar graph
Factor 4: Complex zero (1 + j2ξun − un2) and complex pole (1 + j2ξun − un2)−1
The complex zero ![]() and complex pole
and complex pole ![]() are dependent on frequency
are dependent on frequency ![]() . Hence, the magnitude and phase angle of the factors are given in Table 9.3(a).
. Hence, the magnitude and phase angle of the factors are given in Table 9.3(a).
Table 9.3(a) ∣ Magnitude and phase angle of ![]() and
and ![]()

In Table 9.3(a), ![]() is the damping ratio and
is the damping ratio and ![]() .
.
Since the magnitude and phase angle of the factors are dependent on frequency ![]() , the polar plot for the factor on the polar graph can be drawn using Table 9.3(b).
, the polar plot for the factor on the polar graph can be drawn using Table 9.3(b).
Table 9.3(b) ∣ Magnitude and Phase angle for ![]() and
and ![]() for different values of frequency ω
for different values of frequency ω

The polar plots for ![]() and
and ![]() on the polar graphs for different values of
on the polar graphs for different values of ![]() are shown in Figs. 9.6(a) and (b) respectively.
are shown in Figs. 9.6(a) and (b) respectively.

Fig. 9.6 ∣ Polar plots for ![]() and
and ![]() on the polar graph
on the polar graph
Factor 5: Transportation lag ![]()
The factor ![]() can be rewritten as
can be rewritten as ![]() . The magnitude and phase angle of the factor are
. The magnitude and phase angle of the factor are
Magnitude of ![]()
and Phase angle = 
But the phase angle obtained is in the unit of radians. Therefore, the phase angle in degrees is obtained as
![]()

Fig. 9.7 ∣ Polar plot of transportation lag
Since the magnitude of the factor is independent of frequency ![]() , the polar plot for the factor on polar graph and on an ordinary graph is a unit circle, which are shown in Figs. 9.7(a) and (b) respectively.
, the polar plot for the factor on polar graph and on an ordinary graph is a unit circle, which are shown in Figs. 9.7(a) and (b) respectively.
9.4 Determination of Frequency Domain Specification from Polar Plot
The different frequency domain specifications such as gain margin, phase margin, phase crossover frequency and gain crossover frequency can be determined by using polar plot. As the polar plots can be plotted both on polar graph and ordinary graph, the determination of frequency domain specification also differs.
9.4.1 Gain Crossover Frequency ωgc
It is the frequency at which the magnitude of the loop transfer function ![]() is unity. This frequency can be obtained by substituting random frequencies in Eqn. (9.2). But by this process, we can obtain only an approximate value of frequency and also this process is time-consuming. Hence, there exist two alternate methods for determining
is unity. This frequency can be obtained by substituting random frequencies in Eqn. (9.2). But by this process, we can obtain only an approximate value of frequency and also this process is time-consuming. Hence, there exist two alternate methods for determining ![]() which are discussed below:
which are discussed below:
Method 1: It is known that ![]() = 1 at
= 1 at ![]() . Also, Eqn. (9.2) is a function of frequency. Therefore, by solving the equation, we obtain
. Also, Eqn. (9.2) is a function of frequency. Therefore, by solving the equation, we obtain ![]() . This method consumes more time.
. This method consumes more time.
Method 2: From the polar plot drawn on the polar graph, it is easy to determine the ![]() when
when ![]() . Substituting the obtained angle in Eqn. (9.3) and using
. Substituting the obtained angle in Eqn. (9.3) and using ![]() , it is easy to determine
, it is easy to determine ![]() .
.
Hence, method 2 is used in this chapter for determining the gain crossover frequency ![]() when a polar plot for a loop transfer function is drawn.
when a polar plot for a loop transfer function is drawn.
9.4.2 Phase Crossover Frequency ωpc
It is the frequency at which the phase angle of the loop transfer function ![]() is
is ![]() or
or ![]() . This frequency
. This frequency ![]() can be obtained by substituting random frequencies in Eqn. (9.3). But by this process, we can obtain only an approximate value of frequency and also this process is a time-consuming one. Hence, an alternate method exists for determining
can be obtained by substituting random frequencies in Eqn. (9.3). But by this process, we can obtain only an approximate value of frequency and also this process is a time-consuming one. Hence, an alternate method exists for determining ![]() as discussed below:
as discussed below:
Alternate method
It is known that ![]() at
at ![]() . Hence, using
. Hence, using ![]() , the value of
, the value of ![]() can be determined.
can be determined.
9.4.3 Gain Margin gm
The gain margin ![]() of the system obtained by taking the inverse of the magnitude of
of the system obtained by taking the inverse of the magnitude of ![]() at phase crossover frequency
at phase crossover frequency ![]() .
.

9.4.4 Phase Margin pm
The phase margin ![]() of the system is obtained by
of the system is obtained by
![]()
9.5 Procedure for Constructing Polar Plot
The flow chart for constructing the polar plot of a system on a polar graph is shown in Fig. 9.8(a).

Fig. 9.8(a) ∣ Flow chart for constructing the polar plot on polar graph
The flowchart for constructing the polar plot of a system on an ordinary graph is shown in Fig. 9.8(b).

Fig. 9.8(b) ∣ Flow chart for constructing the polar plot on an ordinary graph
Intersection of polar plot for a system
If the polar plot intersects ![]() line on a polar graph, it implies that the polar plot intersects the positive real axis line on an ordinary graph. Therefore, there exists a relation between the intersection points on an ordinary graph and on a polar graph which is listed in Table 9.4.
line on a polar graph, it implies that the polar plot intersects the positive real axis line on an ordinary graph. Therefore, there exists a relation between the intersection points on an ordinary graph and on a polar graph which is listed in Table 9.4.
Table 9.4 ∣ Relation between intersection points

In addition, it is to be noted that if ![]() number of intersection points exists in plotting the polar plot on a polar graph, same number of intersection points exists in plotting the polar plot on an ordinary graph.
number of intersection points exists in plotting the polar plot on a polar graph, same number of intersection points exists in plotting the polar plot on an ordinary graph.
9.6 Typical Sketches of Polar Plot on an Ordinary Graph and Polar Graph
The typical sketches of polar plot on an ordinary and polar graph based on the type and order of a system are given below.
Type 0 Order 2 System
Let the loop transfer function of Type 0 Order 2 system be
![]()
Substituting ![]() , we obtain
, we obtain
![]()
The magnitude and phase angle of the system are given by

and
![]()
The magnitude and phase angle at ![]() and
and ![]() are given in Table 9.5.
are given in Table 9.5.
Table 9.5 ∣ Magnitude and phase angle of the system

To determine the intersection point on real and imaginary axis
The real and imaginary part of loop transfer function can be determined as


Therefore, real part of loop transfer function 
and imaginary part of loop transfer function 
Intersection point on imaginary axis
Step 1: Equating the real part of loop transfer function to zero and determining the frequency ![]() i.e.,
i.e., ![]() .
.
Therefore, 
Upon solving, we obtain

Step 2: Substituting  in the imaginary part of loop transfer function, we obtain the intersection of the polar plot on imaginary axis.
in the imaginary part of loop transfer function, we obtain the intersection of the polar plot on imaginary axis.
Intersection point on imaginary axis = ![]()
Substituting  in
in  , we obtain
, we obtain
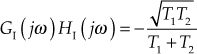
Step 3: Therefore, magnitude and phase angle of loop transfer function at  is
is
Magnitude 
and Phase angle ![]()
Using the magnitude and phase angle at different frequencies, we can determine the real and imaginary parts of the loop transfer function as given in Table 9.6.
Table 9.6 ∣ Real and imaginary parts of the system

Using Table 9.6, the polar plot of TYPE 0 ORDER 2 system on an ordinary graph is shown in Fig. 9.9(a).

Fig. 9.9(a) ∣ Polar plot of the system
The magnitude and phase angle at different frequencies are given in Table 9.7.
Table 9.7 ∣ Magnitude and phase angle

Using Table 9.7, the polar plot of TYPE 0 ORDER 2 system on polar graph is shown in Fig. 9.9(b).

Fig. 9.9(b) ∣ Polar plot of the system
Similarly, the polar plot on a polar graph and intersection points on the different axes for different systems can be determined.
9.7 Stability Analysis using Polar Plot
The stability of a system can be examined from the polar plot once the frequency domain specifications are obtained. The stability of the system can be analyzed by using the crossover frequencies (![]() and
and ![]() ) or the gain and phase margins.
) or the gain and phase margins.
9.7.1 Based on Crossover Frequencies
A system can either be a stable system or marginally stable system or unstable system. The stability of the system based on the relation between crossover frequencies is given in Table 9.8.
Table 9.8 ∣ Stability of the system based on crossover frequencies

9.7.2 Based on Gain Margin and Phase Margin
The stability of a system based on the gain margin and phase margin is given in Table 9.9.
Table 9.9 ∣ Stability of the system based on ![]() and
and ![]()

But the problem that exists in examining the stability of the system from polar plot is the determination of ![]() and
and ![]() which is a tedious process. Hence, an alternate way of examining the stability of the system using polar plot exists, which does not require the determination of
which is a tedious process. Hence, an alternate way of examining the stability of the system using polar plot exists, which does not require the determination of ![]() and
and ![]() is discussed in the following section.
is discussed in the following section.
9.7.3 Based on the Location of Phase Crossover Point
Consider the polar plot of a loop transfer function drawn on an ordinary graph as shown in Fig. 9.10.
Let ![]() and
and ![]() be the points on the polar plot when the plot crosses the real axis and unit circle as shown in Fig. 9.10. Using Table 9.5, the points
be the points on the polar plot when the plot crosses the real axis and unit circle as shown in Fig. 9.10. Using Table 9.5, the points ![]() and
and ![]() are called phase crossover and gain crossover points respectively. Let the frequency
are called phase crossover and gain crossover points respectively. Let the frequency ![]() at the point
at the point ![]() is the phase crossover frequency
is the phase crossover frequency ![]() and magnitude of the loop transfer function at the point
and magnitude of the loop transfer function at the point ![]() be
be ![]()

Fig. 9.10 ∣ Polar plot of a loop transfer function in an ordinary graph
Now, based on the location of point ![]() , the stability of the system can be examined. The stability of the system based on the location of point
, the stability of the system can be examined. The stability of the system based on the location of point ![]() is listed in Table 9.10.
is listed in Table 9.10.
Table 9.10 ∣ Stability of the system based on phase crossover point, ![]()

9.8 Determining the Gain K from the Desired Frequency Domain Specifications
The frequency domain specifications for which the gain ![]() can be determined are gain margin and phase margin. The procedure for determining the gain
can be determined are gain margin and phase margin. The procedure for determining the gain ![]() for the desired
for the desired ![]() and
and ![]() using polar plot is not so tedious as it was using Bode plot. The following sections describe how the gain
using polar plot is not so tedious as it was using Bode plot. The following sections describe how the gain ![]() can be determined for desired
can be determined for desired ![]() and
and ![]() using polar plot.
using polar plot.
9.8.1 When the Desired Gain Margin of the System is Specified
The step-by-step procedure to determine the gain ![]() for a specified gain margin is explained below:
for a specified gain margin is explained below:
Step 1: Assume ![]() for the given loop transfer function and construct the polar plot of the system either on the polar graph or on the ordinary graph.
for the given loop transfer function and construct the polar plot of the system either on the polar graph or on the ordinary graph.
Step 2: Determine the phase crossover point, ![]() from the polar plot. If the polar plot is plotted on the polar graph, the point
from the polar plot. If the polar plot is plotted on the polar graph, the point ![]() refers to the point at which the polar plot crosses
refers to the point at which the polar plot crosses ![]() line and if the polar plot is plotted on the ordinary graph, the point
line and if the polar plot is plotted on the ordinary graph, the point ![]() refers to the point at which the polar plot crosses negative real axis.
refers to the point at which the polar plot crosses negative real axis.
Step 3: Determine the magnitude of the loop transfer function at ![]() from the polar plot. Let it be
from the polar plot. Let it be ![]() .
.
Step 4: Let the desired gain margin of the system be ![]() dB. Let
dB. Let ![]() be the phase crossover point on the polar plot corresponding to
be the phase crossover point on the polar plot corresponding to ![]() . The magnitude of the loop transfer function at
. The magnitude of the loop transfer function at ![]() can be determined by using
can be determined by using ![]()
Step 5: Now, the gain ![]() for the desired gain margin can be determined as
for the desired gain margin can be determined as

Step 6: With the gain ![]() , the new polar plot can be drawn. The polar plot for different values of
, the new polar plot can be drawn. The polar plot for different values of ![]() is shown in Fig. 9.11(a).
is shown in Fig. 9.11(a).

Fig. 9.11(a) ∣ Polar plot for different values of ![]()
9.8.2 When the Desired Phase Margin of the System is Specified
The step-by-step procedure to determine the gain ![]() for a specified phase margin is explained below:
for a specified phase margin is explained below:
Step 1: Assume ![]() for the given loop transfer function and construct the polar plot of the system either on the polar graph or on the ordinary graph.
for the given loop transfer function and construct the polar plot of the system either on the polar graph or on the ordinary graph.
Step 2: Determine the gain crossover point, ![]() from the polar plot. If the polar plot is plotted on the polar graph or on the ordinary graph, the point
from the polar plot. If the polar plot is plotted on the polar graph or on the ordinary graph, the point ![]() refers to the point at which the polar plot crosses unity circle.
refers to the point at which the polar plot crosses unity circle.
Step 3: Determine the magnitude of the loop transfer function at ![]() from the polar plot. Let it be
from the polar plot. Let it be ![]() .
.
Step 4: Let the desired phase margin of the system be ![]() dB. Let
dB. Let ![]() be the gain crossover point on the polar plot corresponding to
be the gain crossover point on the polar plot corresponding to ![]() .
.
Step 5: Determine the phase angle of the system corresponding to ![]() . Let it be
. Let it be ![]() deg. The value of
deg. The value of ![]() is determined by using,
is determined by using, ![]() .
.
Step 6: Draw a radial line using ![]() deg from origin that cuts the polar plot of the loop transfer function
deg from origin that cuts the polar plot of the loop transfer function ![]() with
with ![]() at
at ![]() . The magnitude of the loop transfer function at
. The magnitude of the loop transfer function at ![]() can be determined from the polar plot and let it be
can be determined from the polar plot and let it be ![]() .
.
Step 7: Now, the gain ![]() for the desired gain margin can be determined as
for the desired gain margin can be determined as

Step 8: With the gain ![]() , the new polar plot can be drawn. The polar plot for different values of
, the new polar plot can be drawn. The polar plot for different values of ![]() is shown in Fig. 9.11(b).
is shown in Fig. 9.11(b).

Fig. 9.11(b) ∣ Polar plot for different values of ![]()
Example 9.1: The loop transfer function of a system is ![]() . Sketch the polar plot for the system.
. Sketch the polar plot for the system.
Solution:
- The loop transfer function of the system
 .
.

Fig. E9.1
- Substituting
 in the loop transfer function, we obtain
in the loop transfer function, we obtain

- The only one corner frequency existing in the system is
 rad/sec.
rad/sec. - The magnitude and phase angle of the system are

and

- For different values of frequency
 , the magnitude and phase angle of the system are calculated and tabulated in Table E9.1.
, the magnitude and phase angle of the system are calculated and tabulated in Table E9.1.
Table E9.1 ∣ Magnitude and phase angle of the system
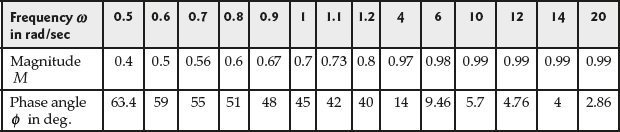
The polar plot of the given system using Table E9.1 is shown in Fig. E9.1.
Example 9.2: The loop transfer function of a system is  . Sketch the polar plot for the system.
. Sketch the polar plot for the system.
Solution:
- The loop transfer function of the system
 .
. - Substituting
 and
and  in the loop transfer function, we obtain
in the loop transfer function, we obtain

- The three corner frequencies existing in the system are
 rad/sec,
rad/sec,  rad/sec and
rad/sec and  rad/sec
rad/sec
Fig. E9.2 ∣ Polar plot for

- The magnitude and phase angle of the system are

and

- For different values of frequency
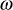 , the magnitude and phase angle of the system are calculated and tabulated in Table E9.2.
, the magnitude and phase angle of the system are calculated and tabulated in Table E9.2.
Table E9.2 ∣ Magnitude and phase angle of the system

The polar plot of the given system using Table E9.2 is shown in Fig. E9.2.
Example 9.3: The loop transfer function of a unity feedback system is given by  . Sketch the polar plot for the system.
. Sketch the polar plot for the system.
Solution:
- The loop transfer function of a system is
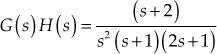 .
. - Substituting
 , we obtain
, we obtain

- The three corner frequencies existing in the system are
 rad/sec,
rad/sec, 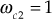 rad/sec and
rad/sec and  rad/sec.
rad/sec. - The magnitude and phase angle of the system are

and


Fig. E9.3 ∣ Polar plot for

- For different values of frequency
 , the magnitude and phase angle of the system are calculated and tabulated in Table E9.3.
, the magnitude and phase angle of the system are calculated and tabulated in Table E9.3.
Table E9.3 ∣ Magnitude and phase angle of the system

The polar plot of the given system using the data in Table E9.3 is shown in Fig. E9.3.
Example 9.4: The loop transfer function of a unity feedback system is given by 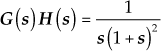 . Sketch the polar plot for the system and determine the gain and phase margin of the system.
. Sketch the polar plot for the system and determine the gain and phase margin of the system.
Solution:
- The loop transfer function of a system is
 .
. - Substituting
 , we obtain
, we obtain

- The corner frequency of the given system is
 rad/sec.
rad/sec. - The magnitude and phase angle of the system are

and

- For different values of frequency
 , the magnitude and phase angle of the system are calculated and tabulated in Table E9.4.
, the magnitude and phase angle of the system are calculated and tabulated in Table E9.4.
Table E9.4 ∣ Magnitude and phase angle of the system

The polar plot of the given system using Table E9.4 is shown in Fig. E9.4.

Fig. E9.4
Determination of Gain Margin and Phase Margin
The gain margin and phase margin of the system are calculated at phase crossover frequency and gain crossover frequency respectively. The phase crossover frequency is the frequency at which the phase angle of the system is ![]() or
or ![]() . Also, the gain crossover frequency is the frequency at which the magnitude of the system is 1.
. Also, the gain crossover frequency is the frequency at which the magnitude of the system is 1.
Using the above definition and Table E9.4, we obtain
Gain crossover frequency ![]() rad/sec and Phase crossover frequency
rad/sec and Phase crossover frequency ![]() rad/sec.
rad/sec.
Hence, gain margin and phase margin of the system are given by
Gain margin, 
and Phase margin, ![]()
Example 9.5: The loop transfer function of a unity feedback system is given by ![]() . Sketch the polar plot for the system.
. Sketch the polar plot for the system.
Solution:
- The loop transfer function of a system is

- Substituting
 , we obtain
, we obtain
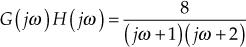
- The two corner frequencies existing in the given system are
 rad/sec and
rad/sec and  rad/sec respectively.
rad/sec respectively. - The magnitude and phase angle of the system are

and

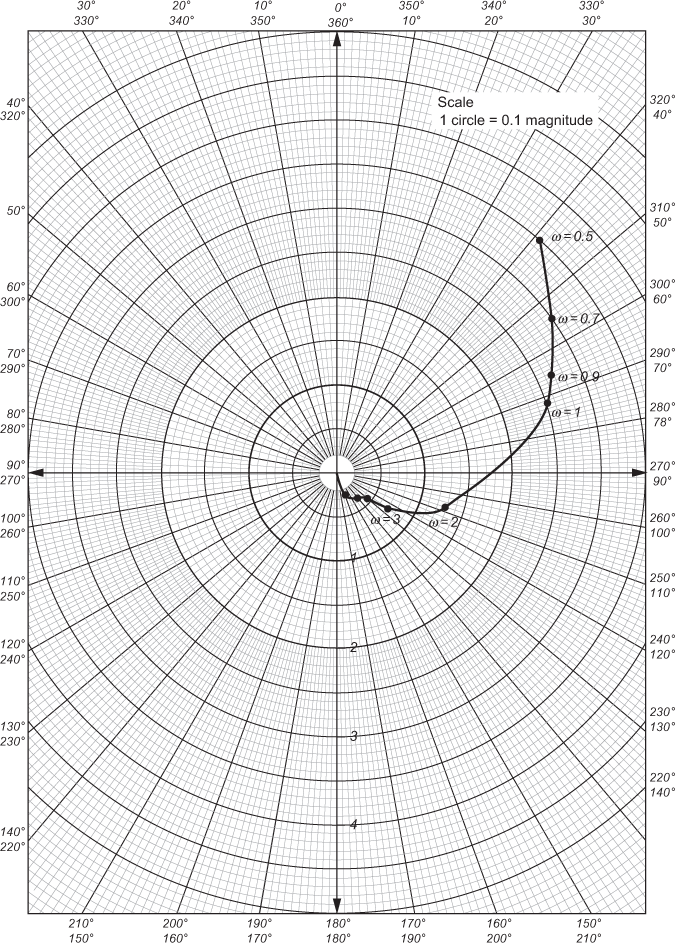
Fig. E9.5
- For different values of frequency
 , the magnitude and phase angle of the system are calculated and tabulated in Table E9.5.
, the magnitude and phase angle of the system are calculated and tabulated in Table E9.5.
Table E9.5 ∣ Magnitude and phase angle of the system

The polar plot of the given system using the data in Table E9.5 is shown in Fig. E9.5.
9.9 Introduction to Nyquist Stability Criterion
The Routh–Hurwitz criterion and root locus methods are used to determine the stability of the linear single-input single-output (SISO) system by finding the location of the roots of the characteristic equation in s-plane. The Nyquist stability criterion derived by H. Nyquist is a semi-graphical method that helps in determining the absolute stability of the closed-loop system graphically from frequency response of loop transfer function (Nyquist plot) without determining the closed-loop poles. The Nyquist plot of a loop transfer function ![]() is a graphical representation of the frequency response analysis when the frequency
is a graphical representation of the frequency response analysis when the frequency ![]() is varied from
is varied from ![]() to
to ![]() . Since most of the linear control systems are analyzed by using their frequency responses, Nyquist plot will be convenient in determining the stability of the system.
. Since most of the linear control systems are analyzed by using their frequency responses, Nyquist plot will be convenient in determining the stability of the system.
9.10 Advantages of Nyquist Plot
The advantages of Nyquist plot are:
- Nyquist plot helps in determining the relative stability of the system in addition to the absolute stability of the system.
- It determines the stability of the closed-loop system from open-loop transfer function without calculating the roots of characteristic equation.
- It gives the degree of instability of an unstable system and indicates the ways in which the stability of the system can be improved.
- It gives information related to frequency domain characteristics such as
 , BW etc..
, BW etc.. - It can easily be applied to systems with pure time delay that cannot be analyzed using root locus method or Routh–Hurwitz criterion.
9.11 Basic Requirements for Nyquist Stability Criterion
The Nyquist stability criterion will be useful in analyzing the stability of both the open-loop and closed-loop systems. The concepts such as encirclement, enclosement, number of encirclements around a point, mapping from one plane to another plane and principle of argument are important to study the Nyquist stability criterion of a system.
9.12 Encircled and Enclosed
The concept of encircled and enclosed will be helpful to interpret the Nyquist plot for analyzing the stability of the system.
9.12.1 Encircled
A point or region in a complex function plane is said to be encircled by a closed path if the particular point or region is found inside the closed path irrespective of the direction of closed path. All other points existing outside the closed path is not encircled. The concept of encirclement with two different points and different directions of closed path is shown in Figs. 9.12(a) and (b).

Fig. 9.12 ∣ Encirclement concept
Irrespective of the direction of closed path, the point A shown in Figs. 9.12(a) and (b) is encircled and it is found inside the path. Since the point B shown in Figs. 9.12(a) and (b) lies outside the closed path, the point B is not encircled.
9.12.2 Enclosed
A point or region in a complex function plane is said to be enclosed by a closed path if the point or region is encircled by the closed path or if the point or region lies to the left of the closed path when the path is traversed in the counter clockwise (CCW) direction.
In addition, a point or region in a complex function plane is said to be enclosed by a closed path if the point or region is not encircled by the closed path or it lies to the left of the closed path when the path is traversed in the clockwise (CW) direction. The concept of enclosement with two different points and different directions of closed path is shown in Figs. 9.13(a) and (b) respectively.

Fig. 9.13 ∣ Enclosement concept
The point A in Fig.9.13(a) and point B in Fig. 9.13(b) is enclosed by the closed path.
9.13 Number of Encirclements or Enclosures
Let ![]() be the number of encirclements or enclosures for a point, when the point is encircled or enclosed by the closed path. The sign of
be the number of encirclements or enclosures for a point, when the point is encircled or enclosed by the closed path. The sign of ![]() depends on the direction of closed path. If the closed path is in the clockwise direction, it is
depends on the direction of closed path. If the closed path is in the clockwise direction, it is ![]() ; and if the closed path is in the counter clockwise direction, it is
; and if the closed path is in the counter clockwise direction, it is ![]() . The magnitude of
. The magnitude of ![]() is determined as follows:
is determined as follows:
- Consider an arbitrary point
 on the closed path.
on the closed path. - Let the point
 follow the closed path in the direction of closed path until it reaches the starting point.
follow the closed path in the direction of closed path until it reaches the starting point.
Now, ![]() is the net number of revolutions traversed by the arbitrary point
is the net number of revolutions traversed by the arbitrary point ![]() or the number of encirclements/enclosures for a point. For example, consider two points
or the number of encirclements/enclosures for a point. For example, consider two points ![]() and
and ![]() as shown in Figs. 9.14(a) and (b) in
as shown in Figs. 9.14(a) and (b) in ![]() -plane.
-plane.

Fig. 9.14 ∣ Number of encirclement concept
From Fig. 9.14(a), it is clear that the point A and B are encircled by the closed path and from Fig. 9.14(b), it is clear that the point A and B are enclosed by the closed path. Therefore, the net number of revolutions traversed by ![]() around the point A in Figs. 9.14(a) and (b) is
around the point A in Figs. 9.14(a) and (b) is ![]() and
and ![]() respectively. Similarly, the net number of revolutions traversed by
respectively. Similarly, the net number of revolutions traversed by ![]() around the point B in Figs. 9.14(a) and (b) is
around the point B in Figs. 9.14(a) and (b) is ![]() and
and ![]() respectively.
respectively.
9.14 Mapping of s-Plane into Characteristic Equation Plane
The mapping of ![]() -plane into characteristic equation plane will be helpful in mapping
-plane into characteristic equation plane will be helpful in mapping ![]() -plane into
-plane into ![]() -plane which is the basic Nyquist stability criterion for analyzing the stability of the open-loop and closed-loop systems.
-plane which is the basic Nyquist stability criterion for analyzing the stability of the open-loop and closed-loop systems.
Consider a simple closed-loop system as shown in Fig. 9.15.

Fig. 9.15 ∣ A simple closed-loop system
The closed-loop transfer function of the system is  (9.5)
(9.5)
and the characteristic equation of the system is ![]() (9.6)
(9.6)
where ![]() is the forward path transfer function,
is the forward path transfer function, ![]() is the feedback path transfer function and
is the feedback path transfer function and ![]() is the loop transfer function of the system.
is the loop transfer function of the system.
The general form of the loop transfer function is given by
 (9.7)
(9.7)
and ![]() is the time delay in seconds.
is the time delay in seconds.
Substituting Eqn. (9.7) in Eqn. (9.6), we obtain
 (9.8)
(9.8)
Since ![]() is a complex quantity, the function
is a complex quantity, the function ![]() is also a complex quantity that can be defined as
is also a complex quantity that can be defined as ![]() and represented on the complex
and represented on the complex ![]() -plane with
-plane with ![]() and
and ![]() as the co-ordinates. Equations (9.7) and (9.8) indicate that for every point in
as the co-ordinates. Equations (9.7) and (9.8) indicate that for every point in ![]() -plane at which
-plane at which ![]() exists, we can determine a point in the
exists, we can determine a point in the ![]() -plane. Therefore, if a contour exists in the
-plane. Therefore, if a contour exists in the ![]() -plane and does not go through any pole or zero of
-plane and does not go through any pole or zero of ![]() , a corresponding contour will exist in the
, a corresponding contour will exist in the ![]() -plane. These contours will be helpful in determining the stability of the system using Nyquist stability criterion.
-plane. These contours will be helpful in determining the stability of the system using Nyquist stability criterion.
Consider a characteristic equation of a system as ![]() (only one pole) and a contour in
(only one pole) and a contour in ![]() -plane as shown in Fig. 9.16(a). From Fig. 9.16(a), it is clear that, as the contour in
-plane as shown in Fig. 9.16(a). From Fig. 9.16(a), it is clear that, as the contour in ![]() -plane encloses
-plane encloses ![]() (a singular point), a contour which encloses the origin will exist in
(a singular point), a contour which encloses the origin will exist in ![]() -plane.
-plane.

Fig. 9.16(a) ∣ A contour in ![]() -plane
-plane
Table 9.11 is used for transforming the contour in ![]() -plane to a contour in
-plane to a contour in ![]() -plane.
-plane.
Table 9.11 ∣ Transforming the contour from s-plane into F(s)-plane

The contour in ![]() -plane that is obtained using
-plane that is obtained using ![]() -plane is shown in Fig. 9.16(b).
-plane is shown in Fig. 9.16(b).

Fig. 9.16(b) ∣ Contour in F(s)-plane
The conclusion obtained from Figs. 9.16(a) and (b) is that if the contour in ![]() -plane encloses a single pole and moves in the clockwise direction, then the contour in
-plane encloses a single pole and moves in the clockwise direction, then the contour in ![]() -plane will encircle the origin once in the counter clockwise direction.
-plane will encircle the origin once in the counter clockwise direction.
Similarly, if the contour in ![]() -plane encloses a
-plane encloses a ![]() poles and moves in the clockwise direction, then the contour in
poles and moves in the clockwise direction, then the contour in ![]() -plane will encircle the origin m-times in the counter clockwise direction. Table 9.11 shows the mapping of different
-plane will encircle the origin m-times in the counter clockwise direction. Table 9.11 shows the mapping of different ![]() -plane contour to the
-plane contour to the ![]() -plane contour.
-plane contour.
9.15 Principle of Argument
The principle of arguments will be useful in examining the stability of the system based on the Nyquist stability criterion. Its value is based on the mapping of contour from ![]() -plane to the
-plane to the ![]() -plane. The principle of argument can be stated as follows:
-plane. The principle of argument can be stated as follows:
Let ![]() be the number of zeros and
be the number of zeros and ![]() be the number of poles of the characteristic equation encircled by the
be the number of poles of the characteristic equation encircled by the ![]() -plane contour, then the number of encirclements
-plane contour, then the number of encirclements ![]() made by the
made by the ![]() -plane contour around the origin can be obtained as the difference between
-plane contour around the origin can be obtained as the difference between ![]() and
and ![]()
The principle of argument in equation form can be obtained as
![]() (9.9)
(9.9)
where
![]() is the number of encirclements made by the
is the number of encirclements made by the ![]() -plane contour around the origin,
-plane contour around the origin,
![]() is the number of zeros of characteristic equation encircled by
is the number of zeros of characteristic equation encircled by ![]() -plane contour and
-plane contour and
![]() is the number of poles of characteristic equation encircled by
is the number of poles of characteristic equation encircled by ![]() -plane contour.
-plane contour.
The principle of argument can be graphically proved when ![]() of the system is represented in terms of polar co-ordinates (in terms of magnitude and phase angle) as explained below.
of the system is represented in terms of polar co-ordinates (in terms of magnitude and phase angle) as explained below.
Consider 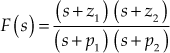 , where
, where ![]() is a zero of
is a zero of ![]() and
and ![]() is a pole of
is a pole of ![]() and a contour with an arbitrary point
and a contour with an arbitrary point ![]() as shown in Fig. 9.17.
as shown in Fig. 9.17.

Fig. 9.17 ∣ Contour in ![]() -plane with poles and zeros
-plane with poles and zeros
Then, ![]() in polar co-ordinates can be obtained as
in polar co-ordinates can be obtained as

![]() (9.10)
(9.10)
The function ![]() at
at ![]() is given by
is given by
 (9.11)
(9.11)
Each factor present in Eqn. (9.11) can be represented graphically by the vector drawn from poles or zeros to the arbitrary point ![]() as shown in Fig. 9.18(a) which in turn represents
as shown in Fig. 9.18(a) which in turn represents ![]() as shown in Fig. 9.18(b).
as shown in Fig. 9.18(b).

Fig. 9.18 ∣ Relation between ![]() -plane and
-plane and ![]() -plane
-plane
If the arbitrary point ![]() moves in the contour in the specified direction, then the angles generated by the vectors drawn from poles and zeros at
moves in the contour in the specified direction, then the angles generated by the vectors drawn from poles and zeros at ![]() can be determined till the arbitrary point reaches the initial position. The resultant angle generated by the poles and zeros that are not encircled by the contour and zero which is encircled by the contour will be
can be determined till the arbitrary point reaches the initial position. The resultant angle generated by the poles and zeros that are not encircled by the contour and zero which is encircled by the contour will be ![]() radians if we calculate it manually. Therefore, if
radians if we calculate it manually. Therefore, if ![]() number of zeros are encircled by the contour, then the angle generated by the poles and zeros when the point
number of zeros are encircled by the contour, then the angle generated by the poles and zeros when the point ![]() completes one full rotation in the contour will be
completes one full rotation in the contour will be ![]() radians.
radians.
If the contour in ![]() -plane encloses
-plane encloses ![]() number of poles and
number of poles and ![]() number of zeros, then the net angle generated by the poles and zeros when the point
number of zeros, then the net angle generated by the poles and zeros when the point ![]() completes one full rotation in the contour will be
completes one full rotation in the contour will be
![]()
or ![]() (9.12)
(9.12)
where ![]() is the angle made by the contour in
is the angle made by the contour in ![]() -plane which is shown in Fig. 9.13(b).
-plane which is shown in Fig. 9.13(b).
![]() is the net number of encirclements of the origin made by the contour in
is the net number of encirclements of the origin made by the contour in ![]() -plane.
-plane.
Hence, the net number of encirclements from Eqn. (9.12) will be ![]() , which is the same as Eqn. (9.9). Table 9.12 shows the number of encirclements made by the
, which is the same as Eqn. (9.9). Table 9.12 shows the number of encirclements made by the ![]() -plane contour around the origin for different
-plane contour around the origin for different![]() -plane contours.
-plane contours.
Table 9.12 ∣ Mapping of ![]() -plane contour to the
-plane contour to the ![]() -plane contour alongwith the principle of arguments
-plane contour alongwith the principle of arguments

The conclusion obtained using Eqn. (9.9) and Table 9.12 is listed in Table 9.13.
Table 9.13 ∣ Possible outcomes of principle of arguments

9.16 Nyquist Stability Criterion
The closed-loop system is said to be a stable system if all the roots of the characteristic equation ![]() lie in the left half of the
lie in the left half of the ![]() -plane. The system is stable if all the closed-loop poles of the system or the roots of the characteristic equation lie in the left half of the
-plane. The system is stable if all the closed-loop poles of the system or the roots of the characteristic equation lie in the left half of the ![]() -plane even though the poles and zeros of the loop transfer function
-plane even though the poles and zeros of the loop transfer function ![]() lie in the right half of the
lie in the right half of the ![]() -plane. The relationship between the zeros of
-plane. The relationship between the zeros of ![]() , poles of
, poles of ![]() , characteristic equation
, characteristic equation ![]() and loop transfer function can be obtained using Eqs. (9.7) and (9.8) as follows:
and loop transfer function can be obtained using Eqs. (9.7) and (9.8) as follows:
- Zeros of
 = closed-loop poles of the system
= closed-loop poles of the system
= roots of characteristic equation
- Poles of
 = poles of loop transfer function
= poles of loop transfer function 
The two types of stability are defined as
- Open-loop stability: If all the poles of the loop transfer function
 or poles of
or poles of  lie in the left half of the
lie in the left half of the  -plane and the value is less than zero, then the system is said to an open-loop stable system.
-plane and the value is less than zero, then the system is said to an open-loop stable system. - Closed-loop stability: If all the closed-loop poles of the system or the roots of characteristic equation or zeros of
 lie in the left half of the
lie in the left half of the  -plane and their values are less than zero, then the system is said to be a closed-loop stable system.
-plane and their values are less than zero, then the system is said to be a closed-loop stable system.
If the loop transfer function of a system is given by Eqn. (9.7), just by inspection or by using Routh's criterion, it is possible to determine the number of poles which does not lie in the left half of the ![]() -plane. But determining the zeros of
-plane. But determining the zeros of ![]() or the roots of the characteristic equation of the system given by Eqn. (9.8) is difficult, if the order of the polynomial is greater than 3. Hence, to overcome these difficulties, the Nyquist stability criterion relates the frequency response of the loop transfer function
or the roots of the characteristic equation of the system given by Eqn. (9.8) is difficult, if the order of the polynomial is greater than 3. Hence, to overcome these difficulties, the Nyquist stability criterion relates the frequency response of the loop transfer function ![]() to the number of poles and zeros of
to the number of poles and zeros of ![]() which will be helpful in determining the absolute stability of the system.
which will be helpful in determining the absolute stability of the system.
9.17 Nyquist Path
The semi-circular contour path of infinite radius in the right half of the ![]() -plane with the entire
-plane with the entire ![]() axis from
axis from ![]() to
to ![]() in the clockwise direction is called as Nyquist path. This Nyquist path will be helpful in analyzing the stability of the linear control system and it encloses the entire right half of
in the clockwise direction is called as Nyquist path. This Nyquist path will be helpful in analyzing the stability of the linear control system and it encloses the entire right half of ![]() -plane and also encloses the zeros and poles of
-plane and also encloses the zeros and poles of ![]() that has positive real parts. The Nyquist path for a particular system is shown in Fig. 9.19(a). It is necessary that the Nyquist path should not pass through any poles and zeros of
that has positive real parts. The Nyquist path for a particular system is shown in Fig. 9.19(a). It is necessary that the Nyquist path should not pass through any poles and zeros of ![]() .
.

Fig. 9.19(a) ∣ Nyquist path
If the loop transfer function ![]() has a pole or poles at the origin in the
has a pole or poles at the origin in the ![]() -plane, mapping of this point will become indeterminate. Hence, a contour is taken around the origin to avoid such situations, which is shown in Fig. 9.19(b) and the zoomed view of the contour is shown in Fig. 9.19(c).
-plane, mapping of this point will become indeterminate. Hence, a contour is taken around the origin to avoid such situations, which is shown in Fig. 9.19(b) and the zoomed view of the contour is shown in Fig. 9.19(c).

Fig. 9.19 ∣ Nyquist contour for a system with a pole and/or zero at the origin
If the mapping theorem is applied to the system, then the following conclusion is made:
If the Nyquist path for a system is chosen as shown in Fig. 9.19(a), then the number of zeros of ![]() which lies in the right half of
which lies in the right half of ![]() -plane is equal to the summation of the number of poles of
-plane is equal to the summation of the number of poles of ![]() which lies in the right half of
which lies in the right half of ![]() -plane and number of clockwise encirclements of the origin made by the contour in
-plane and number of clockwise encirclements of the origin made by the contour in ![]() -plane.
-plane.
9.18 Relation Between G(s) H(s)-Plane and F(s)-Plane
We know that ![]() , which is the vector sum of the unit vector and the vector
, which is the vector sum of the unit vector and the vector ![]() . Hence,
. Hence, ![]() is identical to the vector drawn from the point
is identical to the vector drawn from the point ![]() to the point in the vector
to the point in the vector ![]() as shown in Fig. 9.20.
as shown in Fig. 9.20.
Therefore, encirclement of the origin by the contour in ![]() -plane is similar to the encirclement of the point
-plane is similar to the encirclement of the point ![]() by the contour in
by the contour in ![]() -plane. Hence, the stability of the closed-loop system can be examined by determining the number of encirclements of
-plane. Hence, the stability of the closed-loop system can be examined by determining the number of encirclements of ![]() in
in ![]() -plane.
-plane.

Fig. 9.20 ∣ Relationship between ![]() -plane and
-plane and ![]() -plane
-plane
9.19 Nyquist Stability Criterion Based on the Encirclements of −1+ j 0
The Nyquist stability criterion based on the number of encirclements of ![]() is analyzed for two cases as below:
is analyzed for two cases as below:
Case 1: When the loop transfer function has no poles or zeros on the imaginary axis
If the loop transfer function of the system ![]() has
has ![]() number of poles in the right half of the
number of poles in the right half of the ![]() -plane, then for the system to be stable, the number of encirclements in the counterclockwise direction made by the locus in
-plane, then for the system to be stable, the number of encirclements in the counterclockwise direction made by the locus in ![]() plane around the point
plane around the point ![]() must be equal to
must be equal to ![]()
The above criterion can be expressed as
![]()
where ![]() is the number of zeros of
is the number of zeros of ![]() present in the right half of
present in the right half of ![]() -plane,
-plane, ![]() is the number of clockwise encirclements made by the locus of
is the number of clockwise encirclements made by the locus of ![]() around the point
around the point ![]() and
and ![]() is the number of poles of
is the number of poles of ![]() present in the right half of
present in the right half of ![]() -plane.
-plane.
Case 2: When the loop transfer function has poles and/or zeros on the imaginary axis
If the loop transfer function has poles and/or zeros on the imaginary axis, the Nyquist path is modified by drawing a small semicircle with very small radius ![]() as shown in Fig. 9.19(c).
as shown in Fig. 9.19(c).
If the loop transfer function of the system ![]() has
has ![]() number of poles in the right half of the
number of poles in the right half of the ![]() -plane, then for the system to be stable, the number of encirclements in the counterclockwise direction made by the modified locus in
-plane, then for the system to be stable, the number of encirclements in the counterclockwise direction made by the modified locus in ![]() -plane around the point
-plane around the point ![]() must be equal to
must be equal to ![]()
9.20 Stability Analysis of the System
Let ![]() be the number of zeros and
be the number of zeros and ![]() be the number of poles of the characteristic equation encircled by the
be the number of poles of the characteristic equation encircled by the ![]() -plane contour (Nyquist path), then the number of encirclements,
-plane contour (Nyquist path), then the number of encirclements, ![]() made by the
made by the ![]() -plane contour around the point
-plane contour around the point ![]() in the clockwise direction can be obtained as the difference between
in the clockwise direction can be obtained as the difference between ![]() and
and ![]()
i.e., ![]()
If ![]() is negative, it implies that the encirclement is in the counterclockwise direction. The different conditions for the system to be stable are discussed in Table 9.14.
is negative, it implies that the encirclement is in the counterclockwise direction. The different conditions for the system to be stable are discussed in Table 9.14.
Table 9.14 ∣ Conditions for the system to be stable

In general, the condition for the closed-loop stability is that ![]() must be equal to zero and the condition for the open-loop stability is that
must be equal to zero and the condition for the open-loop stability is that ![]() must be equal to zero.
must be equal to zero.
9.21 Procedure for Determining the Number of Encirclements
The procedure for determining the number of encirclements made by the contour in ![]() -plane around the point
-plane around the point ![]() is given below:
is given below:
Step 1: Construct the contour in ![]() -plane based on the Nyquist path in the
-plane based on the Nyquist path in the ![]() -plane.
-plane.
Step 2: Draw a dotted line from the point ![]() which is directed in the third quadrant of the
which is directed in the third quadrant of the ![]() -plane.
-plane.
Step 3: Chose any arbitrary point ![]() in the contour in the
in the contour in the ![]() -plane.
-plane.
Step 4: Starting from the point ![]() traverse the contour in the
traverse the contour in the ![]() -plane.
-plane.
Step 5: If the dotted line is cut by the contour in the clockwise direction, the number of encirclements ![]() is increased by one and if the dotted line is cut by the contour in the counterclockwise direction, the number of encirclements
is increased by one and if the dotted line is cut by the contour in the counterclockwise direction, the number of encirclements ![]() is decreased by one.
is decreased by one.
Step 6: Repeat the above step until the arbitrary point reaches the initial position.
Step 7: The value of ![]() present at the end of one complete rotation gives the number of encirclements made by the contour in
present at the end of one complete rotation gives the number of encirclements made by the contour in ![]() -plane around the point
-plane around the point ![]() .
.
The number of encirclements made by the different contours in ![]() -plane is listed in Table 9.15.
-plane is listed in Table 9.15.
Table 9.15 ∣ Number of encirclements for different contour in ![]() -plane
-plane

9.21.1 Flow chart for Determining the Number of Encirclements Made by the Contour in G(s)H(s)-Plane
The flow chart for determining the number of encirclements made by the contour in ![]() -plane is shown in Fig. 9.21.
-plane is shown in Fig. 9.21.

Fig. 9.21 ∣ Flow chart for number of encirclements
9.22 General Procedures for Determining the Stability of the System Based on Nyquist Stability Criterion
Step 1: Construct the Nyquist path that covers the whole right-hand side of the ![]() -plane based on the loop transfer function. The different Nyquist paths for different loop transfer functions are shown below:
-plane based on the loop transfer function. The different Nyquist paths for different loop transfer functions are shown below:
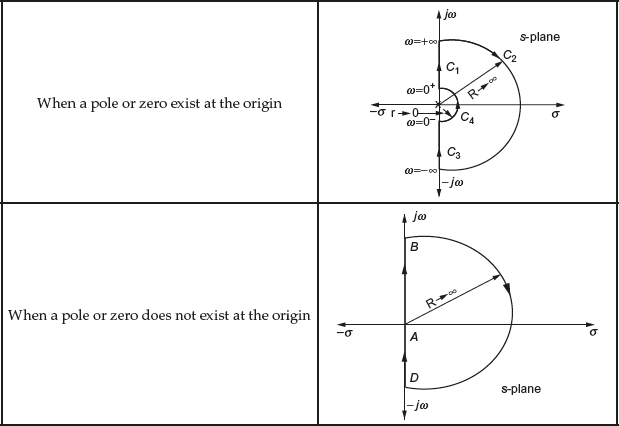
Step 2: Divide the Nyquist path into different sections with the value of ![]() and radius of the semi-circular path.
and radius of the semi-circular path.
Step 3: For each section present in the Nyquist path, determine the contour in the ![]() -plane.
-plane.
Step 4: The intersection point of the contour on the real axis is determined by substituting ![]() at which the imaginary part of the transfer function is zero.
at which the imaginary part of the transfer function is zero.
Step 5: Complete the contour in the ![]() -plane for the given system by joining the individual contours determined in the previous step.
-plane for the given system by joining the individual contours determined in the previous step.
Step 6: Determine the number of encirclements ![]() made by the contour in
made by the contour in ![]() -plane around the point
-plane around the point ![]() .
.
Step 7: For the given loop transfer function, determine the number of poles ![]() existing in the right half of the
existing in the right half of the ![]() -plane.
-plane.
Step 8: Determine the number of zeros, ![]() existing in the right half of the
existing in the right half of the ![]() -plane by using
-plane by using ![]() .
.
Step 9: Using Table 9.15, examine the closed-loop stability of the system.
9.22.1 Flow chart for Determining the Stability of the System Based on Nyquist Stability Criterion
The flow chart for determining the stability of the system based on Nyquist stability criterion is shown in Fig. 9.22.

Fig. 9.22 ∣ Flow chart for examining the stability of the system
Example 9.6: The loop transfer function of a certain control system is given by ![]() . Sketch the Nyquist plot and hence calculate the range of values of K for stability.
. Sketch the Nyquist plot and hence calculate the range of values of K for stability.
Solution:
- In general, the Nyquist path for a system is considered to have a complete right-hand side of the
 -plane covering the entire imaginary axis including the origin. In addition, the Nyquist path should not pass through any poles and/or zeros on the imaginary axis.
-plane covering the entire imaginary axis including the origin. In addition, the Nyquist path should not pass through any poles and/or zeros on the imaginary axis.
As the pole at the origin for the given system exists, a small semicircle with infinitesimal radius is drawn around the origin of the Nyquist path. The modified Nyquist path for the system is shown in Fig. E9.6(a).

Fig. E9.6(a)
- The different sections present in Fig. E9.6(a) alongwith its parameters are listed in Table E9.6(a).
Table E9.6(a) ∣ Sections present in the Nyquist path

- Construct a contour in
 -plane for each section given in Table E9.6(a) and the individual contours are listed in Table E9.6(b).
-plane for each section given in Table E9.6(a) and the individual contours are listed in Table E9.6(b).
Table E9.6(b) ∣ Contours for different sections

- To determine the intersection point of the contour in the real axis:
The loop transfer function of the given system is

Therefore,



Hence, the real part of the transfer function =

and the imaginary part of the transfer function =

Equating the imaginary part of the above transfer function to zero, we obtain

 or
or 
Substituting
 in the real part of the transfer function, we obtain the intersection point
in the real part of the transfer function, we obtain the intersection point  as
as  .
. - The individual contours obtained in step (iii) are combined together to construct the complete contour in
 -plane alongwith the intersection point as shown in Fig. E9.6(b).
-plane alongwith the intersection point as shown in Fig. E9.6(b).
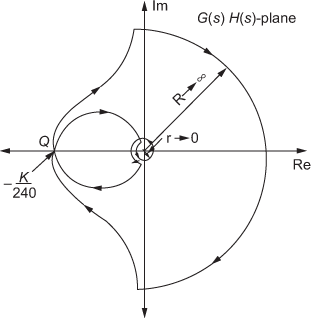
Fig. E9.6(b)
- The number of encirclements made by the contour in
 -plane around the point
-plane around the point  for the given system cannot be determined as the intersection point depends on the gain
for the given system cannot be determined as the intersection point depends on the gain  .
. - For the given system, the number of poles which lies in the right half of the
 -plane is zero, i.e.,
-plane is zero, i.e.,  .
. - The number of zeros which lies in the right half of the
 -plane cannot be determined for the given system.
-plane cannot be determined for the given system. - Hence, the stability of the system depends on the gain
 .
. - To determine the range of gain
 for the system to be stable:
for the system to be stable:
For the system to be stable,
 should be less than −1
should be less than −1i.e.,
 or
or 
Therefore, for the system to be stable, the range of gain
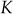 is
is  .
.
Example 9.7: The loop transfer function of a certain control system is given by ![]() . Sketch the Nyquist plot and comment on the stability of the system.
. Sketch the Nyquist plot and comment on the stability of the system.
Solution:
- As there exists no pole on the imaginary axis for the given system, the Nyquist path for the original system is shown in Fig. E9.7(a).

Fig. E9.7(a)
- The different sections present in Fig. E9.7(a) alongwith parameters are listed in Table E9.7(a).
Table E9.7(a) ∣ Sections present in the Nyquist path

- Construct a contour in
 -plane for each section given in Table E9.7(a) and the individual contours are listed in Table E9.7(b).
-plane for each section given in Table E9.7(a) and the individual contours are listed in Table E9.7(b).
Table E9.7(b) ∣ Contours for different sections

- To determine the intersection point of the complete contour in the real axis:
The loop transfer function of the given system is

Therefore,

=



Hence, the real part of the transfer function =
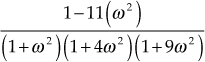
and the imaginary part of the transfer function =

Equating the imaginary part of the transfer function to zero, we obtain

 or
or  .
.Substituting
 in the real part of the transfer function, we obtain the intersection point
in the real part of the transfer function, we obtain the intersection point  as
as
- The individual contours obtained in step (iii) are combined together to construct the complete contour in
 -plane alongwith the intersection point as shown in Fig. E9.7(b).
-plane alongwith the intersection point as shown in Fig. E9.7(b).

Fig. E9.7(b)
- The number of encirclements made by the contour in
 -plane around the point
-plane around the point  for the given system is 0, i.e.,
for the given system is 0, i.e.,  .
. - For the given system, the number of poles which lies in the right half of the
 -plane is zero, i.e.,
-plane is zero, i.e.,  .
. - The number of zeros which lies in the right half of the
 -plane is determined by using
-plane is determined by using  .
. - Using Table 9.15 and the value of
 obtained in the previous step, we may conclude that the system is stable.
obtained in the previous step, we may conclude that the system is stable.
Example 9.8: The loop transfer function of a certain control system is given by ![]() . Sketch the Nyquist plot and comment on the stability of the system.
. Sketch the Nyquist plot and comment on the stability of the system.
Solution:
- As two poles exist at the origin for the given system, the Nyquist path for the system is shown in Fig. E9.8(a).

Fig. E9.8(a)
- The different sections present in Fig. E9.8(a) alongwith its parameters are listed in Table E9.8(a).
Table E9.8(a) ∣ Sections present in the Nyquist path

- Construct a contour in
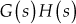 -plane for each section given in Table E9.8(a) and the individual contours are listed in Table E9.8(b).
-plane for each section given in Table E9.8(a) and the individual contours are listed in Table E9.8(b).
Table E9.8(b) ∣ Contours for different sections

- To determine the intersection point of the complete contour in the real axis:
The loop transfer function of the given system is

Therefore,

=


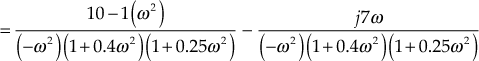
Hence, the real part of the transfer function =

and the imaginary part of the transfer function =
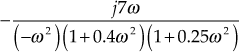
Equating the imaginary part of the transfer function to zero, we obtain
 .
.Substituting
 in the real part of the transfer function, we obtain the intersection point
in the real part of the transfer function, we obtain the intersection point  . Hence, there is no valid intersection point of contour on the imaginary axis.
. Hence, there is no valid intersection point of contour on the imaginary axis. - The individual contours obtained in step (iii) are combined together to construct the complete contour in
 -plane as shown in Fig. E9.8(b).
-plane as shown in Fig. E9.8(b).
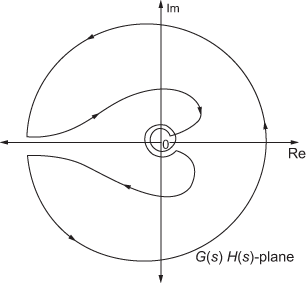
Fig. E9.8(b)
- The number of encirclements made by the contour in
 -plane around the point
-plane around the point  for the given system is 2, i.e.,
for the given system is 2, i.e.,  .
. - For the given system, the number of poles which lies in the right half of the
 -plane is 0, i.e.,
-plane is 0, i.e.,  .
. - The number of zeros which lies in the right half of the
 -plane is determined by using
-plane is determined by using  .
. - Using the Table 9.15 and the value of
 obtained in the previous step, we may conclude that the system is unstable.
obtained in the previous step, we may conclude that the system is unstable.
Example 9.9: The loop transfer function of a certain control system is given by ![]() . Sketch the Nyquist plot and examine the stability of the system.
. Sketch the Nyquist plot and examine the stability of the system.
Solution:
- As no pole exists at the origin for the given system, the Nyquist path for the system is shown in Fig. E9.9(a).
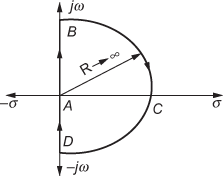
Fig. E9.9(a)
- The different sections present in Fig. E9.9(a) alongwith its parameters are listed in Table E9.9(a).
Table E9.9(a) ∣ Sections present in the Nyquist path

- Construct a contour in
 -plane for each section given in Table E9.9(a) and the individual contours are listed in Table E9.9(b).
-plane for each section given in Table E9.9(a) and the individual contours are listed in Table E9.9(b).
Table E9.9(b) ∣ Contours for different sections

- To determine the intersection point of the contour in the real axis:
The loop transfer function of the given system is

Therefore,


Hence, the real part of the transfer function =

and the imaginary part of the transfer function =
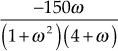
Equating the imaginary part of the above transfer function to zero, we obtain

Substituting
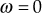 in the real part of the transfer function, we obtain the intersection point
in the real part of the transfer function, we obtain the intersection point  as
as  . Hence, other than the point
. Hence, other than the point  , we have no intersection of the contour in the
, we have no intersection of the contour in the  -plane.
-plane. - The individual contours obtained in step (iii) are combined together to construct the complete contour in
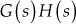 -plane alongwith the intersection point as shown in Fig. E9.9(b).
-plane alongwith the intersection point as shown in Fig. E9.9(b).

Fig. E9.9(b)
- The number of encirclements made by the contour in
 -plane around the point
-plane around the point  for the given system is zero, i.e.,
for the given system is zero, i.e., 
- For the given system, the number of poles which lies in the right half of the
 -plane is zero, i.e.,
-plane is zero, i.e.,  .
. - The number of zeros which lies in the right half of the
 -plane is
-plane is  .
. - As the value of zero which lies in the right half of the
 -plane is zero, the system is stable.
-plane is zero, the system is stable.
Example 9.10: The loop transfer function of a certain control system is given by ![]() . Sketch the Nyquist plot and examine the stability of the system.
. Sketch the Nyquist plot and examine the stability of the system.
Solution:
- As no pole exists at the origin for the given system, the Nyquist path for the system is shown in Fig. E9.10(a).

Fig. E9.10(a)
- The different sections present in Fig. E9.10(a) alongwith its parameters are listed in Table E9.10(a).
Table E9.10(a) Sections present in the Nyquist path

- Construct a contour in
 -plane for each section given in Table E9.10(a) and the individual contours are listed in Table E9.10(b).
-plane for each section given in Table E9.10(a) and the individual contours are listed in Table E9.10(b).
Table E9.10(b) Contours for different sections

- To determine the intersection point of the contour in the real axis:
The loop transfer function of the given system is

Therefore,


Hence, the real part of the transfer function =

and the imaginary part of the transfer function =

Equating the imaginary part of the above transfer function to zero, we obtain
 .
.Substituting
 in the real part of the transfer function, we obtain the intersection point
in the real part of the transfer function, we obtain the intersection point  as
as  . Therefore, the contour crosses the real axis only at
. Therefore, the contour crosses the real axis only at  .
. - The individual contours obtained in step (iii) are combined together to construct the complete contour in
 -plane alongwith the intersection point as shown in Fig. E9.10(b).
-plane alongwith the intersection point as shown in Fig. E9.10(b). - The number of encirclements made by the contour in
 -plane around the point
-plane around the point 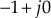 for the given system is zero, i.e.,
for the given system is zero, i.e.,  .
. - For the given system, the number of poles which lies in the right half of the
 -plane is zero, i.e.,
-plane is zero, i.e.,  .
. - The number of zeros which lies in the right half of the
 -plane is
-plane is  .
. - As the value of zero which lies in the right half of the
 -plane is zero, the system is stable.
-plane is zero, the system is stable.
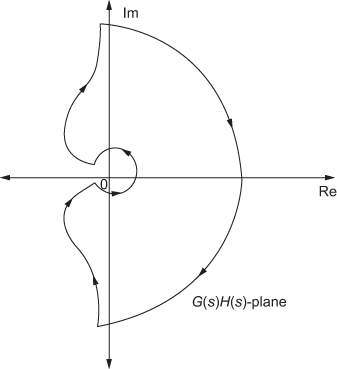
Fig. E9.10(b)
Example 9.11: The loop transfer function of a certain control system is given by ![]() . Sketch the Nyquist plot and examine the stability of the system.
. Sketch the Nyquist plot and examine the stability of the system.
Solution:
- As two poles exist at the origin for the given system, the Nyquist path for the system is shown in Fig. E9.11(a).

Fig. E9.11(a)
- The different sections present in Fig. E9.11(a) alongwith its parameters are listed in Table E9.11(a).
Table E9.11(a) ∣ Sections present in the Nyquist path

- Construct a contour in
 -plane for each section given in Table E9.11(a) and the individual contours are listed in Table E9.11(b).
-plane for each section given in Table E9.11(a) and the individual contours are listed in Table E9.11(b).
Table E9.11(b) ∣ Contours for different sections

- To determine the intersection point of the contour in the real axis:
The loop transfer function of the given system is

We know that when the
 contour crosses the real axis, the phase angle of the system will be
contour crosses the real axis, the phase angle of the system will be  .
.Hence,
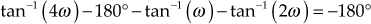

Taking
 on both sides of the equation, we obtain
on both sides of the equation, we obtain
We know that,

Using the above equation, we obtain
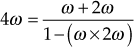
Upon solving, we obtain
 rad/sec
rad/secSubstituting
 in the magnitude of the transfer function, we obtain
in the magnitude of the transfer function, we obtain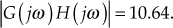
Therefore, the contour intersects the real axis at

- The individual contours obtained in step (iii) are combined together to construct the complete contour in
 -plane alongwith the intersection point as shown in Fig. E9.11(b).
-plane alongwith the intersection point as shown in Fig. E9.11(b).

Fig. E9.11(b)
- The number of encirclements made by the contour in
 -plane around the point
-plane around the point  for the given system is zero, i.e.,
for the given system is zero, i.e.,  .
. - For the given system, the number of poles which lies in the right half of the
 -plane is zero, i.e.,
-plane is zero, i.e.,  .
. - The number of zeros which lies in the right half of the
 -plane is
-plane is  .
. - As the value of zero which lies in the right half of the
 -plane is zero, the system is unstable.
-plane is zero, the system is unstable.
Example 9.12: The loop transfer function of a certain control system is given by  . Sketch the Nyquist plot and examine the stabilityof the system.
. Sketch the Nyquist plot and examine the stabilityof the system.
Solution:
- As three poles exist at the origin for the given system, the Nyquist path for the system is shown in Fig. E9.12(a).

Fig. E9.12(a)
- The different sections present in Fig. E9.12(a) alongwith its parameters are listed in Table E9.12(a).
Table E9.12(a) ∣ Sections present in the Nyquist path

- Construct a contour in
 -plane for each section given in Table E9.12(a) and the individual contours are listed in Table E9.12(b).
-plane for each section given in Table E9.12(a) and the individual contours are listed in Table E9.12(b).
Table E9.12(b) ∣ Contours for different sections

- To determine the intersection point of the contour in the real axis:
The loop transfer function of the given system is

Therefore,

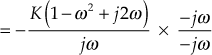

Hence, the real part of the transfer function =
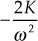
and the imaginary part of the transfer function =
 .
.Equating the imaginary part of the transfer function, we obtain

Substituting
 in the real part of the transfer function, we obtain the intersection point Q as
in the real part of the transfer function, we obtain the intersection point Q as  .
. - The individual contours obtained in step (iii) are combined together to construct the complete contour in
 -plane alongwith the intersection point as shown in Fig. E9.12(b).
-plane alongwith the intersection point as shown in Fig. E9.12(b).

Fig. E9.12(b)
- The number of encirclements made by the contour in
 -plane around the point
-plane around the point 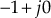 for the given system cannot be determined as the intersection point depends on the gain
for the given system cannot be determined as the intersection point depends on the gain  .
. - For the given system, the number of poles which lies in the right half of the
 -plane is zero, i.e.,
-plane is zero, i.e.,  .
. - The number of zeros which lies in the right half of the
 -plane cannot be determined for the given system.
-plane cannot be determined for the given system. - As the value of zero which lies in the right half of the
 -plane is not determined, the stability of the system cannot be analyzed. The stability of the system depends on the
-plane is not determined, the stability of the system cannot be analyzed. The stability of the system depends on the  .
. - To determine the range of gain
 for the system to be stable:
for the system to be stable:
For the system to be stable,
 should be less than −1.
should be less than −1.i.e.,
 or
or 
Therefore, for the system to be stable, the range of gain
 is
is  .
.
Example 9.13: The loop transfer function of a certain control system is given by  . Sketch the Nyquist plot and examine the stability of the system.
. Sketch the Nyquist plot and examine the stability of the system.
Solution:
- As no poles exist at the origin for the given system, the Nyquist path for the system is shown in Fig. E9.13(a).

Fig. E9.13(a)
- The different sections present in Fig. E9.13(a) alongwith parameters are listed in Table E9.13(a).
Table E9.13(a) ∣ Sections present in the Nyquist path

- Construct a contour in
 -plane for each section given in Table E9.13(a) and the individual contour is listed in Table E9.13(b).
-plane for each section given in Table E9.13(a) and the individual contour is listed in Table E9.13(b).
Table E9.13(b) ∣ Contour for different sections

- To determine the intersection point of the contour in the real axis:
The loop transfer function of the given system is

Therefore,

Hence, the real part of the transfer function =

and the imaginary part of the transfer function =
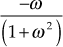 .
.Equating the imaginary part of the transfer function, we obtain
 .
.As the real part of the transfer function is independent of
 , there is no intersection point on the real axis other than −2.
, there is no intersection point on the real axis other than −2. - (v) The individual contours obtained in step (iii) are combined together to construct the complete contour in
 -plane alongwith the intersection point as shown in Fig. E9.13(b).
-plane alongwith the intersection point as shown in Fig. E9.13(b). - The number of encirclements made by the contour in
 -plane around the point
-plane around the point  for the given system is
for the given system is  .
. - For the given system, the number of poles which lies in the right half of the
 -plane is zero, i.e.,
-plane is zero, i.e.,  .
. - The number of zeros which lies in the right half of the
 -plane for the given system is
-plane for the given system is  .
. - As the value of zero which lies in the right half of the
 -plane is zero the given system is stable.
-plane is zero the given system is stable.

Fig. E9.13(b)
Review Questions
- A feedback control system is characterized by the open-loop transfer function

- Draw the polar plot of the open-loop system. Calculate the magnitude and phase at 10 equi-spaced frequency points, including the point where the plot intersects the imaginary axis and use them to construct the plot.
- From the polar plot, how will you determine the gain margin, phase margin, gain crossover frequency and phase crossover frequency? Comment on the system stability.
- Draw the polar plot of each of the following complex functions:
-
- Sketch the polar plot for
 ,
,  .
. - Determine: (a) the phase crossover frequency, (b) the gain crossover frequency, (c) the gain margin and (d) phase margin for the system of
 with
with  and
and 
- Sketch the polar plot for
- Sketch the polar plot for the following loop transfer function (a)
 and (b)
and (b)  .
. - Draw the polar plot for the unity feedback system given by
 and determine the range of for the stability of the system.
and determine the range of for the stability of the system. - Sketch the polar plot for the unity feedback system given by
 and find the phase margin.
and find the phase margin. - Draw the polar plot for the transfer function of a system
 .
. - Consider the transfer function
 Draw the polar plot for
Draw the polar plot for 
- Consider the non-minimum phase transfer function
 Sketch the polar plot.
Sketch the polar plot. - Draw the polar plot for the transfer function

- Consider the following transfer function
 Show that the polar plot of
Show that the polar plot of  in the
in the  plane is a circle
plane is a circle  and diameter
and diameter  as
as  varies from
varies from  to
to  .
. - Determine graphically the gain margin and phase margin and gain and phase crossover frequencies for the system whose open-loop transfer function is given as
 .
. - The open-loop transfer function of a unity feedback control system is given by
 . Sketch the polar plot and determine the gain margin and phase margin.
. Sketch the polar plot and determine the gain margin and phase margin. - Determine the phase margin ad gain margin for the system whose transfer function is
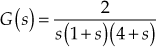 . Use polar plot.
. Use polar plot. - The open-loop transfer function of a unity feedback control system is given by
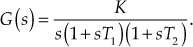 Derive an expression for the gain
Derive an expression for the gain  in terms of
in terms of  and
and  and specify the gain margin
and specify the gain margin 
- Draw the polar plot for the following transfer functions (a)
 and (b)
and (b) 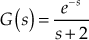 .
. - For the following transfer function draw the actual polar plot by calculating the magnitude and phase for

- Determine analytically phase margin, gain margin, phase crossover frequency and gain-crossover frequency for the transfer function given below. Draw the polar plot.

- Sketch the polar plot for the following transfer function:

- For an RLC series network, the output is taken across the capacitor. The transfer function is
 where the undamped natural frequency
where the undamped natural frequency  and damping coefficient
and damping coefficient  . Draw the polar plot.
. Draw the polar plot. - Obtain the polar plot for the unity feedback control system having open-loop transfer function as
 , assume
, assume  .
. - State and explain the Nyquist criterion for stability.
- State the Nyquist stability criterion for the stability of a closed-loop system and compare it with Routh's criterion.
- Given the open-loop transfer function
 , determine the condition of stability from the polar plot. Verify this condition using Routh–Hurwitz criterion.
, determine the condition of stability from the polar plot. Verify this condition using Routh–Hurwitz criterion. - Write a note on Nyquist path.
- Define gain margin and phase margin with reference to Nyquist plot.
- Explain clearly with the necessary mathematical preliminaries the Nyquist criterion for stability.
- Explain the conditionally stable system. With the help of a Nyquist plot, show the behaviour of such systems.
- What are the effects of additional poles and zeros on the shape of the Nyquist loci? Explain using appropriate diagrams.
- Define principle of arguments.
- Using Nyquist criterion, investigate the stability of the system
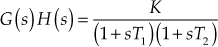
- If a position control system has the forward loop transfer function
 , determine the gain margin and phase margin the system using Nyquist plot.
, determine the gain margin and phase margin the system using Nyquist plot. - Given
 , determine the stability range of K using Nyquist's stability criterion.
, determine the stability range of K using Nyquist's stability criterion. - The loop transfer function of a unity feedback system is given by
 . Sketch the polar plot for the system and determine the gain and phase margin of the system.
. Sketch the polar plot for the system and determine the gain and phase margin of the system. - The loop transfer function of a unity feedback system is given by
 . Sketch the polar plot for the system and determine the gain and phase margin of the system.
. Sketch the polar plot for the system and determine the gain and phase margin of the system. - The loop transfer function of a unity feedback system is given by
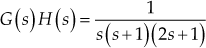 . Sketch the polar plot for the system.
. Sketch the polar plot for the system. - The open-loop transfer function of a feedback system is
 , determine its stability using Nyquist criterion.
, determine its stability using Nyquist criterion. - Sketch the Nyquist plot for
 and determine whether the closed-loop system is stable or not.
and determine whether the closed-loop system is stable or not. - The loop transfer function is
 Determine, using Nyquist stability criterion, the critical value of K for stability of closed-loop system.
Determine, using Nyquist stability criterion, the critical value of K for stability of closed-loop system. - A position control system has the forward loop transfer function
 . Draw the Nyquist plot and determine the stability of the closed-loop system.
. Draw the Nyquist plot and determine the stability of the closed-loop system. - Sketch the Nyquist plot for the system whose open-loop transfer function is given by
 and using Nyquist stability criterion, check whether system is stable.
and using Nyquist stability criterion, check whether system is stable. - The open-loop transfer function of a unity feedback control system is given by
 . Draw the Nyquist plot and calculate the gain margin.
. Draw the Nyquist plot and calculate the gain margin. - The loop transfer function of a feedback system is given by
 . Sketch the Nyquist plot and determine the stability and hence the gain and phase margins.
. Sketch the Nyquist plot and determine the stability and hence the gain and phase margins. - Sketch the Nyquist plot for the following open-loop transfer function and comment on the stability
 . Determine the gain and phase margins.
. Determine the gain and phase margins. - A control system has the loop transfer function
 . Sketch the Nyquist diagram and determine its stability.
. Sketch the Nyquist diagram and determine its stability. - The loop transfer function of a feedback system is
 . Using Nyquist method, determine the stability of the system.
. Using Nyquist method, determine the stability of the system.





