CHAPTER 13
Priority Queues
In this chapter, we examine the priority queue data type. A priority queue is a collection in which only the element with highest priority can be removed, according to some method for comparing elements. This restriction allows an implementation—the Java Collections Framework's PriorityQueue class—with an add method whose average time is constant. The PriorityQueue class can be enhanced by including heapSort, a fast sort method for which worstSpace(n) is constant. The chapter concludes by using a priority queue to generate a Huffman Tree—a necessary component of a popular data-compression technique called Huffman compression.
CHAPTER OBJECTIVES
- Understand the defining property of a priority queue, and how the Java Collections Framework's PriorityQueue class violates that property.
- Be able to perform the heap operations of siftUp and siftDown.
- Compare Heap Sort to Merge Sort with respect to time and space requirements.
- Examine the Huffman data-compression algorithm.
- Determine the characteristic of a greedy algorithm.
13.1 Introduction
A variation of the queue, the priority queue is a commonplace structure. The basic idea is that we have elements waiting in line for service, as with a queue. But removals are not strictly on a first-in-first-out basis. For example, patients in an emergency room are treated according to the severity of their injuries, not according to when they arrived. Similarly, in air-traffic control, when there is a queue of planes waiting to land, the controller can move a plane to the front of the queue if the plane is low on fuel or has a sick passenger.
A shared printer in a network is another example of a resource suited for a priority queue. Normally, jobs are printed based on arrival time, but while one job is printing, several others may enter the service queue. Highest priority could be given to the job with the fewest pages to print. This would optimize the average time for job completion. The same idea of prioritized service can be applied to any shared resource: a central processing unit, a family car, the courses offered next semester, and so on.
Here is the definition:
A priority queue is collection in which removal is of the highest-priority element in the collection, according to some method for comparing elements.
For example, if the elements are of type (reference to) Integer and comparisons use the "natural" ordering, then the highest-priority element is the one whose corresponding int has the smallest value in the priority queue. But if elements are of type Integer and the comparisons use the reverse of the natural ordering, then the highest-priority element is the one whose corresponding int has the largest value in the priority queue. By default, the smallest-valued element has highest priority.
This definition says nothing about insertions. In the PriorityQueue class, the method add (E element) takes only constant time on average, but linear-in-n time in the worst case. What underlying structure do these times suggest?
You might wonder what happens if two or more elements are tied for highest priority. In the interest of fairness, the tie should be broken in favor of the element that has been in the priority queue for the longest time. This appeal to fairness is not part of the definition, and is not incorporated into the PriorityQueue class. Lab 21 provides a solution to this problem.
Most of this chapter is devoted to an important application of priority queues: Huffman encoding. Also, Chapter 15 has two widely used priority-queue applications: Prim's minimum-spanning-tree algorithm and Dijkstra's shortest-path algorithm. For a lively discussion of the versatility of priority queues, see Dale [1990].
13.2 The PriorityQueue Class
The PriorityQueue class, which complements the Queue interface, is in the package java.util. That fact has the significant benefit that the PriorityQueue class is available to you whenever you program in Java. But the PriorityQueue class also has a flaw: It allows methods—such as remove (Object obj)—that violate the definition of a priority queue. If you want a PurePriorityQueue class, you have the same two choices as were available for the PureStack and PureQueue classes in Chapter 8. You can extend the PriorityQueue class to a PurePriorityQueue class that throws Unsupported OperationException for the removal of any element except the highest-priority element. Or you can create a minimalist PurePriorityQueue class that allows only a few methods: a couple of constructors, isEmpty(), size(), add (E element), remove(), and element().
The PriorityQueue class has some unusual features. For example, null values are not permitted. Why? Because some removal methods, such as poll(), and some access methods (such as peek()) return null if the priority queue is empty. If null values were allowed, there would be ambiguity if poll() returned null: That value could signify an empty queue, or could simply be the value of the highest priority element.
The creator of a PriorityQueue object can order the elements "naturally" (with the element class's Comparable interface) or else provide a Comparator class for comparisons.
Here are the specifications for two constructors and three other essential methods:
/** * Initializes a PriorityQueue object with the default initial capacity (11) that orders its * elements according to their natural ordering (using Comparable). */ public PriorityQueue() /** * Initializes a PriorityQueue object with the specified initial capacity * that orders its elements according to the specified comparator. * * @param initialCapacity the initial capacity for this priority queue. * @param comparator the comparator used to order this priority queue. * If null then the order depends on the elements' natural ordering. * @throws IllegalArgumentException if initialCapacity is less than 1 */ public PriorityQueue(int initialCapacity, Comparator<? super E> comparator) /** * Inserts a specified element into this PriorityQueue object. * The worstTime(n) is O(n) and averageTime(n) is constant. * * @param element -the element to be inserted into this PriorityQueue object. * @return true * @throws NullPointerException -if element is null. * @throws ClassCastException if the specified element cannot be compared * with elements currently in the priority queue according * to the priority queue's ordering. * */ public boolean add (E element) /** * Retrieves and removes the highest priority element of this PriorityQueue object. * The worstTime(n) is O(log n). * * @return the highest priority element of this PriorityQueue object. * @throws NoSuchElementException if this queue is empty. */ public E remove() /** * Retrieves, but does not remove, the highest priority element of this PriorityQueue * object. * The worstTime(n) is constant. * * @return the highest priority element of this PriorityQueue object. * @throws NoSuchElementException if this queue is empty. */ public E element()
13.3 Implementation Details of the PriorityQueue Class
In any instance of the PriorityQueue class, the elements are stored in a heap. A heap t is a complete binary tree such that either t is empty or
- the root element is the smallest element in t, according to some method for comparing elements;
- the left and right subtrees of t are heaps.
(The heap we have defined is called a "minHeap". In a "maxHeap", the root element is the largest element.)
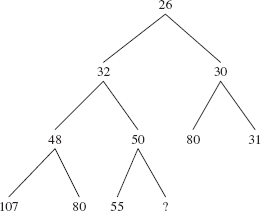
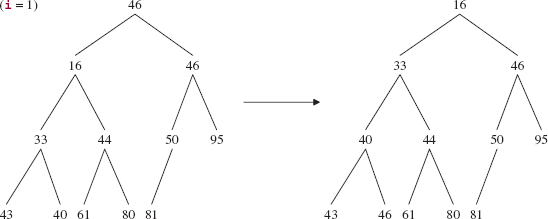
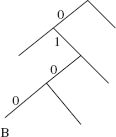
Recall from Chapter 9 that a complete binary tree is full except, possibly, at the level farthest from the root, and at that farthest level, the leaves are as far to the left as possible. Figure 13.1 shows a heap of ten Integer elements with the "natural" ordering. Notice that a heap is not a binary search tree. For example, duplicates are allowed in a heap, unlike the prohibition against duplicates for binary search trees.
FIGURE 13.1 A heap with ten (reference to) Integer elements; the int values of the Integer elements are shown
The ordering in a heap is top-down, but not left-to-right: the root element of each subtree is less than or equal to each of its children, but some left siblings may be less than their right siblings and some may be greater than or equal to. In Figure 13.1, for example, 48 is less than its right sibling, 50, but 107 is greater than its right sibling, 80. Can you find an element that is smaller than its parent's sibling?
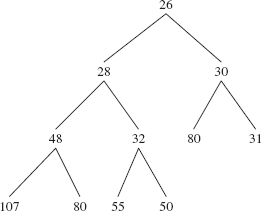
A heap is a complete binary tree. We saw in Chapter 9 that a complete binary tree can be implemented with an array. Figure 13.2 shows the array version of Figure 13.1, with each index under its element. An iteration over a PriorityQueue object uses the index-ordering of the array, so the iteration would be 26, 32, 30, 48, 50, 80, 31, 107, 80, 55.
Recall from Chapter 9 that the random-access feature of arrays is convenient for processing a complete binary tree: Given the index of an element, that element's children can be accessed in constant time. For example, with the array as shown in Figure 13.2, the children of the element at index i are at indexes (i << 1) + 1 and (i << 1) + 2. And the parent of the element at index j is at index (j - 1) >> 1.
FIGURE 13.2 The array representation of the heap from Figure 13.1

As we will see shortly, the ability to quickly swap the values of a parent and its smaller-valued child makes a heap an efficient storage structure for the PriorityQueue class.
Here is program that creates and maintains two PriorityQueue objects in which the elements are of type Student, declared below. Each line of input—except for the sentinel—consists of a name and the corresponding grade point average (GPA). The highest-priority student is the one whose GPA is lowest. In the Student class, the Comparable interface is implemented by specifying increasing order of grade point averages. To order another heap by alphabetical order of student names, a ByName comparator class is defined.
import java.util.*; public class PriorityQueueExample { public static void main (String[ ] args) { new PriorityQueueExample().run(); } // method main public void run() { final int DEFAULT_INITIAL_CAPACITY = 11; final String PROMPT1 = "Please enter student's name and GPA, or " ; final String PROMPT2 = " to quit: "; final String SENTINEL = "***"; final String RESULTS1 = " Here are the student names and GPAs, " + "in increasing order of GPAs:"; final String RESULTS2 = " Here are the student names and GPAs, " + "in alphabetical order of names:"; PriorityQueue<Student> pq1 = new PriorityQueue<Student>(), pq2 = new PriorityQueue<Student> (DEFAULT_INITIAL_CAPACITY, new ByName()); Scanner sc = new Scanner (System.in); String line; while (true) { System.out.print (PROMPT1 + SENTINEL + PROMPT2); line = sc.nextLine(); if (line.equals (SENTINEL)) break; pq1.add (new Student (line)); pq2.add (new Student (line)); } // while System.out.println (RESULTS1); while (!pq1.isEmpty()) System.out.println (pq1.remove()); System.out.println (RESULTS2); while (!pq2.isEmpty()) System.out.println (pq2.remove()); } // method run } // class PriorityQueueExample // in another file import java.util.*; public class Student implements Comparable<Student> { protected String name; protected double gpa; /** * Initializes this Student object from a specified String object. * * @param s - the String object used to initialize this Student object. * */ public Student (String s) { Scanner sc = new Scanner (s); name = sc.next(); gpa = sc.nextDouble(); } // constructor /** * Compares this Student object to a specified Student object by * grade point average. * * @param otherStudent - the specified Student object. * * @return a negative integer, 0, or a positive integer, depending * on whether this Student object's grade point average is less than, * equal to, or greater than otherStudent's grade point average. * */ public int compareTo (Student otherStudent) { if (gpa < otherStudent.gpa) return -1; if (gpa > otherStudent.gpa) return 1; return 0; } // method compareTo /** * Returns a String representation of this Student object. * * @return a String representation of this Student object: name " " gpa * */ public String toString() { return name + " " + gpa; } // method toString } // class Student // in another file: import java.util.*; public class ByName implements Comparator<Student> { public int compare (Student stu1, Student stu2) { String name1 = new Scanner (stu1.toString()).next(), name2 = new Scanner (stu2.toString()).next(); return name1.compareTo (name2); } // method compare } // class ByName
The Student class implements the Comparable interface with a compareTo method that returns −1, 0, or 1, depending on whether the calling Student object's grade point average is less than, equal to, or greater than another student's grade point average. So, as you would expect, the Student with the lowest grade point average is the highest-priority element. Suppose the input for the PriorityQueueExample program is as follows:
Soumya 3.4 Navdeep 3.5 Viet 3.5 ***
Here is the output of the students as they are removed from pq1:
Soumya 3.4 Viet 3.5 Navdeep 3.5
Notice that Viet is printed before Navdeep even though they have the same grade point average, and Navdeep was input earlier than Viet. As mentioned earlier, the PriorityQueue class—like life—is unfair. In Section 13.3.1, we look at more details of the PriorityQueue class, which will help to explain how this unfairness comes about. Lab 21 will show you how to remedy the problem.
For pq2 in the PriorityQueueExample program above, the output of students would be
Navdeep 3.5 Soumya 3.4 Viet 3.5
13.3.1 Fields and Method Definitions in the PriorityQueue Class
The critical field in the PriorityQueue class will hold the elements:
private transient Object[ ] queue;
And—similar to the TreeMap class—we also have size, comparator, and modCount fields:
/** * The number of elements in the priority queue. */ private int size = 0; /** * The comparator, or null if priority queue uses elements' * natural ordering. */ private final Comparator<? super E> comparator; /** * The number of times this priority queue has been * structurally modified. See AbstractList class and Appendix 1 for gory details. */ private transient int modCount = 0;
The following constructor definition creates a priority queue with a specified initial capacity and an ordering supplied by a specified comparator:
/** * Initializes a PriorityQueue object with the specified initial capacity * that orders its elements according to the specified comparator. * * @param initialCapacity the initial capacity for this priority queue. * @param comparator the comparator used to order this priority queue. * If null then the order depends on the elements' natural ordering. * @throws IllegalArgumentException if initialCapacity is less than 1 */ public PriorityQueue (int initialCapacity, Comparator<? super E> comparator) { if (initialCapacity < 1) throw new IllegalArgumentException(); queue = new Object[initialCapacity]; this.comparator = comparator; } // constructor
The definition of the default constructor follows easily:
/** * Initializes a PriorityQueue object with the default initial capacity (11) * that orders its elements according to their natural ordering (using Comparable). */ public PriorityQueue( ) { this (DEFAULT_INITIAL_CAPACITY, null); } // default constructor
Now let's define the add (E element), element(), and remove() methods. The add (E element) method expands that array if it is full, and calls an auxiliary method, siftUp, to insert the element and restore the heap property. Here are the specifications and definition:
/** * Inserts the specified element into this priority queue. * The worstTime(n) is O(n) and averageTime(n) is constant. * * @return {@code true} (as specified by {@link Collection#add}) * @throws ClassCastException if the specified element cannot be * compared with elements currently in this priority queue * according to the priority queue's ordering * @throws NullPointerException if the specified element is null */ public boolean add(E e) { if (e == null) throw new NullPointerException(); modCount++; int i = size; if (i >= queue.length) grow(i + 1); size = i + 1; if (i == 0) queue[0] = e; else siftUp(i, e); return true; }
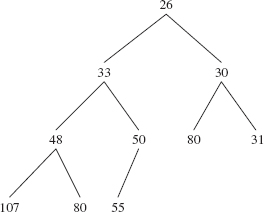
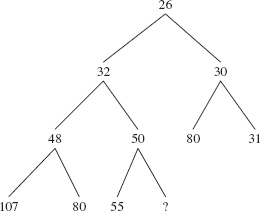
For example, Figure 13.3 shows what the heap in Figure 13.1 will look like just before siftUp (10, new Integer (28)) is called.
FIGURE 13.3 The heap from Figure 13.1 just before 28 is inserted. The size is 10.
13.3.1.1 The siftUp Method
The siftUp method determines where an element is to be inserted, and performs the insertion while preserving the heap property. Here is the method specification and definition for siftUp:
/** * Inserts item x at position k, maintaining heap invariant by * promoting x up the tree until it is greater than or equal to * its parent, or is the root. * The worstTime(n) is O(log n) and averageTime(n) is constant. * * To simplify and speed up coercions and comparisons, the * Comparable and Comparator versions are separated into different * methods that are otherwise identical. (Similarly for siftDown.) * * @param k the position to fill * @param x the item to insert */ private void siftUp(int k, E x) { if (comparator != null) siftUpUsingComparator(k, x); else siftUpComparable(k, x); }
And here is the specification and definition for siftUpComparable (the definition for siftUpUsing-Comparator differs only in the use of the compare method instead of compareTo):
/** * Inserts item x at position k, maintaining heap invariant by * promoting x up the tree until it is greater than or equal to * (according to the elements' implementation of the Comparable * interface) its parent, or is the root. * The worstTime(n) is O(log n) and averageTime(n) is constant. * * @param k the position to fill * @param x the item to insert */ private void siftUpComparable(int k, E x) { Comparable<? super E> key = (Comparable<? super E>) x; while (k > 0) { int parent = (k - 1) >>> 1; Object e = queue[parent]; if (key.compareTo((E) e) >= 0) break; queue[k] = e; k = parent; } queue[k] = key; }
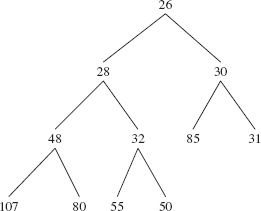
The siftUpComparable (int k, Ex) method restores the heap property by repeatedly replacing queue [k] with its parent and dividing k by 2 (with a right shift of 1 to accomplish dividing by 2 faster) until x is greater than or equal to the new parent. Then the while loop is exited and x is stored at queue[k]. Figure 13.4 shows the result of a call to siftUpComparable (10, new Integer (28)) on the complete binary tree in Figure 13.3:
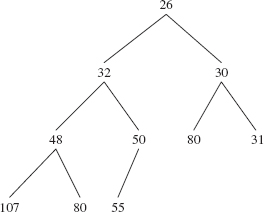
When called by the add (E element) method, the siftUp method starts at queue [size - 1] as the child and replaces that child with its parent until the parent is greater than or equal to the element to be inserted. Then the element is inserted at that parent index. For example, let's begin with the complete binary tree in Figure 3.3, repeated here, with 28 to be inserted:
FIGURE 13.4 The heap formed by invoking siftUp (10, new Integer(28)) on the complete binary tree in Figure 13.3
The child index is 10. Because 28 is less than 50, we replace queue[10] with 50, and set the child index to 4(= (10 − 1) >>> 1). See Figure 13.5.
FIGURE 13.5 The heap of Figure 13.3 after replacing queue[10] with queue[4]
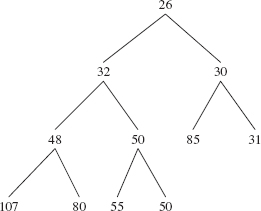
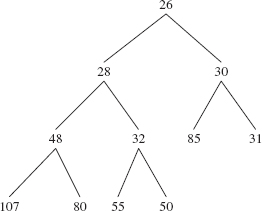
We now set the parent index to 1(= (4 − 1) >>> 1), and compare 28 with the parent's value, namely 32. Because 28 is less than 32, we replace queue[4] with queue[1], and set the parent index to 0(= (1 − 1) >>> 1). Because 28 is <= queue[0], 28 is inserted at queue[1] and that gives us the heap shown in Figure 13.6.
FIGURE 13.6 The heap formed when 28 is added to the heap in Figure 13.1
The key to the efficiency of the siftUp method is that a parent's index is readily computable from either of its children's indexes: if k contains a child's index, then its parent's index must be
(k-1)/2
or, to be slightly more efficient
(k −1) >>> 1 // >> performs a right shift of 1 bit on the binary representation of k - 1
And because queue is an array object, the element at that parent index can be accessed or modified in constant time.
In the worst case for the siftUp method, the element inserted will have a smaller value than any of its ancestors, so the number of loop iterations will be, approximately, the height of the heap. As we saw in Chapter 9, the height of a complete binary tree is logarithmic in n. So worstTime(n) is logarithmic in n, which satisfies the worst-time estimate from the specification of siftUp.
In the average case, about half of the elements in the heap will have a smaller value than the element inserted, and about half will have a larger value. But heaps are very bushy: at least half of the elements are leaves. And because of the heap properties, most of the larger-valued elements will be at or near the leaf level. In fact, the average number of loop iterations is less than 3 (see Schaffer [1993]), which satisfies the specification that averageTime(n) be constant. Programming Exercise 13.3 outlines a run-time experiment to support this claim.
Now we can analyze the add (E element) method. The worst case occurs when the array queue is full. Then a new, larger array is constructed and the old array is copied over. So worstTime(n) is linear in n. But this doubling occurs infrequently—once in every n insertions—so averageTime(n) is constant, just as for siftUp.
13.3.1.2 The element() and remove() Methods
The element() method simply returns the element at index 0, and so its worstTime(n) is constant.
/** * Returns the smallest-valued element in this PriorityQueue object. * * @return the smallest-valued element in this PriorityQueue object. * * @throws NoSuchElementException -if this PriorityQueue object is empty. * */ public E element() { if (size == 0) throw new NoSuchElementException(); return (E) queue [0]; } // method element()
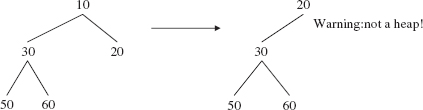
The remove() method's main task is to delete the root element. But simply doing this would leave a hole where the root used to be. So, just as we did when we removed a BinarySearchTree object's element that had two children, we replace the removed element with some other element in the tree. Which one? The obvious answer is the smaller of its children. And ultimately, that must happen in order to preserve the heap properties. But if we start by replacing the root element with its smaller child, we could open up another hole, as is shown in the following picture:
When 10 is replaced with 20, its smaller child, the resulting tree is not a heap because it is not a complete binary tree.
A few minutes reflection should convince you that, to preserve the completeness of the binary tree, there is only one possible replacement for the root element: the last element in the heap—at index size −1. Of course, we will then have a lot of adjustments to make; after all, we have taken one of the largest elements and put it at the top of the heap. These adjustments are handled in a siftDown method that starts at the new root and moves down to the leaf level. So the remove() method decrements size by 1, saves the element at index 0 in result, saves the element (no longer in the heap) at index size in x, calls siftDown(0, x) to place x where it now belongs, and returns result.
Here is the method definition:
/** * Removes the smallest-valued element from this PriorityQueue object. * The worstTime(n) is O(log n). * * @return the element removed. * * @throws NoSuchElementException - if this PriorityQueue object is empty. * */ public E remove () { if (size == 0) throw new NoSuchElementException(); int s = --size; modCount++; E result = (E) queue[0]; E x = (E) queue[s]; queue[s] = null; // to prevent memory leak if (s != 0) siftDown(0, x); return result; } // method remove
The definition of the siftDown (int k, E x) method is developed in Section 13.3.1.3.
13.3.1.3 The siftDown Method
To see how to define siftDown, let's start with the heap from Figure 13.1, repeated below:
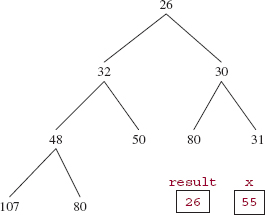
If we now call remove(), then 26 is saved in result and 55 is saved in x, just before the call to siftDown. See Figure 13.7.
FIGURE 13.7 A heap from which 26 is to be removed
Notice that since we started with a heap, the heap property guarantees that the root's left and right subtrees are still heaps. So siftDown's task is to maintain the heap property while putting x where it belongs.
In contrast to siftUp, the siftDown method works its way down the tree, starting at the index supplied as the argument, in this case, 0. Each parent is replaced with its smaller-valued child until, eventually, either x's value is less than or equal to the smaller-valued child (and then is stored at the parent index) or the smaller-valued child is a leaf (and then x is stored at that child index). For example, in the tree of Figure 13.7, 30 is smaller than 32, so 30 becomes the root element, and we have the tree shown in Figure 13.8.
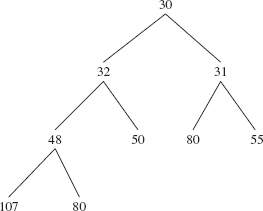
We still need one more iteration because 55 is greater than the smaller of the children (namely, 80 and 31 at indexes 5 and 6. So the element at index 6 (namely, 31) replaces the element at index 2 (namely, 30). That smaller-valued child was a leaf, so 55 is inserted at that leaf index and we end up with the heap shown in Figure 13.9.
If k contains the parent index, then k << 1 is the index of the left child and (k << 1) + 1 is the index of the right child (if the parent has a right child). And because queue is an array object, the elements at those indexes can be accessed or modified in constant time.
Here is the definition of siftDown:
private void siftDown(int k, E x) { if (comparator != null) siftDownUsingComparator(k, x);
FIGURE 13.8 The heap from Figure 13.7 after the smaller-valued of the root's children is replaces the root. The element 55 has not yet been removed
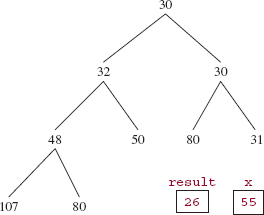
FIGURE 13.9 The heap formed from the heap in Figure 13.8 by replacing the element at index 2 with 31 and then inserting 55 at index 6
And here is siftDownComparable (which differs from siftDownUsingComparator in that the elements' class implements the Comparable interface):
/** * Maintains the heap properties in this PriorityQueue object while, starting at a * specified index, inserts a specified element where it belongs. * The worstTime(n) is O(log n). * * @param k -the specified position where the restoration of the heap * will begin. * @param x -the specified element to be inserted. * */ private void siftDownComparable(int k, E x) { Comparable<? super E> key = (Comparable<? super E>)x; int half = size >>> 1; // loop while a non-leaf while (k < half) { int child = (k << 1) + 1; // assume left child is least Object c = queue[child]; int right = child + 1; if (right < size && ((Comparable<? super E>) c).compareTo((E) queue[right]) > 0) c = queue[child = right]; if (key.compareTo((E) c) <= 0) break; queue[k] = c; k = child; } queue[k] = key; }
In the worst case for siftDownComparable, the loop will continue until a leaf replaces its parent. Since the height of a heap is logarithmic in n, worstTime(n) is logarithmic in n. Because a heap is a complete binary tree, the average number of loop iterations will be nearly log2 n, so averageTime(n)is also logarithmic in n.
In Lab 21, you will create a descendant, FairPQ, of the PriorityQueue class. As its name suggests, the FairPQ class resolves ties for highest-priority element in favor of seniority. For elements with equal priority, the highest-priority is chosen as the element that has been on the heap for the longest time.
You are now ready for Lab 21: Incorporating Fairness in Priority Queues
Section 13.4 shows how to modify the PriorityQueue class to obtain the heapSort method. Actually, the PriorityQueue class was created many years after the invention of the heapSort method, which was originally based on the idea of using an array to store a heap.
13.4 The heapSort Method
The heapSort method was invented by J.W.J. Williams (see Williams [1964]). Here is the method specification:
/**
* Sorts a specified array into the order given by the comparator in the
* constructor (natural, that is, Comparable order if default constructor;
* unnatural, that is, Comparator order if constructor specifies non-null
* comparator).
* The worstTime(n) is O(n log n) and worstSpace(n) is constant.
*
* @param a -the array object to be sorted.
*
* @throws NullPointerException - if a is null.
*
*/
public void heapSort (Object[ ] a)
Assume, for now, that this method is in the PriorityQueue class. Then the following is a test of that method:
public void testSample() { Integer [ ] expected ={12, 16, 17, 32, 33, 40, 43, 44, 46, 46, 50, 55, 59, 61, 75, 80, 80, 81, 87, 95}; Integer [ ] actual = {59, 46, 32, 80, 46, 55, 50, 43, 44, 81, 12, 95, 17, 80, 75, 33, 40, 61, 16, 87}; new PriorityQueue().heapSort (actual); assertArrayEquals (expected, actual); } // method testSample
Here is the basic idea of the heapSort method: We first initialize the queue and size fields:
queue = a;
int length = queue.length;
size = length;
We then heapify the array queue, that is, convert the array into a heap. After queue has become a heap, we sort queue into reverse order. Important: After each iteration of this loop, the heap will consist of the elements of queue from index 0 through index size—1, not through index queue.length-1. After the first sift down, the smallest element (the one with highest priority) will be at index queue.length - 1, and the array from indexes 0 through queue.length - 2 will constitute a heap. After the second sift down, the second smallest element will be at index queue.length - 2, and the array from indexes 0 through queue.length - 3 will constitute a heap. After all of the swaps and fix downs, the elements in the array queue will be in reverse order, so by reversing the order of the elements, the array will be in order.
For an example, let's start with an array of (references to Integer objects with the following) int values:
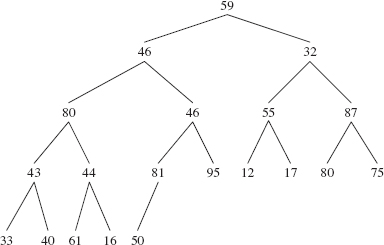
59 46 32 80 46 55 87 43 44 81 95 12 17 80 75 33 40 61 16 50
The value 59 is stored at index 0, the value 46 at index 1, and so on. Figure 13.10 (next page) shows the field queue viewed as a complete binary tree.
FIGURE 13.10 The array of 20 ints viewed as a complete binary tree
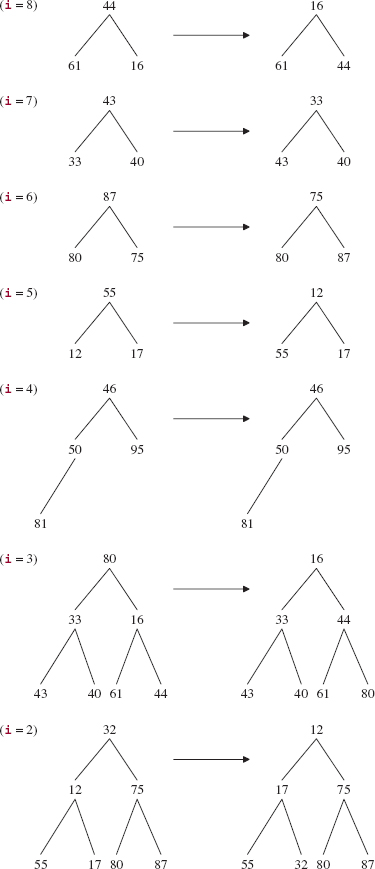
Of course, queue is not yet a heap. But we can accomplish that subgoal by looping as i goes from size - 1 down to 0. At the start of each iteration, the complete binary tree rooted at index i is a heap except, possibly, at index i itself. The call to siftDown (i, queue [i]) method in the PriorityQueue class converts the complete binary tree rooted at index i into a heap. So, basically, all we need to do is to repeatedly call siftDown (i, queue [i]) to create the heap from the bottom up.
We can reduce the number of loop iterations by half by taking advantage of the fact that a leaf is automatically a heap, and no call to siftDown is needed. So the loop will start at the last non-leaf index. For the complete binary tree rooted at that index, its left and right subtrees will be heaps, and we can call siftDown with that index as argument. In the above example, the last non-leaf index is 9, that is, 20/2 – 1. Since queue [19] is less than queue [9] —that is, since 50 is less than 81—the effect of the first iteration is that those two elements are swapped, giving the complete binary tree in Figure 13.11.
FIGURE 13.11 The complete binary tree of Figure 13.10 after swapping 50 with 81
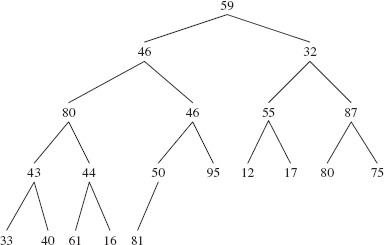
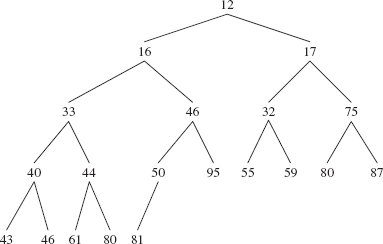
During the remaining 9 loop iterations (at indexes 8 through 0), we wind our way back up the tree. For the ith iteration, siftDown (i, queue [i]) is applied to the complete binary tree rooted at index i, with the left and right subtrees being heaps. The effects of the calls to siftDown (i, queue [i]) are as follows:
After the execution of siftDown (i, queue [i]) at index 0 in the final iteration, we get the heap shown in Figure 13.12.
FIGURE 13.12 The effect of making a heap from the complete binary tree in Figure 13.10
We now sort the array into reverse order. To accomplish this, we have another loop, this one with i going from index 0 to index queue.length - 1. During each loop iteration, we save the element at queue [-size] in x, store queue [0] in queue [size] and then call siftDown (0, x). For example, if i = 0 and size = 20, the element at queue [19] is saved in x, the smallest element (at index 0) is stored at queue [19], and siftDown (0, x) is called. The complete binary tree from index 0 through index 18 is a complete binary tree except at index 0, so the call to siftDown (0, x) will restore heapity to this subarray, without affecting the smallest element (now at index 19). The result of 20 of these loop iterations is to put the 20 elements in descending order in the array. Figure 13.13 shows this array in the form of a complete binary tree.
When we treat the complete binary tree in Figure 13.13 as an array, and reverse the elements in this array, the elements are in ascending order:
12 16 17 32 33 40 43 44 46 46 50 55 59 61 75 80 80 81 87 95
Here is the heapSort method:
public void heapSort (Object[ ] a)
{
queue = a;
FIGURE 13.13 The complete binary tree resulting from the heap of Figure 13.12 after the 20 swaps and sift downs
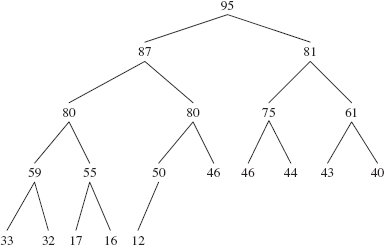
int length = queue.length; size = length; // Convert queue into a heap: for (int i = (size >> 1) - 1; i >= 0; i--) siftDown (i, (E)queue [i]); // Sort queue into reverse order: E x; for (int i = 0; i < length; i++) { x = (E)queue [--size]; queue [size] = queue [0]; siftDown (0, x); } // sort queue into reverse order // Reverse queue: for (int i = 0; i < length / 2; i++) { x = (E)queue [i]; queue [i] = queue [length - i - 1]; queue [length - i - 1] = x; } // reverse queue } // method heapSort
We earlier assumed that the heapSort method was part of the PriorityQueue class. Currently, at least, that is not the case. So how can we test and perform run-time experiments on that method? Surely, we cannot modify the PriorityQueue class in java.util. And we cannot make heapSort a method in an extension of the PriorityQueue class because the queue and size fields in that class have private visibility. What we do is copy the PriorityQueue class into a local directory, replace
package java.util;
with
import java.util.*;
And add the heapSort method to this copy of the PriorityQueue class. The method can then be tested and experimented with.
13.4.1 Analysis of heapSort
As with mergeSort in Chapter 11, we first estimate worstTime(n) for heapSort. The worst case occurs when the elements in the array argument are in reverse order. We'll look at the three explicit loops in heapSort separately:
- To convert queue to a heap, there is a loop with n/2 — 1 iterations and with i as the loop-control variable, and in each iteration, siftDown (i, queue [i]) is called. In the worst case, siftDown (i, queue [i]) requires log2(n) iterations, so the total number of iterations in converting a to a heap is O(n log n). In fact, it can be shown (see Concept Exercise 13.12) that this total number of iterations is linear in n.
- For each of the n calls to siftDown with 0 as the first argument, worstTime(n) is O(log n). Sothe total number of iterations for this loop is O(n log n) in the worst case.
- The reversing loop is executed n/2 times.
The total number of iterations in the worst case is O(n) + O(n logn) + O(n). That is, worstTime(n) is O(n log n) and so, by Sorting Fact 1 from Section 11.4, worstTime(n) is linear-logarithmic in n. Therefore, by Sorting Fact 3, averageTime(n) is also linear-logarithmic in n.
The space requirements are meager: a few variables. There is no need to make a copy of the elements to be sorted. Such a sort is called an in-place sort.
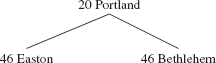
That heapSort is not stable can be seen if we start with the following array object of quality-of-life scores and cities ordered by increasing quality-of-life scores:
| 20 | Portland |
| 46 | Easton |
| 46 | Bethlehem |
Converting this array object to a heap requires no work at all because the heap property is already satisfied:
In the second loop of heapSort, Portland and Bethlehem are swapped and siftDown is called with 0 as the first argument:
Notice that, in the call to siftDown, (46 Bethlehem) is not swapped with (46 Easton) because its child (46 Easton) is not less than (46 Bethlehem). After two more iterations of the second loop and a reversal of the elements of the array, we have
| (20 Portland) | (46 Bethlehem) | (46 Easton) |
The positions of (46 Bethlehem) and (46 Easton) have flipped from the original array object, so the heapSort method is not stable.
13.5 Application: Huffman Codes
Suppose we have a large file of information. It would be advantageous if we could save space by compressing the file without losing any of the information. Even more valuable, the time to transmit the information might be significantly reduced if we could send the compressed version instead of the original.
Let's consider how we might encode a message file so that the encoded file has smaller size—that is, fewer bits—than the message file. For the sake of simplicity and specificity, assume the message file M contains 100,000 characters, and each character is either 'a', 'b', 'c', 'd', 'e', 'f', or 'g'. Since there are seven characters, we can encode each character uniquely with ceil (log27) bits,1 which is 3 bits. For example, we could use 000 for 'a', 001 for 'b', 010 for 'c', and so on. A word such as "cad" would be encoded as 010000011. Then the encoded file E need take up only 300,000 bits, plus an extra few bits for the encoding itself: 'a' = 000, and so on.
We can save space by reducing the number of bits for some characters. For example, we could use the following encoding:
a = 0
b = 1
c = 00
d = 01
e = 10
f = 11
g = 000
This would reduce the size of the encoded file E by about one-third (unless the character 'g' occurred very frequently). But this encoding leads to ambiguities. For example, the bit sequence 001 could be interpreted as "ad" or as "cb" or as "aab", depending on whether we grouped the first two bits together or the last two bits together, or treated each bit individually.
The reason the above encoding scheme is ambiguous is that some of the encodings are prefixes of other encodings. For example, 0 is a prefix of 00, so it is impossible to determine whether 00 should be interpreted as "aa" or "c". We can avoid ambiguities by requiring that the encoding be prefix-free, that is, no encoding of a character can be a prefix of any other character's encoding.
One way to guarantee prefix-free bit encodings is to create a binary tree in which a left branch is interpreted as a 0 and a right branch is interpreted as a 1. If each encoded character is a leaf in the tree, then the encoding for that character could not be the prefix of any other character's encoding. In other words, the path to each character provides a prefix-free encoding. For example, Figure 13.14 has a binary tree that illustrates a prefix-free encoding of the characters 'a' through 'g'.
To get the encoding for a character, start with an empty encoding at the root of the binary tree, and continue until the leaf to be encoded is reached. Within the loop, append 0 to the encoding when turning left and append 1 to the encoding when turning right. For example, 'b' is encoded as 01 and 'f' is encoded as 1110. Because each encoded character is a leaf, the encoding is prefix-free and therefore unambiguous. But it is not certain that this will save space or transmission time. It all depends on the frequency of each character. Since three of the encodings take up two bits and four encodings take up four bits, this encoding scheme may actually take up more space than the simple, three-bits-per-character encoding introduced earlier.
This suggests that if we start by determining the frequency of each character and then make up the encoding tree based on those frequencies, we may be able to save a considerable amount of space. The idea of using character frequencies to determine the encoding is the basis for Huffman encoding (Huffman [1952]). Huffman encoding is a prefix-free encoding strategy that is guaranteed to be optimal—among prefix-free encodings. Huffman encoding is the basis for the Unix compress utility, and also part of the JPEG (Joint Photographic Experts Group) encoding process.
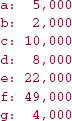
We begin by calculating the frequency of each character in a given message M. Note that the time for these calculations is linear in the length of M. For example, suppose that the characters in M are the letters 'a' ... 'g' as shown previously, and their frequencies are as given in Figure 13.15.
The size of M is 100,000 characters. If we ignored frequencies and encoded each character into a unique 3-bit sequence, we would need 300,000 bits to encode the message M. We'll soon see how far this is from an optimal encoding.
FIGURE 13.14 A binary tree that determines a prefix-free encoding of 'a' ... 'g'
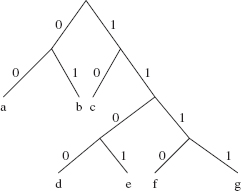
FIGURE 13.15 Sample character-frequencies for a message of 100,000 characters from 'a' ... 'g'
Once we have calculated the frequency of each character, we will insert each character-frequency pair into a priority queue ordered by increasing frequencies. That is, the front character-frequency pair in the priority queue will have the least frequently occurring character. These characters will end up being farthest from the root in the prefix-free tree, so their encoding will have the most bits. Conversely, characters that occur most frequently will have the fewest bits in their encodings.
Initially we insert the following pairs into the priority queue:
(a:5000) (b:2000) (c:10000) (d:8000) (e:22000) (f:49000) (g:4000)
In observance of the Principle of Data Abstraction, we will not rely on any implementation details of the PriorityQueue class. So all we know about this priority queue is that an access or removal would be of the pair (b:2000). We do not assume any order for the remaining elements, but for the sake of simplicity, we will henceforth show them in increasing order of frequencies—as they would be returned by repeated calls to remove().2 Note that there is no need to sort the priority queue.
13.5.1 Huffman Trees
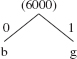
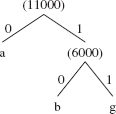
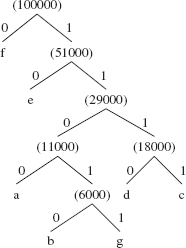
The binary tree constructed from the priority queue of character-frequency pairs is called a Huffman tree. We create the Huffman tree from the bottom up because the front of the priority queue has the least-frequently-occurring character. We start by calling the remove() method twice to get the two characters with lowest frequencies. The first character removed, 'b', becomes the left leaf in the binary tree, and 'g' becomes the right leaf. The sum of their frequencies becomes the root of the tree and is added to the priority queue. We now have the following Huffman tree
The priority queue contains
(a:5000) ( :6000) (d:8000) (c:10000) (e:22000) (f:49000)
Technically, the priority queue and the Huffman tree consist of character-frequency pairs. But the character can be ignored when two frequencies are summed, and the frequencies can be ignored in showing the leaves of the Huffman tree. And anyway, the algorithm works with references to the pairs rather than the pairs themselves. This allows references to represent the typical binary-tree constructs—left, right, root, parent—that are needed for navigating through the Huffman tree.
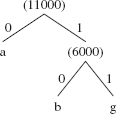
When the pairs (a:5000) and (:6000) are removed from the priority queue, they become the left and right branches of the extended tree whose root is the sum of their frequencies. That sum is added to the priority queue. We now have the Huffman tree:
(d:8000) (c:10000) ( :11000) (e:22000) (f:49000)
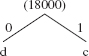
When d' and c' are removed, they cannot yet be connected to the main tree, because neither of their frequencies is at the root of that tree. So they become the left and right branches of another tree, whose root—their sum—is added to the priority queue. We temporarily have two Huffman trees:
and
The priority queue now contains
( :11000) ( :18000) (e:22000) (f:49000)
When the pair (:11000) is removed, it becomes the left branch of the binary tree whose right branch is the next pair removed, (:18000). The sum becomes the root of this binary tree, and that sum is added the priority queue, so we have the following Huffman tree:
The priority queue contains
(e:22000) ( :29000) (f:49000)
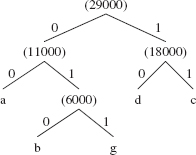
When the next two pairs are removed, e' becomes the left branch and (:29000) the right branch of the Huffman tree whose root, (:51000), is added to the priority queue. Finally the last two pairs, (f:49000) and (:51000) are removed and become the left and right branches of the final Huffman tree. The sum of those two frequencies is the frequency of the root, (:100000), which is added as the sole element into the priority queue. The final Huffman tree is shown in Figure 13.16.
FIGURE 13.16 The Huffman tree for the character-frequencies in Figure 13.15
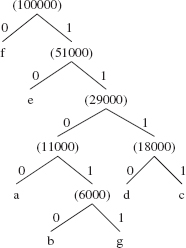
To get the Huffman encoding for'd', for example, we start at the leaf'd' and work our way back up the tree to the root. As we do, each bit encountered is pre-pended—placed at the front of—the bit string that represents the Huffman encoding. So the encoding in stages, is
0 10 110 1110
That is, the encoding for 'd' is 1110. Here are the encodings for all of the characters:
a: 1100 b: 11010 c: 1111 d: 1110 e: 10 f: 0 g: 11011
It is now an easy matter to translate the message M into an encoded message E. For example, if the message M starts out with
fad...
Then the encoded message E starts out with the encoding for 'f' (namely, 0) followed by the encoding for 'a' (namely, 1100) followed by the encoding for 'd' (namely, 1110). So E has
011001110...
What happens on the receiving end? How easy is it to decode E to get the original message M? Start at the root of the tree and the beginning of E, take a left branch in the tree for a 0 in E, and take a right branch for a 1. Continue until a leaf is reached. That is the first character in M. Start back at the top of the tree and continue reading E. For example, if M starts with "cede", then E starts with 111110111010. Starting at the root of the tree, the four ones at the beginning of E lead us to the leaf 'c'. Then we go back to the root, and continue reading E with the fifth 1. We take right branch for that 1 and then a left branch for the 0, and we are at 'e'. The next few bits produce 'd' and e'. In other words, we now have "cede", and that, as expected, is the start of M.
The size of the message E is equal to the sum, over all characters, of the number of bits in the encoding of the character times the frequency of that character in M. So to get the size of E in this example, we take the product of the four bits in the encoding of 'a' and the 5000 occurrences of 'a', add to that the product of the five bits in the encoding of 'b' and the 2000 occurrences of 'b', and so on. We get:
(4 * 5000) + (5 * 2000) + (4 * 10000) + (4 * 8000) + (2 * 22000) + (1 * 49000) + (5 * 4000)
= 215, 000
This is about 30% less than the 300,000 bits required with the fixed-length, 3-bits-per-character encoding discussed earlier. So the savings in space required and transmission time is significant. But it should be noted that a fixed-length encoding can usually be decoded more quickly than a Huffman encoding; for example, the encoded bits can be interpreted as an array index—the entry at that index is the character encoded.
13.5.2 Greedy Algorithm Design Pattern
Huffman's algorithm for encoding a message is an example of the Greedy Algorithm design pattern. In a greedy algorithm, locally optimal choices are made, in the hope that these will lead to a globally optimal solution. In the case of Huffman's algorithm, during each loop iteration the two smallest-valued elements are removed from the priority queue and made the left and right branches of a binary tree. Choosing the smallest-valued elements is locally optimal, that is, greedy. And the end result—globally optimal—is a minimal prefix-free encoding. So greed succeeds. We will encounter two more examples of greedy algorithms in Chapter 15; they also involve priority queues.
13.5.3 The Huffman Encoding Project
To add substance to the prior discussion, let's develop a project that handles the encoding of a message. The decoding phase is covered in Programming Project 13.1. The input will consist of a file path for the original message, and a file path denoting where the character codes and encoded message should be saved. For example, suppose that the file huffman.in1 contains the following message:
more money needed
System Test 1 (input in boldface):
Please enter the path for the input file: huffman.ini
Please enter the path for the output file: huffman.oul
After the execution of the program, the file huffman.ou1 will consist of two parts. The first part will have each character in the original message and that character's code. The second part, separated from the first by "**", will have the encoded message. Here is the complete file:
// the first line in the file is blank (see next paragraph) 0110 // the encoding for is 0110 1011 // the encoding for the blank character is 1011 d 100 e 11 m 001 n 000 o 010 r 0111 y 1010 ** 001010011111101100101000011101010110001111100111000110
In the encoding, the first character is the new-line marker, ' '. When the output file is viewed, the first line is blank because a new-line feed is carried out. The second line starts with a space, followed by the code for the new-line. This may seem a bit strange because the first line in the encoding is
0110
But when this line is printed, the new-line feed is carried out instead of ' ' being printed. So the space between ' ' and 0110 starts the second line. Subsequent lines start with the character encoded, a space, and the code for that character.
For System Test 2, assume that the file huffman.in2 contains the following message:
In Xanadu did Kubla Khan A stately pleasure-dome decree: Where Alph, the sacred river, ran Through caverns measureless to man Down to a sunless sea.
System Test 2 (input in boldface):
Please enter the path for the input file: huffman.in2
Please enter the path for the output file: huffman.ou2
Here is the complete file huffman.ou2 after execution of the program:
10001 101 , 001000 - 0100000 . 0100001 : 0010100 A 001011 D 0100110 I 0100101 K 001110 T 0011011 W 0010101 X 0011000 a 000 b 0011001 c 110010 d 11110 e 011 g 0011010 h 11111 i 001111 l 11101 m 110011 n 0101 o 11000 p 001001 r 1001 s 1101 t 10000 u 11100 v 010001 w 0100111 y 0100100 01001010101101001100000001010001111011100101111100011111111010100111 01110000110011110100010100111011111000010110001001011101110110000000 10000011111010100100101001001111010110001101111001001011010000011110 11000110011011101111100111100101001011011001010010001001010111111011 10010111010010111110100100111111001000101100001111101110111010001100 10100101111110101100100111101000101110010010001011001000010110001001 10111111110011100011100001101011111101110010000010001011100101011101 10111001101100011011110010010111110101111011101101100001100010111001 10000101100010100110110000100111010110110000110001010001011101111000 10111101011110111011011101011000010000110001
As always, we embrace modularity by separating the input-output details, in a HuffmanUser class, from the Huffman-encoding details, in a Huffman class. We start with the lower-level class, Huffman, in Section 13.5.3.1.
13.5.3.1 Design and Testing of the Huffman Class
The Huffman class has several responsibilities. First, it must initialize a Huffman object. Also, it must determine the frequency of each character. This must be done line-by-line so that the Huffman class can avoid entanglement in input-output issues. The other responsibilities are to create the priority queue and Huffman tree, to calculate the Huffman codes, and to return both the character codes and, line-by-line, the encoded message. From the discussion in Section 13.5.1, we want the Huffman class to be able to access the entries, that is, elements, in a priority queue or Huffman tree. For this we will create an Entry class. The Entry class has two fields related to the encoding, three fields related to binary-tree traversal, a compareTo method based on frequencies, and getFreq and getCode methods for the sake of testing:
public class Entry implements Comparable<Entry> { int freq; String code; Entry left, right, parent; public int compareTo (Entry entry) { return freq - entry.freq; } // compareTo public int getFreq() { return freq; } // method getFreq public String getCode() { return code; } // method getCode } // class Entry
We can now present the method specifications for the Huffman class. For the second through fifth of the following method specifications, the return values are only for the sake of testing.
/** * Initializes this Huffman object. * */ public Huffman() /** * Updates the frequencies of the characters in a scanned-in line. * * @param line - the line scanned in. * * @return - a cumulative array of type Entry in which the frequencies have been * updated for each character in the line. * */ public Entry[ ] updateFrequencies (String line) /** * Creates the priority queue from the frequencies. * * @return - the priority queue of frequencies (in increasing order). * */ public PriorityQueue<Entry> createPQ() /** * Creates the Huffman tree from the priority queue. * * @return - an Entry representing the root of the Huffman tree. * */ public Entry createHuffmanTree() /** * Calculates and returns the Huffman codes. * * @return - an array of type Entry, with the Huffman code * for each character. * */ public Entry[ ] calculateHuffmanCodes() /** * Returns, as a String object, the characters and their Huffman codes. * * @return the characters and their Huffman codes. * */ public String getCodes() /** * Returns a String representation of the encoding of a specified line. * * @param line - the line whose encoding is returned. * * @return a String representation of the encoding of line. * */ public String getEncodedLine (String line)
By convention, since no time estimates are given, you may assume that for each method, worstTime(n) is constant, where n is the size of the original message.
The Huffman methods must be tested in sequence. For example, testing the getCodes method assumes that the updateFrequencies, createPQ, createHuffmanTree, and calculateHuffman Codes are correct. Here is a test of the getCodes method, with huffman a field in the HuffmanTest class:
@Test
public void testGetCodes()
{
huffman.updateFrequencies ("aaaabbbbbbbbbbbbbbbbccdddddddd");
huffman.createPQ();
huffman.createHuffmanTree();
huffman.calculateHuffmanCodes();
assertEquals ("
0000
a 001
b 1
c 0001
d 01
", huffman.getCodes());
} // method testGetCodes
All of the files, including test files, are available from the book's website.
At this point, we can determine the fields that will be needed. Clearly, from the discussion in section 13.5.1, we will need a priority queue. Given a character in the input, it will be stored in a leaf in the Huffman tree, and we want to be able to access that leaf-entry quickly. To allow random-access, we can choose an ArrayList field or an array field. Here the nod goes to an array field because of the speed of directly utilizing the index operator, [], versus indirect access with the ArrayList's get and set methods. Note that if the original message file is very large, most of the processing time will be consumed in updating the frequencies of the characters and, later, in calculating the codes corresponding to the characters in the message file. Both of these tasks entail accessing or modifying entries.
That gives us two fields:
protected Entry [ ] leafEntries; protected PriorityQueue<Entry> pq;
For the sake of simplicity, we restrict ourselves to the 256 characters in the extended ASCII character set, so we have one array slot for each ASCII character:
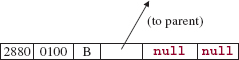
public final static int SIZE = 256;
For example, if the input character is 'B', the information for that character is stored at index (int) 'B', which is 66. If the encoding for 'B' is 0100 and the frequency of 'B' in the input message is 2880, then the entry at leafEntries [66] would be
The left and right references are null because leaves have no children. The reason that we use references rather than indexes for parent, left, and right is that some of the entries represent sums, not leaf-characters, so those entries are not in leafEntries. Every leaf is an entry, but not every entry is a leaf.
13.5.3.2 Definition of Methods in the Huffman Class
The definition of the default constructor is straightforward:
public Huffman() { Entry entry; leafEntries = new Entry [SIZE]; for (int i = 0; i < SIZE; i++) { leafEntries [i] = new Entry(); entry = leafEntries [i]; entry.freq = 0; entry.left = null; entry.right = null; entry.parent = null l; } // initializing leafEntries pq = new PriorityQueue<Entry>(); } // default constructor
The updateFrequencies method adds 1 to the frequency for each character in the parameter line. The new-line character is included in this updating to ensure that the line structure of the original message will be preserved in the encoding. Here is the method definition:
public Entry[ ] updateFrequencies (String line) { Entry entry; for (int j = 0; j < line.length(); j++) { entry = leafEntries [(int)(line.charAt (j))]; entry.freq++; } // for // Account for the end-of-line marker: entry = leafEntries [(int)' ']; entry.freq++; return leafEntries; } // method updateFrequencies
As noted earlier, worstTime(n) for this method is constant because n refers to the size of the entire message file, and this method works on a single line.
The priority queue is created from the entries with non-zero frequencies:
public PriorityQueue<Entry> createPQ() { Entry entry; for (int i = 0; i < SIZE; i++) { entry = leafEntries [i]; if (entry.freq > 0) pq.add (entry); } // for return pq; } // createPQ
The Huffman tree is created "on the fly." Until the priority queue consists of a single entry, a pair of entries is removed from the priority queue and becomes the left and right children of an entry that contains the sum of the pair's frequencies; the sum entry is added to the priority queue. The root of the Huffman tree is returned (for the sake of testing). Here is the definition:
public Entry createHuffmanTree() { Entry left, right, sum; while (pq.size() > 1) { left = pq.remove(); left.code = "0"; right = pq.remove(); right.code = "1"; sum = new Entry(); sum.parent = null; sum.freq = left.freq + right.freq; sum.left = left; sum.right = right; left.parent = sum; right.parent = sum; pq.add (sum); } // while return pq.element(); // the root of the Huffman tree } // method createHuffmanTree
The Huffman codes are determined for each leaf entry whose frequency is nonzero. We create the code for that entry as follows: starting with an empty string variable code, we pre-pend the entry's code field (either "0" or "1") to code, and then replace the entry with the entry's parent. The loop stops when the entry is the root. The final value of code is then inserted as the code field for that entry in leafEntries. For example, suppose part of the Huffman tree is as follows:
Then the code for 'B' would be "0100", and this value would be stored in the code field of the Entry at index 66 of leafEntries—recall that (int)'B' = 66 in the ASCII (and Unicode) collating sequence. Here is the method definition:
public Entry[ ] calculateHuffmanCodes() { String code; Entry entry; for (int i = 0; i < SIZE; i++) { code = ""; entry = leafEntries [i]; if (entry.freq > 0) { while (entry.parent != null) { code = entry.code + code; // current bit prepended to entry = entry.parent; // code as we go up the tree } // while leafEntries [i].code = code; } // if } // for return leafEntries; } // calculateHuffmanCodes
In the getCodes method, a String object is constructed from each character and its code, and that String object is then returned:
public String getCodes() { Entry entry; String codes = new String(); for (int i = 0; i < SIZE; i++) { entry = leafEntries [i]; if (entry.freq > 0) codes += (char)i + " " + entry.code + " "; } // for return codes; } // method getCodes
Finally, in the getEncodedLine method, a String object is constructed from the code for each character in line, appended by the new-line character, and that String object is returned:
public String getEncodedLine (String line) { Entry entry; String encodedLine = new String(); for (int j = 0; j < line.length(); j++) { entry = leafEntries [(int)(line.charAt (j))]; encodedLine += entry.code; } // for entry = leafEntries [(int)' ']; encodedLine += entry.code; return encodedLine; } // method getEncodedLine
13.5.3.3 The HuffmanUser Class
The HuffmanUser class has a main method to invoke a run method, a run method to open the input and output files from paths read in from the keyboard, a method to create the Huffman encoding, and a method to save the encoded message to the output file. Here are the method specifications for the createEncoding and saveEncodedMessage methods:
/** * Creates the Huffman encoding by scanning over a file to be encoded. * The worstTime(n) is O(n). * * @param fileScanner -a scanner over the file to be encoded. * @param huffman -an instance of the Huffman class. * * @return - a String consisting of each character and its encoding * */ public String createEncoding (Scanner fileScanner, Huffman huffman) /** * Saves the Huffman codes and the encoded message to a file. * The worstTime(n) is O(n). * * @param printWriter - the PrintWriter object that holds the Huffman codes * and the encoded message. * @param inFilePath - the String object that holds the path for the file * that contains the original message. * @param huffman - an instance of the Huffman class. * */ public void saveEncodedMessage (PrintWriter printWriter, String inFilePath, Huffman huffman)
The book's website has unit tests for the createEncoding and saveEncodedMessage methods, and Figure 13.17 has the UML diagram for the HuffmanUser class.
FIGURE 13.17 UML diagram for the HuffmanUser class

13.5.3.4 Method Definitions for the HuffmanUser Class
Here are the definitions of the main method, the default constructor, and the run method:
public static void main(String[]args) { new Huffman().run(); } // method main public void run() { final String IN_FILE_PROMPT = " Please enter the path for the input file: "; final String OUT_FILE_PROMPT = " Please enter the path for the output file: "; Huffman huffman = new Huffman(); PrintWriter printWriter = null; Scanner keyboardScanner = new Scanner (System.in), fileScanner = null; String inFilePath = null, outFilePath, line; boolean pathsOK = false; while (!pathsOK) { try { System.out.print (IN_FILE_PROMPT); inFilePath = keyboardScanner.nextLine(); fileScanner = new Scanner(new File (inFilePath)); System.out.print (OUT_FILE_PROMPT); outFilePath = keyboardScanner.nextLine(); printWriter = new PrintWriter (new FileWriter (outFilePath)); pathsOK = true; } // try catch (IOException e) { System.out.println (e); } // catch } // while !pathOK createEncoding (fileScanner, huffman); saveEncodedMessage (printWriter, inFilePath, huffman); } // method run
In that run method, the null assignments are needed to avoid a compile-time (" ... may not have been initialized") error for the arguments to the saveEncodedMessage method. That method is called outside of the try block in which inFilePath and printWriter are initialized.
In order to create the encoding, we will scan the input file and update the frequencies line-by-line. We then create the priority queue and Huffman tree, and calculate the Huffman codes. Most of those tasks are handled in the Huffman class, so we can straightforwardly define the createEncoding method:
public String createEncoding (Scanner fileScanner, Huffman huffman) { String line; while (fileScanner.hasNextLine()) { line = fileScanner.nextLine(); huffman.updateFrequencies (line); } // while fileScanner.close(); // re-opened in saveEncodedMessage huffman.createPQ(); huffman.createHuffmanTree(); huffman.calculateHuffmanCodes(); return getCodes(); } // method createEncoding
For the saveEncodedMessage method, we first write the codes to the output file, and then, for each line in the input file, write the encoded line to the output file. Again, the hard work has already been done in the Huffman class. Here is the definition of saveEncodedMessage:
public void saveEncodedMessage (PrintWriter printWriter, String inFilePath, Huffman huffman) { String line; try { printWriter.print (huffman.getCodes()); printWriter.println ("**"); // to separate codes from encoded message Scanner fileScanner = new Scanner (new File (inFilePath)); while (fileScanner.hasNextLine()) { line = fileScanner.nextLine(); printWriter.println (huffman.getEncodedLine (line)); } // while printWriter.close(); } // try catch (IOException e) { System.out.println (e); } // catch IOException } // method saveEncodedMessage
Later, another user may want to decode the message. This can be done in two steps:
- The encoding is read in and the Huffman tree is re-created. For this step, only the essential structure of the Huffman tree is needed, so the Huffman class is not used and the Entry class will have only three fields:
Entry left, right; char id; // the character that is a leaf of the treeThe root entry is created, and then each encoding is iterated through, which will create new entries and, ultimately, a leaf entry.
- The encoded message is read in, decoded through the Huffman tree, and the output is the decoded message, which should be identical to the original message. Decoding the encoded message is the subject of Programming Project 13.1.
SUMMARY
This chapter introduced the priority queue: a collection in which removal allowed only of the highest-priority element in the sequence, according to some method for comparing elements. A priority queue may be implemented in a variety of ways. The most widely used implementation is with a heap. A heap t is a complete binary tree such that either t is empty or
- the root element of t is smallest element in t, according to some method for comparing elements;
- the left and right subtrees of t are heaps.
Because array-based representations of complete binary trees allow rapid calculation of a parent's index from a child's index and vice versa, the heap can be represented as an array. This utilizes an array's ability to randomly access the element at a given index.
The PriorityQueue class's methods can be adapted to achieve the heapSort method, whose worstTime(n) is linear logarithmic in n and whose worstSpace(n) is constant.
An application of priority queues is in the area of data compression. Given a message, it is possible to encode each character, unambiguously, into a minimum number of bits. One way to achieve such a minimum encoding is with a Huffman tree. A Huffman tree is a two-tree in which each leaf represents a distinct character in the original message, each left branch is labeled with a 0, and each right branch is labeled with a 1. The Huffman code for each character is constructed by tracing the path from that leaf character back to root, and pre-pending each branch label in the path.
CROSSWORD PUZZLE
| ACROSS | DOWN |
| 1. The main advantage of Heap Sort over Merge Sort | 1. The averageTime(n) for the add (E element) in the PriorityQueue class |
| 4. Why an array is used to implement a heap | 2. Every heap must be a _______ binary tree. |
| 5. Every Huffman Tree is a ________. | 3. In a _______ algorithm, locally optimal choices lead to a globally optimal solution. |
| 6. A PriorityQueue object is not allowed to have any ______ elements. | 7. The field in the PriorityQueue class that holds the elements |
| 8. The prefix-free binary tree constructed from the priority queue of character-frequency pairs | |
| 9. Why (k - 1) >>> 1 is used instead of (k - 1)/2 |
CONCEPT EXERCISES
13.1 Declare a PriorityQueue object—and the associated Comparator -implementing class—in which the highest-priority element is the String object of greatest length in the priority queue; for elements of equal length, use lexicographical order. For example, if the elements are "yes", "maybe", and "no", the highest-priority element would be "maybe".
13.2 In practical terms, what is the difference between the Comparable interface and the Comparator interface? Give an example in which the Comparator interface must be used.
13.3 Show the resulting heap after each of the following alterations is made, consecutively, to the following heap:
- add (29);
- add (30);
- remove ();
- remove ();
13.4 For the following character frequencies, create the heap of character-frequency pairs (highest priority = lowest frequency):
- 5,000
- 2,000
- 10,000
- 8,000
- 22,000
- 49,000
- 4,000
13.5 Use the following Huffman code to translate "faced" into a bit sequence:
- 1100
- 1101
- 1111
- 1110
- 10
- 0
13.6 Use the following Huffman tree to translate the bit sequence 11101011111100111010 back into letters 'a'
13.7 If each of the letters 'a' through 'f' appears at least once in the original message, explain why the following cannot be a Huffman code:
- 1100
- 11010
- 1111
- 1110
- 10
- 0
13.8 Must a Huffman tree be a two-tree? Explain.
13.9 Provide a message with the alphabet 'a' ... 'e' in which two of the letters have a Huffman code of 4 bits. Explain why it is impossible to create a message with the alphabet 'a' ... 'e' in which two of the letters have a Huffman code of 5 bits. Create a message with the alphabet 'a' ... 'h' in which all of the letters have a Huffman code of 3 bits.
13.10 In Figure 13.16, the sum of the frequencies of all the non-leaves is 215,000. This is also the size of the encoded message E. Explain why in any Huffman tree, the sum of the frequencies of all non-leaves is equal to the size of the encoded message.
13.11 Give an example of a PriorityQueue object of ten unique elements in which, during the call to remove(), the call to siftDown would entail only one swap of parent and child.
13.12 This exercise deals with Heap Sort, specifically, the number of iterations required to create a heap from an array in reverse order. Suppose the elements to be sorted are in an array of Integer s with the following int values:
15, 14, 13, 12, 11, 10, 9, 8, 7, 6, 5, 4, 3, 2, 1
- Calculate the total number of loop iterations in the while loop of siftDownComparable or sift DownComparator to convert the array queue into a heap.
- Suppose n = 31 instead of 15, and the elements are still in reverse order. Calculate the total number of loop iterations in the while loop of siftDownComparable or siftDownComparator.
- Let n be one less than a power of 2—the complete binary tree will be full—and suppose the n elements are in reverse order. If we let h = floor(log2 n), we can develop a formula for calculating the number of while -loop iterations in the n/2 calls to siftDown. (For clarity, we will start calculating at the root level, even though the calls to siftDown start at level h − 1.) At the root level, there is one element, and the call to siftDown entails h loop iterations. At the next level down, there are two elements, and each of the corresponding calls to siftDown entails h − 1 loop iterations. At the next lowest level down, there are 4 elements, and each call to siftDown entails h − 2 iterations. And so on. Finally, at level h − 1, the next-to-leaf level, there are 2h−1 elements, and each call to siftDown (i) entails one loop iteration. The total number of while -loop iterations is:
Show that this sum is equal to n − floor(log2 n) − 1; there are also n/2 calls to siftDown. That is, for creating a heap from a full binary tree, worstTime(n) is linear in n.
Hint: By Exercise A2.6 in Appendix 2,
By Exercise A2.3 in Appendix 2,
By the Binary Tree Theorem, if t is a (non-empty) full binary tree of n elements and height h,
(n + 1)/2 = 2h
- Let t be a complete binary tree with n elements. Show that to make a heap from t, worstTime(n) is linear in n.
Hint: Let h be the height of t. For the number of while -loop iterations in siftDownComparable or siftDownComparator, compare the number of iterations, in the worst case, to make a heap from t with
- the number of iterations, in the worst case, to make a heap from the full binary tree t1 of height h − 1, and
- the number of iterations, in the worst case, to make a heap from the full binary tree t2 of height h.
PROGRAMMING EXERCISES
13.1 In Section 13.3.1, the PriorityQueueExample class creates a heap, pq1, of Student objects; the Student class implements the Comparable interface. Re-write the project so that the Comparator interface is implemented instead for pq1. Re-run the project to confirm your revisions.
13.2 Conduct a run-time experiment to support the claim that, on average, Heap Sort takes more time and uses less space than Merge Sort.
13.3 Conduct a run-time experiment to support the claim that averageTime(n) is constant for the add method in the PriorityQueue class. Hint: Copy the PriorityQueue class into one of your directories; replace the line package java.util; with import java.util.*;. Add a siftUpCount field, initialize it to 0, and increment it by 1 during the while loop in siftUpComparable (and in siftUpComparator). Define a public getSiftUpCount method that returns the value of siftUpCount. Create another class whose run method scans in a value for n, initializes a PriorityQueue<Integer> object with an initial capacity of n, fills in that PriorityQueue object with n randomly generated integer values, and prints out the value of siftUpCount divided (not integer division) by n. That quotient should be slightly less than 2.3.
Decoding a Huffman-Encoded Message
Suppose a message has been encoded by a Huffman encoding. Design, test, and implement a project to decode the encoded message and thus retrieve the original message.
Analysis For the entire project, worstTime(n) must be O(n), where n is the size of the original message. As shown in the output file in the Huffman project of this chapter, the input file will consist of two parts:
each character and its encoding;
the encoded message.
A sample input file, huffman.ou1, is shown in the following. The first line contains the carriage-return character, followed by a space, followed by its encoding. The carriage-return character, when viewed, forces a line-feed. So the first line below is blank, and the second starts with a space, followed by the code for the carriage-return character.
0010 0111 a 000 b 1 c 0011 d 010 e 0110 ** 1000010011100110110010011001110011000101110100001001001001100000100111 010000010011100110000100010111111111111111111111111111110010
System Test 1: (Input in boldface)
Please enter the name of the input file: huffman.ou1
Please enter the name of the output file: decode.ou1
The file decode.ou1 will contain:
bad cede cab dab dead dad cad bbbbbbbbbbbbbbbbbbbbbbbbbbbbb
Suppose the file huffman.ou2 contains the following (the message is from Coleridge's "Rubiyat of Omar Khayam"):
10001 101 , 001000 - 0100000 . 0100001 : 0010100 A 001011 D 0100110 I 0100101 K 001110 T 0011011 W 0010101 X 0011000 a 000 b 0011001 c 110010 d 11110 e 011 g 0011010 h 11111 i 001111 l 11101 m 110011 n 0101 o 11000 p 001001 r 1001 s 1101 t 10000 u 11100 v 010001 w 0100111 y 0100100 ** 01001010101101001100000001010001111011100101111100011111 11101010011101110000110011110100010100111011111000010110 00100101110111011000000010000011111010100100101001001111 01011000110111100100101101000001111011000110011011101111 10011110010100101101100101001000100101011111101110010111 01001011111010010011111100100010110000111110111011101000 11001010010111111010110010011110100010111001001000101100 10000101100010011011111111001110001110000110101111110111 00100000100010111001010111011011100110110001101111001001 01111101011110111011011000011000101110011000010110001010 01101100001001110101101100001100010100010111011110001011 1101011110111011011101011000010000110001
System Test 2:
Please enter the name of the input file: huffman.ou2
Please enter the name of the output file: decode.ou2
The file decode.ou2 will contain
In Xanadu did Kubla Khan A stately pleasure-dome decree: Where Alph, the sacred river, ran Through caverns measureless to man Down to a sunless sea.
Note: For the sake of overall efficiency, re-creating the Huffman tree will be better than sequentially searching the codes for a match of each sequence of bits in the encoded message.
Programming Project 13.2: An Integrated Web Browser and Search Engine, Part 5
In Part 4, you printed the search-results as they were obtained. In this part of the project, you will save the results, and then print them in decreasing order of frequencies. For example, if you ran System Test 1 from Part 4 (Programming Project 12.5), the output would now be
Here are the files and relevance frequencies, in decreasing order:
browser.in6 7
browser.in8 2
browser.in7 0
In saving the results, the data structure must satisfy the following:
to insert a result into the data structure, worstTime(n) must be O(n), and averageTime(n) must be constant;
to remove a result from the data structure, worstTime(n) and averageTime(n) must be O(log n);
System Test 1: (Assume search.in1 contains browser.in6, 7, 8 from Programming Project 12.5)
Please enter a search string in the input line and then press the Enter key.
neural network
Here are the files and relevance frequencies, in decreasing order:
browser.in6 7
browser.in8 2
browser.in7 0
System Test 2: (Assume search.ini contains browser.inIO, 11,12,13 -shown below)
Please enter a search string in the input line and then press the Enter key.
neural network
Here are the files and relevance frequencies, in decreasing order:
browser.in10 8
browser.in13 8
browser.in11 6
browser.in12 6
Here are the contents of the files from System Test 2:
browser.in10:
In Xanadu did Kubla Khan A stately <a href=browser.in3>browser3</a> pleasure-dome decree: Where Alph, the sacred river, <a href=browser.in4>browser4</a> ran Through caverns measureless to man Down to a <a href=browser.in5>browser5</a> sunless sea. neural network neural network neural network neural network And so it goes.
browser.in11:
In Xanadu did <a href=browser.in1>browser1</a> Kubla Khan A stately pleasure-dome decree: Where Alph, the neural network sacred river, ran Through caverns neural network measureless to man Down to a network sunless sea. network
browser.in12:
Neural surgeons have a network. But the decree is a decree is a network and a network is a network, neural or not.
browser.in13:
In Xanadu did Kubla Khan A stately <a href=browser.in3>browser3</a> pleasure-dome decree: Where Alph, the sacred river, <a href=browser.in4>>browser4</a> ran Through caverns measureless to man Down to a <a href=browser.in5>browser5</a> sunless sea. neural network neural network neural network neural network
Note 1: In your code, do not use complete path names, such as "h:Project3home.in1". Instead, use "home.in1".
1 Recall that ceil(x) returns the smallest integer greater than or equal to x.
2 In fact, if we did store the elements in a heap represented as an array, the contents of that array would be in the following order: (b:2000),(a:5000),(g:4000),(d:8000),(e:22000),(f:49000),(c:10000).