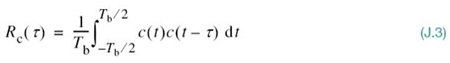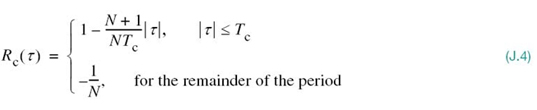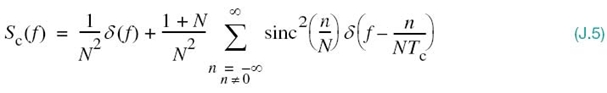APPENDIX

J  Maximal-Length Sequences

Basically, maximal-length sequences, also referred to in the literature as m-sequences, are linear cyclic codes, the generation of which is realized by using a linear feedback-shift register (LFSR) as discussed in Chapter 10 on error-control coding; Figure J.1 is an illustrative example of LFSR. However, from a practical perspective insofar as this book is concerned, it is the pseudo-noise (PN) characteristic that befits their use in producing spread-spectrum signals, an issue that was discussed in Section 9.13 of Chapter 9. In short, a maximal-length sequence viewed as a “carrier” may be used to spread the spectrum of an incoming message sequence in the transmitter and despread the received signal so as to recover the original message signal at the receiver output.

It is therefore apropos that we begin the discussion of maximal-length sequences in this appendix by discussing their basic properties, illustrated by the LFSR as the sequence generator.

J.1  Properties of Maximal-Length Sequences

Maximal-length sequences¹ have many of the properties possessed by a truly random binary sequence. A random binary sequence is a sequence in which the presence of binary symbol 1 or 0 is equally probable. Maximal-length sequences have the following properties.

PROPERTY 1  Balance Property

In each period of a maximal-length sequence, the number of 1s is always one more than the number of 0s.

PROPERTY 2  Run Property

Among the runs of 1s and of 0s in each period of a maximal-length sequence, one-half the runs of each kind are of length one, one-fourth are of length two, one-eighth are of length three, and so on as long as these fractions represent meaningful numbers of runs.

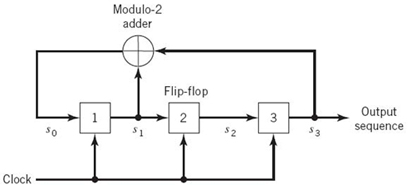
Figure J.1 Maximal-length sequence generator for m = 3, where m is the number of flip-flops in the generator.

By a “run” we mean a subsequence of identical symbols (1s and 0s) within one period of the sequence. The length of this subsequence is the length of the run. For a maximal-length sequence generated by a linear feedback shift register (LFSR) of length m, the total number of runs is (N + 1)/2, where N = 2^m – 1.

PROPERTY 3  Correlation Property

The autocorrelation function of a maximal-length sequence is periodic and binary valued.

As mentioned previously, the period of a maximum-length sequence is defined by

where m is the length of the LFSR. Let binary symbols 0 and 1 of the sequence be denoted by the levels –1 and +1, respectively. Let c(t) denote the resulting waveform of the maximal-length sequence, as illustrated in Figure J.2a for N = 7. Henceforth, the period of the waveform c(t) is

where T_c is the duration assigned to binary symbol 1 or 0 in the maximal-length sequence. Let c(t) denote the maximal-length sequence, the autocorrelation function of which is defined by

where the lag τ lies in the interval (–T_b/2, T_b/2). Applying this formula to c(t), we get

This result is plotted in Figure J.2b for the case of m = 3 or N = 7.

From Fourier transform theory, covered in Chapter 2, we know that periodicity in the time domain is transformed into uniform sampling in the frequency domain. This interplay between the time and frequency domains is borne out by the power spectral density of the maximal-length wave c(t). Specifically, taking the Fourier transform of (J.4), we get the sampled spectrum

which is plotted in Figure J.2c for m = 3 or N = 7. As N approaches infinity, S_c(f) approaches a continuous function of frequency f.

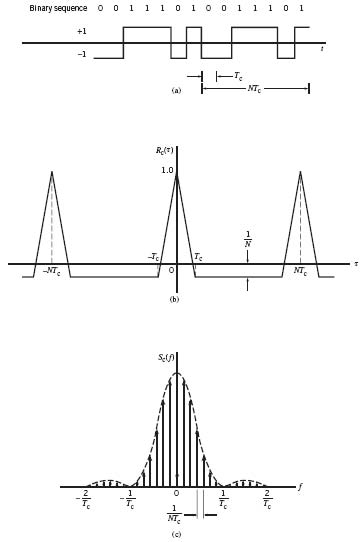
Figure J.2 (a) Waveform of maximal-length sequence for length m = 3 or period N = 7. (b) Autocorrelation function. (c) Power spectral density. All three parts refer to the output of the feedback shift register of Figure J.1.

Comparing the results of Figure J.2c for a maximal-length sequence with the corresponding results shown in Figure 4.12 of Chapter 4 on stochastic processes, for a random corresponding binary sequence, we may make two observations:

1.  For a period of the maximal-length sequence, the autocorrelation function R_c(τ) is somewhat similar to that of a random binary sequence.

2.  The waveforms of both sequences have the same envelope, sinc²(fT), for their power spectral densities. The fundamental difference between them is that whereas the random binary sequence has a continuous spectral density characteristic, the corresponding characteristic of a maximal-length sequence is discrete, consisting of delta functions spaced (1/NT_c) Hz apart.

As the shift-register length m or, equivalently, the period N of the maximal-length sequence is increased, the maximal-length sequence becomes increasingly similar to the random binary sequence. Indeed, in the limit, the two sequences become identical when N is made infinitely large. However, the price paid for making N large is an increasing storage requirement, which imposes a practical limit on how large N can actually be made in practical applications of spread spectrum modulation, for example.

J.2   Choosing a Maximal-Length Sequence

Now that we understand the properties of a maximal-length sequence and the fact that we can generate it using a linear feedback shift register, the key question that we need to address is:

How do we find the feedback logic for a desired period N?

The answer to this question is to be found in the theory of error-control codes, which is covered in Chapter 10. The task of finding the required feedback logic is made particularly easy for us by virtue of the extensive tables of the necessary feedback connections for varying shift-register lengths that have been compiled in the literature. In Table J.1 we present the sets of maximal (feedback) taps pertaining to shift-register lengths m = 2, 3,…, 8.² Note that, as m increases, the number of alternative schemes (codes) is enlarged. Also, for every set of feedback connections shown in this table, there is an “image” set that generates an identical maximal-length code, reversed in time sequence. Note also that the particular sets, identified with an asterisk in Table J.1, correspond to Mersenne prime length sequences, for which the period N is a prime number.

Table J.1 Maximal-length sequence of shift-register lengths 2–8

EXAMPLE 1  Maximal-Length Code Generation

Consider a maximal-length sequence requiring the use of a linear feedback-shift register of length m = 5. For feedback taps, we select the set [5, 2] from Table J.1. The corresponding configuration of the code generator is shown in Figure J.3a. Assuming that the initial state is 10000, the evolution of one period of the maximal-length sequence generated by this scheme is shown in Table J.2, where we see that the generator returns to the initial 10000 after 31 iterations; that is, the period is 31, which agrees with the value obtained from (J.2).

Suppose, next, we select another set of feedback taps from Table J.1, namely [5, 4, 2, 1]. The corresponding code generator is as shown in Figure J.3b. For the initial state 10000, we now find that the evolution of the maximal-length sequence is as shown in Table J.3. Here again, the generator returns to the initial state 10000 after 31 iterations, and so it should. But the maximal-length sequence generated is different from that shown in Table J.2.

Clearly, the code generator of Figure J.3a has an advantage over that of Figure J.3b, as it requires fewer feedback connections.

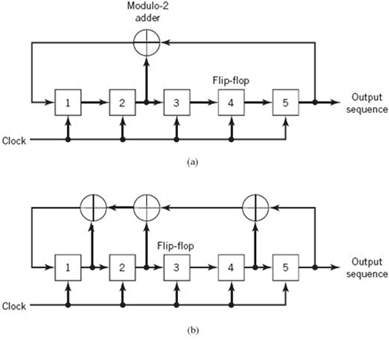
Figure J.3 Two different configurations of feedback shift register of length m = 5. (a) Feedback connections [5, 2]. (b) Feedback connections [5, 4, 2, 1].

Table J.2 Evolution of the maximal-length sequence generated by the feedback-shift register of Figure J.3a

Table J.3Evolution of the maximal-length sequence generated by the feedback-shift register of Figure J.3b

       Notes

1. For further details on maximal-length sequences, see Golomb (1967), Simon, et al. (1985: 283–295), and Peterson and Weldon (1972). The last reference includes an extensive list of polynomials for generating maximal-length sequences. For a tutorial paper on PN sequences, see Sarwate and Pursley (1980).

2. Table J.1 is extracted from the book by Dixon (1984: 81–83), where feedback connections of maximal-length sequences are tabulated for shift-register length m extending up to 89.