7 Automata

Various topics in theoretical computer science deal with the classification of formal languages with respect to their complexity, where different disciplines use different measures of “complexity.” Typically, a formal language is a subset of a finitely generated free monoid Σ∗. The word “formal” serves to distinguish these languages from natural languages. In many cases, we omit this adjective and call L ⊆ Σ∗ a language. The classification of languages can be done from rather different points of view. A well-known approach is the Chomsky hierarchy by Avram Noam Chomsky (born 1928), where grammars are used as description mechanisms. The class of regular languages coincides with Type-3 in Chomsky’s hierarchy. This class is particularly robust as it admits various other natural characterizations. In this chapter, we examine regular languages not only within free monoids but also in arbitrary monoids. The two main mechanisms to describe regular languages, regular expressions and deterministic finite state automata, lead to different classes. Therefore, we distinguish between rational and recognizable sets. We will see that rational sets correspond to nondeterministic finite automata and regular expressions, whereas deterministic finite-state automata define recognizable sets. Moreover, there are finitely generated monoids where the class of rational subsets is strictly larger than the class of recognizable sets. Section 7.3 shows that the concepts rational and recognizable coincide over finitely generated free monoids, which allows an unambiguous use of the term regular in this context.

Let L and K be the subsets of a monoid M. The product L ⋅ K is defined by L ⋅ K = { uυ | u ∈ L, υ ∈ K }. Moreover, we let L0 = {1} and Ln+1 = L ⋅ Ln for n ∈ ℕ. Thus, we can define the submonoid generated by L as follows:

By definition, L∗ is the smallest submonoid of M which contains L. The operation L ↦ L∗ is called the Kleene star after Stephen Cole Kleene (1909–1994) or simply the star operation. The Kleene star depends on the ambient monoid M; it must not to be confused with the notation for the free monoid over L. For example, the Kleene star of {a, aa} for a ∈ Σ contains the word aaa = a ⋅ aa = aa ⋅ a = a ⋅ a ⋅ a. However, in the free monoid generated by the alphabet {a, aa}, the words a ⋅ aa, aa ⋅ a and a ⋅ a ⋅ a are all different. Frequently, we use shorthands, for example, we may write LK instead of L ⋅ K or, if u ∈ M, then we identify u with the singleton {u}. It is also common to write L + K to denote the union L ∪ K.

7.1 Recognizable sets

The concept of recognizability is based on an algebraic approach to formal language theory. It is particularly well suited to describe the “complexity” of subclasses of regular languages and to decide their membership in subclasses. Star-free languages are the most prominent of one of these subclasses and we discuss them in Section 7.4.

Let M and N be monoids. Typically, N is finite. A subset L ⊆ M is recognized by a homomorphism φ: M → N if L = φ−1(φ(L)). In this case, we say that N recognizes the set L ⊆ M. A subset of M is called recognizable if it is recognized by a finite monoid N. The set of all recognizable subsets of M is denoted by REC(M). If φ is given by the images of a generating set Σ of M, then we can test membership of u ∈ L for u = a1 ⋅⋅ ⋅ an with ai ∈ Σ by a “table look-up,”we compute φ(u) = φ(a1) ⋅⋅ ⋅ φ(an) in N and check whether φ(u) belongs to the finite table φ(L) ⊆ N.

Remark 7.1. In a finite monoid M, every subset of Mis recognized by the identity mapping M → M. In particular, finite subsets of a finite monoid are recognizable. In a group G the converse holds; if the finite subsets are recognizable, then G is finite. Indeed, let N be finite and φ: G → N be a surjective homomorphism recognizing the singleton {1}. Then N is a group and {1} is the preimage of the neutral element of N. Therefore, the kernel of φ: G → N is trivial. This means that φ is injective. Hence, G is finite because N is finite.

◊

Theorem 7.2. The class of recognizable sets over a monoid M is a Boolean algebra. This means, it is closed under finite union, finite intersection, and complementation. It is also closed under inverse homomorphisms. This means, if ψ: M' → M is a homomorphism and if L ∈ REC(M), then ψ−1(L) ∈ REC(M).

Proof: Every finite monoid recognizes 0 and M. This shows the closure under empty union and empty intersection. Let L1, L2 be recognizable sets and for i = 1, 2, let φi : M → Ni be a homomorphismwith Li = φ−i 1 (Fi) where Fi = φi(Li). The homomorphism φ1 : M → N1 also recognizes the complementML1. Consider ψ: M → N1×N2 with ψ(u) = (φ1(u), φ2(u)). Thenψ−1(F1×F2) = L1∩L2 and ψ−1((F1×N2)∪(N1×F2)) = L1 ∪ L2.

□

Let ψ: M' → M be a homomorphism and let L ⊆ M be recognized by φ: M → N, then ψ−1(L) ⊆ M' is recognized by φ ∘ ψ: M' → N. This shows that the class of recognizable sets is closed under inverse homomorphisms.

We have just seen that recognizable sets are closed under inverse homomorphisms, but, in general, they are not closed under homomorphisms. Consider, for example, the homomorphism ψ: {a, b}∗ → ℤwith a ↦ 1 and b ↦ −1. The singleton {ε} ⊆ {a, b}∗ is recognizable in {a, b}∗, but ψ({ε}) = {0} ⊆ ℤ is not recognizable in ℤ by Remark 7.1. Actually, no nontrivial subset of a∗ is recognizable in the group ℤ. The following example yields an even stronger “nonclosure"property.” It was given by Shmuel Winograd (born 1936) and shows that, in general, recognizable sets are neither closed under product nor under Kleene star.

Example 7.3. We extend the addition from ℤ to M = ℤ∪ {e, a} to an operation on M by e + m = m + e = m for m ∈ M, a + a = 0, and a + k = k + a = k for k ∈ ℤ. This way M = (M, +, e) forms a commutative monoid with e as its neutral element. Consider a homomorphism φ: M → N with φ−1(φ(L)) = L, and let φ̃ : ℤ → N be the restriction of φ to ℤ ⊆ M.With F = φ(L) we have φ̃ −1(F) = φ−1(F) ∩ℤ = L ∩ℤ. Thus, L ∈ REC(M) implies L ∩ ℤ ∈ REC(ℤ). By Remark 7.1, we obtain {0} ∉ REC(ℤ). Next, we show that {a} ∈ REC(M). Let N = {e, a, n} be a commutative monoid with neutral element e, zero element n and a+a = n. Let φ: M → N be the homomorphismwith e ↦ e, a ↦ a and k ↦ n for k ∈ ℤ. Then φ−1(a) = {a} and therefore {a} ∈ REC(M). On the other hand, L1 = {a} + {a} = {0} and L2 = {a}∗ = {e, a, 0} are not in REC(M), because otherwise also Li ∩ℤ = {0} ∈ REC(ℤ).

◊

A congruence in a monoid M generalizes the notion of “being congruent modulo n” for integers. By definition, it is an equivalence relation ≡ ⊆ M × M such that u ≡ υ implies xuy ≡ xυy for all u, υ, x, y ∈ M. For u ∈ M, let [u] = {υ ∈ M| u ≡ υ } be its congruence class. The set of congruence classes { [u] | u ∈ M } is denoted by M / ≡ and it forms a monoid with the multiplication

The operation is well defined because u ≡ u' and υ ≡ υ' yields

From the corresponding properties of the monoid M, it follows that the operation on M / ≡ is associative with [1] as neutral element. (It follows “par transport de structures.”) Moreover, the mapping μ : M → M / ≡ with μ(u) = [u] is a surjective homomorphism.

Let L be any subset of M. Then we assign to L the syntactic congruence ≡L by letting u ≡L υ if

Hence, u can “syntactically” be replaced by υ in any context without changing the membership with respect to L. The relation ≡L is obviously a congruence and the congruence classes form the syntactic monoid of L. It is denoted by Synt(L). The syntactic monoid Synt(L) recognizes the subset L (i.e., μ−1(μ(L)) = L) because for μ(u) = μ(υ) either u, υ ∈ L or u, υ ∉ L. The next theorem implies that Synt(L) is the minimal monoid recognizing L.

Theorem 7.4. Let L ⊆ M and φ: M → N be a homomorphism with L = φ−1(φ(L)). Then, by φ(u) ↦ [u], a surjective homomorphism from the submonoid φ(M) ⊆ N to Synt(L) is defined.

Thus [u] = [υ]. Furthermore, φ(M) → Synt(L) : φ(u) ↦ [u] is a surjective mapping. The homomorphism property now follows from 1 = φ(1) ↦ [1], φ(uυ) = φ(u)φ(υ) as well as φ(uυ) ↦ [uυ] and φ(u)φ(υ) ↦ [u][υ] for all u, υ ∈ M.

Another concept related to recognizability by monoids is acceptance by deterministic automata. An M-automaton A = (Q, ⋅, q0, F) consists of a set of states Q, an initial state q0 ∈ Q, a set of final states F ⊆ Q, and a transition function ⋅ : Q × M → Q satisfying the following properties for all q ∈ Q and u, υ ∈ M.

We define the set L(A) that is accepted by the M-automaton A by

In mathematical terms, Q is a set where M acts on the right. We can also think that, by reading an element u ∈ M in a state q,we move from q to state q ⋅ u.

Choosing a generating set Σ ⊆ M, we may represent M-automata as edge-labeled directed graphs. The states are the vertices and, in our graphical representation, an initial state is marked by an incoming arrow, whereas final states are characterized by double circles. We let δ = {(p, u, p ⋅ u) | p ∈ Q, u ∈ Σ } and we draw an edge from p to p ⋅ u which is labeled by u. The edges in this graph are called transitions. If we refer to this representation, we also denote an M-automaton as a tuple A = (Q, Σ, δ, q0 , F). We use the following convention in pictures.

To determine p ⋅ u for arbitrary pairs (p, u) ∈ Q × M, it is sufficient to factorize u = u1 ⋅⋅ ⋅ un with ui ∈ Σ and then follow the states p, p ⋅ u1, . . . , p ⋅ u1 ⋅⋅ ⋅ un successively. Since Σ is a generating set, this path from p to p ⋅ u exists. M-automata defined this way are complete and deterministic. The automaton is complete because the transition function ℚ × Σ → Q, (q, u) ↦ q ⋅ u is totally defined. It is deterministic because, for each q ∈ Q and for each u ∈ M, there is at most one state q ⋅ u. (In Section 7.2, we extend this concept to nondeterministic M -automata.)

We say that a state q ∈ Q is reachable if there is some u ∈ M with q = q0 ⋅ u. Without loss of generality, we can assume that all states are reachable, because removing an unreachable state does not change the accepted set L(A). Let Σ ≠ 0. Since an M-automaton is complete, we see that δ is finite if and only if Q and Σ are finite. Thus, if M is not finitely generated, then δ is always infinite. If M is finitely generated, then we can choose Σ to be finite and we see that δ is finite if and only if the set of reachable states is finite.

Example 7.5. The set {−1, +1} is a generating set of the monoid ℤ of integers, with the addition as monoid operation. The ℤ-automaton A, defined by A = ({0, 1, 2, 3, 4, 5}, δ, 0, {1, 4}) with δ(q, k) = (q + k) mod 6 has the following graphical representation:

The set accepted by A is L(A) = { k + 6ℓ | k ∈ {1, 4}, ℓ ∈ ℤ}.

◊

To every subset L ⊆ M, you can assign a canonical automaton, which is called the minimal automaton of L. For this purpose, we first define the quotient by an element u ∈ M by L(u) = { υ ∈ M | uυ ∈ L }. These subsets are interpreted as states. L(u) is also commonly denoted by u−1L which is closer to the notation of a (left) quotient. Note that L = L(1) and this is the natural initial state. Formally, the minimal automaton AL of L ⊆ M is defined as follows:

Let L(u) = L(u). Then

This shows that L(uυ) = L(uυ). As a consequence, L(u) ⋅ υ is well defined; it does not depend on the choice of representatives for the class L(u). Moreover, L(u) ⋅ 1 = L(u) and (L(u) ⋅ υ) ⋅w = L(uυ) ⋅w = L(uυw) = L(u) ⋅υw. The minimal automaton AL accepts exactly the set L, because L(1) ⋅ u = L(u), and u ∈ L is equivalent to 1 ∈ L(u).

Example 7.6. We consider the set L = {k + 6ℓ | k ∈ {1, 4}, ℓ ∈ ℤ} as in Example 7.5. Adding multiples of 3 does not change membership in L. It therefore suffices to determine the languages L(0), L(1) and L(2): L(0) = 1+3ℤ, L(1) = 3ℤ and L(2) = −1+3ℤ. This yields the following minimal automaton AL:

◊

The following theorem justifies the name “minimal” automaton.

Theorem 7.7. Let L ⊆ M be accepted by an M-automaton A = (Q, Σ, ⋅, q0 , F) and AL the minimal automaton of L. Then q0 ⋅ u ↦ L(u) is a surjective mapping from the set of reachable states of A onto the set of states in AL. In particular, the number of states of AL is at most the number of states of A.

Proof: From q = q0 ⋅ u, we immediately obtain L(u) = {υ | q ⋅ υ ∈ F }. Therefore, the mapping q0 ⋅ u ↦ L(u) is well defined. It is surjective, since for each u ∈ M the reachable state q0 ⋅ u is a preimage of L(u).

□

Automata minimization

Theorem 7.7 implicitly provides a minimization method for M-automata. For a state p ∈ Q, let L(p) = {υ ∈ M | p ⋅ υ ∈ F} be the language at p. The set accepted by A is exactly the language at the initial state. Moreover, we see that L(p) = L(q) implies L(p⋅u) = L(q⋅u) for all u ∈ M. Let us merge states which define the samelanguage into a single class [p] and let [p] ⋅ u = [p ⋅ u]. Then Theorem 7.7 tells us that the mapping q0 ⋅ u ↦ L(u) induces a bijection between { [p] | p ∈ Q is reachable } and the states { L(u) | u ∈ M } of the minimal automaton.

The following marking algorithm by Edward Forrest Moore (1925–2003) [77] is applied to an M-automaton with states Q and δ ⊆ Q ×Σ×Q. After preprocessing we know that all states are reachable from the initial state q0.Now, in a first phase, the algorithm marks pairs of states whose components define different languages as explained below. Then, in a second phase one chooses a representative from each set of unmarked states. The first of the two phases satisfies the invariant that a pair (p, q) ∈ Q × Q is only marked if L(p) ≠ L(q). The first phase works as follows:

This concludes the first phase. Let us see that the invariant L(p) ≠ L(q) holds for all marked pairs (p, q). This is certainly true if, say, p is final and q is not final because then 1 ∈ L(p) L(q). Now, consider a marked pair (p'' , q'). By induction (and by symmetry in p' and q') we may assume that there is some u' ∈ L(p) L(q'). The algorithm marks all pairs (p, q) ∈ P with {p' , q'} = {p ⋅ a, q ⋅ a} for a ∈ Σ. This implies u = au' ∈ (L(p) L(q)) ∪ (L(q) L(p)). Thus, the invariant L(p) ≠ L(q) is satisfied. As a consequence, if there are p, q ∈ Q with p < q and L(p) = L(q), then the pair (p, q) has not been deleted and it is still a member of P. We also need the converse. Let (p, q) ∈ P with L(p) ≠ L(q) and let u ∈ (L(p) L(q)) ∪ (L(q) L(p)). If |u| = 0, then (p, q) is marked in step (3) and deleted. In the other case we have u = aυ and υ ∈ (L(p ⋅ a) L(q ⋅ a)) ∪ (L(q ⋅ a) L(p ⋅ a)). By induction on |u|, either the pair (p ⋅ a, q ⋅ a) or the pair (q ⋅ a, p ⋅ a) is marked. This implies that (p, q) is marked and then deleted in this case, as well.

In the following, we only consider the remaining pairs (p, q) in P. The idea for the second phase is based on the following observation. If we view (p, q) as an undirected edge {p, q}, then, in the resulting undirected graph (Q, P), connected components are cliques. The languages at all states in the same clique are equal and can be identified with the states of AL.

So in the second phase, we assign to every p ∈ Q a state ̂p which is in the same connected component of p. Say, p̂ is minimal with respect to the chosen linear order of Q. There are various ways to do this algorithmically; and one can choose any of them. The set ̂Q = { p̂ | p ∈ Q } is in canonical bijection with the set of states in the minimal automaton AL. The bijection is induced by mapping p = q0 ⋅ u to the quotient L(u). Since we started with an automaton where every state is reachable, we can write p = q0 ⋅ u for some u and the mapping q0 ⋅ u ↦ L(u) is well defined and injective on Q̂ by construction of the ̂δgraph. Finally, we let= {(p̂, a, q̂) | (p, a, q) ∈ δ }. Then, the automaton (̂Q, Σ, ̂δ, ̂q0, F ∩ Q̂) is, up to renaming, the same M-automaton as the minimal automaton AL.

Syntactic monoids as transition monoids

To an M-automaton A = (Q, ⋅, q0 , F), we assign its transition monoid by the canonical interpretation of an element in M as a mapping on states; for u ∈ M we define the mapping δu : Q → Q by δu(q) = q ⋅ u. The transition monoid of A is the submonoid { δu | u ∈ M} of the monoid { f : Q → Q | f is function } of all mappings from Q to Q. We have δυ(δu(q)) = q ⋅ uυ = δuυ(q) for all q ∈ Q. Thus, the operation δu ⋅ δυ = δuυ is well defined. The homomorphism that maps u ∈ M to δu recognizes L(A) because we have u ∈ L(A) if and only if δu(q0)∈ F.

Theorem 7.8. There is a canonical isomorphism between the syntactic monoid of L ⊆ M and the transition monoid of the minimal automaton AL.

Proof: Let T be the transition monoid of AL. By Theorem 7.4 the homomorphism δu ↦ [u] is a surjection from T onto the syntactic monoid Synt(L). We only have to show that it is injective. So let [u] = [υ], that is, u ≡L υ. For a state L(x) = { y | xy ∈ L } in AL we have δu(L(x)) = L(x) ⋅ u = L(xu). For all y ∈ M this yields the equivalence

□

and therefore δu(L(x)) = δυ(L(x)). This shows δu = δυ.

The following theorem by John R. Myhill, Sr. (1923–1987) and Anil Nerode (born 1932) states that recognizability and acceptance by M-automata with finitely many states are equivalent [81].

Theorem 7.9 (Myhill, Nerode). Let L ⊆ M. The following statements are equivalent:

Proof: (a) ⇒ (b): Let N be a finite monoid and φ: M → N a homomorphism with φ−1(φ(L)) = L. We define a finite M-automaton AN = (N, ⋅, 1N , φ(L)) with n ⋅ u = n φ(u). Now

□

that is, AN accepts the set L. (b) ⇒ (c). This follows from Theorem 7.7. (c) ⇒ (d). If AL has only finitely many states Q L, then there are only finitely many mappings from Q L to QL. Therefore, the transition monoid of AL is finite and thus, by Theorem 7.8, so is the syntactic monoid Synt(L). (d) ⇒ (a): This follows, since the syntactic monoid Synt(L) recognizes the set L.

7.2 Rational sets

In this section, we introduce rational sets and extend the concept of M -automata to nondeterministic automata. Rational expressions define rational sets and we show that rational sets and nondeterministic finite M-automata have the same expressive power. The family RAT(M) of rational sets over a monoid M is inductively defined as follows:

Here, as defined previously, KL = K ⋅ L = {uυ ∈ M| u ∈ K, υ ∈ L }, and L∗ denotes the submonoid of M generated by L. The definition of a rational set is given together with its semantics as a subset of M. Sometimes it is useful to distinguish between the subset L and its syntactic description as a rational (or regular) expression. If + is not used for the monoid operation, then the syntactic operator + has the same meaning as ∪, so a finite set L = {u1, . . . , uk} is given by the expression u1 + ⋅ ⋅⋅ + uk, too. If k = 0, then we use 0 as an expression. We define KL, and L∗ to be rational expressions if K and L are rational expressions. Moreover, brackets are used to avoid ambiguity, for example, the expression a(b + c)∗ is another syntax for {a}{b, c}∗. However, for the monoid M = ℕ×ℕ×ℕwith addition + as operation, the expression (0, 2, 4) + ((0, 1, 2)∪(1, 0, 2))∗ denotes {(0, 2, 4)}{((0, 1, 2), (1, 0, 2))}∗. So, this is a case where + does not mean “union.” We will make sure that there is no risk of confusion. In M as above, the expression (0, 2, 4) + ((0, 1, 2) ∪ (1, 0, 2))∗ describes the set

Remark 7.10. The class of rational sets is closed under homomorphisms. Indeed, let ψ: M → M' be a homomorphism and let L, K ⊆ M be any languages. If L is finite, then ψ(L) is finite. Moreover, ψ(L ∪ K) = ψ(L) ∪ ψ(K), ψ(L ⋅ K) = ψ(L) ⋅ ψ(K), and ψ(L∗) = (ψ(L))∗.

◊

A nondeterministic M-automaton A = (Q, δ, I, F) consists of a set of states Q, a transition relation δ ⊆ Q × M × Q, a set of initial states I ⊆ Q, and a set of final states F ⊆ Q. It is called finite if δ is a finite set. The elements of δ are called transitions, and the element u ∈ M is the label of the transition (p, u, q). Roughly speaking, the automaton A decorates the elements of M with states, by assigning to each u ∈ M possible runs. A run on A is a sequence of the form

with (qi , ui , qi+1) ∈ δ for all 1 ≤ i ≤ n. We say r is a run on u ∈ M, if u = u1 ⋅⋅ ⋅ un; it is accepting if q1 ∈ I and qn+1 ∈ F. The accepted set of A is

Two M -automata are equivalent if they accept the same set. For a given generating set Σ of M, an automaton A is called spelling if δ ⊆ Q × Σ × Q, that is, if all labels are elements of Σ. A spelling nondeterministic M-automaton is called complete if for each state p ∈ Q and each a ∈ Σ, there exists some (p, a, q) ∈ δ. It is called deterministic if the set of initial states I contains exactly one state and if for each state p ∈ Q and each element u ∈ M there is at most one state q ∈ Q such that there is a run pu1q1 ⋅⋅ ⋅ unqn with u = u1 ⋅⋅ ⋅ un and qn = q. For a complete and deterministic spelling automaton, we can define p ⋅ u = q and we obtain an M-automaton in the sense of Section 7.1. Conversely, by choosing a generating set Σ for M, each M-automaton as defined in Section 7.1 can be converted into a complete and deterministic spelling automaton in the in the sense given earlier. The notion of nondeterministic M-automaton is therefore more general than the term M-automaton as used before.

The following automaton over the monoid ℕ×ℕwith addition as operation recognizes the set { (m, n) | m = n − 4, m even }:

For the conversion of rational sets to nondeterministic automata, we use the Thompson construction [103] named after Kenneth Lane Thompson (born 1943). He is a well-known computer science pioneer and primarily known for his work as a co-developer of the Unix operating system.

Lemma 7.11. For each set, L ∈ RAT(M) there is a nondeterministic finiteM-automatonA with L = L(A).

Proof: Let 1 ∈ M be the neutral element. For every rational set L, we construct an automaton AL with the following invariants:

□

The construction is by induction on the number of nested operations union, product and star, which are necessary to obtain L. If L = {u1, . . . , un} is finite, then AL is the following automaton:

If L = K ∪ K' for K, K' ∈ RAT(M) and if the automata AK and AK' are constructed already, then AL is given by

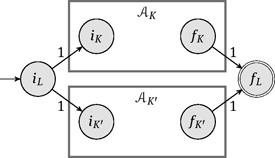
This means that we take the disjoint union of AK and AK ' including all transitions and add a new initial state i L and a new final state fL. If L = KK', then AL is defined by

For L = K ∗ we finally define

The last construction for L = K ∗ is correct because in AK there is no incoming arc to i k and there is no outgoing arc leaving fK. Thus, L = L(AL) in all cases.

□

Next, we show that for all automata one can assume that there are no ε-transition of the form (p, 1, q). Such a transition allows a spontaneous switch from state p to q. Accordingly, the procedure in the following proof is often referred to as elimination of ε-transitions.

Lemma 7.12. Let A be a nondeterministic finite M-automaton and Σ a given generating set of M. Then there exists an equivalent nondeterministic finite M-automatonBaccepting L with labels from Σ and only one initial state.

Proof: We transform A = (Q, δ, I, F) by a sequence of substitutions into the automaton B = (Q' , δ' , {i}, F) having the desired properties. Since δ is finite, we can assume Q to be finite, too. Let u ∈ M (Σ ∪ {1}) and let (p, u, q) ∈ δ be a transition. Then there exists a1, . . . , an ∈ Σ with u = a1 ⋅⋅ ⋅ an and n ≥ 2. We add new states q1, . . . , qn−1 to Q and remove the transition (p, u, q) from δ. Then we add the transitions

In this manner, we proceed with every transition whose label is in M (Σ ∪ {1}). Next, we add a new state i and transitions { (i, 1, q0) | q0 ∈ I }. From now on, the state i is the only initial state. By introducing more transitions with label 1, we can assume that whenever (p, 1, q) and (q, 1, r) are transitions, then (p, 1, r) is a transition, too. We define the set of final states as

This does not change the accepted set. Therefore, we have now obtained an automaton B' = (Q' , δ,' {i}, F), which is equivalent to A and whose labels all are in Σ ∪ {1}.

We now remove all transitions (p, 1, q) ∈ δ' and add the transitions

instead. This yields the automaton B. Each run in B has a canonical counterpart in B. Now let r = q0u1q1 ⋅⋅ ⋅ unqn be an accepting run of B' with ui ∈ Σ∪{1}. Since we added all transitive 1-transitions to B' ,we can assume that two consecutive labels ui and ui+1 never are both 1. By construction of F, we can assume that un ≠ 1 (except for n = 0). So if ui = 1, then i < n and ui+1 ≠ 1. Therefore, in the case ui = 1, we can always replace the partial run qi−1uiqiui+1qi+1 of r by qi−1ui+1qi+1 and obtain an accepting run in B. This shows L(B) = L(B'). Together with L(B') = L(A), the proof of the lemma is complete.