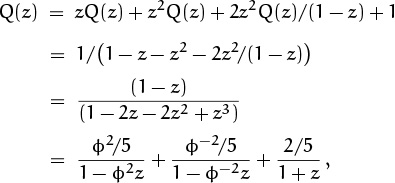6.1 2314, 2431, 3241, 1342, 3124, 4132, 4213, 1423, 2143, 3412, 4321.

6.2 , because every such function partitions its domain into k nonempty subsets, and there are m^k ways to assign function values for each partition. (Summing over k gives a combinatorial proof of (6.10).)

6.3 Now d_k+1 ≤ (center of gravity) – = 1 – + (d₁ + · · · + d_k)/k. This recurrence is like (6.55) but with 1 – in place of 1; hence the optimum solution is d_k+1 = (1 – )H_k. This is unbounded as long as < 1.

6.4 . (Similarly .)

6.5 U_n(x, y) is equal to

and the first sum is

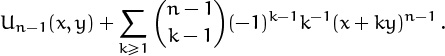
The remaining k^–1 can be absorbed, and we have

This proves (6.75). Let R_n(x, y) = x^–nU_n(x, y); then R₀(x, y) = 0 and R_n(x, y) = R_n–1(x, y)+1/n+y/x, hence R_n(x, y) = H_n+ny/x. (Incidentally, the original sum U_n = U_n(n, –1) doesn’t lead to a recurrence such as this; therefore the more general sum, which detaches x from its dependence on n, is easier to solve inductively than its special case. This is another instructive example where a strong induction hypothesis makes the difference between success and failure.)

The Fibonacci recurrence is additive, but the rabbits are multiplying.

6.6 Each pair of babies bb present at the end of a month becomes a pair of adults aa at the end of the next month; and each pair aa becomes an aa and a bb. Thus each bb behaves like a drone in the bee tree and each aa behaves like a queen, except that the bee tree goes backward in time while the rabbits are going forward. There are F_n+1 pairs of rabbits after n months; F_n of them are adults and F_n–1 are babies. (This is the context in which Fibonacci originally introduced his numbers.)

6.7 (a) Set k = 1 – n and apply (6.107). (b) Set m = 1 and k = n – 1 and apply (6.128).

6.8 55 + 8 + 2 becomes 89 + 13 + 3 = 105; the true value is 104.60736.

That “true value” is the length of 65 international miles, but the international mile is actually only .999998 as big as a U. S. statute mile. There are exactly 6336 kilometers in 3937 U. S. statute miles; the Fibonacci method converts 3937 to 6370.

6.9 21. (We go from F_n to F_n+2 when the units are squared. The true answer is about 20.72.)

6.10 The partial quotients a₀, a₁, a₂, . . . are all equal to 1, because ϕ = 1 + 1/ϕ. (The Stern–Brocot representation is therefore RLRLRLRLRL . . . .)

6.11 ; see (6.11).

6.12 This is a consequence of (6.31) and its dual in Table 264.

6.13 The two formulas are equivalent, by exercise 12. We can use induction. Or we can observe that zⁿDⁿ applied to f(z) = z^x gives xⁿz^x while ϑⁿ applied to the same function gives xⁿz^x; therefore the sequence ϑ⁰, ϑ¹, ϑ², . . . must relate to z⁰D⁰, z¹D¹, z²D², . . . as x⁰, x¹, x², . . . relates to x⁰, x¹, x², . . . .

6.14 We have

because (n + 1)x = (k + 1)(x + k – n) + (n – k)(x + k + 1). (It suffices to verify the latter identity when k = 0, k = –1, and k = n.)

6.15 Since , we have the general formula

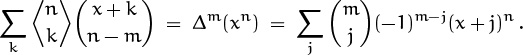
Set x = 0 and appeal to (6.19).

6.16 ; this sum is always finite.

6.17 (a) (b) (c)

6.18 This is equivalent to (6.3) or (6.8).

6.19 Use Table 272.

6.20

6.21 The hinted number is a sum of fractions with odd denominators, so it has the form a/b with b odd. (Incidentally, Bertrand’s postulate implies that b_n is also divisible by at least one odd prime, whenever n > 2.)

6.22 |z/k(k + z)| ≤ 2|z|/k² when k > 2|z|, so the sum is well defined when the denominators are not zero. If z = n we have , which approaches H_n as m → ∞. (The quantity H_z–1 – γ is often called the psi function ψ(z).)

6.23 z/(e^z + 1) = z/(e^z – 1) – 2z/(e^2z – 1) = ∑_n≥0(1 – 2ⁿ)B_nzⁿ/n!.

6.24 When n is odd, T_n(x) is a polynomial in x², hence its coefficients are multiplied by even numbers when we form the derivative and compute T_n+1(x) by (6.95). (In fact we can prove more: The Bernoulli number B_2n always has 2 to the first power in its denominator, by exercise 54; hence 2^2n–k \T_2n+1 ⇔ 2^k\(n + 1). The odd positive integers (n + 1)T_2n+1/2²ⁿ are called Genocchi numbers 1, 1, 3, 17, 155, 2073, . . . , after Genocchi [145].)

(Of course Euler knew the Genocchi numbers long before Genocchi was born; see [110], Volume 2, Chapter 7, §181.)

6.25 100n – nH_n < 100(n – 1) – (n – 1)H_n–1 ⇔ H_n–1 > 99. (The least such n is approximately e^99–γ, while he finishes at N ≈ e^100–γ, about e times as long. So he is getting closer during the final 63% of his journey.)

6.26 Let u(k) = H_k–1 and Δv(k) = 1/k, so that u(k) = v(k). Then we have .

6.27 Observe that when m > n we have gcd(F_m, F_n) = gcd(F_m–n, F_n) by (6.108). This yields a proof by induction.

6.28 (a) Q_n = α(L_n – F_n)/2 + βF_n. (The solution can also be written .

6.29 When k = 0 the identity is (6.133). When k = 1 it is, essentially,

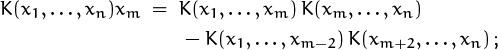
in Morse code terms, the second product on the right subtracts out the cases where the first product has intersecting dashes. When k > 1, an induction on k suffices, using both (6.127) and (6.132). (The identity is also true when one or more of the subscripts on K become –1, if we adopt the convention that K_–1 = 0. When multiplication is not commutative, Euler’s identity remains valid for k = n – 1 if we write it in the form

For example, we obtain the somewhat surprising noncommutative factorizations

(abc + a + c)(1 + ba) = (ab + 1)(cba + a + c)

from the case m = 0, n = 3.)

6.30 The derivative of K(x₁, . . . , x_n) with respect to x_m is

K(x₁, . . . , x_m–1) K(x_m+1, . . . , x_n),

and the second derivative is zero; hence the answer is

K(x₁, . . . , x_n) + K(x₁, . . . , x_m–1) K(x_m+1, . . . , x_n)y.

6.31 Since , we have . These coefficients, incidentally, satisfy the recurrence

.

6.32 and , both of which appear in Table 265.

6.33 If n > 0, we have , by (6.71); , by (6.19).

6.34 We have ; and in general is given by (6.38) for all integers n.

6.35 Let n be the least integer > 1/ such that H_n > H_n–1.

6.36 Now d_k+1 = (100+(1+d₁)+· · ·+(1+d_k))/(100+k), and the solution is d_k+1 = H_k+100 – H₁₀₁ + 1 for k ≥ 1. This exceeds 2 when k ≥ 176.

6.37 The sum (by parts) is . The infinite sum is therefore ln m. (It follows that

because ν_m(k) = (m – 1) ∑_j≥1(k mod m^j)/m^j.)

6.38 . (By parts, using (5.16).)

6.39 Write it as ∑_1≤j≤n j^–1 ∑_j≤k≤n H_k and sum first on k via (6.67), to get

6.40 If 6n – 1 is prime, the numerator of

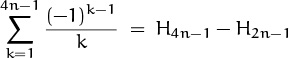
is divisible by 6n – 1, because the sum is

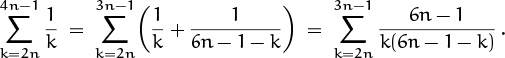
Similarly if 6n + 1 is prime, the numerator of is a multiple of 6n + 1. For 1987 we sum up to k = 1324.

6.41 , hence we have S_n+1 + . The answer is F_n+2.

6.42 F_n.

6.43 Set in Σ_n≥0 F_nzⁿ = z/(1 – z – z²) to get . The sum is a repeating decimal with period length 44:

0.11235 95505 61797 75280 89887 64044 94382 02247 19101 12359 55+.

6.44 Replace (m, k) by (–m, –k) or (k, –m) or (–k, m), if necessary, so that m ≥ k ≥ 0. The result is clear if m = k. If m > k, we can replace (m, k) by (m – k, m) and use induction.

6.45 X_n = A(n)α+B(n)β+C(n)γ+D(n)δ, where B(n) = F_n, A(n) = F_n–1, A(n) + B(n) – D(n) = 1, and B(n) – C(n) + 3D(n) = n.

6.46 ϕ/2 and ϕ^–1/2. Let u = cos 72° and v = cos 36°; then u = 2v² – 1 and v = 1–2 sin² 18° = 1–2u². Hence u+v = 2(u+v)(v–u), and 4v²–2v–1 = 0. We can pursue this investigation to find the five complex fifth roots of unity:

“Let p be any old prime.”
(See [171], p. 419.)

6.47 , and the even powers of cancel out. Now let p be an odd prime. Then except when k = (p–1)/2, and except when k = 0 or k = (p – 1)/2; hence F_p ≡ 5^(p–1)/2 and 2F_p+1 ≡ 1 + 5^(p–1)/2 (mod p). It can be shown that 5^(p–1)/2 ≡ 1 when p has the form 10k ± 1, and 5^(p–1)/2 ≡ –1 when p has the form 10k ± 3.

6.48 Let K_i,j = K_j–i+1(x_i, . . . , x_j). Using (6.133) repeatedly, both sides expand to (K_1,m–2(x_m–1 + x_m+1) + K_1,m–3)K_m+2,n + K_1,m–2K_m+3,n.

6.49 Set in (6.146); the partial quotients are 0, 2^F₀, 2^F₁, 2^F₂, . . .  . (Knuth [206] noted that this number is transcendental.)

6.50 (a) f(n) is even ⇔ 3n. (b) If the binary representation of n is (1^a₁ 0^a₂ . . . 1^a_m–1 0^a_m )₂, where m is even, we have f(n)=K(a₁, a₂, . . . , a_m–1).

6.51 (a) Combinatorial proof: The arrangements of {1, 2, . . . , p} into k subsets or cycles are divided into “orbits” of 1 or p arrangements each, if we add 1 to each element modulo p. For example,

We get an orbit of size 1 only when this transformation takes an arrangement into itself; but then k = 1 or k = p. Alternatively, there’s an algebraic proof: We have x^p ≡ x^p + x¹ and x^p ≡ x^p – x (mod p), since Fermat’s theorem tells us that x^p – x is divisible by (x – 0)(x – 1) . . . (x – (p–1)).

(b) This result follows from (a) and Wilson’s theorem; or we can use .

(c) We have for 3 ≤ k ≤ p, then for 4 ≤ k ≤ p, etc. (Similarly, we have .)

(d) . But , so

is a multiple of p². (This is called Wolstenholme’s theorem.)

(Attention, computer programmers: Here’s an interesting condition to test, for as many primes as you can.)

6.52 (a) Observe that , where . (b) Working mod 5 we have H_r = 0, 1, 4, 1, 0 for 0 ≤ r ≤ 4. Thus the first solution is n = 4. By part (a) we know that 5a_n ⇒ 5a_n/5; so the next possible range is n = 20 + r, 0 ≤ r ≤ 4, when we have H_n = . The numerator of , like the numerator of H₄, is divisible by 25. Hence the only solutions in this range are n = 20 and n = 24. The next possible range is n = 100 + r; now , which is plus a fraction whose numerator is a multiple of 5. If , where m is an integer, the harmonic number H_100+r will have a numerator divisible by 5 if and only if m + H_r ≡ 0 (mod 5); hence m must be ≡ 0, 1, or 4. Working modulo 5 we find ; hence there are no solutions for 100 ≤ n ≤ 104. Similarly there are none for 120 ≤ n ≤ 124; we have found all three solutions.

(By exercise 6.51(d), we always have p²a_p–1, pa_p²–p, and pa_p²–1, if p is any prime ≥ 5. The argument just given shows that these are the only solutions to pa_n if and only if there are no solutions to p^–2H_p–1 + H_r ≡ 0 (mod p) for 0 ≤ r < p. The latter condition holds not only for p = 5 but also for p = 13, 17, 23, 41, and 67—perhaps for infinitely many primes. The numerator of H_n is divisible by 3 only when n = 2, 7, and 22; it is divisible by 7 only when n = 6, 42, 48, 295, 299, 337, 341, 2096, 2390, 14675, 16731, 16735, and 102728. See the answer to exercise 92.)

6.53 Summation by parts yields

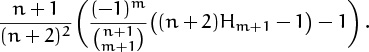
(The numerators of Bernoulli numbers played an important role in early studies of Fermat’s Last Theorem; see Ribenboim [308].)

6.54 (a) If m ≥ p we have S_m(p) ≡ S_m–(p–1)(p) (mod p), since k^p–1 ≡ 1 when 1 ≤ k < p. Also S_p–1(p) ≡ p – 1 ≡ –1. If 0 < m < p – 1, we can write

(b) The condition in the hint implies that the denominator of I_2n is not divisible by any prime p; hence I_2n must be an integer. To prove the hint, we may assume that n>1. Then

is an integer, by (6.78), (6.84), and part (a). So we want to verify that none of the fractions has a denominator divisible by p. The denominator of isn’t divisible by p, since B_k has no p² in its denominator (by induction); and the denominator of p^2n–k–1/(2n – k + 1) isn’t divisible by p, since 2n – k + 1 < p^2n–k when k ≤ 2n–2; QED. (The numbers I_2n are tabulated in [224]. Hermite calculated them through I₁₈ in 1875 [184]. It turns out that I₂ = I₄ = I₆ = I₈ = I₁₀ = I₁₂ = 1; hence there is actually a “simple” pattern to the Bernoulli numbers displayed in the text, including . But the numbers I_2n don’t seem to have any memorable features when 2n > 12. For example, , and 86579 is prime.)

(c) The numbers 2–1 and 3–1 always divide 2n. If n is prime, the only divisors of 2n are 1, 2, n, and 2n, so the denominator of B_2n for prime n > 2 will be 6 unless 2n+1 is also prime. In the latter case we can try 4n+3, 8n+7, . . . , until we eventually hit a nonprime (since n divides 2^n–1n + 2^n–1 – 1). (This proof does not need the more difficult, but true, theorem that there are infinitely many primes of the form 6k + 1.) The denominator of B_2n can be 6 also when n has nonprime values, such as 49.

6.55 The stated sum is , by Vandermonde’s convolution. To get (6.70), differentiate and set x = 0.

6.56 First replace kⁿ⁺¹ by ((k – m) + m)ⁿ⁺¹ and expand in powers of k – m; simplifications occur as in the derivation of (6.72). If m > n or m < 0, the answer is . Otherwise we need to take the limit of (5.41) minus the term for k = m, as x → –m; the answer comes to .

6.57 First prove by induction that the nth row contains at most three distinct values A_n ≥ B_n ≥ C_n; if n is even they occur in the cyclic order [C_n, B_n, A_n, B_n, C_n], while if n is odd they occur in the cyclic order [C_n, B_n, A_n, A_n, B_n]. Also

A2n+1 =	A2n + B2n ;	A2n =	2A2n–1 ;
B2n+1 =	B2n + C2n ;	B2n =	A2n–1 + B2n–1 ;
C2n+1 =	2C2n ;	C2n =	B2n–1 + B2n–1 .

It follows that Q_n = A_n – C_n = F_n+1. (See exercise 5.75 for wraparound binomial coefficients of order 3.)

6.58 (a) . (Square Binet’s formula (6.123) and sum on n, then combine terms so that ϕ and disappear.) (b) Similarly,

It follows that . (The corresponding recurrence for mth powers involves the Fibonomial coefficients of exercise 86; it was discovered by Jarden and Motzkin [194].)

6.59 Let m be fixed. We can prove by induction on n that it is, in fact, possible to find such an x with the additional condition x ≢ 2 (mod 4). If x is such a solution, we can move up to a solution modulo 3ⁿ⁺¹ because

either x or x + 8·3^n–1 or x + 16·3^n–1 will do the job.

6.60 F₁ + 1, F₂ + 1, F₃ + 1, F₄ – 1, and F₆ – 1 are the only cases. Otherwise the Lucas numbers of exercise 28 arise in the factorizations

(We have F_m+n – (–1)ⁿF_m–n = L_mF_n in general.)

6.61 1/F_2m = F_m–1/F_m – F_2m–1/F_2m when m is even and positive. The second sum is 5/4 – F_3·2ⁿ–1/F_3·2ⁿ, for n ≥ 1.

6.62 (a) and . Incidentally, we also have and . (b) A table of small values reveals that

(c) B_n/A_n+1 – B_n–1/A_n = 1/(F_2n+1 + 1) because and . Notice that B_n/A_n+1 = (F_n/F_n+1)[n even]+(L_n/L_n+1)[n odd]. (d) Similarly, . This quantity can also be expressed as (5F_n/L_n+1)[n even] + (L_n/F_n+1)[n odd].

6.63 (a) . There are with π_n = n and with π_n < n. (b) . Each permutation ρ₁ . . . ρ_n–1 of {1, . . . , n–1} leads to n permutations π₁π₂ . . . π_n = ρ₁ . . . ρ_j–1 n ρ_j+1 . . . ρ_n–1ρ_j. If ρ₁ . . . ρ_n–1 has k excedances, there are k+1 values of j that yield k excedances in π₁π₂ . . . π_n; the remaining n–1–k values yield k+1. Hence the total number of ways to get k excedances in π₁π₂ . . . π_n is .

6.64 The denominator of , by the proof in exercise 5.72. The denominator of is the same, by (6.44), because and is even for k > 0.

6.65 This is equivalent to saying that is the probability that we have x₁ + · · · + x_n = k, when x₁, . . . , x_n are independent random numbers uniformly distributed between 0 and 1. Let y_j = (x₁ + · · · + x_j) mod 1. Then y₁, . . . , y_n are independently and uniformly distributed, and x₁ + · · · + x_n is the number of descents in the y’s. The permutation of the y’s is random, and the probability of k descents is the same as the probability of k ascents.

6.66 2ⁿ⁺¹(2ⁿ⁺¹ – 1)B_n+1/(n + 1), if n > 0. (See (7.56) and (6.92); the desired numbers are essentially the coefficients of 1 – tanh z.)

6.67 It is by (6.3) and (6.40). Now use (6.34). (This identity has a combinatorial interpretation [59].)

6.68 We have the general formula

analogous to (6.38). When m = 2 this equals

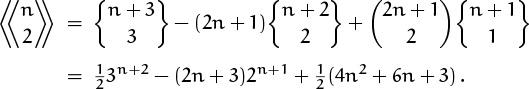
6.69 . (It would be nice to automate the derivation of formulas such as this.)

6.70 1/k – 1/(k + z) = z/k² – z²/k³ + · · · , which converges when |z| < 1.

6.71 Note that . If we find f(z)/z! + γ = H_z.

6.72 For tan z, we can use tan z = cot z – 2 cot 2z (which is equivalent to the identity of exercise 23). Also has the power series ∑_n≥0(–1)^n–1(4ⁿ – 2)B_2nz²ⁿ/(2n)!; and

because and .

6.73 cot(z + π) = cot z and ; hence the identity is equivalent to

which follows by induction from the case n = 1. The stated limit follows since z cot z → 1 as z → 0. It can be shown that term-by-term passage to the limit is justified, hence (6.88) is valid. (Incidentally, the general formula

is also true. It can be proved from (6.88), or from

which is equivalent to the partial fraction expansion of 1/(zⁿ – 1).)

6.74 Since tan 2z + sec 2z = (sin z + cos z)/(cos z – sin z), setting x = 1 in (6.94) gives T_n(1) = 2ⁿE_n, where 1/cos z = ∑_n≥0 E_2nz²ⁿ/(2n)!. (The coefficients E_n are called Euler numbers in combinatorics, not to be confused with the Eulerian numbers . We have E₀, E₁, E₂, . . . = 1, 1, 1, 2, 5, 16, 61, 272, 1385, 7936, 50521, . . . . Numerical analysts define Euler numbers differently: Their E_n is (–1)^n/2E_n[n even] in the notation above.)

6.75 Let G(w, z) = sin z/ cos(w+z) and H(w, z) = cos z/ cos(w+z), and let G(w, z) + H(w, z) = ∑_m,n E_m,nw^mzⁿ/m! n!. Then the equations G(w, 0) = 0 and imply that E_m,0 = 0 when m is odd, E_m,n+1 = E_m+1,n + E_m,n when m + n is even; the equations H(0, z) = 1 and imply that E_0,n = [n = 0] when n is even, E_m+1,n = E_m,n+1+E_m,n when m+n is odd. Consequently the nth row below the apex of the triangle contains the numbers E_n,0, E_n–1,1, . . . , E_0,n. At the left, E_n,0 is the secant number E_n [n even]; at the right, E_0,n = T_n + [n = 0].

6.76 Let A_n denote the sum. Looking ahead to equation (7.49), we see that . Therefore, by exercise 23 or 72,

A_n = (2ⁿ⁺¹ – 4ⁿ⁺¹)B_n+1/(n + 1) = (–1)^(n+1)/2T_n + [n = 0].

6.77 This follows by induction on m, using the recurrence in exercise 18. It can also be proved from (6.50), using the fact that

The latter equation, incidentally, is equivalent to

6.78 If p(x) is any polynomial of degree ≤ n, we have

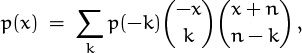
because this equation holds for x = 0, –1, . . . , –n. The stated identity is the special case where p(x) = xσ_n(x) and x = 1. Incidentally, we obtain a simpler expression for Bernoulli numbers in terms of Stirling numbers by setting k = 1 in (6.99):

6.79 Sam Loyd [256, pages 288 and 378] gave the construction

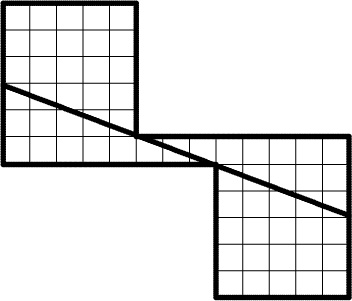
and claimed to have invented (but not published) the 64 = 65 arrangement in 1858. (Similar paradoxes go back at least to the eighteenth century, but Loyd found better ways to present them.)

He also published it in the Brooklyn Daily Eagle (28 August 1904), 39; (11 September 1904), 37.

6.80 We expect A_m/A_m–1 ≈ ϕ, so we try A_m–1 = 618034 + r and A_m–2 = 381966–r. Then A_m–3 = 236068+2r, etc., and we find A_m–18 = 144–2584r, A_m–19 = 154 + 4181r. Hence r = 0, x = 154, y = 144, m = 20.

6.81 If P(F_n+1, F_n) = 0 for infinitely many even values of n, then P(x, y) is divisible by U(x, y) – 1, where U(x, y) = x² – xy – y². For if t is the total degree of P, we can write

Then

and we have by taking the limit as n → ∞. Hence Q(x, y) is a multiple of U(x, y), say A(x, y)U(x, y). But U(F_n+1, F_n) = (–1)ⁿ and n is even, so P₀(x, y) = P(x, y) – (U(x, y) – 1)A(x, y) is another polynomial such that P₀(F_n+1, F_n) = 0. The total degree of P₀ is less than t, so P₀ is a multiple of U – 1 by induction on t.

Similarly, P(x, y) is divisible by U(x, y) + 1 if P(F_n+1, F_n) = 0 for infinitely many odd values of n. A combination of these two facts gives the desired necessary and sufficient condition: P(x, y) is divisible by U(x, y)² – 1.

6.82 First add the digits without carrying, getting digits 0, 1, and 2. Then use the two carry rules

always applying the leftmost applicable carry. This process terminates because the binary value obtained by reading (b_m . . . b₂)_F as (b_m . . . b₂)₂ increases whenever a carry is performed. But a carry might propagate to the right of the “Fibonacci point”; for example, (1)_F +(1)_F becomes (10.01)_F. Such rightward propagation extends at most two positions; and those two digit positions can be zeroed again by using the text’s “add 1” algorithm if necessary.

Incidentally, there’s a corresponding “multiplication” operation on nonnegative integers: If m = F_j1 +· · ·+F_jq and n = F_k1 +· · ·+F_kr in the Fibonacci number system, let , by analogy with multiplication of binary numbers. (This definition implies that when m and n are large, although 1 ο n ≈ ϕ²n.) Fibonacci addition leads to a proof of the associative law l ο (m ο n) = (l ο m) ο n.

Exercise: m ο n = mn + (m+1)/ϕn + m (n+1)/ϕ.

6.83 Yes; for example, we can take

A0 =	331635635998274737472200656430763 ;
A1 =	1510028911088401971189590305498785 .

The resulting sequence has the property that A_n is divisible by (but unequal to) p_k when n mod m_k = r_k, where the numbers (p_k, m_k, r_k) have the following 18 respective values:

(3, 4, 1)		(2, 3, 2)		(5, 5, 1)
(7, 8, 3)		(17, 9, 4)		(11, 10, 2)
(47, 16, 7)		(19, 18, 10)		(61, 15, 3)
(2207, 32, 15)		(53, 27, 16)		(31, 30, 24)
(1087, 64, 31)		(109, 27, 7)		(41, 20, 10)
(4481, 64, 63)		(5779, 54, 52)		(2521, 60, 60)

One of these triples applies to every integer n; for example, the six triples in the first column cover every odd value of n, and the middle column covers all even n that are not divisible by 6. The remainder of the proof is based on the fact that A_m+n = A_mF_n–1 + A_m+1F_n, together with the congruences

A₀ ≡ F_mk–rk mod p_k ,

A₁ ≡ F_mk–rk+1 mod p_k ,

for each of the triples (p_k, m_k, r_k). (An improved solution, in which A₀ and A₁ are numbers of “only” 17 digits each, is also possible [218].)

6.84 The sequences of exercise 62 satisfy A_–m = A_m, B_–m = –B_m, and

A_mA_n = A_m+n + A_m–n ;

A_mB_n = B_m+n – B_m–n ;

B_mB_n = A_m+n – A_m–n .

Let f_k = B_mk/A_mk+l and g_k = A_mk/B_mk+l, where . Then f_k+1 – f_k = A_lB_m/(A_2mk+n + A_m) and g_k – g_k+1 = A_lB_m/(A_2mk+n – A_m); hence we have

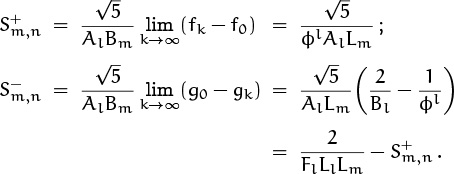
6.85 The property holds if and only if N has one of the seven forms 5^k, 2·5^k, 4·5^k, 3^j·5^k, 6·5^k, 7·5^k, 14·5^k.

6.86 For any positive integer m, let r(m) be the smallest index j such that C_j is divisible by m; if no such j exists, let r(m) = ∞. Then C_n is divisible by m if and only if gcd(C_n, C_r(m)) is divisible by m if and only if C_gcd(n,r(m)) is divisible by m if and only if gcd(n, r(m)) = r(m) if and only if n is divisible by r(m).

(Conversely, the gcd condition is easily seen to be implied by the condition that the sequence C₁, C₂, . . . has a function r(m), possibly infinite, such that C_n is divisible by m if and only if n is divisible by r(m).)

Now let Π(n) = C₁C₂ . . . C_n, so that

If p is prime, the number of times p divides Π(n) is f_p(n) = ∑_k≥1 n/r(p^k), since n/p^k is the number of elements {C₁, . . . , C_n} that are divisible by p^k. Therefore f_p(m + n) ≥ f_p(m) + f_p(n) for all p, and is an integer.

6.87 The matrix product is

This relates to products of L and R as in (6.137), because we have

The determinant is K_n(x₁, . . . , x_n); the more general tridiagonal determinant

satisfies the recurrence D_n = x_nD_n–1 – y_nD_n–2.

6.88 Let α^–1 = a₀ + 1/(a₁ + 1/(a₂ + · · · )) be the continued fraction representation of α^–1. Then we have

where

A proof analogous to the text’s proof of (6.146) uses a generalization of Zeckendorf’s theorem (Fraenkel [129, §4]). If z = 1/b, where b is an integer ≥ 2, this gives the continued fraction representation of the transcendental number (b – 1) ∑_n≥1 b^–nα, as in exercise 49.

6.89 Let p = K(0, a₁, a₂, . . . , a_m), so that p/n is the mth convergent to the continued fraction. Then α = p/n + (–1)^m/nq, where q = K(a₁, . . . , a_m, β) and β > 1. The points {kα} for 0 ≤ k < n can therefore be written

where π₁ . . . π_n–1 is a permutation of {1, . . . , n – 1}. Let f(v) be the number of such points < v; then f(v) and vn both increase by 1 when v increases from k/n to (k + 1)/n, except when k = 0 or k = n – 1, so they never differ by 2 or more.

6.90 By (6.139) and (6.136), we want to maximize K(a₁, . . . , a_m) over all sequences of positive integers whose sum is ≤ n + 1. The maximum occurs when all the a’s are 1, for if j ≥ 1 and a ≥ 1 we have

Kj+k+1(1, . . . , 1, a + 1, b1, . . . , bk)
=	Kj+k+1(1, . . . , 1, a, b1, . . . , bk) + Kj(1, . . . , 1) Kk(b1, . . . , bk)
≤	Kj+k+1(1, . . . , 1, a, b1, . . . , bk) + Kj+k(1, . . . , 1, a, b1, . . . , bk)
=	Kj+k+2(1, . . . , 1, a, b1, . . . , bk).

(Motzkin and Straus [278] show how to solve more general maximization problems on continuants.)

6.91 A candidate for the case n mod appears in [213, §6], although it may be best to multiply the integers discussed there by some constant involving . An elegant and more convincing proposal has been put forward by Philippe Flajolet and Helmut Prodinger in SIAM Journal on Discrete Mathematics 12 (1999), 155–159.

6.92 (a) David Boyd has shown that there are only finitely many solutions for all p < 500, except perhaps p = 83, 127, 397. (b) The behavior of b_n is quite strange: We have b_n = lcm(1, . . . , n) for 968 ≤ n ≤ 1066; on the other hand, b₆₀₀ = lcm(1, . . . , 600)/(3³ · 5² · 43). Andrew Odlyzko observes that p divides lcm(1, . . . , n)/b_n if and only if kp^m ≤ n < (k + 1)p^m for some m ≥ 1 and some k < p such that p divides the numerator of H_k. Therefore infinitely many such n exist if it can be shown, for example, that almost all primes have only one such value of k (namely k = p – 1).

Another reason to remember 1066?

6.93 (Brent [38] found the surprisingly large partial quotient 1568705 in e^γ, but this seems to be just a coincidence. For example, Gosper has found even larger partial quotients in π: The 453,294th is 12996958 and the 11,504,931st is 878783625.)

6.94 Consider the generating function , which equals ∑_k (wF(α′ + β′ + γ′, α′ + β′, α′) + zF(α + γ, α + β, α))^k(1), where F(a, b, c) is the differential operator a + bϑ_w + cϑ_z.

6.95 An elegant solution to this research problem has been found by Manuel Kauers, Journal of Symbolic Computation 42 (2007), 948–970.

Kauers succeeded even though Stirling numbers are not “holonomic” in the sense of [383].

7.1 Substitute z⁴ for and z for in the generating function, getting 1/(1 – z⁴ – z²). This is like the generating function for T, but with z replaced by z². Therefore the answer is zero if m is odd, otherwise F_m/2+1.

7.2 G(z) = 1/(1 – 2z) + 1/(1 – 3z); Ĝ(z) = e^2z + e^3z.

7.3 Set z = 1/10 in the generating function, getting ln .

7.4 Divide P(z) by Q(z), getting a quotient T(z) and a remainder P₀(z) whose degree is less than the degree of Q. The coefficients of T(z) must be added to the coefficients [zⁿ] P₀(z)/Q(z) for small n. (This is the polynomial T(z) in (7.28).)

7.5 This is the convolution of (1 + z²)^r with (1 + z)^r, so

S(z) = (1 + z + z² + z³)^r.

Incidentally, no simple form is known for the coefficients of this generating function; hence the stated sum probably has no simple closed form. (We can use generating functions to obtain negative results as well as positive ones.)

7.6 Let the solution to g₀ = α, g₁ = β, g_n = g_n–1 + 2g_n–2 + (–1)ⁿγ be g_n = A(n)α + B(n)β + C(n)γ. The function 2ⁿ works when α = 1, β = 2, γ = 0; the function (–1)ⁿ works when α = 1, β = –1, γ = 0; the function (–1)ⁿn works when α = 0, β = –1, γ = 3. Hence A(n) + 2B(n) = 2ⁿ, A(n) – B(n) = (–1)ⁿ, and –B(n) + 3C(n) = (–1)ⁿn.

7.7 G(z) = (z/(1 – z)²)G(z) + 1, hence

we have g_n = F_2n + [n = 0].

I bet that the controversial “fan of order zero” does have one spanning tree.

7.8 Differentiate (1 – z)^–x–1 twice with respect to x, obtaining

Now set x = m.

7.9

7.10 The identity implies that .

7.11 (a) C(z) = A(z)B(z²)/(1 – z). (b) zB′(z) = A(2z)e^z, hence . (c) A(z) = B(z)/(1 – z)^r+1, hence B(z) = (1 – z)^r+1A(z) and we have .

7.12 C_n. The numbers in the upper row correspond to the positions of +1’s in a sequence of +1’s and –1’s that defines a “mountain range”; the numbers in the lower row correspond to the positions of –1’s. For example, the given array corresponds to

7.13 Extend the sequence periodically (let x_m+k = x_k) and define s_n = x₁ + · · · + x_n. We have s_m = l, s_2m = 2l, etc. There must be a largest index k_j such that s_kj = j, s_kj+m = l + j, etc. These indices k₁, . . . , k_l (mod m) specify the cyclic shifts in question.

For example, in the sequence –2, 1, –1, 0, 1, 1, –1, 1, 1, 1 with m = 10 and l = 2 we have k₁ = 17, k₂ = 24.

7.14 Ĝ(z) = –2zĜ(z) + Ĝ(z)² + z (be careful about the final term!) leads via the quadratic formula to

Hence g_2n+1 = 0 and g_2n = (–1)ⁿ(2n)! C_n–1, for all n > 0.

7.15 There are partitions with k other objects in the subset containing n+1. Hence . The solution to this differential equation is , and c = –1 since . (We can also get this result by summing (7.49) on m, since .)

7.16 One way is to take the logarithm of

B(z) = 1/((1 – z)^a₁ (1 – z²)^a₂ (1 – z³)^a₃ (1 – z⁴)^a₄ . . .),

then use the formula for ln and interchange the order of summation.

7.17 This follows since . There’s also a formula that goes in the other direction:

7.18 (a) (b) –ζ′(z); (c) ζ(z)/ζ(2z). Every positive integer is uniquely representable as m²q, where q is squarefree.

7.19 If n > 0, the coefficient [zⁿ] exp(x ln F(z)) is a polynomial of degree n in x that’s a multiple of x. The first convolution formula comes from equating coefficients of zⁿ in F(z)^xF(z)^y = F(z)^x+y. The second comes from equating coefficients of z^n–1 in F′(z)F(z)^x–1F(z)^y = F′(z)F(z)^x+y–1, because we have

(Further convolutions follow by taking ∂/∂x, as in (7.43).)

Still more is true, as shown in [221]: We have

for arbitrary x, y, and t. In fact, xf_n(x + tn)/(x + tn) is the sequence of polynomials for the coefficients of F_t(z)^x, where

F_t(z) = F(zF_t(z)^t) .

(We saw special cases in (5.59) and (6.52).)

7.20 Let G(z) = ∑_n≥0 g_nzⁿ. Then

for all k, l ≥ 0, if we regard g_n = 0 for n < 0. Hence if P₀(z), . . . , P_m(z) are polynomials, not all zero, having maximum degree d, then there are polynomials p₀(n), . . . , p_m+d(n) such that

Therefore a differentiably finite G(z) implies that

The converse is similar. (One consequence is that G(z) is differentiably finite if and only if the corresponding egf, Ĝ(z), is differentiably finite.)

7.21 This is the problem of giving change with denominations 10 and 20, so G(z) = 1/(1 – z¹⁰)(1 – z²⁰) = (z¹⁰), where (z) = 1/(1 – z)(1 – z²). (a) The partial fraction decomposition of (z) is , so . Setting n = 50 yields 26 ways to make the payment. (b) (z) = (1 + z)/(1 – z²)² = (1 + z)(1 + 2z² + 3z⁴ + · · · ), so [zⁿ] (z) = n/2 + 1. (Compare this with the value N_n = n/5 + 1 in the text’s coin-changing problem. The bank robber’s problem is equivalent to the problem of making change with pennies and tuppences.)

This slow method of finding the answer is just the cashier’s way of stalling until the police come.

The USA has two-cent pieces, but they haven’t been minted since 1873.

7.22 Each polygon has a “base” (the line segment at the bottom). If A and B are triangulated polygons, let AB be the result of pasting the base of A to the upper left diagonal of , and pasting the base of B to the upper right diagonal. Thus, for example,

(The polygons might need to be warped a bit and/or banged into shape.) Every triangulation arises in this way, because the base line is part of a unique triangle and there are triangulated polygons A and B at its left and right.

Replacing each triangle by z gives a power series in which the coefficient of zⁿ is the number of triangulations with n triangles, namely the number of ways to decompose an (n + 2)-gon into triangles. Since P = 1 + zP², this is the generating function for Catalan numbers C₀ + C₁z + C₂z² + · · · ; the number of ways to triangulate an n-gon is .

7.23 Let a_n be the stated number, and b_n the number of ways with a 2×1×1 notch missing at the top. By considering the possible patterns visible on the top surface, we have

a_n = 2a_n–1 + 4b_n–1 + a_n–2 + [n = 0] ;
b_n = a_n–1 + b_n–1 .

Hence the generating functions satisfy A = 2zA + 4zB + z²A + 1, B = zA + zB, and we have

This formula relates to the problem of 3 × n domino tilings; we have a_n = , which is rounded to the nearest integer.

“Curiously, a_2n is equal to , the square of the number of ways to tile a 3 × 2n rectangle with dominoes; and .”

—I. Kaplansky

7.24 n∑_k1+···+k_m=n k₁ · . . . · k_m/m = F_2n+1 + F_2n–1 – 2. (Consider the coefficient , where G(z) = z/(1 – z)².)

7.25 The generating function is P(z)/(1 – z^m), where P(z) = z + 2z² + · · · + (m – 1)z^m–1 = ((m – 1)z^m+1 – mz^m + z)/(1 – z)². The denominator is Q(z) = 1 – z^m = (1 – ω⁰z)(1 – ω¹z) . . . (1 – ω^m–1z). By the rational expansion theorem for distinct roots, we obtain

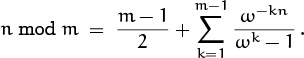
7.26 leads to as in equation (7.61).

7.27 Each oriented cycle pattern begins with or or a 2 × k cycle (for some k ≥ 2) oriented in one of two ways. Hence

Q_n = Q_n–1 + Q_n–2 + 2Q_n–2 + 2Q_n–3 + · · · + 2Q₀

for n ≥ 2; Q₀ = Q₁ = 1. The generating function is therefore

and .

7.28 In general if A(z) = (1 + z + · · · + z^m–1)B(z), we have A_r + A_r+m + A_r+2m + · · · = B(1) for 0 ≤ r < m. In this case m = 10 and B(z) = (1 + z + · · · + z⁹)(1 + z² + z⁴ + z⁶ + z⁸)(1 + z⁵).

7.29 , so the answer is .

7.30 , by exercise 5.39.

7.31 The dgf is ζ(z)²/ζ(z–1); hence we find g(n) is the product of (k+1–kp) over all prime powers p^k that exactly divide n.

7.32 We may assume that each b_k ≥ 0. A set of arithmetic progressions forms an exact cover if and only if

Subtract z^b_m/(1 – z^a_m) from both sides and set z = e^2πi/a_m. The left side is infinite, and the right side will be finite unless a_m–1 = a_m.

7.33 (–1)^n–m+1[n > m]/(n – m).

7.34 We can also write . In general, if

we have G_n = z₁G_n–1 + z₂G_n–2 + · · · + z_rG_n–r + [n = 0], and the generating function is 1/(1 – z₁w – z₂w² – · · · – z_rw^r). In the stated special case the answer is 1/(1 – w – z^mw^m+1). (See (5.74) for the case m = 1.)

7.35 (a) . (b) by (7.50) and (6.58). Another way to do part (b) is to use the rule with .

7.36

7.37 (a) The amazing identity a_2n = a_2n+1 = b_n holds in the table

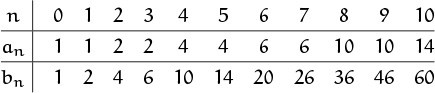
(b) A(z) = 1/((1 – z)(1 – z²)(1 – z⁴)(1 – z⁸) . . .). (c) B(z) = A(z)/(1 – z), and we want to show that A(z) = (1 + z)B(z²). This follows from A(z) = A(z²)/(1 – z).

7.38 (1 – wz)M(w, z) = ∑_m,n≥1(min(m, n) – min(m–1, n–1))w^mzⁿ = ∑_m,n≥1 w^mzⁿ = wz/(1 – w)(1 – z). In general,

7.39 The answers to the hint are

respectively. Therefore: (a) We want the coefficient of z^m in the product (1 + z)(1 + 2z) . . . (1 + nz). This is the reflection of , so it is and the answer is . (b) The coefficient of z^m in 1/((1– z)(1 – 2z)...(1 – nz)) is by (7.47).

7.40 The egf for nF_n–1 – F_n is where . The egf for n¡ is e^–z/(1 – z). The product is

We have . So the answer is (–1)ⁿF_n.

7.41 The number of up-down permutations with the largest element n in position 2k is . Similarly, the number of up-down permutations with the smallest element 1 in position 2k + 1 is , because down-up permutations and up-down permutations are equally numerous. Summing over all possibilities gives

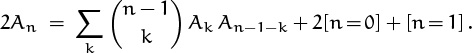
The egf  therefore satisfies 2Â′(z) = Â(z)² +1 and Â(0) = 1; the given function solves this differential equation. (Consequently A_n is the Euler number E_n of exercise 6.74, namely a secant number when n is even, a tangent number when n is odd.)

7.42 Let a_n be the number of Martian DNA strings that don’t end with c or e; let b_n be the number that do. Then

and the total number is [zⁿ](1 + z)/(1 – 4z – z²) = F_3n+2.

7.43 By (5.45), g_n = ΔⁿĠ(0). The nth difference of a product can be written

and . Therefore we find

This is a sum over all trinomial coefficients; it can be put into the more symmetric form

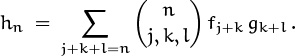
The empty set is pointless.

7.44 Each partition into k nonempty subsets can be ordered in k! ways, so b_k = k!. Thus . And this is the geometric series ∑_k≥0 e^kz/2^k+1, hence a_k = 1/2^k+1. Finally, c_k = 2^k; consider all permutations when the x’s are distinct, change each ‘>’ between subscripts to ‘<’ and allow each ‘<’ between subscripts to become either ‘<’ or ‘=’. (For example, the permutation x₁x₃x₂ produces x₁ < x₃ < x₂ and x₁ = x₃ < x₂, because 1 < 3 > 2.)

7.45 This sum is ∑_n≥1 r(n)/n², where r(n) is the number of ways to write n as a product of two relatively prime factors. If n is divisible by t distinct primes, r(n) = 2^t. Hence r(n)/n² is multiplicative and the sum is

7.46 Let . Then S_n = S_n–1 + αS_n–3 + [n = 0], and the generating function is 1/(1 – z – αz³). When , the hint tells us that this has a nice factorization . The general expansion theorem now tells us that , and the remaining constant c turns out to be .

7.47 The Stern–Brocot representation of is R(LR²)^∞, because

The fractions are ; they eventually have the cyclic pattern

7.48 We have g₀ = 0, and if g₁ = m the generating function satisfies

Hence G(z) = P(z)/(az² + bz + c)(1 – z) for some polynomial P(z). Let ρ₁ and ρ₂ be the roots of cz² + bz + a, with |ρ₁| ≥ |ρ₂|. If b² – 4ac ≤ 0 then |ρ₁|² = ρ₁ρ₂ = a/c is rational, contradicting the fact that approaches . Hence ; and this implies that a = –c, b = –2c, . The generating function now takes the form

where r = d/c. Since g₂ is an integer, r is an integer. We also have

and this can hold only if r = –1, because alternates in sign as it approaches zero. Hence (a, b, c, d) = ±(1, 2, –1, 1). Now we find , which is between 0 and 1 only if 0 ≤ m ≤ 2. Each of these values actually gives a solution; the sequences g_n are 0, 0, 1, 3, 8, . . . , 0, 1, 3, 8, 20, . . . , and 0, 2, 5, 13, 32, . . . .

7.49 (a) The denominator of is 1 – 2z – z²; hence a_n = 2a_n–1 + a_n–2 for n ≥ 2. (b) True because a_n is even and . (c) Let

We would like b_n to be odd for all n > 0, and . Working as in part (a), we find b₀ = 2, b₁ = p, and for n ≥ 2. One satisfactory solution has p = 3 and q = 17.

7.50 Extending the multiplication idea of exercise 22, we have

Replace each n-gon by z^n–2. This substitution behaves properly under multiplication, because the pasting operation takes an m-gon and an n-gon into an (m + n – 2)-gon. Thus the generating function is

and the quadratic formula gives . The coefficient of z^n–2 in this power series is the number of ways to put nonoverlapping diagonals into a convex n-gon. These coefficients apparently have no closed form in terms of other quantities that we have discussed in this book, but their asymptotic behavior is known [207, exercise 2.2.1–12].

Incidentally, if each n-gon in Q is replaced by wz^n–2 we get

a formula in which the coefficient of w^mz^n–2 is the number of ways to divide an n-gon into m polygons by nonintersecting diagonals.

Give me Legendre polynomials and I’ll give you a closed form.

7.51 The key first step is to observe that the square of the number of ways is the number of cycle patterns of a certain kind, generalizing exercise 27. These can be enumerated by evaluating the determinant of a matrix whose eigenvalues are not difficult to determine. When m = 3 and n = 4, the fact that cos 36° = ϕ/2 is helpful (exercise 6.46).

7.52 The first few cases are p₀(y) = 1, p₁(y) = y, p₂(y) = y² + y, p₃(y) = y³ + 3y² + 3y. Let p_n(y) = q_2n(x) where y = x(1 – x); we seek a generating function that defines q_2n+1(x) in a convenient way. One such function is ∑_n q_n(x)zⁿ/n! = 2e^ixz/(e^iz + 1), from which it follows that q_n(x) = iⁿE_n(x), where E_n(x) is called an Euler polynomial. We have , so Euler polynomials are analogous to Bernoulli polynomials, and they have factors analogous to those in (6.98). By exercise 6.23 we have ; this polynomial has integer coefficients by exercise 6.54. Hence q_2n(x), whose coefficients have denominators that are powers of 2, must have integer coefficients. Hence p_n(y) has integer coefficients. Finally, the relation shows that

and it follows that the ’s are positive. (A similar proof shows that the related quantity (–1)ⁿ(2n + 2)E_2n+1(x)/(2x – 1) has positive integer coefficients, when expressed as an nth degree polynomial in y.) It can be shown that is the Genocchi number (–1)^n–1(2²ⁿ⁺¹ – 2)B_2n (see exercise 6.24), and that , etc.

7.53 It is P_{(1+V4n+1+V4n+3)/6}. Thus, for example, T₂₀ = P₁₂ = 210; T₂₈₅ = P₁₆₅ = 40755.

7.54 Let E_k be the operation on power series that sets all coefficients to zero except those of zⁿ where n mod m = k. The stated construction is equivalent to the operation

E₀ S E₀ S (E₀ + E₁) S ... S (E₀ + E₁ + · · · + E_m–1)

applied to 1/(1 – z), where S means “multiply by 1/(1 – z).” There are m! terms

E₀ S E_k1 S E_k2 S ... S E_km

where 0 ≤ k_j < j, and every such term evaluates to z^rm/(1 – z^m)^m+1 if r is the number of places where k_j < k_j+1. Exactly terms have a given value of r, so the coefficient of z^mn is by (6.37). (The fact that operation E_k can be expressed with complex roots of unity seems to be of no help in this problem.)

7.55 Suppose that P₀(z)F(z) + · · · + P_m(z)F^(m)(z) = Q₀(z)G(z) + · · · + Q_n(z)G⁽ⁿ⁾(z) = 0, where P_m(z) and Q_n(z) are nonzero. (a) Let H(z) = F(z) + G(z). Then there are rational functions R_k,l(z) for 0 ≤ l < m + n such that H^(k)(z) = R_k,0(z)F⁽⁰⁾(z) + · · · + R_k,m–1(z)F^(m–1)(z) + R_k,m(z)G⁽⁰⁾(z) + · · · + R_k,m+n–1(z)G^(n–1)(z). The m + n + 1 vectors (R_k,0(z), . . . , R_k,m+n–1(z)) are linearly dependent in the (m + n)-dimensional vector space whose components are rational functions; hence there are rational functions S_l(z), not all zero, such that S₀(z)H⁽⁰⁾(z) + · · · + S_m+n(z)H^(m+n)(z) = 0. (b) Similarly, let H(z) = F(z)G(z). There are rational R_k,l(z) for 0 ≤ l < mn with , hence S₀(z)H⁽⁰⁾(z) + · · · + S_mn(z)H^(mn)(z) = 0 for some rational S_l(z), not all zero. (A similar proof shows that if f_n and g_n are polynomially recursive, so are f_n + g_n and f_ng_n. Incidentally, there is no similar result for quotients; for example, cos z is differentiably finite, but 1/cos z is not.)

7.56 Euler [113] showed that this number is also , and he gave the formula . He also discovered a “memorable failure of induction” while examining these numbers: Although 3t_n – t_n+1 is equal to F_n–1(F_n–1 + 1) for 0 ≤ n ≤ 8, this empirical law mysteriously breaks down when n is 9 or more! George Andrews [12] has explained the mystery by showing that the sum ∑_k[z^n+10k] (1 + z + z²)ⁿ can be expressed as a closed form in terms of Fibonacci numbers.

H. S. Wilf observes that [zⁿ] (a + bz + cz²)ⁿ= [zⁿ] 1/f(z), where (see [373, page 159]), and it follows that the coefficients satisfy

(n + 1)A_n+1 – (2n + 1)bA_n + n(b² – 4ac)A_n–1 = 0.

The algorithm of Petkovšek [291] can be used to prove that this recurrence has a closed form solution as a finite sum of hypergeometric terms if and only if abc(b² – 4ac) = 0. Therefore in particular, the middle trinomial coefficients have no such closed form. The next step is presumably to extend this result to a larger class of closed forms (including harmonic numbers and/or Stirling numbers, for example).

Give me Legendre polynomials and I’ll give you a closed form.

7.57 (Paul Erdős repeatedly offered $500 for a solution to this problem.)