Chapter | one
Music Acoustic Sound
CHAPTER OUTLINE
“Sound” is an English-based word. “Audio” is derived from Latin, and refers to things that are related to hearing. Sound does not necessarily have to be audible. Infrasound and ultrasound, which are below and above the normal range of human hearing, respectively, are examples of inaudible sounds.
In English, we tend to use the terms “sound” and “audio” indiscriminately. When discussing acoustical topics in this book, we will be dealing with “sound,” and that is where we will begin.
WHAT IS SOUND?
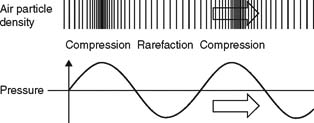
Sound is normally understood to mean elastic molecular oscillations in air or other media such as water, iron, or concrete. These oscillations result in pressure variations that are of such a magnitude that they can be sensed by human hearing.
However, sound can also be converted to, for example, variations in the electrical current in a conductor, or magnetic variations on an audio tape, or a sequence of numeric values. We call these forms intermediate formats, because we later convert them into acoustic sound.
SPEED OF SOUND
Sound propagates by an oscillating solid body setting the particles next to it in motion, and those next to them, and so on. Sound thus spreads with a certain propagation velocity. This is called the speed of sound, which varies depending on the medium.
FIGURE 1.1 Sound (in air) can be defined as variations in air pressure.
The speed of sound (c) in a medium is normally specified in meters per second [m/s] or feet per second [ft/s]. In the air the speed of sound is dependent on the temperature:
In air, at 0°C or 32°F, the speed of sound is 331.4 m/s or 1086 ft/s (1193 km/t or 740.5 mph).
In air, at 20°C or 68°F, the speed of sound is 343.54 m/s or 1126 ft/s (1237 km/t or 767.7 mph).
However, as a rule 340 m/s or 1130 ft/s are used as approximations for the speed of sound for general purposes. Thus in applied audio technology, one often encounters the following values:
34 cm/ms (Sound travels about 34 cm each millisecond.)
3 ms/m (Sound takes roughly 3 ms to travel 1 meter.)
or
1 ft/ms (Sound travels about 1 ft each millisecond.)
FREQUENCY
Frequency (f) is a measure of the number of oscillations or cycles per second, and is specified in hertz (abbreviated as Hz).
where
f = frequency [Hz]
T = period [s]
A frequency of 1 Hz = 1 cycle per second.Afrequency of 1000 Hz = 1000 cycles per second (1000 Hz is normally expressed as 1 kiloHertz, abbreviated as 1 kHz).
The nominal audible frequency range of human hearing comprises frequencies from 20 Hz to 20 kHz. This range is called the audio frequency range.
WAVELENGTH
The wavelength is the distance a single oscillation takes to complete in a given medium. The wavelength is thus dependent on the frequency and the speed of sound in the medium concerned.
It can be expressed in the following manner:
where
λ = wavelength [m]
c = speed of sound [m/s]
f = frequency [Hz]
or
λ = wavelength [ft]
c = speed of sound [ft/s]
f = frequency [Hz]
This relationship shows that the audio spectrum in air contains wavelengths ranging from approximately 17 m at 20 Hz down to 17 mm at 20 kHz or from approximately 55 ft at 20 Hz down to 0.055 ft at 20 kHz. This is referred to as the “wave theory boundary area,” because the sound wavelengths are in the same order as the dimensions of the rooms and equipment that are used for recording and listening (microphones, loudspeakers, etc.).
This boundary area has an influence on everything from the acoustics of rooms to the directional patterns of loudspeakers, as well as the frequency response of microphones.
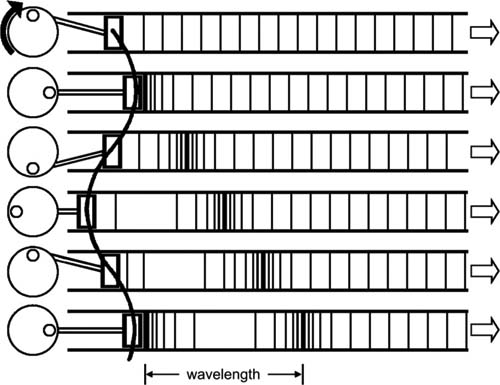
If the concept ofwavelength is a little difficult to comprehend, it helps to imagine the sound radiating from a sound source as pressure variations generated by the source being carried away on a conveyer at a given fixed speed (the speed of sound). If one “freezes” this image the distance between two maxima is the wavelength of that frequency. If the frequency is increased, one period of that frequency is finished in less time and the travelled distance gets shorter, hence a shorter wavelength.
TABLE 1.1 Wavelengths in Air. In this Calculation the Speed of Sound is 344 m/s or 1126 ft/s. Wavelengths in Air. In this Calculation the Speed of Sound is 344 m/s or 1126 ft/s.
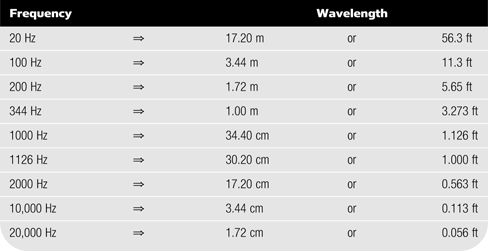
FIGURE 1.2 A sound source regarded as a piston. Pressure generated at the piston is transported away at a constant speed. Hence, the wavelength of a given frequency is the distance between two identical points in adjacent cycles.
SOUND PRESSURE
Air surrounds us. We call the static pressure of air the barometric pressure. Sound pressure is defined as the difference between the instantaneous pressure and the static pressure.
Pressure is measured in pascals (abbreviated Pa). One pascal is defined as 1 N/m2 (newton per square meter).
The sound pressure can be regarded as a modulation of the static pressure. The greater the variations in sound pressure, the stronger the perception of the sound, i.e., loudness.
The weakest audible sound at 1 kHz has a sound pressure of approximately 20 μPa (20 micro-pascal = 20·10-6 Pa), whereas the ear’s threshold of pain lies at a sound pressure of around 20 Pa. The weakest audible sound and the threshold of pain thus differ by a factor of one million.
CONVERSION RELATIONSHIPS
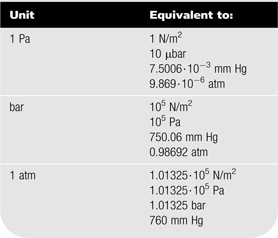
The pascal (Pa) is a unit of the SI system (International System of Units). Other units are still seen in practice, for example on older data sheets for microphones, where the bar unit is used.
SOUND POWER
Sound is a form of energy, hence the concept of sound power.
Sound power is the sound energy transferred during a period divided by the period of time concerned. In a travelling plane wave with a sound pressure of 20 mPa, the power that passes through an area of 1 m2 placed perpendicular to the direction of travel is
TABLE 1.2 Conversion Between Pa, Bar, and Atmosphere (Atm).
1 pW (one pico-watt = 10-12 watt).
This value is used as a reference when specifying a sound power level. For a sound pressure of 20 Pa, the power is 1 W.
Sound power, for example from a loudspeaker or from a machine, is measured in practice either in a reverberation chamber (a room with highly reflective surfaces) or by performing a large number of sound pressure measurements around the object; these measurements subsequently are used to calculate the power.
SOUND INTENSITY
Sound intensity is an expression of power per unit of area. For a flow of sound energy that is propagating in a specific direction, the intensity is the power that is transferred through an area perpendicular to the direction of travel, divided by the area.
For a travelling plane wave with a sound pressure of 20 mPa, this intensity is 1 pW/m2.
Sound intensity has a directional component. In practice, the sound intensity from a sound source is measured using a sound intensity probe consisting of two transducers (pressure microphones) at a well-defined distance. By looking at the phase of the radiated sound, among other things, the direction of the sound can be determined.
SOUND FIELDS
Spherical Sound Field
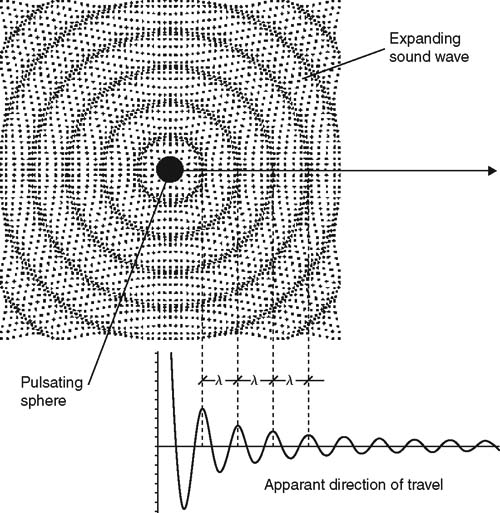
When sound is radiated from a point source, the intensity decreases with distance. It can be compared with a balloon when being filled with air: the bigger the diameter, the thinner the rubber wall at a given area on the circumference. The balloon consists of a certain amount of rubber that has to cover a still larger volume. There is a quadratic relation between the radius and the area. Doubling the radius enlarges the area by four.
FIGURE 1.3 SounD radiating from a point source.
The intensity falls with distance according to:
where
I = sound intensity
d = distance
This is called the inverse square law.
Therefore, the sound pressure falls according to:
where
P = sound pressure
d = distance
Thus, doubling the distance halves the sound pressure. In dB, the sound level drops 6 dB when doubling the distance.
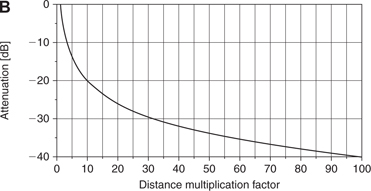
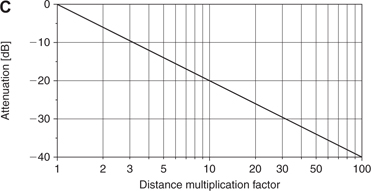
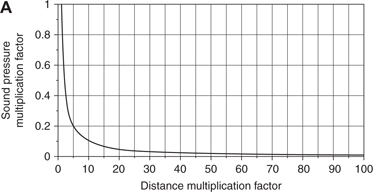
FIGURE 1.4 Point source: Three different ways to express the relation between sound pressure and distance. A: Sound pressure (expressed as a multiplication factor) vs. distance (expressed as a multiplication factor). Example: Moving 10 times the initial distance (meters, feet, yards,…) away from the sound source changes the sound pressure by a factor of 0.1. B: Attenuation of sound pressure (expressed in dB) vs. distance (expressed as a multiplication factor). Example: Moving 10 times the initial distance away from the sound source reduces the sound pressure by 20 dB. C: Sound pressure (expressed in dB) vs. distance (expressed as a multiplication factor on a logarithmic scale). The values are the same as in B. However, the curve here is a straight line.
Cylindrical Sound Field
An (infinite) line source generates a cylindrical sound field.
The intensity falls with distance according to:
where
I = sound pressure
d = distance
Hence the sound pressure falls according to:
where
I = sound pressure
d = distance
Thus, doubling the distance reduces the sound pressure by √2. In dB, the sound level drops 3 dB when doubling the distance.
Some loudspeaker designs are pronounced line sources, typically formed by an array of speaker units. In practical audio engineering these loudspeakers may act as line sources within a limited distance and frequency range. In the far field the practical (finite) line array is always considered to be a point source.
Plane Sound Field
In a plane sound field the sound does not attenuate as the intensity of the sound field is kept constant in the direction of the propagation. In other words, the attenuation is 0 dB. However, infinite plane sound sources do not exist. In real life an approximation of the plane sound field can be experienced far away from a point source where a limited sector of a spherical sound field can be regarded as plane. Another approximation exists very close to a large loudspeaker membrane or a vibrating wall. (For instance, if a microphone is placed 1 cm from a 12-inch loudspeaker unit and then moved 1 cm further away it does not really change the sound level.)