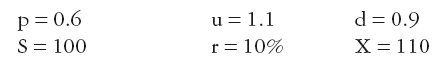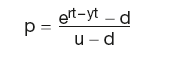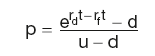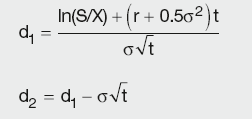9
Motivation behind option trading
Option contract specifications
Option contract risks and benefits
Option value sensitivities – ‘option Greeks’
Option pricing: practical implementation
MOTIVATION BEHIND OPTION TRADING
An option gives the buyer the right but not the obligation to enter at a future date into a transaction specified today. The buyer will obviously use it to his advantage and only exercise the option if it is beneficial compared to the prevailing market conditions at expiry. In the event of exercise the option seller must fulfil his obligation at loss. To accept this risk he charges a premium payable up-front. Clearly all the buyer can lose is the cost of the premium if the option expires unexercised, whilst the seller has an unlimited exposure. Hence his view of the market must be opposite.
Options are derivative instruments, i.e. their price is derived from the value of an underlying security. They are valuable tools used for hedging and speculation.
Hedgers use options as a form of insurance. If they believe that the price of an asset they will require in the future will increase they buy an option that allows them to fix the purchase price today. If their expectations prove to be correct, they will exercise the option. However, if they can transact more cheaply in the market, they will simply abandon the option. Similarly, an option to sell an asset in the future at a price agreed today protects the option buyer against the price decrease. Should the prices rise, the option would be abandoned and the asset sold more profitably in the market.
Speculators take their positions purely to make a profit from expected market moves. They neither require, nor own an underlying security and aim to close out their position by reversing the option contract prior to expiry. Alternatively, they can sell options with the view that they will not be exercised, expecting to keep the premium.
OPTION CONTRACT SPECIFICATIONS
The option contract gives the buyer or holder the right but not the obligation to transact with the option seller or writer in the future. At the inception, the following is agreed:
- Expiry date is the date when the option can be exercised. There are two types of options: American option, which can be exercised at any point until expiry; or European option, which can be exercised only at the expiry date.
- Option type specifies whether the option is the right to buy (call option) or the right to sell (put option). These can be viewed from the holder’s or writer’s point of view.
Long call gives the right to buy an underlying.
Long put gives the right to sell an underlying.
Short call is an obligation to buy an underlying (if the option is exercised).
Short put is an obligation to sell an underlying (if the option is exercised). - Underlying is an asset (interest rate, equity, commodity etc.) from which the option derives value.
- Strike price or strike rate is chosen by the option buyer as the price at which the future transaction can take place. Its value is not derived from the forward market and depends on the amount of protection/speculation the buyer is willing to undertake.
At-the-money (ATM) option has a strike price equal to the forward price.
In-the-money (ITM) option has a strike price that is more favourable than the forward price.
Out-of-the-money (OTM) option has a strike price that is less advantageous than the forward price. - Intrinsic value of an option is the difference between the strike price and the current market price of an ITM option. For an OTM option it is zero rather than negative, as an option without value would simply lapse, rather than incur costs to the holder.
- Time value is the built in cost of the premium that allows for uncertainty of exercise. It is greater for longer-dated options and reduces to zero at expiry.
- Option premium is the cost of the option contract. It is based on its intrinsic value and time value.
TYPES OF OPTION CONTRACTS
Options can be traded at both recognised exchanges and OTC. The pros and cons of both markets are the same as for other financial securities. The exchange-traded options are limited in the range of underlying securities, whilst more ‘exotic’ products, tailor-made to specific client requirements, are traded OTC. Some examples of exchange-traded options are:
Interest rate options where the underlying is an interest rate. They are used as protection against adverse movements in interest rates, but unlike futures and FRAs they also allow for potential profit if rates move in the buyer’s favour. On exercise only the difference between the interest rates is settled, based on the specified notional amount.
Cross-currency options have an exchange rate as an underlying. However, they implicitly derive their value from the interest rates in the two exchanged currencies. As above, on exercise only the difference between the rates is settled, based on the specified notional amount.
Stock options derive their value from the price of a single stock. On exercise, depending on exchange specifications, the stock can be bought/sold or the difference in price settled.
Equity index options are based on a specific equity index. They are always settled on price difference.
Commodity options have an actual commodity as an underlying (wheat, coffee, crude oil etc.), thus the delivery is usually expected, or implied in pricing (includes cost of storage, shipment etc.).
Some more exotic options traded OTC are:
Swap options or swaptions allow the holder to enter into a swap on exercise. They derive their value from the implicit swap underlying.
Binary option pays a fixed amount if the option is in the money at expiry. The underlying can be any security.
Spread option pays the difference between a pair of underlying asset prices.
Option types
As mentioned above, there are four possible option positions:
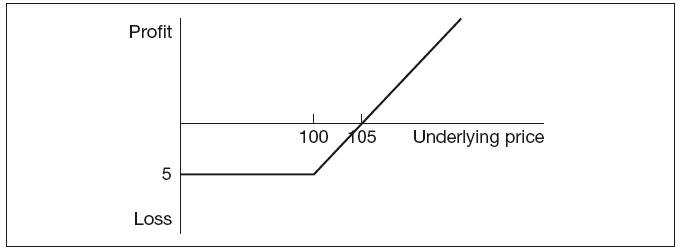
Long call is the right to buy an underlying at a specific price. For example, a long call option with the strike price 100 and premium 5 would be exercised if the market price at expiry is equal or greater than 100. The price achieved will have to incorporate the premium paid, thus the position will only turn into profit above 105. The payout profile would resemble that shown in Figure 9.1.
Figure 9.1 Long call option payout profile
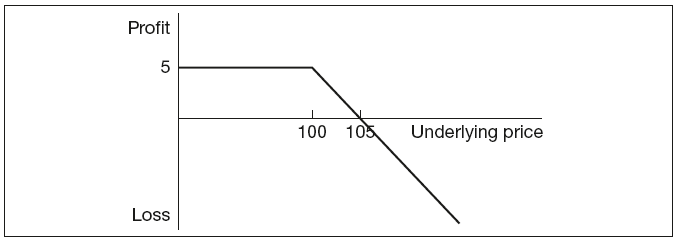
Short call is the above scenario from the point of view of the option seller. He receives the premium of 5 up-front. If the underlying price is below 100 at expiry, the option will be abandoned and the full premium will be realised as profit. As the price rises, the position crosses over into loss, as shown in Figure 9.2.
Figure 9.2 Short call option payout profile
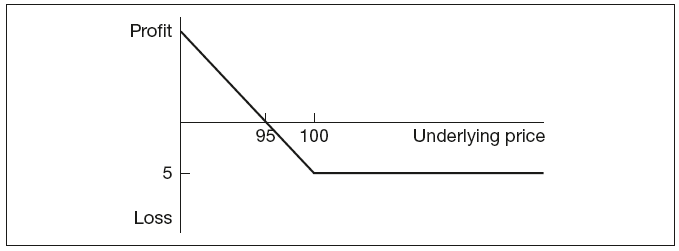
Long put is the right to sell an underlying at a specific price. For example, a long put option with the strike price 100 and premium 5 would be exercised if the market price at expiry is equal to or lower than 100. The price achieved will have to incorporate the premium paid, thus the position will only turn into profit below 95. The payout profile would resemble that shown in Figure 9.3.
Figure 9.3 Long put option payout profile
Short put is the above scenario from the point of view of the option seller. He receives the premium of 5 up-front. If the underlying price is above 100 at expiry, the option will be abandoned and the full premium will be realised as profit. As the price falls, the position crosses over into a loss, as shown in Figure 9.4.
Figure 9.4 Short put option payout profile
There are many option strategies that can be based on the above four basic trades. They are graphically presented in Appendix 1.
OPTION CONTRACT RISKS AND BENEFITS
As the only cashflow at inception of the option contract is the premium, it is an ‘off-balance sheet’ instrument, which makes it an attractive instrument for those with limited credit lines. More importantly, the potential profit/loss can be multifold of the premium (a concept called ‘gearing’), making options one of the riskiest derivative securities. For example, if a long call with strike 100 and premium 5 is exercised when the underlying is 120, it realises 15 in premium, which is 300 per cent of the funds required for the trade. If we owned the underlying, the same price increase would realise only 20 per cent of the initial value. The opposite is also true; if the underlying at expiry was worth 80, the option holder would lose 100 per cent of the premium, whilst the asset holder would lose only 20 per cent.
From the diagrams above we can also see that all the option buyer can lose is the cost of the premium. However, the seller of the call has unlimited exposure. In the case of the short put position the loss is limited to strike – premium, as the asset price can never fall below zero. This one-sided exposure implies that the option writers have very strong views on the future market movements, otherwise they would not enter into the transaction.
IDEAS BEHIND OPTION PRICING
The amount of premium the option seller requires is based on the probability that the option will be exercised and the expected loss this would incur. It is akin to travel insurance, whereby the premium is lower for a two-day city break than for two weeks of paragliding, as the latter has a much higher probability of resulting in a serious accident. Hence the option pricing takes into account:
The strike price – a more favourable strike price to the buyer implies a higher premium, as the option will have a greater intrinsic value. The time value will depend on the time to expiry. This relationship is not linear; at inception the option loses very little time value with each passing day, but as the expiry approaches the decay increases dramatically.
Volatility – the underlying price fluctuation. The more volatile the underlying the more time value the option will have and consequently the higher the premium will be. This is because more volatile assets have a greater chance to expire ITM. As the options writer is pricing options on an asset to be bought/sold in the future, the volatility relevant to the valuation is future volatility, something that cannot possibly be known.
Hence it is estimated assuming certain behaviour of an asset, using a probability distribution. This is the range of possible values the underlying can take with the probability of each outcome assigned. For example, an asset that has a current value of 100 cannot be worth less than zero and cannot reach infinity. It is also more likely to remain in the 80–120 range than to be priced at 50 or 200 and so on. In practice, traders assume that percentage changes in asset prices are normally distributed, whilst asset prices are log-normally distributed. Types of distributions and other aspects of probability and statistics relevant to option pricing are covered in Chapter 13.
Since future volatility can only be estimated, the alternatives are:
Historic volatility, taken from the analysis of historic market data.
Implied volatility, calculated from current option prices by working ‘backwards’ to see which value of volatility would result in the market price.
Neither measure actually predicts the future volatility, as historic data may be completely irrelevant to the events that will influence price fluctuations in the future, whilst implied volatility is simply other market practitioners’ view of the future.
Option maturity – the more time the underlying price has to fluctuate, the more likely it is that the option will be exercised; hence the premium increases with maturity.
Interest rates – the relationship between interest rates and premiums is not unique, it depends on the type of the option and the underlying.
For physically settled options call premiums rise (as the option seller has to finance the purchase of the underlying at higher rates) and put premiums fall (it is the option buyer who incurs the cost and expects to be compensated by a reduced premium).
For options on futures with up-front premiums call and put premiums fall, as the option writer can invest the profit at higher rates.
For options on futures that are margined call and put premiums are unaffected, as the rate fluctuation will be incorporated into daily margins.
For bond options, swaptions and other options with interest rate derivatives as underlying, and exotic options in particular, the relationship between the premium and interest rate is more complex.
The above variables are incorporated into the option pricing methodology. There are two main approaches, analytical and numerical, which are described later.
PUT–CALL PARITY
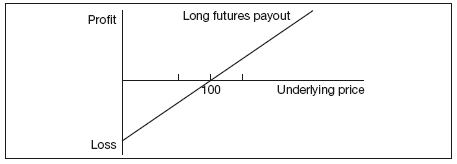
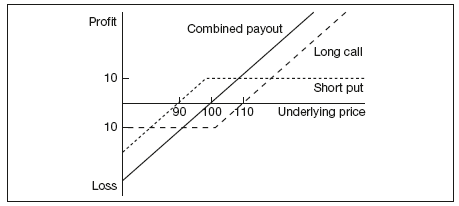
Put–call parity describes the relationship between the prices of a put option, call option and an underlying asset. If one counterparty purchases a future at 100, their payout profile would be as presented in Figure 9.5. If another counterparty buys a call with strike 100 and premium of 10 and simultaneously sells a put with the identical strike and premium, their payout profiles at exercise would be as given in Figure 9.6.
Figure 9.5 Long futures payout profile
Figure 9.6 Synthetic long futures combined payout profile
It can be seen that the combination of a long call and short put generates the same payout profile as a long futures position. This, in fact, is a common trading strategy known as synthetic long futures. It follows that if we know the futures and call prices, the put premium can be derived from the formula:
Calculation Summary: Put–call parity
C – P = S – K
where:
C and P are the call and put premiums
S is the futures price
K is the exercise price/option strike.
This concept has very important implications for option pricing. As will be seen in the following sections, the analytical model for option pricing gives the value of a call option; hence using the above expression, the value of the corresponding put option can be calculated. Alternatively, it can be used for hedging purposes to generate a zero net position. If a counterparty is long futures, to hedge they would sell a call and buy a put. For short futures positions a reverse hedge would be constructed.
This basic put–call parity formula can be extended to various types of futures contracts:
Calculation Summary: Put–call parity
Physically settled options:
C – P = S – Ke–rt
where:
r is the continuously compounded interest rate
t is time to expiry expressed as
.
Options on dividend-paying stocks:
where D is the present value of expected dividend.
Options on stock index (dividend yield continuous):
where d is the continuously compounded dividend yield.
Cross-currency options:
Calculation Summary
where:
f is the continuously compounded foreign currency interest rate
S is the spot exchange rate.
Options on futures with up-front premiums:
C − P = S − K
Options on futures with margined premiums:
OPTION VALUE SENSITIVITIES – ‘OPTION GREEKS’
As stated earlier, the option premium is the function of five parameters:
- Price of underlying
- Strike/exercise price
- Volatility of underlying price
- Time to expiry
- Interest rates.
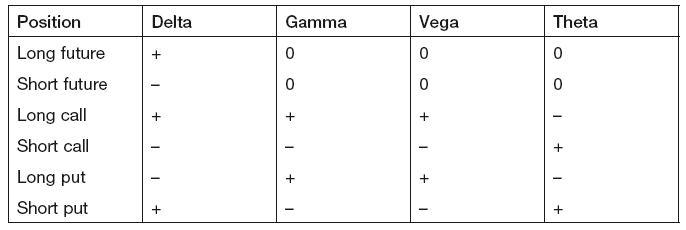
The sensitivity of the theoretical option value to each factor is given a Greek letter, hence the commonly used term ‘Option Greeks’, summarised in Table 9.1.
Table 9.1 Option price sensitivities – ‘Greeks’
| Options sensitivity to | Named as |
|---|---|
| Underlying | Delta |
| Changes in delta | Gamma |
| Volatility | Vega or kappa |
| Time decay | Theta |
| Interest rates | Rho |
Delta
Delta is the option sensitivity to the value of the underlying. Its value represents by how much the option price changes for 1 unit change in the price of underlying. However, it can be interpreted in other, more practical ways:
- Delta is the rate of change of the option value with respect to underlying security. In other words, delta of 0.25 implies that for a price change of 1, the option value would change by 0.25.
- Delta is the theoretical number of futures required to hedge the option position. If delta is 0.25, a trader would need four futures to replicate the option’s exposure.
- Delta is also a probability exercise. The option with 0.25 delta theoretically has a 25 per cent chance of expiring ITM.
The relationship between option contract and the underlying determines the sign of delta.
The holder of a long call benefits from a rise in the underlying value, i.e. the value of the call increases with the price, implying positive delta. The position of the call writer is the reverse.
The holder of a long put is adversely affected by the increase in the underlying price, as the value of put (and the probability of exercise) decreases, hence delta is negative. The opposite is true for the short put. This can be summarised as shown in Table 9.2.
Table 9.2 Sign of option delta depending on the position type
| Option type | Sign of delta |
|---|---|
| Long call | + |
| Short call | – |
| Long put | – |
| Short put | + |
The delta changes with the price of underlying as well as time decay. Deep ITM options approaching expiry have deltas approaching 1, as it is almost certain that they would be exercised. Conversely, delta for deep OTM options is close to 0. ATM options have delta around 0.5, as there is a 50 per cent chance of exercise.
Gamma
Gamma is the rate of delta change, i.e. by how much the delta changes for 1 unit change in the value of the underlying. To put this into real-life perspective, if option was akin to distance travelled, delta would be velocity and gamma acceleration.
Mathematically, delta is the first derivative of option value with respect to the underlying and gamma is the second derivative. Gamma is very important for hedging strategies. If a trader’s position was delta neutral, but the option had high gamma, that would imply potential rapid change in delta, making the hedge only temporarily effective. The re-hedging would have to be done so frequently that it would become impractical and prohibitively expensive. To derive a new delta value when the underlying price increases, gamma is always added whether the long position is a call or a put, as the call becomes more ITM and the put more OTM and vice versa.
In summary:
Key Point
Long calls and puts have positive gamma.
Short calls and puts have negative gamma.
As discussed previously, deltas change most rapidly for ATM options close to expiry, as there is a 50–50 chance that the option will be exercised and even the slightest movement tips the balance from ITM to OTM position. That implies the highest gamma. Equally, deep ITM and OTM options are almost certain to remain that way; hence gamma is close to zero.
Vega
Vega (kappa or zeta) is the change in option price for a 1 per cent change in the market-implied volatility. Intuitively ATM options have the highest vega, but as the volatility increases their vegas are relatively unaffected. This is because the ATM option has a 50–50 chance of being exercised, regardless by how much the underlying moves one way or the other. However, the ITM and OTM positions have lower vegas, but as volatility increases, so does the vega. This is because the higher volatility could move even the deep ITM or OTM option in the opposite direction.
Key Point
Long calls and puts have positive vega.
Short calls and puts have negative vega.
Theta
Theta is the measure of change in option price for a time decay of one day. It is taken as absolute value, thus the value of theta is added or subtracted from the option premium, depending on the option type.
Key Point
Long calls and puts have negative theta.
Short calls and puts have positive theta.
Rho
Rho is the measure of option premium sensitivity to a 1 per cent change in interest rates. As the interest rates affect option values differently, depending on the option type (as seen earlier), a short summary of rho can only be reduced to:
Key Point
Options whose value increases with interest rates have positive rho.
Options whose value decreases with interest rates have negative rho.
In summary, the different contract types will have option sensitivities to all factors (see Table 9.3).
Table 9.3 Option sensitivities depending on the contract type
OPTION PRICING: PRACTICAL IMPLEMENTATION
Binomial trees vs. Black–Scholes
When pricing options two approaches can be taken: numerical (using binomial trees) and analytical (using the Black–Scholes equation). The Black–Scholes model revolutionised derivatives trading when the two scientists Fischer Black and Myron Scholes introduced it in their 1973 paper, ‘The pricing of options and corporate liabilities’. It simplified the pricing process as the options premiums could be calculated instantly, compared to the numerical methods which could be time-consuming. It was originally intended for pricing stock options. However, its use has since been extended to encompass many other types of options, introducing many assumptions and approximations. Since both numerical and analytical methods have their pros and cons, both are included in this chapter.
Option pricing using binomial trees
Binomial trees are a numerical method used to price options. The technique is useful as it is easy to understand and to follow the pricing steps. The main characteristics of the trees are:
General principles
- Typically used to price options on an underlying variable (e.g. stock).
- Assume that the stock price movements consist of very small binary steps in very short time intervals. The time to maturity is divided into small intervals and at each interval the stock price can only go up or down by a predetermined amount. The probability of up and down movements is assigned.
- Since payoff at maturity is known, it can be calculated at each branch of the tree. We then work backwards to find the price of the option today.
Pros and cons
- Useful for pricing products where decisions can be made at each step (e.g. American options).
- Useful for pricing dividend paying stocks.
- Can price options on indices, currencies and futures contracts.
- Can vary variables (interest rates, volatility) between the tree nodes.
- Can be used in conjunction with control variate techniques. For example, we can calculate the European option price using the Black–Scholes formula and compare it with the price obtained from the binomial tree. Assuming that this is the error that tree introduces into pricing, we can then adjust the price of an American style option (obtained using the tree) by this amount.
- Can be easily extended to non-recombining trees, trees with more than up/down movements (e.g. trinomial trees have a mid-path as well).
- Time-consuming, computationally extensive.
- Not suitable for derivatives dependent on past history.
Pricing European options using binomial trees
Constructing the tree
Binomial trees are used to model the evolution of the stock price over time. The timeline until expiry is divided into a number of steps. At each step the price can either go up or down (hence the name binomial). The up and down moves have a probability assigned to them and at each move a certain price change is allowed. As we increase the number of time steps, we can reduce the size of the price movements.
For example, from today until one year later it is quite realistic that the stock price can move from 100 to 120 or 80. If we divide the year into monthly intervals, then we can say that each month the price should not rise/fall by more than 2. Reducing the steps even further to one day or one hour, we will build a quite realistic picture of the price movements, but by now we will have too many steps to cope with. For illustration purposes, we will have only two steps in our tree. The terminology is the same as in Chapter 13 on probability and statistics:
- p is the probability of an upward move
- 1 – p is the probability of downward move
- u is the amount by which the price moves up
- d is the amount by which the price moves down.
The above quantities can be calculated using the current market conditions: volatility of the stock price and the forward stock price. This is to ensure that we are pricing the option fairly, i.e. in the risk-neutral way.
The probability weighted forward price that we are calculating must be equal to the current market forward price:
Calculation Summary: Probability-weighted stock price
![]()
As fwd(S) is equal to S × ert where r is the risk-free interest rate, we have:
u × p + d × (1 − p) = ert = R
hence
p = (R − d)/(u − d)
From the market volatility we can calculate the up and down price movements as:
![]()
The above equations are sufficient for calculation of u, d and p. Knowing them, we can begin the tree construction.
Example
In this example the price of the long call position is calculated. As it is easier to use round figures (which does not happen often using market values) we will assume the following:
The stock price tree is as follows:
The probability of reaching D is the probability of moving up and then up again, i.e. 0.6 × 0.6 = 0.36. For E we can go up and down or down and up, hence 0.6 × 0.4 = 0.24 and so on.
The probability tree will look like:

Below are three different methods of calculating the option price.
Method 1
As the option can only be exercised at expiry, we are only interested in its value at the end of one year.
The intrinsic value of the option at each node will be calculated as the option payout multiplied by the probability of reaching that node. For a call option, its payout is equal to max(S – X, 0), or for the three nodes D, E and F:

Therefore today’s price of the one-year call option with strike £100 is £3.6.
Method 2
This method is used most often when option prices are calculated. It works backwards from the expiry node by node until we reach today. The payout profile and the probability tree are the same as above.
We already know the value of the option at expiry (D, E and F). Moving backwards, we will calculate values at B and C and then from those values, the final (today’s) option price at node A.
Node B
From B we can either go up to D or down to E, hence the option value at B must be equal to the probability-weighted average of the values at D and E discounted back:
B = (0.6 × 11 + 0.4 × 0)/1.05 = 6.286
Similarly for C we have:
C = (0.6 × 0 + 0.4 × 0)/1.05 = 0
Using the above, for A we have:
A = (0.6 × 6.286 + 0.4 × 0)/1.05 = 3.59
So the option price today is £3.59. The small difference between the two results is in the fact that we used a 10 per cent annual rate in the first one, and in the second 5 per cent for each six-month period, which when compounded adds up to 10.25 per cent. This was done for the simplicity of the illustration.
Method 3
This method is known as the hedge ratio method, as it calculates the ratio of the change in the option price vs. stock price. The hedge ratio has to be calculated at every step of the tree. This means that it has to be calculated for nodes B, C and A. Just for the illustration of the method we will ignore the intermediate steps and assume that we go from today to expiry in a single step. We can see that the maximum difference in share price is 40, whilst for option payout it is 11. Therefore to cancel out gains and losses we would need 11/40 shares for every option sold. This is a hedge ratio and can be written as:
Calculation Summary: Option pricing hedge ratio
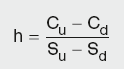
where Cu, Cd, Su and Sd are the call payout if the price goes up or down, and the stock value for the price up and down respectively.
To see if our hedge works, we buy 11 shares and sell 40 call options:

This means that we have 891 no matter how the market moves, i.e. what we own today (11 shares + 40 calls) has to be equal to the PV of £891. This method is also referred to as risk-neutral pricing, as we are neutral to the movements in the underlying. Hence, given that our stock is valued at 1100 and we have purchased 40 calls, to retain the risk-neutral position we can calculate the price of call as:
1100 − 40C = 891/1.1; C = 4.75
We can see that the price does not quite agree with the previous methods. This is partly due to the removal of the intermediate steps, but also because we did not use the probability of up and down moves. In the original examples, upward moves had a higher probability, whilst this method implicitly assumes a 50–50 chance of any move, hence the difference in valuation.
The above equations can be written mathematically as:
Calculation Summary: Pricing options using hedge ratio
where hedge ratio is calculated as:
Pricing American style options
The difference between American and European style options is that the former can be exercised at any time, whilst for the latter we have to wait until expiry. It can be shown that it is rarely optimal to exercise options early, i.e. only if the value of the option is less than the price realised on early exercise. Hence the pricing approach is the same as above, using any of the three methods, whereby at each node, the higher of the two calculated prices (market value and option intrinsic value) is used in the lattice.
Valuing other options
Valuation of other types of options (dividend paying stock options, cross-currency options etc.) is done in a similar way to that just described. The tree is built in the same way, but the probabilities and hedge ratios have to be slightly adjusted.
Dividend paying stock options
Alternatively, if we use the hedge ratio, the mathematical formula becomes:
Cross-currency options
Similarly, in the hedge ratio formula, yield will be replaced by the foreign currency interest rate rf.
Black–Scholes model
The Black–Scholes (B–S) model and its variants have become very popular, as with only one formula we can replicate the very time-consuming construction of a binomial tree. The most basic B–S formula relates to pricing European options on non-dividend-paying stocks. As such, it has little practical use in pricing interest rate derivatives. However, many interest-rate-based products can be priced using a slight modification of B–S (Black model, briefly described below), because the model does not allow early exercise, and if that is the case interest rates are assumed to behave as tradable assets.
The B–S model is expressed by the following formula:
Calculation Summary: Black–Scholes model
Where:
Calculation Summary
where:
S = underlying stock/share price
X = exercise price
r = annual continuously compounded risk-free rate
t = time (in years)
σ = annual stock price volatility
N(d) = cumulative probabilities that the deviations less than d will occur in an normal distribution with a mean of 0 and standard deviation of 1
N(d1) = probability of the stock price rising to a certain level
N(d2) = probability of the stock price rising above the strike (but it is irrelevant by how much).
These are the main assumptions that restrict the usage of the B–S model:
- The underlying asset does not pay dividends or accrue interest.
- The option is European style (no early exercise).
- The risk-free interest rate is constant over the life of the option.
- Spot movements on different dates are independent.
- The volatility of the asset price is constant over the life of the option.
- There is very low probability of large spot movements.
- The underlying asset price is log-normally distributed.
- There are no costs/taxes and trading is continuous.
- Short selling of securities (selling securities that are not owned at inception) is permitted.
The above assumptions are discussed in more detail below:
1. The underlying asset does not pay dividends or accrue interest
This is easily overcome by reducing the stock price by the present value of dividends. Alternatively, dividends can be converted into a yield on stock, and the stock price discounted using this yield.
2. The option is European style (no early exercise)
This is generally not a restriction, as it is rarely optimal to exercise early. However, early exercise on dividend-paying stock entitles the holder to dividends, thus their value may exceed the time value of the option. Early exercise may also be optimal in cross-currency options, where lower yielding currency is converted into a higher-yielding one, as higher yield may compensate for the loss of optionality.
3. The risk-free interest rate is constant over the life of the option
The assumption of constant rates has a twofold effect on the option value; it affects the option premium and some underlying assets such as currencies and bonds.
As discussed earlier, the interest rate effect on the option premium (rho) depends on the type of option:
Options on physicals (e.g. stocks)
CALL Rho + PUT Rho – Options on futures (premiums paid up-front)
CALL Rho + PUT Rho – Options on futures (premiums margined)
CALL Rho = 0 PUT Rho = 0
Options on physicals (e.g. stocks)
A seller of a call will typically hedge the position by buying stock. In the increasing interest rate environment, the cost of financing the purchase will rise, increasing the call premiums. A seller of a put would short sell some stock as a hedge strategy. Due to the increased interest rates the money received can be reinvested at higher rate, reducing the put premiums. The dividend payments until expiry are captured by reducing the stock price by the present value of dividends. This is reflected in the Black–Scholes formula:
Calculation Summary: Black–Scholes for options on physicals
Options on futures (premiums paid up-front)
Options on futures are exchange-traded products, hence the rules of the exchange specify if the option premiums are to be paid up-front or margined daily. As options on futures are cash-settled, there is no delivery or cost of carry. If the premium is paid in advance, the increase in interest rates will result in reduced PV of the option premium. Therefore for both calls and puts the option price declines with the rise in interest rates. The Black–Scholes formula is modified to:
Options on futures (premiums margined)
If the exchange rules specify that the option positions are to be margined, the interest rate fluctuations do not affect the option position. The daily margins paid/received directly reflect interest rate movements; hence both call and put premiums are unaffected. The Black–Scholes formula is modified to:
Calculation Summary: Black–Scholes for options on futures (premiums margined)
Currency options
In currency options, the foreign currency is treated similarly to dividends in stock options; any increase in its value reduces the value of calls and increases the values of puts. The effect of domestic currency is always the opposite. The Black–Scholes formula is modified to:
Calculation Summary: Black–Scholes for currency options
The interest rate effect on the value of the underlying asset is an asset valuation issue, rather than an option pricing issue. However, the value of the interest rate derivatives (e.g. swaptions) is affected by both the option and the asset valuation. Here rates are typically taken to be stochastic for the purpose of asset valuation, whilst for discounting purposes they are taken to be deterministic. Even though this is incorrect, in practice discounting is done at a financing rate for the purpose of P&L calculation. Since the cost of funds is typically fixed, the use of deterministic yields is not entirely wrong.
4. Spot movements on different dates are independent
It is likely that there is a relationship between the moves in stock prices from one day to the next. However, in the efficient markets, any trends are quickly eliminated, hence this assumption is deemed insignificant.
5. The volatility of the asset price is constant over the life of the option
This is an unrealistic simplification, as most stocks have periods of high and low activity (ultimately when markets are closed the volatility is zero). Thus constant volatility assumption results in options being under- or overvalued at some points over the option lifetime. However, if constant volatility is assumed to be equal to the weighted average of the volatilities over the lifetime of the stock, it will yield correct option valuation.
6. There is very low probability of large spot movements
The probability distribution function implicit in the B–S formula does not assign enough probability to large price movements. Hence implied volatility is not consistent across the option strikes; it increases for ITM and OTM options, creating a smile effect. This anomaly is well known in the market and various skew/smile adjustments exist to counteract this problem.
7. The underlying asset price is log-normally distributed
The log-normal distribution is very intuitive way to model asset prices, as it does not allow negative prices and it places equal probability on the price halving as for it doubling. However, log-normal distribution does not allow for bond pull-to-par (bond prices approach the redemption value as the redemption date gets nearer). Furthermore, it does not allow for mean reversion in interest rate derivatives products (interest rates will eventually converge to a long-term mean). This cannot be overcome by the B–S itself, but various modifications (such as pre-processing the input parameters to introduce the mean reversion variable) are typically done.
8. There are no costs/taxes and trading is continuous
The effect of costs and taxes can be easily overcome by modifying the stock price (as those costs will be known). This only becomes an issue in high gamma scenarios when costs of frequent re-hedging can be prohibitively large.
Continuous trading/hedging is impossible; hence the response to any large market movements can take time. Hedging is also done only periodically in order to save on transaction costs. Those assumptions cannot easily be dealt with and the best way is to have a prudent reserve in place that would account for potential closeout losses.
9. Short selling of securities is permitted
Short selling (selling ‘naked options’ without holding the underlying) is not available to all market participants. Hence this assumption does not take into account the cost of carry (transaction costs and expenses related to holding a position in the underlying). This may be accounted for through bid/offer spreads or additional reserves.
Black model
The Black model was developed for pricing interest rate derivatives. It is a slight modification of the original B–S model, thus all the assumptions and limitations of B–S still apply. Interest rates are not tradable assets. However, if the options are carried until maturity they can be valued in the same way as stock options.
By analogy with the B-S formula, the value of a call option is given by:
Calculation Summary: Black model for interest rate derivatives
where:
where F is the current market forward swap rate, and Rx is the underlying swap rate (option strike). All other variables have the same meaning as before.
The above formula is used to price vanilla caps and floors (calls and puts on the underlying interest rate), described in Chapter 12.