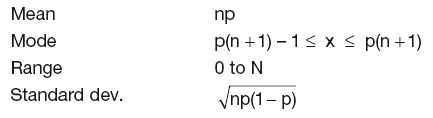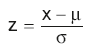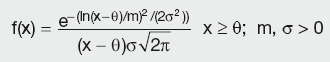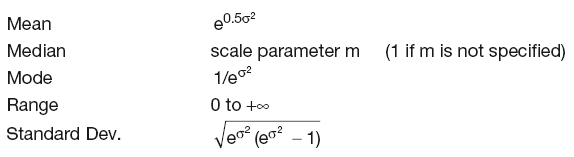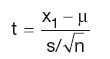Probability and statistics
The main concepts of probability
The concept of probability distribution
Types of probability distribution
Other probability distributions
INTRODUCTION
As we saw in Chapter 9, pricing derivatives, particularly securities with embedded optionality, requires assumptions on their future behaviour. Whether it is just the range of final values the security is likely to have, the paths it took to get there, or the future behaviour of several variables that impact on the value of derivative, they all require the use of probability and statistics. Hence this chapter is devoted to the main concepts of probability, together with probability distributions most relevant to financial modelling.
DEFINITION OF PROBABILITY
Very few things in life are certain. That is why we need some probability measure in order to estimate the likelihood of uncertain events. Probability theory aims to facilitate decision making where there are several possible outcomes. It was first developed for use in gambling, hence most examples use cards, coins, dice etc.
The financial world is very uncertain and decisions on investments have to be based on ‘educated guesses’. Hence probability theory plays a big part in pricing and trading financial instruments.
THE MAIN CONCEPTS OF PROBABILITY
The probability of an event E occurring in a trial where there are several equally likely outcomes is:
Calculation Summary
P(E) = Number of ways E can occur / Total number of possible outcomes
Example
When rolling a dice, what is a probability of getting six?
As there are six equally likely numbers, the probability of throwing any one of them is 1/6.
This works well with cards, coins etc., i.e. whenever all the possible outcomes are known with certainty. But what happens when this is not the case?
The probability definition has to be extended to cater for such cases. The only approach that can be taken is to observe a sufficiently large number of trials and assume that the same frequency of a different event would continue into the future. In other words, probability can be defined as:
Calculation Summary
| P(E) = | Number of observed occurrences of E / Total number of observed occurances |
Example
If 100 people took a driving test and 54 passed, we can conclude that the probability of passing the test is:
P(pass) = 54/100 = 0.54 or 54%
Normally a much larger sample would be used, but the same logic would apply.
It is worth pointing out that the above discussion applies to ‘countable’ events (events where the number of instances can be observed exactly). In order to allow for events that are not discrete, the concept of distribution functions has to be introduced (discussed later).
Probability values
From the above examples it can be seen that probability ranges from 0 (0 per cent) to 1 (100 per cent). This means that event E that will certainly not occur has probability P(E) = 0 and the event that will certainly occur will have probability P(E) = 1. It follows from these definitions that the probabilities of all possible outcomes must add up to 1, as it is certain that one of them will occur. For example, when tossing a coin, the probability of both head and tail is 0.5, hence the probability of both events is 1, as it is certain that one will occur. The above definitions can be further extended to include the concept of NOT (probability of something not happening).
Example
When rolling a dice, the probability of six is 1/6. The probability of NOT throwing six must then be the probability of all other events (1, 2, …, 5), i.e. 5/6.
However, as we know that the probability of all events is 1, then the probability of all events but six must be
P(NOT 6) = 1 − P(6) = 1 − 1/6 = 5/6
In the above example either solution was equally easy, but the concept can come in really useful if not all the possible outcomes, or the probabilities of some of the outcomes, are known.
Joint probability
The probability of occurrence of two or more events often needs to be calculated, which requires the knowledge the relationship between those events. The tests in the experiments can be:
Independent, i.e. the outcome of one test has no impact on another
Dependent, the outcome of one test is affected by the preceding tests.
Furthermore, the outcomes from any one of the tests undertaken can be:
Mutually exclusive, i.e. they cannot occur simultaneously
Not mutually exclusive, i.e. they may occur together.
Example
A card randomly selected from a pack will affect all the future draws from the same pack unless it is replaced. Two random draws from the same pack are only independent if the card is returned to the pack.
Drawing a five and a spade are two non-exclusive events, as there is a card five of spades. However, drawing five of spades twice in a row (without returning the card into the pack) are two mutually exclusive events, as there is only one such a card, and can be drawn either on the first draw, on the second or not at all, but never twice.
These statements can be expressed by mathematical formulae as below.
Independent events
Summation rule
The probability of either of the two independent events occurring is equal to the sum of their individual probabilities:
Calculation Summary: Probability of occurrence of either independent event
P(A or B) = P(A) + P(B)
Example
We are throwing two dice. What is the probability of getting number three on either of the two dice?
P(3) = 1/6
Since two throws are independent, the probability of the second draw is unaffected by the first outcome. Hence, P(3 or 3) = P(3) + P(3) = 1/3 Mathematically, the summation rule corresponds to the operation OR.
Multiplication rule
The probability of two independent events occurring simultaneously is equal to the product of their individual probabilities:
Calculation Summary: Probability of simultaneous occurrence of independent events
P(A and B) = P(A) × P(B)
Example
Using the same example as above (throwing two dice) what is the probability of getting number three on both?
P(3) = 1/6
Since two throws are independent, the probability P(3 and 3) = P(3) × P(3) = 1/36
Mathematically, the multiplication rule corresponds to the operation AND.
Dependent events
Summation rule
The probability of either one of the two dependent events occurring is equal to the sum of their individual probabilities minus their joint probability. This is because if both events can happen simultaneously, we will count their joint probability twice. Mathematically we can write this as:
Calculation Summary: Probability of occurrence of either dependent event
P(A or B) = P(A) + P(B) − P(A and B)
Example
What is the probability of drawing a five or a diamond from a pack of cards?
There are 13 diamonds and 4 fives. Hence, it could be concluded that there are 17 ways of drawing either a five or a diamond. In fact, since one of these cards is a five of diamonds, it would be counted twice. Hence:
Probability of drawing a diamond is: P(D) = 13/52
Probability of drawing a five is: P(5) = 4/52
Probability of drawing a five and a diamond is: P(5 of diamonds) = 1/52
P(5 or diamond) = P(D) + P(5) – P(5 D) = 13/52 + 4/52 – 1/52 = 16/52 = 4/13
Multiplication rule
Rules describing dependent events deal with conditional probability, as occurrence of one event influences the outcome of the other.
When two events are dependent, the probability of both occurring is:
Calculation Summary: Probability of simultaneous occurrence of dependent events
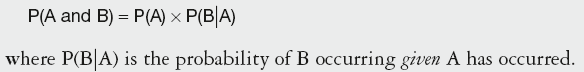
Example
Students had two maths tests. 25% of students passed both tests and 42% passed the second test. What percentage of students who passed the first test also passed the second test?
A − first test B − second test
P(A and B) = 0.25
P(B) = 0.42
P(B|A) = P(A and B)/P(B) = 0.25/0.42 = 60%
Another example of a dependent event is drawing cards at random without replacing them:
In any pack of cards the probability of drawing a spade is 13/52 = 1/4. However, the probability of drawing a spade after a spade has been drawn is:
1st draw: P(spade) = 13/52
2nd draw P(spade) = 12/51 (not 13/52 as it would be if we replaced the first card)
hence drawing two spades without replacing is:
P(2 spades) = 13/52 × 12/51 = 3/51 = 1/17
which is lower than the probability without replacing (1/16).
THE CONCEPT OF PROBABILITY DISTRIBUTION
When tossing a coin, based on its probability, the tail would be expected 50 per cent of the time. However, if 100 tosses were made, it is possible that only 46 would occur. If this experiment was repeated many times, most likely the results would range from as low as 10 to as high as 90. If the results were plotted on the graph, we would in fact be drawing a distribution, with the majority of the results concentrating around 50, but with a very wide spread.
Probability distributions are typically defined in terms of the probability density function. There are number of probability functions used in real-life applications.
For a continuous function, the probability density function (pdf) is the probability that the variable has the value x. Since for continuous distributions the probability is equivalent to the area under the curve, the probability at a single point is zero. For this reason probability is often expressed in terms of an integral between two points.
Calculation Summary: Probability that the continuous variable x has a value between a and b inclusive
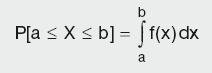
For a discrete distribution, the pdf is the probability that the variate takes the value x.
Calculation Summary: Probability that the discrete variable x has a value X or lies between a and b inclusive

The cumulative distribution function (cdf) is the probability that the variable takes a value less than or equal to x. That is:
Calculation Summary: Probability that the discrete variable x has a value less than or equal to X
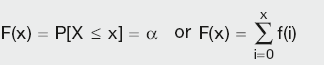
For a continuous distribution, this can be expressed mathematically as:
Calculation Summary: Probability that the continuous variable x has a value less than or equal to X
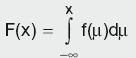
TYPES OF PROBABILITY DISTRIBUTION
There are several types of probability distributions:
- Binomial
- Normal
- Log-normal
- Poisson
- Student’s t
- χ2 (chi-square)
- Exponential
- Gamma
- Cauchy.
Each distribution is characterised by several parameters:
- Mean: the arithmetic average of all possible outcomes.
- Standard deviation: measure of dispersion of all the outcomes around the mean (width of the distribution).
- Mode: most frequent of all the outcomes.
- Median: central value of all the outcomes. If all the outcomes were arranged in ascending order according to their frequency, then median in the middle value (in the case of an odd number of outcomes) or the average of the two middle values (in the case of an even number of outcomes).
- Range: range of values that the probability distribution can take.
The above list of distributions is certainly not exhaustive. All these distributions have their application as they describe particular types of behaviour. What is common to them all is that they are trying to quantify random and uncertain events. Given that in finance events are best described using binomial, normal or log-normal distributions, the following sections will concentrate on those. Poisson, student and chi-square distributions will be described only briefly, whilst others will not be covered.
BINOMIAL DISTRIBUTION
The binomial distribution is used when there are exactly two mutually exclusive outcomes of a trial. These outcomes are appropriately labelled ‘success’ and ‘failure’. The binomial distribution is used to obtain the probability of observing x successes in N trials, with the probability of success in a single trial denoted by p. Following from the earlier observation that probabilities of all outcomes must add to 1, the probability of a failure is 1 – p. The binomial distribution assumes that p is fixed for all trials.
Example
If three cards are selected at random from a pack (each card being returned to the pack before the next one is drawn), what is the probability of drawing two spades?
Since there are four symbols in each pack (13 cards with each), the probability of any symbol (and therefore spades) is P(S) = 0.25. The probability of drawing any other symbol is P(O) = 1 – P(S) = 0.75. Since we are returning the cards to the pack, the draws are independent and the probabilities remain the same at each draw.
If we consider all possible outcomes:
SSS, SSO, SOS, OSS, SOO, OOS, OSO, OOO
We can see that their probabilities are:

However, instead of listing all possible outcomes (which can be very time-consuming), we can use the binomial expression. The formula for the binomial probability function is:
Calculation Summary: Binomial probability function
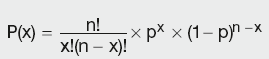
where the number of possible combinations of x successes in n trials is given by:
![]()
and the probability of x successes and n – x failures in a trial is given by:
![]()
Example
Applying this expression to the above example, we have:
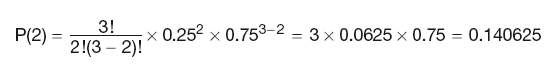
which is much simpler than listing all the outcomes!
Properties of binomial distribution
Graphical representation of binomial distribution – a histogram – is a plot of all the outcomes along the x-axes with their corresponding frequency/number of trials along the y-axes. Probability of observing a value between two points a and b is a sum of probabilities of all the points between a and b. If p = 0.5, the distribution is symmetric (the histogram is centred around p = 0.5), with p < 0.5 it is positively skewed (more items lie above the most frequent item), whilst for p > 0.5 it is negatively skewed.
Below are some statistics for the binomial distribution:
Application in financial modelling
Binomial distribution is widely used in building binomial trees (for pricing options). Here it is assumed that the price can only go up or down and each move has a probability assigned to it. The advantage of a binomial model is that it is tractable and easy to understand, but building trees can be very time-consuming and inefficient. An example of building a binomial tree to price options was given in Chapter 9 and is further shown below.
NORMAL DISTRIBUTION
Binomial distribution deals with discrete data with only two possible outcomes. Normal distribution enables us to calculate probabilities of outcomes when the variable is continuous (data can take any value). There are many similarities between normal and the symmetrical binomial distribution, so that binomial distribution can be approximated by the normal distribution when there is a large data sample. However, whilst binomial distribution dealt with discrete values and its graphical representation was given by a histogram, normal distribution is represented by a continuous curve. The probability of observing a value between any two points is equal to the area under the curve between those points.
The main characteristics of normal distribution are:
- It is bell-shaped
- It is symmetrical
- The mean, median (central point) and mode (most frequent value) are equal
- It is asymptotic (tails never reach the x-axis)
- Total area under the curve = 1
- Area under the curve between any two points gives the probability of observing a value in that range
- Standard deviation measures the spread (width) of the distribution.
The general formula for the probability density function of the normal distribution is:
Calculation Summary: Normal distribution function
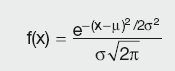
where – is the location parameter (centre of the distribution) and – is the scale parameter (determines total area under the curve). The case where – – 0 and – – 1 is called the standard normal distribution.
The equation for the standard normal distribution is:
Calculation Summary: Standard normal distribution function
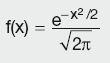
Some of the distribution statistics are:
| Mean | location parameter μ |
| Median | location parameter μ |
| Mode | location parameter μ |
| Standard dev. | scale parameter σ |
The location and scale parameters of the normal distribution can be estimated with the sample mean and sample standard deviation respectively.
The normal distribution is widely used. This is partly due to the fact that it is well behaved and mathematically tractable. However, the central limit theorem provides a theoretical basis for why it has wide applicability; it states that as the sample size (N) becomes large, the following occur:
- The sampling distribution of the mean becomes approximately normal regardless of the distribution of the original variable.
- The sampling distribution of the mean is centred at the population mean –, of the original variable.
- The standard deviation of the sampling distribution of the mean approaches σ/√N.
It may be interesting to note that the probability of observing a value in various intervals is as follows:
| Interval | Probability |
|---|---|
| μ ± 0.67σ | 0.5 |
| μ ± σ | 0.683 |
| μ ± 2σ | 0.955 |
| μ ± 2.33σ | 0.99 |
| μ ± 3σ | 0.997 |
Rather than using the distribution formula above, when the population is normally distributed the probability of observing a value in a particular range can be calculated using the z value:
i.e. the distance of the observed value x from the mean μ expressed in standard deviation σ. This way all the values are standardised and probability can be looked up in normal distribution tables.
Normal distribution tables
There are several types of distribution tables, but the most common ones give the probability of observing a value beyond a point when moving away from the mean (in either a positive or a negative direction).
Example
If a stock price is 200 and the standard deviation is 40, what is the probability of:
- A stock price falling below 150?
- A stock price within one standard deviation?
- A stock price rising to at least 220?
To answer these questions, the Z value for each case has to be calculated and the probability value found in the distribution table.
- For x = 150 we have Z = (150–200)/40 = –1.25
The negative value corresponds to the point below the mean. In the distribution tables, the absolute value is found and interpreted according to the sign of the Z value.
In our case the probability corresponds to Z = 1.25 = 0.10565. This is the area of the curve beyond the point away from the mean. Hence for Z = –1.25 it corresponds to the stock values below 150. - Here P(160 ≤ x ≤ 200) + P(200 ≤ x ≤ 240) is required, which is the same as taking the area P(x ≤ 200) – P(x ≤ 160) twice, as the curve is symmetrical.
Since P(≤ 200) = 0.5 and the probability P(≤ 160) can be calculated as Z = (160-200)/40 = −1, with a corresponding probability of 0.15866, the probability of the stock price falling within one standard deviation of the mean is P = 2×(0.5 – 0.15866) = 0.6827 - Finally, the probability of the stock price rising to at least 220 is calculated as Z = (220–200)/40 = 0.5, which corresponds to P(≥ 220) = 0.30854
Application in financial modelling
The most famous application of normal distribution is in the Black–Scholes formula. It is used for pricing stocks, interest rate derivatives etc. In principle, products that have some built-in optionality will have to assume a type of distribution that the underlying variable takes. Then the stochastic behaviour of the variable can be modelled and the product priced depending on the probabilities of all possible states. Good examples are:
- Caps, floors, collars
- Range accruals
- Limited price index (LPI) swaps etc.
Whether normal or log-normal (or shifted log-normal) distribution is used is mostly a matter of the practitioner’s choice and the empirical evidence of variable behaviour.
LOG-NORMAL DISTRIBUTION
In the standard normal distribution the horizontal scale is linear, which means that for a mean = 100 the probability of 80 is the same as the probability of 120. In log-normal distribution the x-axis would be linear if logarithms of values were plotted. This implies that for a mean = 100, the probability of 200 is the same as the probability of 50.
More formally, a variable X is log-normally distributed if Y = ln(X) is normally distributed, with ln denoting the natural logarithm. The general formula for the probability density function of the log-normal distribution is:
Calculation Summary: Log-normal distribution function
where σ is the shape parameter (allowing for different shapes of distribution), θ is the location parameter (centre of the distribution) and m is the scale parameter (determining the area under the curve). The case where θ = 0 and m = 1 is called the standard log-normal distribution. The case where only θ = 0 is called the two-parameter log-normal distribution.
The equation for the standard log-normal distribution is:
Calculation Summary: Standard log-normal distribution function
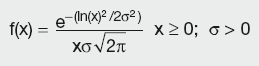
The most important distribution statistics for θ = 0 and m = 1 are:
Application in financial modelling
Many models (the interest derivative ones in particular) rely on log-normal distribution. In most cases interest rates are modelled as if they behave log-normally, hence this distribution is used directly in equations as well as in model calibration. Often in modelling shifted log-normal distribution is used (the larger the shift, the more it resembles normal distribution). There is ample empirical evidence to suggest that the stock prices also behave log-normally.
OTHER PROBABILITY DISTRIBUTIONS
Poisson distribution
The Poisson distribution is a discrete distribution that takes on the values x = 0, 1, 2, 3 etc. It is often used as a model for the number of events (such as the number of telephone calls at a business centre or the number of accidents at an intersection) in a specific time period. It is also useful in ecological studies, particle physics etc. The useful characteristic of the distribution is that it is not invalidated if one event replaces another, e.g. when counting photons hitting an x-ray target in a given time interval any missed photon can be replaced by a new incoming one.
The Poisson distribution is determined by one parameter, lambda. Lambda is a shape parameter specifying the average number of events in a given time interval. The probability density function for the Poisson distribution is given by the formula:
Calculation Summary: Poisson distribution function
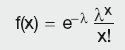
Some of the Poisson distribution statistics are:
mean = λ
Range = 0 to +∞
Standard deviation =
Student’s t-distribution
The t-distributions were discovered by statistician William Gosset who – being employed by the Guinness brewing company – could not publish under his own name, so he wrote under the pen name ‘Student’.
T-distributions are normally used for hypothesis testing and parameter estimation, and very rarely for modelling. They arise in simple random samples of size n, drawn from a normal population with mean μ and standard deviation σ. Let x1 denote the sample mean and s, the sample standard deviation. Then the quantity
has a t-distribution with n–1 degrees of freedom.
Note that there is a different t-distribution for each sample size, in other words, it is a class of distributions. For any specific t-distribution, the degrees of freedom have to be specified. They come from the sample standard deviation s in the denominator of the equation.
The t-density curves are symmetric and bell-shaped like the normal distribution and have their peak at 0. However, the spread is wider than in the standard normal distribution. This is due to the fact that, in the above formula, the denominator is s rather than σ. Since s is a random quantity varying with various samples, there is greater variability in t, resulting in a larger spread.
The larger the number of degrees of freedom, the closer the t-density is to the normal density. This reflects the fact that the standard deviation s approaches σ for large sample size n.
Chi-square (χ2) distribution
The chi-square distribution results when ν independent variables with standard normal distributions are squared and summed. For simplicity the formula for probability density function is not included in this text. The chi-square distribution is typically used to develop hypothesis tests and confidence intervals and rarely for modelling applications.
Some of the χ2 distribution statistics are:
mean = ν
Range = 0 to +∞
Standard deviation =
BINOMIAL TREES
Binomial trees are used to model the behaviour of a variable that can take only discrete values, e.g. to estimate the probability of the fuel price reaching a certain level in the future. The price can ultimately either go up or down, i.e. change in only two possible ways, hence the name binominal. We can crudely break down the timeline to only now and the future date and take a guess at the possible up and down price movements. But a more practical approach would be to divide the timeline until the future date into a number of steps. The probability of up and down moves is assigned and at each move a certain price change is allowed. Those values can be constant for the entire tree, or change at every step. The size of the price movements reduces by increasing the number of time steps.
Example
If the current price is 100, two months later it might be as high as 120, or as low as 90. If we divide this period into monthly intervals, we will have only two steps in our tree.
We assign:
p is the probability of an upward move
1 – p is the probability of a downward move
u is the amount by which the price moves up
d is the amount by which the price moves down.
The above variables can be estimated from the market conditions, but for illustration purposes we will assume that:
p = 0.7
1 –p = 0.3
u = 10
d = 5
Hence the probability tree will look like:

The probability of reaching D is the probability of moving up and then up again, i.e. 0.7 × 0.7 = 0.49. For E we can go up and down or down and up, hence 0.7 × 0.3 = 0.21 and so on.
The tree showing possible prices is as follows:
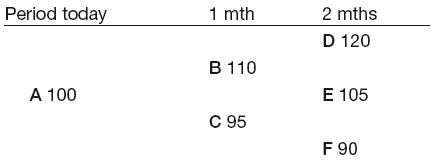
As we are only interested in the price at the end of one year, we can see that it can take (in our estimate) three possible values ranging from 90 to 120, but the least likely outcome (only 9% probability) is 90, whilst it is over 90% certain that it would increase from the original value.
The above was a very trivial example, but this principle can be extended to any real-life problem to assess the probability of different outcomes.