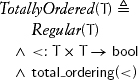Chapter 4

Linear Orderings

This chapter describes properties of binary relations, such as transitivity and symmetry. In particular, we introduce total and weak linear orderings. We introduce the concept of stability of functions based on linear ordering: preserving order present in the arguments for equivalent elements. We generalize min and max to order-selection functions, such as the median of three elements, and introduce a technique for managing their implementation complexity through reduction to constrained subproblems.

4.1 Classification of Relations

A relation is a predicate taking two parameters of the same type:

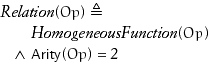
A relation is transitive if, whenever it holds between a and b, and between b and c, it holds between a and c:

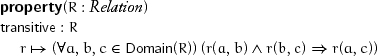
Examples of transitive relations are equality, equality of the first member of a pair, reachability in an orbit, and divisibility.

A relation is strict if it never holds between an element and itself; a relation is reflexive if it always holds between an element and itself:

All the previous examples of transitive relations are reflexive; proper factor is strict.

Exercise 4.1 Give an example of a relation that is neither strict nor reflexive.

A relation is symmetric if, whenever it holds in one direction, it holds in the other; a relation is asymmetric if it never holds in both directions:

An example of a symmetric transitive relation is “sibling”; an example of an asymmetric transitive relation is “ancestor.”

Exercise 4.2 Give an example of a symmetric relation that is not transitive.

Exercise 4.3 Give an example of a symmetric relation that is not reflexive.

Given a relation r(a, b), there are derived relations with the same domain:

Given a symmetric relation, the only interesting derivable relation is the complement, because the converse is equivalent to the original relation.

A relation is an equivalence if it is transitive, reflexive, and symmetric:

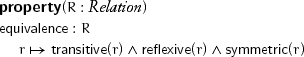
Examples of equivalence relations are equality, geometric congruence, and integer congruence modulo n.

Lemma 4.1 If r is an equivalence relation, a = b r(a, b).

An equivalence relation partitions its domain into a set of equivalence classes: subsets containing all elements equivalent to a given element. We can often implement an equivalence relation by defining a key function, a function that returns a unique value for all the elements in each equivalence class. Applying equality to the results of the key function determines equivalence:

Lemma 4.2 key_function (f, r) equivalence (r)

4.2 Total and Weak Orderings

A relation is a total ordering if it is transitive and obeys the trichotomy law, whereby for every pair of elements, exactly one of the following holds: the relation, its converse, or equality:

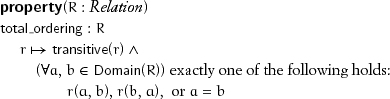
A relation is a weak ordering if it is transitive and there is an equivalence relation on the same domain such that the original relation obeys the weak-trichotomy law, whereby for every pair of elements, exactly one of the following holds: the relation, its converse, or the equivalence:

Given a relation r, the relation ¬r(a, b) ¬r(b, a) is called the symmetric complement of r.

Lemma 4.3 The symmetric complement of a weak ordering is an equivalence relation.

Examples of a weak ordering are pairs ordered by their first members and employees ordered by salary.

Lemma 4.4 A total ordering is a weak ordering.

Lemma 4.5 A weak ordering is asymmetric.

Lemma 4.6 A weak ordering is strict.

A key function f on a set T, together with a total ordering r on the codomain of f, define a weak ordering (x, y) r(f(x), f(y)).

We refer to total and weak orderings as linear orderings because of their respective trichotomy laws.

4.3 Order Selection

Given a weak ordering r and two objects a and b from r’s domain, it makes sense to ask which is the minimum. It is obvious how to define the minimum when r or its converse holds between a and b but is not so when they are equivalent. A similar problem arises if we ask which is the maximum.

A property for dealing with this problem is known as stability. Informally, an algorithm is stable if it respects the original order of equivalent objects. So if we think of minimum and maximum as selecting, respectively, the smallest and second smallest from a list of two arguments, stability requires that when called with equivalent elements, minimum should return the first and maximum the second.^[1]

We can generalize minimum and maximum to (j, k)-order selection, where k > 0 indicates the number of arguments, and 0 ≤ j < k indicates that the jth smallest is to be selected. To formalize our notion of stability, assume that each of the k arguments is associated with a unique natural number called its stability index. Given the original weak ordering r, we define the strengthened relation on (object, stability index) pairs:

((a, i_a), (b, i_b))  r(a, b)  (¬r(b, a)  i_a < i_b)

If we implement an order-selection algorithm in terms of , there are no ambiguous cases caused by equivalent arguments. The natural default for the stability index of an argument is its ordinal position in the argument list.

While the strengthened relation gives us a powerful tool for reasoning about stability, it is straightforward to define simple order-selection procedures without making the stability indices explicit. This implementation of minimum returns a when a and b are equivalent, satisfying our definition of stability:^[2]

Similarly, this implementation of maximum returns b when a and b are equivalent, again satisfying our definition of stability:^[3]

For the remainder of this chapter, the precondition weak_ordering (r) is implied.

While it is useful to have other order-selection procedures for k arguments, the difficulty of writing such an order-selection procedure grows quickly with k, and there are many different procedures we might have a need for. A technique we call reduction to constrained subproblems addresses both issues. We develop a family of procedures that assume a certain amount of information about the relative ordering of their arguments.

Naming these procedures systematically is essential. Each name begins with select_j_k, where 0 ≤j < k, to indicate selection of the jth elements from k arguments according to the given ordering. We append a sequence of letters to indicate a precondition on the ordering of parameters, expressed as increasing chains. For example, a suffix of _ab means that the first two parameters are in order, and _abd means that the first, second, and fourth parameters are in order. More than one such suffix appears when there are preconditions on different chains of parameters.

For example, it is straightforward to implement minimum and maximum for three elements:

It is easy to find the median of three elements if we know that the first two elements are in increasing order:

Establishing the precondition for select_1_3_ab requires only one comparison. Because the parameters are passed by constant reference, no data movement takes place:

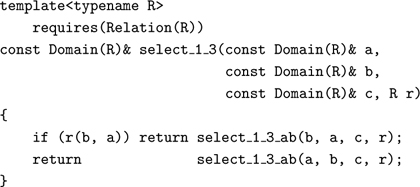
In the worst case, select_1_3 does three comparisons. The function does two comparisons only when c is the maximum of a, b, c, and since it happens in one-third of the cases, the average number of comparisons is , assuming a uniform distribution of inputs.

Finding the second smallest of n elements requires at least n + [log₂ n] – 2 comparisons.^[4] In particular, finding the second of four requires four comparisons.

It is easy to select the second of four if we know that the first pair of arguments and the second pair of arguments are each in increasing order:

The precondition for select_1_4_ab_cd can be established with one comparison if we already know that the first pair of arguments are in increasing order:

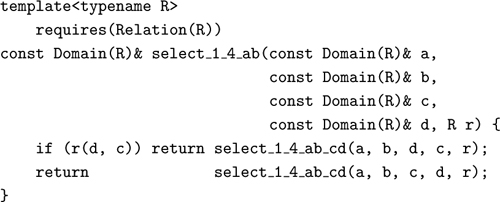
The precondition for select_1_4_ab can be established with one comparison:

Exercise 4.4 Implement select_2_4.

Maintaining stability of order-selection networks up through order 4 has not been too difficult. But with order 5, situations arise in which the procedure corresponding to a constrained subproblem is called with arguments out of order from the original caller, which violates stability. A systematic way to deal with such situations is to pass the stability indices along with the actual parameters and to use the strengthened relation . We avoid extra runtime cost by using integer template parameters.

We name the stability indices ia, ib, ..., corresponding to the parameters a, b, and so on. The strengthened relation is obtained by using the function object template compare_strict_or_reflexive, which takes a bool template parameter that, if true, means that the stability indices of its arguments are in increasing order:

template<bool strict, typename R>
    requires(Relation(R))
struct compare_strict_or_reflexive;

When we construct an instance of compare_strict_or_reflexive, we supply the appropriate Boolean template argument:

We specialize compare_strict_or_reflexive for the two cases: (1) stability indices in increasing order, in which case we use the original strict relation r; and (2) decreasing order, in which case we use the corresponding reflexive version of r:

When an order-selection procedure with stability indices calls another such procedure, the stability indices corresponding to the parameters, in the same order as they appear in the call, are passed:

Now we are ready to implement order 5 selections:

Lemma 4.7 select_2_5 performs six comparisons.

Exercise 4.5 Find an algorithm for median of 5 that does slightly fewer comparisons on average.

We can wrap an order-selection procedure with an outer procedure that supplies, as the stability indices, any strictly increasing series of integer constants; by convention, we use successive integers starting with 0:

Exercise 4.6 Prove the stability of every order-selection procedure in this section.

Exercise 4.7 Verify the correctness and stability of every order-selection procedure in this section by exhaustive testing.

Project 4.1 Design a set of necessary and sufficient conditions preserving stability under composition of order-selection procedures.

Project 4.2 Create a library of minimum-comparison procedures for stable sorting and merging.^[5] Minimize not only the number of comparisons but also the number of data movements.

4.4 Natural Total Ordering

There is a unique equality on a type because equality of values of the type means that those values represent the same entity. Often there is no unique natural total ordering on a type. For a concrete species, there are often many total and weak orderings, without any of them playing a special role. For an abstract species, there may be one special total ordering that respects its fundamental operations. Such an ordering is called the natural total ordering and is denoted by the symbol <, as follows:

For example, the natural total ordering on integers respects fundamental operations:

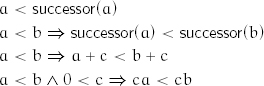
Sometimes, a type does not have a natural total ordering. For example, complex numbers and employee records do not have natural total orderings. We require regular types to provide a default total ordering (sometimes abbreviated to default ordering) to enable logarithmic searching. An example of default total ordering where no natural total ordering exists is lexicographical ordering for complex numbers. When the natural total ordering exists, it coincides with the default ordering. We use the following notation:

4.5 Clusters of Derived Procedures

Some procedures naturally come in clusters. If some procedures in a cluster are defined, the definitions of the others naturally follow. The complement of equality, inequality, is defined whenever equality is defined; the operators = and ≠ must be defined consistently. For every totally ordered type, all four operators <, >, ≤, and ≥ must be defined together in such a way that the following hold:

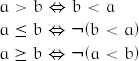
4.6 Extending Order-Selection Procedures

The order-selection procedures in this chapter do not return an object that can be mutated, because they work with constant references. It is useful and straightforward to have versions that return a mutable object, so that they could be used on the left side of an assignment or as the mutable argument to an action or accumulation procedure. An overloaded mutable version of an order-selection procedure is implemented by removing from the nonmutable version the const from each parameter type and the result type. For example, our version of select_0_2 is supplemented with

template<typename R>
    requires(Relation(R))
Domain(R)& select_0_2(Domain(R)& a, Domain(R)& b, R r)
{
    if (r(b, a)) return b;
    return a;
}

In addition, a library should provide versions for totally ordered types (with <), since it is a common case. This means that there are four versions of each procedure.

The trichotomy and weak-trichotomy laws satisfied by total and weak ordering suggest that instead of a two-valued relation, we could use a three-valued comparison procedure, since, in some situations, this would avoid an additional procedure call.

Exercise 4.8 Rewrite the algorithms in this chapter using three-valued comparison.

4.7 Conclusions

The axioms of total and weak ordering provide the interface to connect specific orderings with general-purpose algorithms. Systematic solutions to small problems lead to easy decomposition of large problems. There are clusters of procedures with interrelated semantics.