Chapter 1
Foundations
Starting with a brief taxonomy of ideas, we introduce notions of value, object, type, procedure, and concept that represent different categories of ideas in the computer. A central notion of the book, regularity, is introduced and elaborated. When applied to procedures, regularity means that procedures return equal results for equal arguments. When applied to types, regularity means that types possess the equality operator and equality-preserving copy construction and assignment. Regularity enables us to apply equational reasoning (substituting equals for equals) to transform and optimize programs.
1.1 Categories of Ideas: Entity, Species, Genus
In order to explain what objects, types, and other foundational computer notions are, it is useful to give an overview of some categories of ideas that correspond to these notions.
An abstract entity is an individual thing that is eternal and unchangeable, while a concrete entity is an individual thing that comes into and out of existence in space and time. An attribute—a correspondence between a concrete entity and an abstract entity—describes some property, measurement, or quality of the concrete entity. Identity, a primitive notion of our perception of reality, determines the sameness of a thing changing over time. Attributes of a concrete entity can change without affecting its identity. A snapshot of a concrete entity is a complete collection of its attributes at a particular point in time. Concrete entities are not only physical entities but also legal, financial, or political entities. Blue and 13 are examples of abstract entities. Socrates and the United States of America are examples of concrete entities. The color of Socrates’ eyes and the number of U.S. states are examples of attributes.
An abstract species describes common properties of essentially equivalent abstract entities. Examples of abstract species are natural number and color. A concrete species describes the set of attributes of essentially equivalent concrete entities. Examples of concrete species are man and U.S. state.
A function is a rule that associates one or more abstract entities, called arguments, from corresponding species with an abstract entity, called the result, from another species. Examples of functions are the successor function, which associates each natural number with the one that immediately follows it, and the function that associates with two colors the result of blending them.
An abstract genus describes different abstract species that are similar in some respect. Examples of abstract genera are number and binary operator. A concrete genus describes different concrete species similar in some respect. Examples of concrete genera are mammal and biped.
An entity belongs to a single species, which provides the rules for its construction or existence. An entity can belong to several genera, each of which describes certain properties.
We show later in the chapter that objects and values represent entities, types represent species, and concepts represent genera.
1.2 Values
Unless we know the interpretation, the only things we see in a computer are 0s and 1s. A datum is a finite sequence of 0s and 1s.
A value type is a correspondence between a species (abstract or concrete) and a set of datums. A datum corresponding to a particular entity is called a representation of the entity; the entity is called the interpretation of the datum. We refer to a datum together with its interpretation as a value. Examples of values are integers represented in 32-bit two’s complement big-endian format and rational numbers represented as a concatenation of two 32-bit sequences, interpreted as integer numerator and denominator, represented as two’s complement big-endian values.
A datum is well formed with respect to a value type if and only if that datum represents an abstract entity. For example, every sequence of 32 bits is well formed when interpreted as a two’s-complement integer; an IEEE 754 floating-point NaN (Not a Number) is not well formed when interpreted as a real number.
A value type is properly partial if its values represent a proper subset of the abstract entities in the corresponding species; otherwise it is total. For example, the type int is properly partial, while the type bool is total.
A value type is uniquely represented if and only if at most one value corresponds to each abstract entity. For example, a type representing a truth value as a byte that interprets zero as false and nonzero as true is not uniquely represented. A type representing an integer as a sign bit and an unsigned magnitude does not provide a unique representation of zero. A type representing an integer in two’s complement is uniquely represented.
A value type is ambiguous if and only if a value of the type has more than one interpretation. The negation of ambiguous is unambiguous. For example, a type representing a calendar year over a period longer than a single century as two decimal digits is ambiguous.
Two values of a value type are equal if and only if they represent the same abstract entity. They are representationally equal if and only if their datums are identical sequences of 0s and 1s.
Lemma 1.1 If a value type is uniquely represented, equality implies representational equality.
Lemma 1.2 If a value type is not ambiguous, representational equality implies equality.
If a value type is uniquely represented, we implement equality by testing that both sequences of 0s and 1s are the same. Otherwise we must implement equality in such a way that preserves its consistency with the interpretations of its arguments. Nonunique representations are chosen when testing equality is done less frequently than operations generating new values and when it is possible to make generating new values faster at the cost of making equality slower. For example, two rational numbers represented as pairs of integers are equal if they reduce to the same lowest terms. Two finite sets represented as unsorted sequences are equal if, after sorting and eliminating duplicates, their corresponding elements are equal.
Sometimes, implementing true behavioral equality is too expensive or even impossible, as in the case for a type of encodings of computable functions. In these cases we must settle for the weaker representational equality: that two values are the same sequence of 0s and 1s.
Computers implement functions on abstract entities as functions on values. While values reside in memory, a properly implemented function on values does not depend on particular memory addresses: It implements a mapping from values to values.
A function defined on a value type is regular if and only if it respects equality: Substituting an equal value for an argument gives an equal result. Most numeric functions are regular. An example of a numeric function that is not regular is the function that returns the numerator of a rational number represented as a pair of integers, since ![]() , but numerator(
, but numerator(![]() ) ≠ numerator(
) ≠ numerator(![]() ). Regular functions allow equational reasoning: substituting equals for equals.
). Regular functions allow equational reasoning: substituting equals for equals.
A nonregular function depends on the representation, not just the interpretation, of its argument. When designing the representation for a value type, two tasks go hand in hand: implementing equality and deciding which functions will be regular.
1.3 Objects
A memory is a set of words, each with an address and a content. The addresses are values of a fixed size, called the address length. The contents are values of another fixed size, called the word length. The content of an address is obtained by a load operation. The association of a content with an address is changed by a store operation. Examples of memories are bytes in main memory and blocks on a disk drive.
An object is a representation of a concrete entity as a value in memory. An object has a state that is a value of some value type. The state of an object is changeable. Given an object corresponding to a concrete entity, its state corresponds to a snapshot of that entity. An object owns a set of resources, such as memory words or records in a file, to hold its state.
While the value of an object is a contiguous sequence of 0s and 1s, the resources in which these 0s and 1s are stored are not necessarily contiguous. It is the interpretation that gives unity to an object. For example, two doubles may be interpreted as a single complex number even if they are not adjacent. The resources of an object might even be in different memories. This book, however, deals only with objects residing in a single memory with one address space. Every object has a unique starting address, from which all its resources can be reached.
An object type is a pattern for storing and modifying values in memory. Corresponding to every object type is a value type describing states of objects of that type. Every object belongs to an object type. An example of an object type is integers represented in 32-bit two’s complement little-endian format aligned to a 4-byte address boundary.
Values and objects play complementary roles. Values are unchanging and are independent of any particular implementation in the computer. Objects are changeable and have computer-specific implementations. The state of an object at any point in time can be described by a value; this value could in principle be written down on paper (making a snapshot) or serialized and sent over a communication link. Describing the states of objects in terms of values allows us to abstract from the particular implementations of the objects when discussing equality. Functional programming deals with values; imperative programming deals with objects.
We use values to represent entities. Since values are unchanging, they can represent abstract entities. Sequences of values can also represent sequences of snapshots of concrete entities. Objects hold values representing entities. Since objects are changeable, they can represent concrete entities by taking on a new value to represent a change in the entity. Objects can also represent abstract entities: staying constant or taking on different approximations to the abstract.
We use objects in the computer for the following three reasons.
1. Objects model changeable concrete entities, such as employee records in a payroll application.
2. Objects provide a powerful way to implement functions on values, such as a procedure implementing the square root of a floating-point number using an iterative algorithm.
3. Computers with memory constitute the only available realization of a universal computational device.
Some properties of value types carry through to object types. An object is well formed if and only if its state is well formed. An object type is properly partial if and only if its value type is properly partial; otherwise it is total. An object type is uniquely represented if and only if its value type is uniquely represented.
Since concrete entities have identities, objects representing them need a corresponding notion of identity. An identity token is a unique value expressing the identity of an object and is computed from the value of the object and the address of its resources. Examples of identity tokens are the address of the object, an index into an array where the object is stored, and an employee number in a personnel record. Testing equality of identity tokens corresponds to testing identity. During the lifetime of an application, a particular object could use different identity tokens as it moves either within a data structure or from one data structure to another.
Two objects of the same type are equal if and only if their states are equal. If two objects are equal, we say that one is a copy of the other. Making a change to an object does not affect any copy of it.
This book uses a programming language that has no way to describe values and value types as separate from objects and object types. So from this point on, when we refer to types without qualification, we mean object types.
1.4 Procedures
A procedure is a sequence of instructions that modifies the state of some objects; it may also construct or destroy objects.
The objects with which a procedure interacts can be divided into four kinds, corresponding to the intentions of the programmer.
1. Input/output consists of objects passed to/from a procedure directly or indirectly through its arguments or returned result.
2. Local state consists of objects created, destroyed, and usually modified during a single invocation of the procedure.
3. Global state consists of objects accessible to this and other procedures across multiple invocations.
4. Own state consists of objects accessible only to this procedure (and its affiliated procedures) but shared across multiple invocations.
An object is passed directly if it is passed as an argument or returned as the result and is passed indirectly if it is passed via a pointer or pointerlike object. An object is an input to a procedure if it is read, but not modified, by the procedure. An object is an output from a procedure if it is written, created, or destroyed by the procedure, but its initial state is not read by the procedure. An object is an input/output of a procedure if it is modified as well as read by the procedure.
A computational basis for a type is a finite set of procedures that enable the construction of any other procedure on the type. A basis is efficient if and only if any procedure implemented using it is as efficient as an equivalent procedure written in terms of an alternative basis. For example, a basis for unsigned k-bit integers providing only zero, equality, and the successor function is not efficient, since the complexity of addition in terms of successor is exponential in k.
A basis is expressive if and only if it allows compact and convenient definitions of procedures on the type. In particular, all the common mathematical operations need to be provided when they are appropriate. For example, subtraction could be implemented using negation and addition but should be included in an expressive basis. Similarly, negation could be implemented using subtraction and zero but should be included in an expressive basis.
1.5 Regular Types
There is a set of procedures whose inclusion in the computational basis of a type lets us place objects in data structures and use algorithms to copy objects from one data structure to another. We call types having such a basis regular, since their use guarantees regularity of behavior and, therefore, interoperability.[1] We derive the semantics of regular types from built-in types, such as bool, int, and, when restricted to well-formed values, double. A type is regular if and only if its basis includes equality, assignment, destructor, default constructor, copy constructor, total ordering,[2] and underlying type.[3]
Equality is a procedure that takes two objects of the same type and returns true if and only if the object states are equal. Inequality is always defined and returns the negation of equality. We use the following notation:
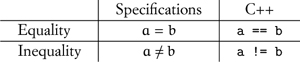
Assignment is a procedure that takes two objects of the same type and makes the first object equal to the second without modifying the second. The meaning of assignment does not depend on the initial value of the first object. We use the following notation:
![]()
A destructor is a procedure causing the cessation of an object’s existence. After a destructor has been called on an object, no procedure can be applied to it, and its former memory locations and resources may be reused for other purposes. The destructor is normally invoked implicitly. Global objects are destroyed when the application terminates, local objects are destroyed when the block in which they are declared is exited, and elements of a data structure are destroyed when the data structure is destroyed.
A constructor is a procedure transforming memory locations into an object. The possible behaviors range from doing nothing to establishing a complex object state.
An object is in a partially formed state if it can be assigned to or destroyed. For an object that is partially formed but not well formed, the effect of any procedure other than assignment (only on the left side) and destruction is not defined.
Lemma 1.3 A well-formed object is partially formed.
A default constructor takes no arguments and leaves the object in a partially formed state. We use the following notation:

A copy constructor takes an additional argument of the same type and constructs a new object equal to it. We use the following notation:
![]()
1.6 Regular Procedures
A procedure is regular if and only if replacing its inputs with equal objects results in equal output objects. As with value types, when defining an object type we must make consistent choices in how to implement equality and which procedures on the type will be regular.
Exercise 1.1 Extend the notion of regularity to input/output objects of a procedure, that is, to objects that are modified as well as read.
While regularity is the default, there are reasons for nonregular behavior of procedures.
1. A procedure returns the address of an object; for example, the built-in function addressof.
2. A procedure returns a value determined by the state of the real world, such as the value of a clock or other device.
3. A procedure returns a value depending on own state; for example, a pseudorandom number generator.
4. A procedure returns a representation-dependent attribute of an object, such as the amount of reserved memory for a data structure.
A functional procedure is a regular procedure defined on regular types, with one or more direct inputs and a single output that is returned as the result of the procedure. The regularity of functional procedures allows two techniques for passing inputs. When the size of the parameter is small or if the procedure needs a copy it can mutate, we pass it by value, making a local copy. Otherwise we pass it by constant reference. A functional procedure can be implemented as a C++ function, function pointer, or function object.[4]
This is a functional procedure:
int plus_0(int a, int b)
{
return a + b;
}
This is a semantically equivalent functional procedure:
int plus_1(const int& a, const int& b)
{
return a + b;
}
This is semantically equivalent but is not a functional procedure, because its inputs and outputs are passed indirectly:
void plus_2(int* a, int* b, int* c)
{
*c = *a + *b;
}
In plus_2, a and b are input objects, while c is an output object. The notion of a functional procedure is a syntactic rather than semantic property: In our terminology, plus_2 is regular but not functional.
The definition space for a functional procedure is that subset of values for its inputs to which it is intended to be applied. A functional procedure always terminates on input in its definition space; while it may terminate for input outside its definition space, it may not return a meaningful value.
A homogeneous functional procedure is one whose input objects are all the same type. The domain of a homogeneous functional procedure is the type of its inputs. Rather than defining the domain of a nonhomogeneous functional procedure as the direct product of its input types, we refer individually to the input types of a procedure.
The codomain for a functional procedure is the type of its output. The result space for a functional procedure is the set of all values from its codomain returned by the procedure for inputs from its definition space.
Consider the functional procedure
int square(int n) { return n * n; }
While its domain and codomain are int, its definition space is the set of integers whose square is representable in the type, and its result space is the set of square integers representable in the type.
Exercise 1.2 Assuming that int is a 32-bit two’s complement type, determine the exact definition and result space.
1.7 Concepts
A procedure using a type depends on syntactic, semantic, and complexity properties of the computational basis of the type. Syntactically it depends on the presence of certain literals and procedures with particular names and signatures. Its semantics depend on properties of these procedures. Its complexity depends on the time and space complexity of these procedures. A program remains correct if a type is replaced by a different type with the same properties. The utility of a software component, such as a library procedure or data structure, is increased by designing it not in terms of concrete types but in terms of requirements on types expressed as syntactic and semantic properties. We call a collection of requirements a concept. Types represent species; concepts represent genera.
In order to describe concepts, we need several mechanisms dealing with types: type attributes, type functions, and type constructors. A type attribute is a mapping from a type to a value describing some characteristic of the type. Examples of type attributes are the built-in type attribute sizeof(T) in C++, the alignment of an object of a type, and the number of members in a struct. If F is a functional procedure type, Arity(F) returns its number of inputs. A type function is a mapping from a type to an affiliated type. An example of a type function is: given “pointer to T,” the type T. In some cases it is useful to define an indexed type function with an additional constant integer parameter; for example, a type function returning the type of the ith member of a structure type (counting from 0). If F is a functional procedure type, the type function Codomain(F) returns the type of the result. If F is a functional procedure type and i < Arity(F), the indexed type function InputType(F, i) returns the type of the ith parameter (counting from 0).[5] A type constructor is a mechanism for creating a new type from one or more existing types. For example, pointer(T) is the built-in type constructor that takes a type T and returns the type “pointer to T”; struct is a built-in n-ary type constructor; a structure template is a user-defined n-ary type constructor.
If ![]() is an n-ary type constructor, we usually denote its application to types T0, ..., Tn−1 as
is an n-ary type constructor, we usually denote its application to types T0, ..., Tn−1 as ![]() T0, ..., Tn−1. An important example is pair, which, when applied to regular types T0 and T1, returns a struct type pairT0, T1 with a member m0 of type T0 and a member m1 of type T1. To ensure that the type pairT0, T1 is itself regular, equality, assignment, destructor, and constructors are defined through memberwise extensions of the corresponding operations on the types T0 and T1. The same technique is used for any tuple type, such as triple. In Chapter 12 we show the implementation of pairT0, T1 and describe how regularity is preserved by more complicated type constructors.
T0, ..., Tn−1. An important example is pair, which, when applied to regular types T0 and T1, returns a struct type pairT0, T1 with a member m0 of type T0 and a member m1 of type T1. To ensure that the type pairT0, T1 is itself regular, equality, assignment, destructor, and constructors are defined through memberwise extensions of the corresponding operations on the types T0 and T1. The same technique is used for any tuple type, such as triple. In Chapter 12 we show the implementation of pairT0, T1 and describe how regularity is preserved by more complicated type constructors.
Somewhat more formally, a concept is a description of requirements on one or more types stated in terms of the existence and properties of procedures, type attributes, and type functions defined on the types. We say that a concept is modeled by specific types, or that the types model the concept, if the requirements are satisfied for these types. To assert that a concept ![]() is modeled by types T0, ..., Tn−1, we write
is modeled by types T0, ..., Tn−1, we write ![]() (T0, ..., Tn−1). Concept
(T0, ..., Tn−1). Concept ![]() refines concept
refines concept ![]() if whenever
if whenever ![]() is satisfied for a set of types,
is satisfied for a set of types, ![]() is also satisfied for those types. We say that
is also satisfied for those types. We say that ![]() weakens
weakens ![]() if
if ![]() refines
refines ![]() .
.
A type concept is a concept defined on one type. For example, C++ defines the type concept integral type, which is refined by unsigned integral type and by signed integral type, while STL defines the type concept sequence. We use the primitive type concepts Regular and FunctionalProcedure, corresponding to the informal definitions we gave earlier.
We define concepts formally by using standard mathematical notation. To define a concept ![]() , we write
, we write
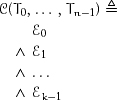
where ![]() is read as “is equal to by definition,” the Ti are formal type parameters, and the εj are concept clauses, which take one of three forms:
is read as “is equal to by definition,” the Ti are formal type parameters, and the εj are concept clauses, which take one of three forms:
1. Application of a previously defined concept, indicating a subset of the type parameters modeling it.
2. Signature of a type attribute, type function, or procedure that must exist for any types modeling the concept. A procedure signature takes the form f : T → T′, where T is the domain and T′ is the codomain. A type function signature takes the form ![]() , where the domain and codomain are concepts.
, where the domain and codomain are concepts.
3. Axiom expressed in terms of these type attributes, type functions, and procedures.
We sometimes include the definition of a type attribute, type function, or procedure following its signature in the second kind of concept clause. It takes the form ![]() for some expression
for some expression ![]() . In a particular model, such a definition could be overridden with a different but consistent implementation.
. In a particular model, such a definition could be overridden with a different but consistent implementation.
For example, this concept describes a unary functional procedure:

This concept describes a homogeneous functional procedure:

(∀F ![]() FunctionalProcedure) UnaryFunction(F)
FunctionalProcedure) UnaryFunction(F) ![]() HomogeneousFunction(F)
HomogeneousFunction(F)
An abstract procedure is parameterized by types and constant values, with requirements on these parameters.[6] We use function templates and function object templates. The parameters follow the template keyword and are introduced by typename for types and int or another integral type for constant values. Requirements are specified via the requires clause, whose argument is an expression built up from constant values, concrete types, formal parameters, applications of type attributes and type functions, equality on values and types, concepts, and logical connectives.[7]
Here is an example of an abstract procedure:
template<typename Op>
requires(BinaryOperation(Op))
Domain(Op) square(const Domain(Op)& x, Op op)
{
return op(x, x);
}
The domain values could be large, so we pass them by constant reference. Operations tend to be small (e.g., a function pointer or small function object), so we pass them by value.
Concepts describe properties satisfied by all objects of a type, whereas preconditions describe properties of particular objects. For example, a procedure might require a parameter to be a prime number. The requirement for an integer type is specified by a concept, while primality is specified by a precondition. The type of a function pointer expresses only its signature, not its semantic properties. For example, a procedure might require a parameter to be a pointer to a function implementing an associative binary operation on integers. The requirement for a binary operation on integers is specified by a concept; associativity of a particular function is specified by a precondition.
To define a precondition for a family of types, we need to use mathematical notation, such as universal and existential quantifiers, implication, and so on. For example, to specify the primality of an integer, we define
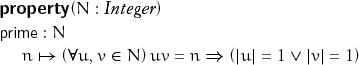
where the first line introduces formal type parameters and the concepts they model, the second line names the property and gives its signature, and the third line gives the predicate establishing whether the property holds for a given argument.
To define regularity of a unary functional procedure, we write
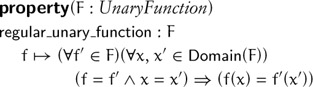
The definition easily extends to n-ary functions: Application of equal functions to equal arguments gives equal results. By extension, we call an abstract function regular if all its instantiations are regular. In this book every procedural argument is a regular function unless otherwise stated; we omit the precondition stating this explicitly.
Project 1.1 Extend the notions of equality, assignment, and copy construction to objects of distinct types. Think about the interpretations of the two types and axioms that connect cross-type procedures.
1.8 Conclusions
The commonsense view of reality humans share has a representation in the computer. By grounding the meanings of values and objects in their interpretations, we obtain a simple, coherent view. Design decisions, such as how to define equality, become straightforward when the correspondence to entities is taken into account.
