Chapter 8

Coordinates with Mutable Successors

This chapter introduces iterator and coordinate structure concepts that allow relinking:modifying successor or other traversal functions for a particular coordinate. Relinking allows us to implement rearrangements, such as sorting, that preserve the value of source at a coordinate. We introduce relinking machines that preserve certain structural properties of the coordinates. We conclude with a machine allowing certain traversals of a tree without the use of a stack or predecessor links, by temporarily relinking the coordinates during the traversal.

8.1 Linked Iterators

In Chapter 6 we viewed the successor of a given interator as immutable: Applying successor to a particular iterator value always returns the same result. A linked iterator type is a forward iterator type for which a linker object exists; applying the linker object to an iterator allows the successor of that iterator to be changed. Such iterators are modeled by linked lists, where relationships between nodes can be changed. We use linker objects rather than a single set_successor function overloaded on the iterator type to allow different linkings of the same data structure. For example, doubly linked lists could be linked by setting both successor and predecessor links or by setting successor links only. This allows a multipass algorithm to minimize work by omitting maintenance of the predecessor links until the final pass. Thus we specify concepts for linked iterators indirectly, in terms of the corresponding linker objects. Informally, we still speak of linked iterator types. To define the requirements on linker objects, we define the following related concepts:

Two ranges are disjoint if they include no iterator in common. For half-open bounded ranges, this corresponds to the following:

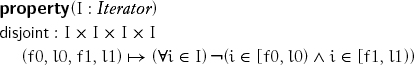
and similarly for other kinds of ranges. Since linked iterators are iterators, they benefit from all the notions we defined for ranges, but disjointness and all other properties of ranges can change over time on linked iterators. It is possible for disjoint ranges of forward iterators with only a forward linker—singly linked lists—to share the same limit—commonly referred to as nil.

8.2 Link Rearrangements

A link rearrangement is an algorithm taking one or more linked ranges, returning one or more linked ranges, and satisfying the following properties.

• Input ranges (either counted or bounded) are pairwise disjoint.
• Output ranges (either counted or bounded) are pairwise disjoint.
• Every iterator in an input range appears in one of the output ranges.
• Every iterator in an output range appeared in one of the input ranges.
• Every iterator in each output range designates the same object as before the rearrangement, and this object has the same value.

Note that successor and predecessor relationships that held in the input ranges may not hold in the output ranges.

A link rearrangement is precedence preserving if, whenever two iterators i j in an output range came from the same input range, i j originally held in the input range.

Implementing a link rearrangement requires care to satisfy the properties of disjointness, conservation, and ordering. We proceed by presenting three short procedures, or machines, each of which performs one step of traversal or linking, and then composing from these machines link rearrangements for splitting, combining, and reversing linked ranges. The first two machines establish or maintain the relationship f = successor(t) between two iterator objects passed by reference:

We can use advance_tail to find the last iterator in a nonempty bounded range:^[1]

We can use advance_tail and linker_to_tail together to split a range into two ranges based on the value of a pseudopredicate applied to each iterator. A pseudopredicate is not necessarily regular, and its result may depend on its own state as well as its inputs. For example, a pseudopredicate might ignore its arguments and return alternating false and true values. The algorithm takes a bounded range of linked iterators, a pseudopredicate on the linked iterator type, and a linker object. The algorithm returns a pair of ranges: iterators not satisfying the pseudopredicate and iterators satisfying it. It is useful to represent these returned ranges as closed bounded ranges [h, t], where h is the first, or head, iterator, and t is the last, or tail, iterator. Returning the tail of each range allows the caller to relink that iterator without having to traverse to it (using find_last, for example). However, either of the returned ranges could be empty, which we represent by returning h = t = l, where l is the limit of the input range. The successor links of the tails of the two returned ranges are not modified by the algorithm. Here is the algorithm:

The procedure is a state machine. The variables t0 and t1 point to the tails of the two output ranges, respectively. The states correspond to the following conditions:

s0: successor(t0) = f ¬p(t0)
s1: successor(t1) = f p(t1)
s2: successor(t0) = f ¬p(t0) p(t1)
s3: successor(t1) = f ¬p(t0) p(t1)

Relinking is necessary only when moving between states s2 and s3. goto statements from a state to the immediately following state are included for symmetry.

Lemma 8.1 For each of the ranges [h, t] returned by split_linked, h = l t = l.

Exercise 8.1 Assuming that one of the ranges (h, t) returned by split_linked is not empty, explain what iterator t points to and what the value of successor(t) is.

Lemma 8.2 split_linked is a precedence-preserving link rearrangement.

We can also use advance_tail and linker_to_tail to implement an algorithm to combine two ranges into a single range based on a pseudorelation applied to the heads of the remaining portions of the input ranges. A pseudorelation is a binary homogeneous pseudopredicate and thus not necessarily regular. The algorithm takes two bounded ranges of linked iterators, a pseudorelation on the linked iterator type, and a linker object. The algorithm returns a triple (f, t, l), where [f, l) is the half-open range of combined iterators, and t [f, l) is the last-visited iterator. A subsequent call to find_last(t, l) would return the last iterator in the range, allowing it to be linked to another range. Here is the algorithm:

Exercise 8.2 Implement combine_linked, allowing for empty inputs. What value should be returned as the last-visited iterator?

The procedure is also a state machine. The variable t points to the tail of the output range. The states correspond to the following conditions:

s0: successor(t) = f0 ¬r(f1, t)
s1: successor(t) = f1 r(t, f0)

Relinking is necessary only when moving between states s0 and s1.

Lemma 8.3 If a call combine_linked_nonempty(f0, l0, f1, l1, r, s) returns (h, t, l), h equals f0 or f1 and, independently, l equals l0 or l1.

Lemma 8.4 When state s2 is reached, t is from the original range [f0, l0), successor(t) = l0, and f1 ≠ l1; when state s3 is reached, t is from the original range [f1, l1), successor(t) = l1, and f0 ≠ l0.

Lemma 8.5 combine_linked_nonempty is a precedence-preserving link rearrangement.

The third machine links to the head of a list rather than to its tail:

With this machine, we can reverse a range of iterators:

To avoid sharing of proper tails, h should be the beginning of a disjoint linked list (for a singly linked list, nil is acceptable) or l. While we could have used l as the initial value for h (thus giving us reverse_linked), it is useful to pass a separate accumulation parameter.

8.3 Applications of Link Rearrangements

Given a predicate on the value type of a linked iterator type, we can use split_linked to partition a range. We need an adapter to convert from a predicate on values to a predicate on iterators:

With this adapter, we can partition a range into values not satisfying the given predicate and those satisfying it:

Given a weak ordering on the value type of a linked iterator type, we can use combine_linked_nonempty to merge increasing ranges. Again, we need an adapter to convert from a relation on values to a relation on iterators:

After combining ranges with this relation, the only remaining work is to find the last iterator of the combined range and set it to l1:

Lemma 8.6 If [f0, l0) and [f1, l1) are nonempty increasing bounded ranges, their merge with merge_linked_nonempty is an increasing bounded range.

Lemma 8.7 If i0 [f0, l0) and i1 [f1, l1) are iterators whose values are equivalent under r, in the merge of these ranges with merge_linked_nonempty, i0 i1.

Given merge_linked_nonempty, it is straightforward to implement a merge sort:

Lemma 8.8 sort_linked_nonempty_n is a link rearrangement.

Lemma 8.9 If is a nonempty counted range, sort_linked_nonempty_n will rearrange it into an increasing bounded range.

A sort on a linked range is stable with respect to a weak ordering r if, whenever iterators i j in the input have equivalent values with respect to r, i j in the output.

Lemma 8.10 sort_linked_nonempty_n is stable with respect to the supplied weak ordering r.

Exercise 8.3 Determine formulas for the worst-case and average number of applications of the relation and of the linker object in sort_linked_nonempty_n.

While the number of operations performed by sort_linked_nonempty_n is close to optimal, poor locality of reference limits its usefulness if the linked structure does not fit into cache memory. In such situations, if extra memory is available, one should copy the linked list to an array and sort the array.

Sorting a linked range does not depend on predecessor. Maintaining the invariant:

i = predecessor(successor(i))

requires a number of backward-linking operations proportional to the number of comparisons. We can avoid extra work by temporarily breaking the invariant. Suppose that I is a linked bidirectional iterator type, and that forward_linker and backward_linker are, respectively, forward and backward linker objects for I. We can supply forward_linker to the sort procedure—treating the list as singly linked—and then fix up the predecessor links by applying backward_linker to each iterator after the first:

Exercise 8.4 Implement a precedence-preserving linked rearrangement unique that takes a linked range and an equivalence relation on the value type of the iterators and that produces two ranges by moving all except the first iterator in any adjacent sequence of iterators with equivalent values to a second range.

8.4 Linked Bifurcate Coordinates

Allowing the modification of successor leads to link-rearrangement algorithms, such as combining and splitting. It is useful to have mutable traversal functions for other coordinate structures. We illustrate the idea with linked bifurcate coordinates.

For linked iterators, we passed the linking operation as a parameter because of the need to use different linking operations: for example, when restoring backward links after sort. For linked bifurcate coordinates, there does not appear to be a need for alternative versions of the linking operations, so we define them in the concept:

The definition space for set_left_successor and set_right_successor is the set of nonempty coordinates.

Trees constitute a rich set of possible data structures and algorithms. To conclude this chapter, we show a small set of algorithms to demonstrate an important programming technique. This technique, called link reversal, modifies links as the tree is traversed, restoring the original state after a complete traversal while requiring only constant additional space. Link reversal requires additional axioms that allow dealing with empty coordinates: ones on which the traversal functions are not defined:

traverse_step from Chapter 7 is an efficient way to traverse via bidirectional bifurcating coordinates but requires the predecessor function. When the predecessor function is not available and recursive (stack-based) traversal is unacceptable because of unbalanced trees, link reversal can be used to temporarily store the link to the predecessor in a link normally containing a successor, thus ensuring that there is a path back to the root.^[3]

If we consider the left and right successors of a tree node together with the coordinate of a previous tree node as constituting a triple, we can perform a rotation of the three members of the triple with this machine:

Repeated applications of tree_rotate allow traversal of an entire tree:

Theorem 8.1 Consider a call of traverse_rotating(c, proc) and any nonempty descendant i of c, where i has initial left and right successors l and r and predecessor p. Then

1. The left and right successors of i go through three transitions:

   

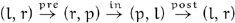
2. If n_r and n_r are the weights of l and r, the transitions 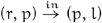and 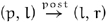take 3_nl + 1 and 3_nr + 1 calls of tree_rotate, respectively.
3. If k is a running count of the calls of tree_rotate, the value of k mod 3 is distinct for each of the three transitions of the successors of i.
4. During the call of traverse_rotating(c, proc), the total number of calls of tree_rotate is 3n, where n is the weight of c.

Proof: By induction on n, the weight of c.

Exercise 8.5 Draw diagrams of each state of the traversal by traverse_rotating of a complete binary tree with seven nodes.

traverse_rotating performs the same sequence of preorder, inorder, and postorder visits as traverse_nonempty from Chapter 7. Unfortunately, we do not know how to determine whether a particular visit to a coordinate is the pre, in, or post visit. There are still useful things we can compute with traverse_rotating, such as the weight of a tree:

We can also arrange to visit each coordinate exactly once by counting visits modulo 3:

Project 8.1 Consider using tree_rotate to implement isomorphism, equivalence, and ordering on binary trees.

8.5 Conclusions

Linked coordinate structures with mutable traversal functions allow useful rearrangement algorithms, such as sorting linked ranges. Systematic composition of such algorithms from simple machinelike components leads to efficient code with precise mathematical properties. Disciplined use of goto is a legitimate way of implementing state machines. Invariants involving more than one object may be temporarily violated during an update of one of the objects. An algorithm defines a scope inside which invariants may be broken as long as they are restored before the scope is exited.