Preface to Volume IV
Financial risk management is a relatively new discipline. It is driven internally by the need for optimal returns on risk-based capital and, ultimately, by the survival of the firm. External drivers include clients, who are typically risk averse, and industry regulators, whose objectives are to protect investors and to promote competition, although their ultimate concern is for financial stability in the global economy. In recent years market volatility has been rising as trading focuses on increasingly complex instruments whose risks are extremely difficult to assess. The origins of financial securities, futures and options go back several centuries, yet we are only just beginning to understand how to quantify the risks of complex financial products realistically, even though this makes all the difference between success and failure in the financial industry.
I liken the risk management profession as it stands today to that of medicine in the eighteenth century. Until this time general ill health in the population and continual outbreaks of uncontrolled diseases were met with ignorance, masked by mumbo-jumbo, in the medical profession. As a result average life expectancy was short and, for most, the quality of life was poor. But in the nineteenth century a number of comprehensive texts such as Gray's Anatomy1 began to educate the medical profession. Such is the knowledge we have acquired during the past two centuries that nowadays even a general practitioner must spend many years in training. Modern medical training is very demanding, but as a result people live longer and healthier lives.
Turmoil in the banking industry following a collapse of credit markets began soon after I finished writing the Market Risk Analysis series. In September 2008 the Treasury-Eurodollar (TED) spread (which in normal markets is about 5–10 basis points) exceeded 300 basis points, and it remains above 200 basis points at the time of writing. The value of stocks around the entire globe has fallen drastically and rapidly, reminiscent of the world stock market crash of 1929. To give the reader some idea of the extent of the losses: between the end of August and mid November 1929 the benchmark Dow Jones Industrial Average Index of 30 US blue chip stocks lost almost 50% of its value; from the end of April 2008 until the end of October 2008 it had lost almost 40% of its value. The US markets are not falling as much as stock markets in most other countries and the dollar is stronger now than it has been for many years. Several exchanges have suspended trading on more than one occasion, and even then several markets have crashed by more than 10% in a single day. The currencies of some emerging markets, such as the Korean wan, have plummeted in value against the US dollar. Markets in Europe have fallen more than 50% since the end of April, and some experts say further falls are imminent at the time of writing.
Why is this happening? And what is the likely effect on the financial system? These questions are not easy to answer, as the crisis is still ongoing at the time of writing. All the reasons for, and effects of, a catastrophe are usually revealed only after the event.
SUMMARY OF THE 2008 BANKING CRISIS
There is a trigger for all financial crises, and in this case the first crack appeared with the sub-prime mortgage crisis in the US. During the years 2004–2006 stock markets across the globe surged as the cost of credit reached all-time lows. New ways of securitizing loans meant that counterparty credit quality mattered little to the salesman on commission. European banks, and investors in countries where yields had been extremely low for years, flocked to buy collateralized debt obligations (CDO) and similar new products. The main sellers were the five largest investment banks: Goldman Sachs, Morgan Stanley, Merrill Lynch, Lehman Brothers and Bear Stearns. Even retail banks began to rely on securitizing their loans and short-term funding via the interbank market rather than on a deposit base.
Whenever there is uncertainty in a free market economy, this promotes a cycle in which optimism can lead to exuberance, followed by doubt and finally panic. The basic principle underlying the CDO is sound – after all, if the senior tranche of a mortgage-backed security corresponds to two-thirds of the whole and the recovery rate on defaulting mortgages is 50%, it would only be affected if more than two-thirds of the creditors defaulted! So we had reason to be optimistic in the mid 2000’s and there was a strong market for these new yield-enhancement vehicles. A fundamental problem was that their pricing lacked transparency. Because of the very considerable pricing model risk – the mark-to-model prices being crucially dependent on the assumptions made – doubts began to infiltrate the exuberance. And, as doubt turned to panic, the market dried up, so market prices became even more unreliable than the model prices. Given the mark-to-market accounting framework used by banks, a huge liquidity risk appeared in the trading book, and this was not covered by the bank's regulatory capital.
As liquidity fell out of the CDO market, banks turned to the interbank market to fund their liquidity gap. Because cash-rich banks demanded such high levels of collateral guarantees, other banks – and hedge funds, some of which were very highly leveraged – had great difficulty rolling over credit lines. Hedge funds were hit particularly hard. As the bull market turned, the values of their investments began to fall, and they had less collateral than usual to meet these larger guarantees. They have been forced to liquidate investments to meet collateral calls, increasing the downward pressure on stocks. The result was a crash in market prices across the globe during October 2008, with emerging stock markets and currencies being the worst hit, as US and European hedge funds liquidated their holdings in emerging markets.
The full extent of the current financial crisis first began to unfold in September 2008, with the failure of three of the five largest investment banks and of the US insurance giant AIG which, like the huge financial conglomerates Fannie Mae and Freddie Mac a few months before, was bailed out by the US government. Speculative short selling on the last two major investment banks, Goldman Sachs and Morgan Stanley, spread to the many retail banks in various countries that had been actively operating in capital markets since the repeal of the Glass-Steagall agreement in 1999,2 either buying CDOs or using proprietary trading in derivatives to boost profits. All three Icelandic banks defaulted, and with this some savers in other countries lost their capital. Then volatility in banking sector stocks spilled over into energy, commodities and related stocks, on fears of a falling demand for oil and raw materials with the onset of a global recession.
Eventually governments responded by increasing deposit protection, lowering interest rates and providing additional liquidity. As a last resort, schemes for partial nationalisation of banks have been proposed – schemes that include caps on the remuneration of executives and traders – along with bans on short selling to attempt to stem the slide in stock prices. Regulators disregarded anti-monopoly laws as distressed banks were taken over by large cash-rich retail banks. The banking sector has now moved towards oligopolistic competition, with a few huge conglomerates such as JP Morgan dominating the markets. Given the unthinkable threat of a collapse of the global banking system in which the general public lose their savings, most governments have now raised deposit insurance ceilings.
CAUSES AND EFFECTS OF THE CRISIS
A catalyst for this particular crisis was Alan Greenspan's policy of promoting US growth by keeping US interest rates low. After the Russian crisis in 1998 US treasury rates were also brought down, but as the market recovered interest rates were raised to prevent inflation increasing. During the technology crash in 2001 and 2002 US interest rates were brought down to about 1%, which encouraged increased consumption and promoted US exports, and thus revived the US economy. After the recovery started Greenspan did not raise interest rates quickly enough. There were no fears of inflation. Yet, every time interest rates are held too low for too long, it creates a bubble. This time the bubble was caused by an ‘easy credit’ environment, culminating in the ‘credit crunch’ which marked the beginning of the 2008 financial crisis.
The main factor underlying this financial crisis is the intrinsic instability in the banking system resulting from the lack of unified and intelligent principles for the accounting, regulation, and risk management of financial institutions. These principles have evolved separately in each framework, each without sufficient regard for the other two disciplines.
One of the major derivatives markets is driven by the different accounting frameworks used by banks and their clients. Differences between the principles of cost (or value) accounting used by non-financial companies on the one hand, and the mark-to-market (MtM) accounting used by banks in their trading books on the other hand, drives the market for interest rate swaps and their derivatives. Of course, companies will try to finance themselves by issuing bonds, but short term liquidity gaps are financed by taking loans from banks. Banks prefer to lend at a floating rate because this has very low risk in MtM accounting. On the other hand, floating rate notes and bonds have high risk in cost accounting, so companies prefer to take loans at fixed rates, which have low risk in cost accounting. Thus, banks double their business, issuing low risk notes and then offering interest rate swaps for floating into fixed rates. And, since fixed rates have high risk in MtM accounting, they use derivatives on interest rate swaps to hedge.
In relation to the underlying securities markets and in relation to world gross domestic product (GDP) the volume of financial derivatives traded is huge. At the end of 2007 the total notional outstanding on bond issues was about $80 trillion and the value of company stocks was about $40 trillion. Relatively few stock and bond holders hedge their positions because securities are often held by investors that hope to make a profit over the long term. Thus the notional size of the derivatives market required for investors to hedge is a small fraction of $120 trillion. Many companies involved with importing and exporting goods hedge their exposures to exchange rate fluctuations, and to rising interest rates. The size of these exposures is related to the value of all goods produced in the world economy. World GDP was about $75 trillion in 2007, so corporate hedging activities should amount to some small fraction of this. Thus the two hedging activities should result in a derivatives market with notional size being just a small fraction of $200 trillion. However, the total notional size of derivatives markets in 2007 was about $600 trillion.
Before the crisis, the daily average trading volume (DATV) on derivatives exchanges was about $2 trillion. Foreign exchange forward contracts had DATV of between $2 and $3 trillion, and other over-the-counter (OTC) derivatives trading amounted to about $1 trillion per day. Most of these contracts had a very fast turnover rate – in fact, the vast majority of futures contracts are held for just a few days. Average daily production of goods and services, as measured by world GDP, was about $0.3 trillion per day. So the DATV on derivatives was about twenty times greater than daily world GDP. Very approximately, about one-tenth of the volume traded is used for hedging. The remaining trades must be for speculative purposes.
Speculative traders include proprietary traders, hedge funds, companies making bets and day traders. They trade in capital markets for the purpose of making profits over a short-term horizon, which distinguishes them from investors, who buy-and-hold. Approximately half of the speculators in the derivatives markets are proprietary traders in banks.
When interest rates are cut banks turn to the capital markets to make profits by increasing the volume of their speculative trading. As a result, huge bonuses are often paid to successful proprietary traders and their managers. But why should banks bet with the money of their savers and their clients? Apart from the possibility that they may be better at speculation than ordinary investors, because of better information or cheaper access to markets,3 banks need to create a liquid market in order to price derivatives. Their market makers provide OTC derivatives, making money on the bid-ask spread, quoting prices that are based on the cost of hedging. So they need a liquid market for their hedging instruments, which include futures and options. We absolutely need speculative trading in options, because the volume of trading creates a market where there is no reliable theoretical price. A case in point is the CDO market. But we do not necessarily need speculative trading on futures, because we know how to calculate the fair price of a futures contract. One reason why there was approximately $25 trillion of speculative trades on futures last year is that senior managers and proprietary traders are being driven by greed to acquire huge bonuses. This is why the recent nationalisation deals for UK banks has included a clause for limiting remuneration.
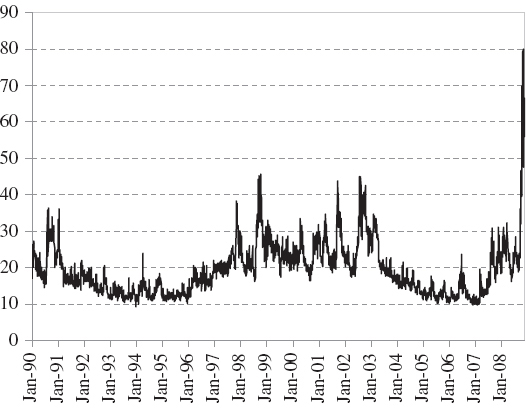
The Vix Volatility Index, January 1990 – October 2008
Proprietary trading by banks increases liquidity, but it may also increase volatility. Traditionally, banks are short volatility because investors want to be long volatility – it is an excellent diversification instrument. If there is no liquid market for volatility, banks will simply overcharge on the spread, which is one of the reasons why implied volatility usually exceeds historical volatility. The markets for variance swaps on European and US stock indices have been surging, making pure volatility a new, liquid asset. However, the informed banks would have temporarily stopped writing variance swaps at the onset of the banking crisis in mid September 2008, leaving only those in ignorance of the huge sums that could be lost on these positions to take the knock. Near the end of October 2008 the Vix jumped up to almost 80%, its highs during previous crises rarely exceeding 40%, as shown in the figure above, so the banks that sold variance swaps in September 2008 could have lost millions of dollars.4
WHAT COULD (OR SHOULD) HAPPEN NOW?
As this book goes to press many large banks are cutting down on their proprietary trading businesses, reducing the number of employees and the bonuses that are paid. If banks and their employees no longer have the incentive to use proprietary trading to increase profits, or if their trading is curtailed by regulators or governments, the size of the current OTC derivatives markets will dramatically reduce. Yet banks will always seek new ways to increase their profits. So new, unregulated and (probably) misunderstood markets, like the CDO market, will still be created.
Very often, the demand for and supply of derivatives arises from differences in accounting rules. For instance, the swaps market, which is the largest of all derivatives markets, is driven by differences between cost and market-to-market accounting. As long as we have no unified accounting framework for all market participants, new derivatives markets will be created. However, given the time it has taken to agree on accounting standards in IAS39,5 we should not expect much change in the near future.
This huge casino, in which many times world GDP is bet every year, has proved impossible to regulate. Regulators always respond to crises by tightening rules and increasing the minimum level of risk capital to be held by banks. But this exacerbates the problem, since the only way out of the current crisis is to create liquidity. Injecting taxpayers’ money into the capital markets is only a temporary solution; what is needed now is a complete reform of financial regulations. This does not necessarily mean tighter control on market operations, or increases in the minimum level of risk capital held by banks. Indeed, there may be government pressure to loosen regulation in order to establish a leading financial centre.
The new Basel Accord, which took eleven years to develop, failed to control the systemic risk in financial markets. And the reason it has failed is that regulators are too fixed on detailed calculations of value at risk in their ‘bottom-up’ regulatory capital framework. That is, they have been focusing on micro-managing the banks in their jurisdiction, and not on macro-financial decision making under uncertainty. What may be needed now, in addition to curtailing the proprietary trading by banks, is a top-down, differential system of capital charges, with the major banks that pose the greatest systemic threat holding proportionally higher capital reserves than minor banks.
This last spectacular failure in financial markets calls for a revision of the global banking system. This does not necessarily mean the wholesale nationalisation of banks, or even a return to socialist principles. That would indeed be an admission of failure, especially for Russia and the Eastern European countries that have only recently embraced capitalism. Free capital markets are essential to globalisation, and globalisation is essential for the health of the world's economy. To prevent the next crisis being even more critical that this one, an urgent reform of the accounting, regulation and risk management principles that underpin financial markets is required.
After each market crash – e.g. following the burst of the technology bubble in the early part of this decade, and following the Russian debt default in 1998 – governments try to promote growth by cutting interest rates and by injecting capital into the financial system. And, to be effective, each time they have to inject more capital and introduce more drastic cuts in interest rates than before. This is because the banking system is unstable, and markets have recovered only by sowing even deeper seeds for the next crisis. Unless drastic reforms of the system are made in the near future, even more drastic action will be required to resolve the next crisis, when it comes.
And what about financial risk management, and market risk management in particular – what reforms are needed now? A fundamental distinction must be drawn between risk managers and risk analysts. A good risk manager should be adept at making decisions under uncertainty, and for this he needs to be well-informed about the basic economic principles that underpin price formation in capital markets. And risk managers, like all managers, should be held accountable for their actions. Unfortunately, the opposite is usually the case. If a bank encounters problems due to bad management, then senior executives and directors can leave to join another firm, often with guaranteed bonuses on top of a six-figure salary.
Risk analysts and financial engineers – for whom these books are designed – use mathematical models to measure risk, and to price illiquid products using arbitrage pricing theory. The assumptions made by these models need constant testing and refining, so that superior models can be developed. With greater confidence in mark to model prices, and in portfolio risk assessment, it may be easier to stem the panic when the next crisis comes. Clearly, better education in quantitative risk analysis is the key to developing effective risk models and accurate pricing models for financial institutions.
Each financial crisis has a disastrous effect on the global economy, so the lives of ordinary people are adversely affected. I believe these crises can and will be avoided, but only when financial risk managers acquire the knowledge, skills and framework they really need to operate effectively in their profession. The recent crisis has shown that there is an urgent need for growth and change in the entire financial industry and in the financial risk management profession in particular.
An important and fundamental change must be to start educating risk analysts properly, so that their managers really understand the risks that banks and other financial institutions are taking, as far as this is possible. Risk is a mathematical concept: it is a measure of uncertainty. So risk managers or, at least, their trusted analysts, need to understand mathematics first, before they can even begin to understand risk.
There are two international financial risk management associations, the Professional Risk Managers’ International Association (PRMIA) and the Global Association of Risk Professionals (GARP).6 These associations provide entry-level qualifications for financial risk management. The PRM qualification is at a higher level than the FRM or the Associate PRM, but even the four exams for the full PRM qualification can be passed with only one year of part-time study.
In the UK medical doctors must undergo a minimum of 5 years’ full-time study, and to rise to senior positions they must take tough examinations every few years. Health risk management is so important to the economy that our National Health Service offers a regular programme of free vaccinations and free screenings for cancer, heart disease, and so forth. Why, then, have banks been treating financial risk management so casually, placing inappropriately qualified people in senior positions and taking less than adequate care over the education of their junior staff? Financial risk management is such a vast subject that to learn what we need to provide effective risk management in today's complex and volatile markets should take many years of full-time study, just as it does for medical doctors.
ABOUT THE MARKET RISK ANALYSIS SERIES
Sitting at my desk, writing this preface – the very last item on the agenda of the Market Risk Analysis series – I feel a huge sense of relief that the punishing work schedule I have been setting myself has nearly reached its conclusion. When I started out, five years ago, I did not intend to write four books. I just wanted to write one book: a book that describes all that a market risk analyst should know about building market value-at-risk (VaR) models; to explain everything in great detail so that readers came away with something they could actually use to educate themselves, without the need for formal courses. I also wanted to provide numerous practical examples, showing how to implement the theory that I cover in all types of financial markets. That is why I put every idea that I possibly could into a simple, interactive Excel workbook, with real financial data on equities, currencies, interest rates and commodities; this way, readers experience the idea ‘hands-on’, right from the start, and I truly believe this is a fantastic learning tool for an intelligent, self-motivated reader.7
I soon realized that in rising to this challenge I had set myself a very considerable task. To fully understand all aspects of market VaR as it is (or should be) used by major financial institutions today, the analyst needs to understand a good deal of mathematics, especially statistics and financial econometrics, as well as knowing about financial markets, the type of instruments traded in these markets, how to price them, why we hedge them and how to hedge them properly. It is a huge agenda – and this is just for the market risk analyst! As a result, there are numerous references to the earlier volumes of Market Risk Analysis in this book.
Please do not buy these books if you think you can be a financial risk analyst without understanding much mathematics. It is important to distinguish between risk management and risk analysis. Whilst I very often refer to risk management, this book series is called Market Risk Analysis, because it focuses on the mathematical modelling of market risks. A financial risk manager requires the same skills as any business manager, including a capacity for leadership, some knowledge of economics and of psychology and a superficial, not necessarily detailed, understanding of the technical side of the business. By contrast, the financial risk analyst's profession requires a very broad and in-depth knowledge of financial markets, finance theory, mathematics, statistics and econometrics.
One of the first developments in the financial risk management profession was to categorize risks into three broad types, labelled market, credit and operational risk. This was convenient because quite different techniques are used to assess each type of risk. My definition of market risk is the risk resulting from adverse moves in prices of liquid financial instruments. Market risk therefore includes credit spread risk, just as it includes interest rate risk. The probability of default affects credit spreads, so credit risk affects spread risk. But the scope of these books does not extend to credit risk analysis, just as monetary policy affects base interest rates but the theory of economic policy decision making is not within the scope of these books.
This book series is not, at least primarily, about the risk management of financial markets; it is called Market Risk Analysis, because it deals with market risk in the narrow sense, defined above, and when risk management (as opposed to risk analysis) is discussed it is market risk management, not credit or operational risk management. In particular, please do not buy these books if you want to learn about credit risk analysis, or about credit risk management, or about collateralized debt obligations and counterparty default. Neither should you buy these books if you want everything in one volume. At this level of detail, such a book would be more than 1500 pages long, and not easy to carry around with you. Also, there are separate markets for the earlier volumes in the series; not everyone in the finance industry wants to learn how to assess risk in a VaR framework.
Why did I write this book? To answer this fully I should first explain why I changed my agenda and wrote the precursors, starting with Volume I: Quantitative Methods in Finance. I started teaching mathematics to non-mathematicians over 20 years ago, and have continued to develop materials that allow intelligent students with relatively little quantitative background to undertake a fast-track course in mathematics that is oriented towards their specialism. For the past five years I have been teaching a course in Quantitative Methods for Finance to master's degree students at the ICMA Centre. In 10 weeks I need to bring students up to scratch in Excel as well as equipping them with the basic knowledge of calculus, linear algebra, statistics, econometrics and numerical methods, and how these subjects are used for financial applications. So each year I teach finance through mathematical applications in a very pedagogical way, sometimes in a single class with over 200 students having disparate quantitative backgrounds. I decided to write the first volume with two purposes in mind – as a set text for my Quantitative Methods for Finance course and similar courses (there are plenty) and to provide a fast-track route to intelligent, independent readers who want a succinct, targeted and pedagogical exposition of the mathematical knowledge required by a market risk analyst.
What about Volume II: Practical Financial Econometrics? When I was young I trained as an algebraist, developed only a passing interest in game theory, unfortunately, and at the time that my work focused on econometrics (because I had to teach it) I was drawn into financial econometrics by consultancy work. Thus, during the 1990s and well before most real academic econometricians discovered this veritable motorway into finance, I was accidentally positioned as one of the better known financial econometricians in the industry. Then I wrote Market Models – but this book is now over seven years old – so why not write a more rigorous, complete and up-to-date financial econometrics text for the Market Risk Analysis series? Volume II is primarily aimed at market risk professionals working in portfolio management or for hedge funds, students on Finance master's courses, and academic researchers. But a secondary purpose is that Volume II is required knowledge for all serious market risk analysts, and most of the material covered is pre-requisite for readers of this book, at least if they want to gain an in-depth understanding of advanced VaR models.
During the past few years I have developed research interests in continuous time finance: in volatility theory and in option pricing and hedging in particular. Volatility theory is a complex subject, and there are only a few texts in this area that are accessible to non-specialists. Believing that I could write a comprehensive and clear exposition of volatility theory, option pricing and hedging, I decided to augment the text for Volume III: Pricing, Hedging and Trading Financial Instruments to include interest rate sensitive instruments, futures and forwards, describing the markets but with an emphasis on the efficient pricing and hedging of portfolios containing such instruments. The final chapter of Volume III draws the previous chapters together by describing the mapping of portfolios of different classes of financial instruments; this way, Volume III lays the essential finance theory foundations for the VaR models that are described in this book.
Although the four volumes of Market Risk Analysis are very much interlinked, each volume serves a different purpose. Volume IV: Value-at-Risk Models could be adopted as a stand-alone text for an advanced course in Market Risk, but only for students who have already gained a good knowledge of quantitative methods, financial econometrics, finance theory, financial markets and financial instruments. Readers would benefit by working through the previous volumes before reading this one, or they may use the numerous cross-references to earlier volumes that are provided in the text. This requires a considerable investment of time and money. Although I hope that many university courses will adopt these books as core texts, my main purpose is to provide a self-study programme for readers wishing to gain a proper foundation for the job of market risk analysis. Dedicated and intelligent readers should be able to understand the material in all four books with one or two years of full-time study.
The aim of Market Risk Analysis is to define a syllabus for education in market risk analysis, from the basics to the most advanced level of understanding we have today, to set standards for the profession of market risk analyst, and to provide the means whereby the required skills may be attained. When I have time, I hope to develop a professional Market Risk Analyst qualification, with four exams based on each of these books and of a level equivalent to a challenging master's degree course.
The target readership for Market Risk Analysis, Volume IV: Value-at-Risk Models includes risk analysts in banks and finance-related firms such as software companies, insurance firms, investment companies and hedge funds; academics researching into market risk and/or forecasting with econometric models; and students on financial risk management master's courses. No other existing text on value at risk takes such a pedagogical and practical approach as this, at the same time as covering the theory both rigorously and comprehensively. Several theoretical results are new and each empirical application is unique.
Because I focus exclusively on market risk the most similar existing texts, at least in terms of broad content, are Dowd (2005) and Danielsson (2007). However, Dowd's book is mainly on the theory of market VaR, with relatively little on its practical implementation for realistic risk management problems, and Danielsson's book is shorter and far less detailed or comprehensive. Market Risk Analysis, Volume IV: Value-at-Risk Models is written at a quantitative level that is similar to Dowd (2005), Danielsson (2007) and Christoffersen (2003), higher than that of Jorion (2006) and lower than that of McNeil et al. (2005). It is more advanced and comprehensive, than Butler (1999). In so far as I place an equal emphasis on theory and practical implementation, this book could be compared with Holton (2003).
I would not be surprised if some readers react badly to the advanced level of understanding required for this book. The discipline of market risk analysis has existed for nearly two decades, but by publishing this book I am, in a sense, challenging the entire profession. In my view, a market risk analyst should be able to understand everything I have written, and more. If he cannot, he is simply not qualified for this seriously responsible job. On the other hand, an analyst who gains this understanding can look forward to a stimulating and rewarding career, as a return on the investment of substantial time and effort required to obtain a mastery of this material.
OUTLINE OF VOLUME IV
Chapter 1, Value at Risk and Other Risk Metrics, introduces the risk metrics that are commonly used by fund managers, banks and corporations. A market risk metric is a single number that captures the uncertainty in a portfolio's P&L, or in its return, summarizing the portfolio's potential for deviations from a target or expected return. Whilst VaR has become a universal risk metric used by banks and by non-financial corporations, fund managers have traditionally used quite different metrics. As well as tracking error and its limitations for use in active fund management, lower partial moments and VaR-based downside risk metrics such as benchmark VaR and expected shortfall are introduced. But VaR has some undesirable properties. It is not a coherent risk metric, unless we make some simplifying assumptions about the behaviour of the risk factors and the portfolio type. We explain why it is important to aggregate and disaggregate risks in the bottom-up risk assessment paradigm that is prevalent today, and introduce conditional, stand-alone, marginal and incremental VaR in a general mathematical framework. Empirical examples focus on the distinction between measuring VaR at the portfolio level and at the risk factor level, and the reason why we obtain different results when the same historical data are used in the three fundamental types of VaR model, i.e. parametric linear, historical and Monte Carlo VaR models.
Chapter 2, Parametric Linear VaR Models, is the longest chapter in the book. It covers the theory of parametric VaR models for linear portfolios in a rigorous mathematical framework, introducing several new results. We provide formulae for both VaR and expected tail loss (ETL) – which is also sometimes called conditional VaR – based on the assumptions that risk factor returns have a multivariate normal distribution, a Student t distribution and or a mixture of normal and/or Student t distributions. We also show how to use exponentially weighted moving average covariance matrices and how to scale VaR over different risk horizons when portfolio returns are autocorrelated. Thirty examples and several long case studies cover the aggregation and disaggregation of stand-alone and marginal VaR for large hedged and unhedged international portfolios containing interest rate sensitive instruments, equities and commodities, and each is supported with its own interactive Excel spreadsheet, usually based on real financial data.
Chapter 3, Historical Simulation, provides a critical introduction to the standard approach to measuring historical VaR and ETL. We address the need to measure historical VaR initially at the daily risk horizon, and the challenging problem of scaling VaR to longer risk horizons. Empirical examples motivate the need for volatility adjustment, and its extension to filtered historical simulation based on a generalized autoregressive conditional heteroscedasticity (GARCH) model. Again, numerous examples and case studies based on real financial data cover the practical implementation of historical VaR and ETL estimation, and its aggregation and disaggregation for portfolios containing interest rate sensitive instruments, equities and commodities and with foreign currency exposures. We explain how to improve the precision of VaR and ETL estimates at extreme quantiles, comparing the pros and cons of kernel fitting, Cornish – Fisher expansion, extreme value theory and fitting a Johnson SU distribution. Throughout this chapter we deal with linear portfolios, leaving the far more complex problem of measuring historical VaR and ETL for option portfolios to Chapter 5.
Chapter 4, Monte Carlo VaR, begins by reviewing some basic concepts in Monte Carlo simulation from univariate and multivariate distributions, including the generation of random numbers and variance reduction. However, fewer than 20 pages are devoted to this, and readers should not expect to cover the material in as much depth as textbooks that are exclusively concerned with simulation. The main focus of this chapter is a subject that has hitherto received little attention in the VaR literature: the need to provide a proper specification of the risk factor returns model when measuring Monte Carlo VaR. First we focus on building realistic dynamic models of individual risk factor returns, including volatility clustering and regime switching, and then we cover multivariate models, from multivariate normal i.i.d. processes to models with general parametric marginals with dependency captured by copulas. We also explain how to reduce the number of risk factors using principal component analysis. All of the complex models introduced are implemented in interactive Excel spreadsheets for a variety of real portfolios.
Chapter 5, Value at Risk for Option Portfolios, opens with a summary of the Taylor expansions that are used to map option portfolios to their main risk factors, and explains the likely effect on VaR estimates due to the size and magnitude of the different Greeks of a portfolio: specifically, these are termed delta, gamma, vega and theta effects. We take care to explain why these effects can be very different depending on whether we are estimating static VaR, which assumes the portfolio is not traded during the risk horizon, and dynamic VaR, where the portfolio is rebalanced daily over the risk horizon to return the risk factor sensitivities to their original level. Static VaR is suitable for estimating the risk of a single structured product that is not intended to be dynamically rebalanced, and dynamic VaR is useful for assessing risk when traders are at their limits. The main focus of this chapter is the practical implementation of both historical and Monte Carlo VaR models for option portfolios, evaluated both exactly and with risk factor mapping. Starting with simple, unhedged positions, the practical examples become increasingly complex, including VaR estimates for option portfolios with several underlyings and path-dependent claims.
Chapter 6, Risk Model Risk, covers the reasons why different VaR methodologies give different results and the statistical methods used to assess the accuracy of VaR estimates. There are many sources of error in VaR and ETL estimates. In equity and option portfolios even the risk factor mapping can be a very significant source of model risk, and quite different VaR estimates can result when we change the risk factors, or the data used to estimate the risk factor sensitivities, or the statistical methodology used for factor sensitivity estimation. In all portfolios it is the specification of the risk factor returns model that is the most significant source of model risk, and many empirical examples are provided to support this. After deriving theoretical results on confidence intervals for VaR estimates, the main focus of this chapter is on the VaR and ETL backtesting methodology. Starting with the simple backtests suggested by banking regulators, we describe unconditional and conditional coverage tests, regression-based backtests, ETL backtests based on standardized exceedance residuals, bias statistics and distribution forecasts. Throughout this section of the chapter, we illustrate the practical implementation of all these backtests in Excel workbooks using two different VaR and ETL estimates for a simple position on the S&P 500 index.
Chapter 7, Scenario Analysis and Stress Testing, opens by challenging the validity of historical data for estimating VaR and ETL, except over very short risk horizons. We maintain that using historical data itself implies a subjective view (that history will repeat itself) and that other beliefs or personal subjective views of senior management and the board of directors can and should be used in a mathematically coherent model of risk. Beginning with a description of how different types of beliefs about future market behaviour can be incorporated into VaR and ETL estimation, we argue that the traditional stress-testing framework that aims to quantify a ‘worst case’ loss is totally meaningless. So, whilst the standard stress testing methods such as ‘factor push’ are both described and illustrated, we focus on a coherent stress testing framework based on what I call ‘distribution scenarios’. The last section of the chapter focuses on the use of historical or hypothetical stressed covariance matrices, stress tests based on principal components and on GARCH volatility clustering, and endogenous and exogenous liquidity adjustments to VaR.
Chapter 8, Capital Allocation, covers the application of VaR and ETL to regulatory and economic capital allocation. Beginning with the basic differences between banking and trading book accounting, we cover the minimum market risk capital requirements for banks under the 1996 Amendment to the first Basel Accord, describing and illustrating both the internal models approach and the standardized rules. After the new Basel II Accord, in the wake of the credit crunch that began in 2007, the Basel Committee suggested a new incremental risk charge for credit spread and equity risks, applied to internal models that have specific risk recognition. We provide empirical examples to illustrate how banks might choose to calculate this new add-on to the capital charge. The second half of the chapter opens with a description of the measurement and applications of economic capital, having particular emphasis on aggregation risk. We then introduce the most common types of risk adjusted performance measures for economic capital allocation, and provide empirical examples in Excel on the optimal allocation of economic capital under various constraints.
ABOUT THE CD-ROM
This book emphasizes teaching through practical examples supported by transparent Excel spreadsheets. Whenever it is possible to illustrate a model or a formula using a practical example – however simple or complex – I do this using Excel. This volume alone contains 62 Excel workbooks (each with several spreadsheets, some of which are fairly complex) covering all the examples and figures in the text, and 16 case studies that implement VaR models in practice. These may be found on the accompanying CD-ROM. The data can be used by tutors or researchers since they were obtained from free internet sources, and references for updating are provided. Also the graphs and tables can be modified if required, and copied into lectures notes based on this book. Within these spreadsheets readers may change any parameters of the problem (the parameters are indicated in red) and see the new solution (the output is indicated in blue). Rather than using VBA code, which will be obscure to many students, I have encoded the formulae directly into the spreadsheet. Thus the reader need only click on a cell to read the formula. The interactive spreadsheets are designed to offer tutors the possibility to set, as exercises for their courses, an unlimited number of variations on the examples in the text.
I hope you will find these examples and case studies useful. A great variety of problems have been illustrated, from the simple estimation of VaR at the portfolio level using basic forms of each VaR model, to advanced methodologies such as filtered historical simulation with adjustments for volatility and correlation clustering, or Monte Carlo VaR using copulas and non-normal marginals, applied at the risk factor level and disaggregated into stand-alone and marginal VaR components due to different risk factor classes.
ACKNOWLEDGEMENTS
An unkind Amazon reviewer once suggested that I only write books to make money. This is absurd, not only because if I wanted to increase my income I could have accepted many financially attractive invitations during the last five years instead of devoting my time to these books. I write mainly because I enjoy it; and also because I imagine that I have something to offer. However, when all is said and done, if readers appreciate these books, that is all to the good; and if they do not, I would have written them anyway.
The Market Risk Analysis series would never have been completed if I had been unable to hold to a strong purpose, which is to do whatever I can to further the financial risk management profession. In this respect it has been a pleasure to work with individuals whose tireless efforts to raise standards and form a truly global financial risk management network I very much admire. Of these I would like to say a special thank-you to David Koenig, who set up the PRMIA organization in which I play an active role, and to Elizabeth Sheedy, my co-editor, co-author, co-researcher and close friend.
I would like to express my thanks to all the individuals who have helped in the production and marketing of this series: to Sam Whittaker for her unerring faith in my judgement when one book turned into four; to Caitlin Cornish for her solid editorial decisions and Aimee Dibbens for her efficient handling of numerous issues; to Louise Holden for her energetic marketing support and Lori Boulton for her tireless, ongoing attempts to manage Amazon sites; to Richard Leigh for his careful copy-editing; to Viv Wickham and her excellent team in production; and especially to Philippe Derome and Ronnie Barnes, who contacted me whilst reading the earlier volumes in this series and volunteered their meticulous proof reading before the publication of this one. I know from experience that I can rely on their knowledge and intelligent, careful reading to detect many errors and that the book will be much improved by their work.
But most of all, I would like to thank my family – and my children Boris and Helen, in particular – who are only 20 and 12 respectively at the time of writing. For five crucial years of their lives they have shared their mother with another purpose. Maybe this has not been easy for them, but their unerring love and understanding during these long years has been the most valuable support of all.
Discussion forums and other resources for the Market Risk Analysis series are available at www.marketriskanalysis.com.
1 See http://en.wikipedia.org/wiki/Gray's_Anatomy.
2 The Glass-Steagall agreement of 1933 was named after the two US senators who proposed it in response to the 1929 stock market crash. Under this agreement retail banks and commercial banks were depository taking institutions, and only investment banks traded in capital markets, to create secondary markets for the bond issues they underwrote. The agreement was repealed in 1999, allowing retail and commercial banks to trade in capital markets, but investment banks were still not allowed to take deposits. The net effect of this asymmetry was that retail and commercial banks were better funded than investment banks. In September 2008 Goldman Sachs and Morgan Stanley were granted the status of ‘bank holding companies’, allowing them to take deposits. So, the distinction between retail and commercial banks on the one hand, and investment banks on the other, is disintegrating.
3 For instance, Salomon Brothers used to make the market for US junk bonds, so they could see the entire market and take positions accordingly.
4 Vix is the implied volatility index of the S&P 500 index.
5 These standards were developed by the International Accounting Standards Board. See http://www.iasb.org.
6 See www.prmia.org and www.garp.com.
7 I have constructed 140 Excel workbooks for the examples, figures, tables and case studies in this series. That is about 1500 spreadsheets in total. Phew!
