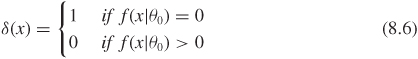8
Admissibility
In this chapter we will explore further the concept of admissibility. Suppose, following Wald, we agree to look at long-run average loss R as the criterion of interest for choosing decision rules. R depends on θ, but a basic requirement is that one should not prefer a rule that does worse than another no matter what the true θ is. This is a very weak requirement, and a key rationality principle for frequentist decision theory. There is a similarity between admissibility and the strict coherence condition presented in Section 2.1.2. In de Finetti’s terminology, a decision maker trading a decision rule for another that has higher risk everywhere could be described as a sure loser—except for the fact that the risk difference could be zero in some “lucky” cases.
Admissible rules are those that cannot be dominated; that is, beaten at the risk game no matter what the truth is. Admissibility is a far more basic rationality principle than minimax in the sense that it does not require adhering to the “ultra-pessimistic” perspective on θ. The group of people willing to take admissibility seriously is in fact much larger than those equating minimax to frequentist rationality. To many, therefore, characterization of sets of admissible decision rules has been a key component of the contribution of decision theory to statistics.
It turns out that just by requiring admissibility one is drawn again towards an expected utility perspective. We will discover that to generate an admissible rule, all one needs is to find a Bayes rule. The essence of the story is that a decision rule cannot beat another everywhere and come behind on average. This needs to be made more rigorous, but, for example, it is enough to require that the Bayes rule be unique for it to work out. A related condition is to rule out “know-it-all” priors that are not ready to change in the light of data. This general connection between admissibility and Bayes means there is no way to rule out Bayes rules from the standpoint of admissibility, even though admissibility is based on long-run performance over repeated experiments.
Even more interesting from the standpoint of foundations is that, in certain fairly big classes of decision problems, all admissible rules are Bayes rules or limiting cases of the Bayes rule. Not only can the chief frequentist rationality requirement not rule any Bayesian out, but also one has to be Bayesian (or close) to satisfy it in the first place! Another way to think about this is that no matter what admissible procedure one may concoct, somewhere behind the scenes, there is a prior (or a limit of priors) for which that is the expected utility solution. A Bayesian perspective brings that into the open and contributes to a more forthright scientific discourse.
Featured articles:
Neyman, J. & Pearson, E. S. (1933). On the problem of the most efficient test of statistical hypotheses, Philosophical Transaction of the Royal Society (Series A) 231: 286–337.
This feature choice is a bit of a stretch in the sense that we do not dwell on the Neyman–Pearson theory at all. However, we discover at the end of the chapter that the famed Neyman–Pearson lemma can be reinterpreted as a complete class theorem in the light of all the theory we developed so far. The Neyman–Pearson theory was the spark for frequentist decision theory, and this is a good place to appreciate its impact on the broader theory.
There is a vast literature on the topics covered in this chapter, which we only briefly survey. More extensive accounts and references can be found in Berger (1985), Robert (1994), and Schervish (1995).
8.1 Admissibility and completeness
If we take the risk function as the basis for comparison of two decision rules δ and δ′, the following definition is natural:
Definition 8.1 (R-better) A decision rule δ is called R-better than another decision rule δ′ if
and R(θ, δ) < R(θ, δ′) for some θ. We also say that δ dominates δ′.
Figure 8.1 shows an example. If two rules have the same risk function they are called R-equivalent.
If we are building a toolbox of rules for a specific decision problem, and δ is R-better than δ′, we do not need to include δ′ in our toolbox. Instead we should focus on rules that cannot be “beaten” at the R-better game. We make this formal with some additional definitions.
Definition 8.2 (Admissibility) A decision rule δ is admissible if there is no R-better rule.
Figure 8.1 Risk functions for decision rules δ and δ′. Here δ dominates δ′: the two risk functions are the same for θ close to 1 but the risk of δ is lower near 0 and never greater.
Referring back to Figure 7.2 from Chapter 7, a5 is R-better than a6, which is therefore not admissible. On the other hand, a4 is admissible as long as only nonrandomized actions are allowed, even though it could never be chosen as the optimum under either principle. When randomized rules are allowed, it becomes possible to decrease losses from y4 in both dimensions, and a4 becomes inadmissible. It is true that Figure 7.2 talks about losses and not risk, but loss is a special case of risk when there are no data available.
In general, admissibility will eliminate rules but will not determine a unique winner. For example, in Figure 7.2, there are five admissible rules among nonrandomized ones, and infinitely many admissible randomized rules. Nonetheless admissibility has two major strengths that place it in a strategic position in decision theory: it can be used to rule out decision rules, or entire approaches, as inconsistent with rational behavior; and it can be used to characterize broad families of rules that are sure to include all possible admissible rules. This is implemented via the notion of completeness, a property of classes of decision rules that ensures that we are not leaving out anything that could turn out to be useful.
Definition 8.3 (Completeness) We give three variants:
A class D of decision rules is complete if, for any decision rule δ ∊ D, there is a decision rule δ′ ∊ D which is R-better than δ.
A class D of decision rules is essentially complete if, for any decision rule δ ∉ D, there is a decision rule δ′ ∊ D such that R(θ, δ′) ≤ R(θ, δ) for all θ; that is, δ′ is R-better or R-equivalent to δ.
A class D of decision rules is said to be minimal (essentially) complete if D is complete and if no proper subset of D is (essentially) complete.
From this definition it follows that any decision rule δ that is outside of a complete class is inadmissible. If the class is essentially complete, then a decision rule δ that is outside of the class may be admissible, but one can find a decision δ′ in the class with the same risk function. Thus, it seems reasonable to restrict our attention to a complete or essentially complete class.
Complete classes contain all admissible decision rules, but they may contain inadmissible rules as well. A stronger connection exists with minimal complete classes: these classes are such that, if even one rule is taken out, they are no longer complete.
Theorem 8.1 If a minimal complete class exists, then it coincides with the class of all admissible decision rules.
We left the proof for you (Problem 8.3).
Complete class results are practical in the sense that if one is interested in admissible strategies, one can safely restrict attention to complete or essentially complete classes and study those further. The implications for foundations are also far reaching. Complete class results are useful for characterizing statistical approaches at a higher level of abstraction than single decision rules. For example, studying the class of all tests based on a threshold of the likelihood ratio, one can investigate the whole Neyman–Pearson theory from the point of view of rationality. For another example, we can explore whether it is necessary to use randomized decision rules:
Theorem 8.2 If the loss function L(θ, a) is convex in a, then the class of non-randomized decision rules D is complete.
We left this proof for you as well (Problem 8.8).
8.2 Admissibility and minimax
Unfortunately for minimax aficionados, this section is very short. In general, to prove admissibility of minimax rules it is best to hope they are close enough to Bayes or limiting Bayes and use the theory of the next section. This will not always be the case: a famously inadmissible minimax rule is the subject of Chapter 9.
On the flip side, a very nice result is available for proving minimaxity once you already know a rule is admissible.
Theorem 8.3 If δM has constant risk and it is admissible, then δM is the unique minimax rule.
Problem 8.11 asks you to prove this and is a useful one to quickly work out before reading the rest of the chapter.
For an example, say x is a Bin(n, θ) and
Consider the rule δ*(x) = x/n. The risk function is
that is δ* has constant risk. With a little work you can also show that δ* is the unique Bayes rule with respect to a uniform prior on (0, 1). Lastly, using the machinery of the next section we will be able to prove that δ* is admissible. Then, using Theorem 8.3, we can conclude that it is minimax.
8.3 Admissibility and Bayes
8.3.1 Proper Bayes rules
Let us now consider more precisely the conditions for the Bayes rules to be admissible. We start with the easiest case, when Θ is discrete. In this case, a sufficient condition is that the prior should not completely rule out any of the possible values of θ.
Theorem 8.4 If Θ is discrete, and the prior π gives positive probability to each element of Θ, then the Bayes rule with respect to π is admissible.
Proof: Let δ* be the Bayes rule with respect to π, and suppose, for a contradiction, that δ* is not admissible; that is, there is another rule, say δ, that is R-better than δ*. Then R(θ, δ) ≤ R(θ, δ*) with strict inequality R(θ0, δ) < R(θ0, δ*) for some θ0 in Θwith positive mass π(θ0) > 0. Then,
This contradicts the fact that δ* is Bayes. Therefore, δ* must be admissible.
Incidentally, from a subjectivist standpoint, it is a little bit tricky to accept the fact that there may even be points in a discrete Θ that do not have a positive mass: why should they be in Θ in the first place if they do not? This question opens a well-populated can of worms about whether we can define Θ independently of the prior, but we will close it quickly and pretend, for example, that we have a reasonably objective way to define Θ or that we can take Θ to be the union of the supports over a group of reasonable decision makers.
An analogous result to Theorem 8.4 holds for continuous θ, but you have to start being careful with your real analysis. An easy case is when π gives positive mass to all open sets and the risk function is continuous. See Problem 8.10. The plot of the proof is very similar to that used in the discrete parameter case, with the difference that, to reach a contradiction, we need to use the continuity condition to create a lump of dominating cases with a strictly positive prior probability.
Another popular condition for guaranteeing admissibility of Bayes rules is uniqueness.
Theorem 8.5 Any unique Bayes estimator is admissible.
The proof of this theorem is left for you as Problem 8.4. To see the need for uniqueness, look at Problem 8.9.
Uniqueness is by no means a necessary condition: the important point is that when there is more than one Bayes rule, all Bayes rules share the same risk function. This happens for example if two Bayes estimators differ only on a set S such that Pθ(S) = 0, for all θ.
Theorem 8.6 Suppose that every Bayes rule with respect to a prior distribution, π, has the same risk function. Then all these rules are admissible.
Proof: Let δ* denote a Bayes rule with respect to π and R(θ, δ*) denote the risk of any such Bayes rule. Suppose that there exists δ0 such that R(θ, δ0) ≤ R(θ, δ) for all θ and with strict inequality for some θ. This implies that
Because δ* is a Bayes rule with respect to π, the inequality must be an equality and δ0 is also a Bayes rule with risk R(θ, δ*), which leads to a contradiction.
8.3.2 Generalized Bayes rules
Priors do not sit well with frequentists, but being able to almost infallibly generate admissible rules does. A compromise that sometimes works is to be lenient on the requirement that the prior should integrate to one. We have seen an example in Section 7.7. A prior that integrates to something other than one, including perhaps infinity, is called an improper prior. Sometimes you can plug an improper prior into Bayes’ rule and get a proper posterior-like distribution, which you can use to figure out the action that minimizes the posterior expected loss. What you get out of this procedure is called a generalized Bayes rule:
Definition 8.4 If π is an improper prior, and δ* is an action which minimizes the posterior expected loss Eθ|x[L(θ, δ(x))], for each x with positive predictive density m(x), then δ* is a generalized Bayes rule.
For example, if you are estimating a normal mean θ, with known variance, and you assume a prior π(θ) = 1, you can work out the generalized Bayes rule to be 
. This is also the maximum likelihood estimator, and the minimum variance unbiased estimator. The idea of choosing priors that are vague enough that the Bayes solution agrees with common statistical practice is a convenient and practical compromise in some cases, but a really tricky business in others (Bernardo and Smith 1994, Robert 1994). Getting into details would be too much of a digression for us now. What is more relevant for our discussion is that a lot of generalized Bayes rules are admissible.
Theorem 8.7 If Θ is a subset of ℜk such that every neighborhood of every point in Θ intersects the interior of Θ, R(θ, δ) is continuous in θ for all δ, the Lebesgue measure on Θ is absolutely continuous with respect to π, δ* is a generalized Bayes rule with respect to π, and L(θ, δ*(x))f(x|θ) is ν × π integrable, then δ* is admissible.
See Schervish (1995) for the proof. A key piece is the integrability of L times f, which gives a finite Bayes risk r. The other major condition is continuity. Nonetheless, this is a very general result.
Example 8.1 (Schervish 1995, p. 158) Suppose x is a Bin(n, θ) and θ ∊ Θ = A = [0, 1]. The loss is L(θ, a) = (θ – a)2 and the prior is π(θ) = 1/[θ(1 – θ)], which is improper. We will show that δ(x) = x/n is admissible using Theorem 8.7. There is an easier way which you can learn about in Problem 8.6.
The posterior distribution of θ, given x, is Beta(x, n – x). Therefore, for x = 1, 2, ..., n – 1, the (generalized) Bayes rule is δ*(x) = x/n, that is the posterior mean. Now, if x = 0,
which is finite only if δ*(x) = 0. Similarly, if x = n,
which is finite only if δ*(x) = 1. Therefore, δ*(x) = x/n is the generalized Bayes rule with respect to π. Furthermore,
has prior expectation 1/n. Therefore, δ* is admissible. If you are interested in a general characterization of admissible estimators for this problem, read Johnson (1971).
The following theorem from Blyth (1951) is one of the earliest characterizations of admissibility. It provides a sufficient admissibility condition by relating admissibility of an estimator to the existence of a sequence of priors using which we obtain Bayes rules whose risk approximates the risk of the estimator in question. This requires continuity conditions that are a bit strong: in particular the decision rules with continuous risk functions must form a complete class. We will return to this topic in Section 8.4.1.
Theorem 8.8 Consider a decision problem in which Θ has positive Lebesgue measure, and in which the decision rules with continuous risk functions form a complete class. Then an estimator δ0 (with a continuous risk function) is admissible if there exists a sequence 
of (generalized) priors such that:
r(πn, δ0) and
are finite for all n, where 
is the Bayes rule with respect to πn;for any nondegenerate convex set C ⊂ Θ, there exists a positive constant K and an integer N such that, for n ≥ N,
.
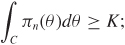
Proof: Suppose for a contradiction that δ0 is not admissible. Then, there must exist a decision rule δ′ that dominates δ0, and therefore a θ0 such that R(θ0, δ′) < R(θ0, δ0). Because the rules with continuous risk functions form a complete class, both δ0 and δ′ have a continuous risk function. Thus, there exists ε1 > 0, ε2 > 0 such that
R(θ, δ0) – R(θ, δ′) > ε1,
for θ in an open set C = {θ ∊ Θ : |θ – θ0| <2}.
From condition 1, 
, because 
is a Bayes rule with respect to πn. Thus, for all n ≥ N,
from condition 2. That r(πn, δ0)–r(πn, δn) ≥ ε1K is in contradiction with condition 3. Thus we conclude that δ0 must be admissible.
Example 8.2 To illustrate the application of this theorem, we will consider a simplified version of Blyth’s own example on the admissibility of the sample average for estimating a normal mean parameter. See also Berger (1985, p. 548). Suppose that x ~ N(θ, 1) and that it is desired to estimate θ under loss L(θ, a) = (θ – a)2. We will show that δ0(x) = x is admissible. A convenient choice for πn is the unnormalized normal density
πn(θ) = (2π)−1/2 exp(–0.5θ2/n).
The posterior distribution of θ, given x, is N(xn/(n + 1), n/(n + 1)). Therefore, with respect to πn, the generalized Bayes decision rule is 
, that is the posterior mean.
For condition 1, observe that
Therefore,
Here 
is the normalizing constant of the prior. Similarly,
Thus, we obtain that
For condition 2,
as long as C is a nondegenerate convex subset of Θ. Note that when C = ℜ, K = 1. The sequence of proper priors N(0, 1/n) would not satisfy this condition.
Finally, for condition 3 we have
Therefore, δ0(x) = x is admissible.
It can be shown that δ0(x) = x is admissible when x is bivariate, but this requires a more complex sequence or priors. We will see in the next chapter that the natural generalization of this result to three or more dimensions does not work. In other words, the sample average of samples from a multivariate normal distribution is not admissible.
A necessary and sufficient admissibility condition based on limits of improper priors was established later by Stein (1955).
Theorem 8.9 Assume that f(x|θ) is continuous in θ and strictly positive over Θ. Moreover, assume that the loss function L(θ, a) is strictly convex, continuous, and such that for a compact subset E ⊂ Θ,
An estimator δ0 is admissible if and only if there exists a sequence {Fn} of increasing compact sets such that Θ = ∪nFn, a sequence {πn} of finite measures with support Fn, and a sequence 
of Bayes estimators associated with πn such that:
there exists a compact set E0 ⊂ Θ such that infn πn(E0) ≥ 1;
if E ⊂ Θ is compact, supn πn(E) < +∞;
;
.
Stein’s result is stated in terms of continuous losses, while earlier ones we looked at were based on continuous risk. The next lemma looks at conditions for the continuity of loss functions to imply the continuity of the risk.
Lemma 3 Suppose that Θ is a subset of ℜm and that the loss function L(θ, a) is bounded and continuous as a function of θ, for all a ∊ A. If f(x|θ) is continuous in θ, for every x, the risk function of every decision rule δ is continuous.
The proof of this lemma is in Robert (1994, p. 239).
8.4 Complete classes
8.4.1 Completeness and Bayes
The results in this section relate the concepts of admissibility and completeness to Bayes decision rules and investigate conditions for Bayes rules to span the set of all admissible decision rules and thus form a minimal complete class.
Theorem 8.10 Suppose that Θ is finite, the loss function is bounded below, and the risk set is closed from below. Then the set of all Bayes rules is a complete class, and the set of admissible Bayes rules is a minimal complete class.
For a proof see Schervish (1995, pp. 179–180). The conditions of this result mimic the typical game-theoretic setting (Berger 1985, chapter 5) and are well illustrated by the risk set discussion of Section 7.5.1. The Bayes rules are also rules whose risk functions are on the lower boundary of the risk set.
Generalizations of this result to parameter sets that are general subsets of ℜm require more work. A key role is played again by continuity of the risk function.
Theorem 8.11 Suppose that A and Θ are closed and bounded subsets of the Euclidean space. Assume that the loss function L(θ, a) is a continuous function of a for each θ ∊ Θ, and that all decision rules have continuous risk functions. Then the Bayes rules form a complete class.
The proof is in Berger (1985, p. 546).
Continuity of the risk may seem like a restrictive assumption, but it is commonly met and in fact decision rules with continuous risk functions often form a complete class. An example is given in the next theorem. An important class of statistical problems is those with the monotone likelihood ratio property, which requires that for every θ1 < θ2, the likelihood ratio
is a nondecreasing function of x on the set for which at least one of the densities is nonzero. For problems with monotone likelihood ratio, and continuous loss, we only need to worry about decision rules with finite and continuous risk:
Theorem 8.12 Consider a statistical decision problem where X, Θ, and A are subsets of ℜ with A being closed. Assume that f(x|θ) is continuous in θ and it has the monotone likelihood ratio property. If:
L(θ, a) is a continuous function of θ for every a ∊ A;
L is nonincreasing in a for a ≤ θ and nondecreasing for a ≥ θ; and
there exist two functions K1 and K2 bounded on the compact subsets of Θ × Θ such that
L(θ1, a) ≤ K1(θ1, θ2)L(θ2, a) + K2(θ1, θ2), ∀ a ∊ A,
then decision rules with finite and continuous risk functions form a complete class.
For proofs of this theorem see Ferguson (1967) and Brown (1976).
8.4.2 Sufficiency and the Rao–Blackwell inequality
Sufficiency is one of the most important concepts in statistics. A sufficient statistic for θ is a function of the data that summarizes them in such a way that no information concerning θ is lost. Should decision rules only depend on the data via sufficient statistics? We have hinted at the fact that Bayes rules automatically do that, in Section 7.2.3. We examine this issue in more detail in this section. This is a good time to lay out a definition of sufficient statistic.
Definition 8.5 (Sufficient statistic) Let x ~ f(x|θ). A function t of x is said to be a sufficient statistic for θ if the conditional distribution of x, given t(x) = t, is independent of θ.
The Neyman factorization theorem shows that t is sufficient whenever the likelihood function can be decomposed as
See, for example, Schervish (1995), for a discussion of sufficiency and this factorization.
Bahadur (1955) proved a very general result relating sufficiency and rationality. Specifically, he showed under very general conditions that the class of decision functions which depend on the observed sample only through a function t is essentially complete if and only if t is a sufficient statistic. Restating it more concisely:
Theorem 8.13 The class of all decision rules based on a sufficient statistic is essentially complete.
The proof in Bahadur (1955) is hard measure-theoretic work, as it makes use of the very abstract definition of sufficiency proposed by Halmos and Savage (1949).
An older, less general result provides a constructive way of showing how to find a rule that is R-better or R-equivalent than a rule that depends on the data via statistics that are not sufficient.
Theorem 8.14 (Rao–Blackwell theorem) Suppose that A is a convex subset of ℜm and that L(θ, a) is a convex function of a for all θ ∊ Θ. Suppose also that t is a sufficient statistic for θ, and that δ0 is a nonrandomized decision rule such that Ex|θ[|δ0(x)|] < ∞. The decision rule defined as
is R-equivalent to or R-better than δ0.
Proof: Jensen’s inequality states that if a function g is convex, then g(E[x]) ≤ E[g(x)]. Therefore,
and
R(θ, δ1) |
= Et|θ[L(θ, δ1(t))] |
|
≤ Et|θ[Ex|t[L(θ, δ0(x))]] |
|
= Ex|θ[L(θ, δ0(x))] |
|
= R(θ, δ0) |
completing the proof.
This result does not say that the decision rule δ1 is any good, but only that it is no worse than the δ0 we started with.
Example 8.3 (Schervish 1995, p. 153). Suppose that x1, ..., xn are independent and identically distributed as N(θ, 1) and that we wish to estimate the tail area to the left of c – θ with squared error loss
L(θ, a) = (a – Θ(c – θ))2.
Here c is some fixed real number, and a ∊ A ≡ [0, 1]. A possible decision rule is the empirical tail frequency
It can be shown that 
is a sufficient statistic for θ, for example using equation (8.2). Since A is convex and the loss function is a convex function of a,
because x1|t is N(t,[n – 1]/n).
Because of the Rao–Blackwell theorem, the rule δ1(t) = Ex|t[δ0(x)] is R-better than δ0. In this case, the empirical frequency does not make any use of the functional form of the likelihood, which is known. Using this functional form we can bring all the data to bear in estimating the tail probability and come up with an estimate with lower risk everywhere. Clearly this is predicated on knowing for sure that the data are normally distributed. Using the entire set of data to estimate the left tail would not be as effective if we did not know the parametric form of the sampling distribution.
8.4.3 The Neyman–Pearson lemma
We now revisit the Neyman–Pearson lemma (Neyman and Pearson 1933) from the point of view of complete class theorems. See Berger (1985) or Schervish (1995) for proofs of the theorem.
Theorem 8.15 (Neyman–Pearson lemma) Consider a simple versus simple hypothesis testing problem with null hypothesis H0:θ = θ0 and alternative hypothesis H1:θ = θ1. The action space is A = {a0, a1} where ai denotes accepting hypothesis Hi (i = 0, 1). Assume that the loss function is the 0 – KL loss, that is a correct decision costs zero, while incorrectly deciding ai costs KL.
Tests of the form
where 0 ≤ γ (x) ≤ 1 if 0 < K < ∞ and γ(x) = 0 if K = 0, together with the test
(corresponding to K = ∞ above), form a minimal complete class of decision rules. The subclass of such tests with γ (x) ≡ γ (a constant) is an essentially complete class.
For any 0 ≤ α ≤ α*, there exists a test δ of the form (8.5) or (8.6) with α0(δ) = α and any such test is a most powerful test of size α (that is, among all tests δ with α0(δ) ≤ α such a test minimizes α1(δ)).
With this result we have come in a complete circle: the Neyman–Pearson theory was the seed that started Wald’s statistical decision theory; minimal completeness is the ultimate rationality endorsement for a statistical approach within that theory—all and only the rules generated by the approach are worth considering. The Neyman–Pearson tests are a minimal complete class. Also, for each of these tests we can find a prior for which that test is the formal Bayes rule. What is left to argue about?
Before you leave the theater with the impression that a boring happy ending is on its way, it is time to start looking at some of the results that have been, and are still, generating controversy. We start with a simple one in the next section, and then devote the entire next chapter to a more complicated one.
8.5 Using the same α level across studies with different sample sizes is inadmissible
An example of how the principle of admissibility can be a guide in evaluating the rigor of common statistical procedures arises in hypothesis testing. It is common practice to use a type I error probability α, say 0.05, across a variety of applications and studies. For example, most users of statistical methodologies are prepared to use α = 0.05 irrespective of the sample size of the study. In this section we work out a simple example that shows that using the same α in two studies with different sample sizes—all other study characteristics being the same—results in an inadmissible decision rule.
Suppose we are interested in studying two different drugs, A and B. Efficacy is measured by parameters θA and θB. To seek approval, we wish to test both H0A: θA = 0 versus H1A: θA = θ1 and H0B: θB = 0 versus H1B: θB = θ1 based on observations sampled from populations f(x|θA) and f(x|θB) that differ only in the value of the parameters. Suppose also that the samples available from the two populations are of sizes nA < nB.
The action space is the set of four combinations of accepting or rejecting the two hypotheses. Suppose the loss structure for this decision problem is the sum of the two drug specific loss tables
|
θA = 0 |
θA = θ1 |
|
|
θB = 0 |
θB = θ1 |
a0A |
0 |
L0 |
|
a0B |
0 |
L0 |
a1A |
L1 |
0 |
|
a1B |
L1 |
0 |
where L0 and L1 are the same for both drugs. This formulation is similar to the multiple hypothesis testing setting of Section 7.5.2. Adding the losses is natural if the consequences of the decisions apply to the same company, and also make sense from the point of view of a regulatory agency that controls the drug approval process.
The risk function for any decision function is defined over four possible combinations of values of θA and θB. Consider the space of decision functions δ = (δA(xA), δB(xB)). These rules use the two studies separately in choosing an action. In the notation of Section 7.5.1, αδ and βδ are the probabilities of type I and II errors associated with decision rule δ. So the generic decision rule will have risk function
θA |
θB |
R(θ, δ) |
0 |
0 |
L1αδA + L1αδB |
0 |
1 |
L1αδA + L0βδB |
1 |
0 |
L0βδA + L1αδB |
1 |
1 |
L0βδA + L0βδB |
Consider now the decision rule that specifies a fixed value of α, say 0.05, and selects the rejection region to minimize β subject to the constraint that α is no more than 0.05. Define β(α, n) to be the resulting type II error. These rules are admissible in the single-study setting of Section 7.5.1. Here, however, it turns out that using the same α in both δA(xA) and δB(xB) is often inadmissible. The reason is that the two studies have the same loss structure. As we have seen, by specifying α one implicitly specifies a trade-off between type I and type II error—which in decision-theoretic terms is represented by L1/L0. But this implicit relationship depends on the sample size. In this formulation we have an additional opportunity to trade-off errors with one drug for errors in the other to beat the fixed α strategy no matter what the true parameters are.
Taking the rule with fixed α as the starting point, one is often able to decrease α in the larger study, and increase it in the smaller study, to generate a dominating decision rule. A simple example to study is one where the decrease and the increase cancel each other out, in which case the overall type I error (the risk when both drugs are null) remains α. Specifically, call δ the fixed α = α0 rule, and δ′ the rule obtained by choosing α0 + ε in study A and α0 – ε in study B, and then choosing rejection regions by minimizing type II error within each study. The risk functions are
θA |
θB |
R(θ, δ) |
R(θ, δ′) |
0 |
0 |
2L1α0 |
2L1α0 |
0 |
1 |
L1α0 + L0β(α0, nA) |
L1(α0 + ε) + L0β(α0 + ε, nA) |
1 |
0 |
L1α0 + L0β(α0, nB) |
L1(α0 – ε) + L0β(α0 – ε, nB) |
1 |
1 |
L0(β(α0, nA) + β(α0, nB)) |
L0(β(α0 + ε, nA) + β(α0 – ε, nB)) |
If the risk of δ′ is strictly less than that of δ in the (0, 1) and (1, 0) states, then it turns out that it will also be less in the (1, 1) state. So, rearranging, sufficient conditions for δ′ to dominate δ are
These conditions are often met. For example, say the two populations are N(θA, σ2) and N(θB, σ2), where the variance σ2, to keep things simple, is known. Then, within each study
When θ1/σ = 1, nA = 5, and nB = 20, choosing ε = 0.001 gives
which is satisfied over a useful range of loss specifications.
Berry and Viele (2008) consider a related admissibility issue framed in the context of a random sample size, and show that choosing α ahead of the study, and then choosing the rejection region by minimizing type II error given n after the study is completed, leads to rules that are inadmissible. In this case the risk function must be computed by treating n as an unknown experimental outcome. The mathematics has similarities with the example shown here, except there is a single hypothesis, so only the (0, 0) and (1, 1) cases are relevant. In the single study case, the expected utility solution specifies, for a fixed prior and loss ratio, how the type I error probability should vary with n. This is discussed, for example, by Seidenfeld et al. (1990b), who show that for an expected utility maximizer, dαn/dn must be constant with n. Berry and Viele (2008) show how varying α in this way can dominate the fixed α rule. See also Problem 8.5.
In Chapter 9, we will discuss borrowing strength across a battery of related problems, and we will encounter estimators that are admissible in single studies but not when the ensemble is considered and losses are added. The example we just discussed is similar in that a key is the additivity of losses, which allows us to trade off errors in one problem with errors in another. An important difference, however, is that here we use only data from study A to decide about drug A, and likewise for B, while in Chapter 9 will will also use the ensemble of the data in determining each estimate.
8.6 Exercises
Problem 8.1 (Schervish 1995) Let Θ = (0, ∞), A = [0, ∞), and loss function L(θ, a) = (θ – a)2. Suppose also that x ~ U(0, θ), given θ, and that the prior for θ is the U(0, c) distribution for c > 0. Find two formal Bayes rules one of which dominates the other. Try your hand at it before you look at the solution below. What is the connection between this example and the Likelihood Principle? If x < c, should it matter what the rule would have said in the case x > c? What is the connection with the discussion we had in the introduction about judging an answer by what it says versus judging it by how it was derived?
Solution
After observing x < c, the posterior distribution is
while if x ≥ c the posterior distribution is defined arbitrarily. So the Bayes rules are of the form
which is the posterior mean, if x < c. Let 
denote the Bayes rule which has δ*(x) = c for x ≥ c. Similarly, define the Bayes rule 
which has δ*(x) = x for x ≥ c. The difference in risk functions is
Problem 8.2 Suppose T is a sufficient statistic for θ and let 
be any randomized decision rule in D. Prove that, subject to measurability conditions, there exists a randomized decision rule 
, depending on T only, which is R-equivalent to 
.
Problem 8.3 Prove that if a minimal complete class D exists, then it is exactly the class of all admissible estimators.
Problem 8.4 Prove Theorem 8.5.
Problem 8.5 (Based on Cox 1958) Consider testing H0: θ = 0 based on a single observation x. The probabilistic mechanism generating x is this. Flip a coin: if head draw an observation from a N(θ, σ = 1); if tail from a N(θ, σ = 10). The outcome of the coin is known. For a concrete example, imagine randomly drawing one of two measuring devices, one more precise than the other.
Decision rule δc (a conditional test) is to fix α = 0.05 and then reject H0 if x > 1.64 when σ = 1 and x > 16.4 when σ = 10. An unconditional test is allowed to select the two rejection regions based on properties of both devices. Show that the uniformly most powerful test of level α = 0.05 dominates δc.
There are at least two possible interpretations for this result. The first says that the decision-theoretic approach, as implemented by considering frequentist risk, is problematic in that it can lead to violating the Likelihood Principle. The second argues that the conditional test is not a rational one in the first place, because it effectively implies using a different loss function depending on the measuring device used. Which do you favor? Can they both be right?
Problem 8.6 Let x be the number of successes in n independent trials with probability of success θ ∊ (0, 1). Show that a rule is admissible for the squared error loss
L(θ, a) = (a – θ)2
if and only if it is admissible for the “standardized” squared error loss
Is this property special to the binomial case? To the squared error loss? State and prove a general version of this result. The more general it is, the better, of course.
Problem 8.7 Take x ~ N(θ,1), θ ~ N(0, 1), and
L(θ, a) = (θ – a)2e3θ2/4.
Show that the formal Bayes rule is δ*(x) = 2x and that it is inadmissible. The reason things get weird here is that the Bayes risk r is infinite. It will be easier to think of a rule that dominates 2x if you work on Problem 8.6 first.
Problem 8.8 Prove Theorem 8.2.
Problem 8.9 Let x be the number of successes in n = 2 independent trials with probability of success θ ∊ [0, 1]. Consider estimating θ with squared error loss. Say the prior is a point mass at 0. Show that the rule
δ*(0) = 0, δ*(1) = 1, δ*(2) = 0
is a Bayes rule. Moreover, show that it is not the unique Bayes rule, and it is not admissible.
Problem 8.10 If π gives positive mass to all open sets and the risk function is continuous, then the Bayes rule with respect to this prior is admissible.
Problem 8.11 Prove that if δM has constant risk and it is admissible, then δM is the unique minimax rule.