8

Another Look at Some Famous Numbers

In the preceding chapter we examined several of the most important numerical constants appearing in mathematics. The best known of these “famous numbers” are, of course, π (the ratio of the circumference and diameter of a circle) and e (the base of natural logarithms). We also looked briefly at three other important numbers: ø (the golden ratio), γ (Euler's constant), and δ (the Feigenbaum number).

In this chapter, the subject of famous numbers is continued but aimed in a somewhat different direction. We begin with what are called real numbers, imaginary numbers, and complex numbers. First, some rules are given for procedures such as the addition of complex numbers—so-called vector addition. Then a very interesting equation, originally given by Leonhard Euler, is introduced to generate some remarkable relationships involving real and imaginary numbers, including the one presented in the opening paragraph of the previous chapter. Using the methods of complex number addition, and calling on some things we know about π and e, we construct a polygonal spiral which we then use wickedly to strangle a negative number.

Finally, suppose you had to make a quick decision regarding a gift from your wealthy uncle. Which would you rather receive from him: 4³ dollars or 3⁴ dollars? Expressing this question in general terms and assuming that a is larger than b, which is the greater quantity: a^b or b^a?

Numbers: Real, Imaginary, and Complex

We start with a very simple algebraic equation: x² – 1 = 0. What is its solution? Easy: We move the 1 to the other side of the equation to get x² = + 1 and then take the square root of both sides. This yields . However, don't forget that it also yields x = – 1, because (– 1) × (– 1) = + 1. So the solution to this little equation is .

Fair enough. Now suppose we start with another very simple equation: x² + 1 = 0. Moving the 1 to the other side gives the expression x² = –1, and taking the square root yields x = . What in the world does mean? Well, this is called an “imaginary” number; it may or may not be a good name but we're stuck with it. Very simply, an imaginary number is the square root of a negative number. For hundreds of years, mathematicians did not know how to handle imaginary numbers, though nowadays they present no particular difficulties. Indeed, in many areas of mathematics, imaginary numbers are extremely useful quantities. The letter i has been adopted as the symbol for imaginary numbers. That is, . Furthermore, an entire methodology has been developed to handle arithmetical and algebraic manipulations involving imaginary numbers.

For example, consider the following equation: z₁ = + 5 – 2i. In this expression, the + 5 is called a real number. On the other hand, the –2i is termed an imaginary number because it contains the quantity i. The indicated sum, z₁ is called a complex number.

Now consider another equation: z₂ = – 3 + 4i. Suppose we want to add z₁ and z₂. To do this, we simply add the real numbers of the two equations and then add the imaginary numbers of the two equations. In our example, this operation yields the equation z₁ + z₂ = + 2 + 2i. All this is shown graphically in figure 8.1, in which the real numbers are plotted along the x-axis and the imaginary numbers are plotted along the y-axis. The z = x + iy plane is called the complex plane. We sometimes refer to z₁ and z₂ as vectors. We have just carried out a simple example of vector addition. We can also perform vector subtractions, multiplications, and divisions. The display shown in figure 8.1 is sometimes called an Argand diagram.

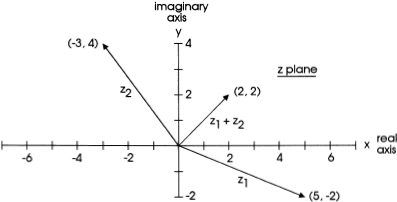
FIG. 8.1

An example of vector addition. z₁ = 5 – 2i, z₂ = – 3 + 4i, so z₁ + z₂ = 2 + 2i. This plot is an Argand diagram.

For use in an example we shall look at in a moment, we summarize the immediately preceding analysis. In a rectangular (x, y) coordinate system we plot real numbers in the plus or minus x-direction depending on whether they are positive or negative quantities. In the same way, we plot imaginary numbers in the plus or minus y-direction depending on whether they are positive or negative quantities. What could be simpler? Incidentally, a suggested reference for an elementary presentation of various topics concerning imaginary and complex numbers is Gardner (1992).

Some Amazing Mathematical Relationships

In 1746, that incredibly prolific mathematical genius named Leonhard Euler presented the following identity:

in which cos θ is the real part and sin θ is the imaginary part of the complex equation. As we shall now see, this equation yields some really amazing relationships.

Amazing Relationship 1

Let θ = π (i.e., 180°) in equation (8.1). Then since cos π = – 1 and sin π = 0, equation (8.1) gives

This is an extremely remarkable result. Here is an equation that uniquely relates the five most important numbers in all of mathematics: e, i, π, 1, and 0.

Amazing Relationship 2

Let θ = π/2 (i.e., 90°) in equation (8.1). Then since cos(π/2) = 0 and sin(π/2) = 1, we get e^iπ/2 = i. Multiplying the exponents of both sides of this equation by i yields e^–π/2 = iⁱ. Since e^–π/2 = 0.2079, we obtain the very remarkable result that iⁱ = 0.2079. This relationship says that i raised to the ith power is equal to a real number. Totally crazy! How can this possibly be? This is much too weird to even think about.

How to Strangle a Negative Number

We are now going to strangle the number – 1, and here is how we are going to do it. First, the following is a generalization of the infinite series given by equation (7.6):

Next, from equation (8.2) we get the relationship e^iπ = – 1. So if we substitute θ = iπ into equation (8.3) we obtain

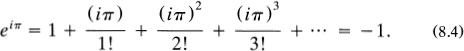
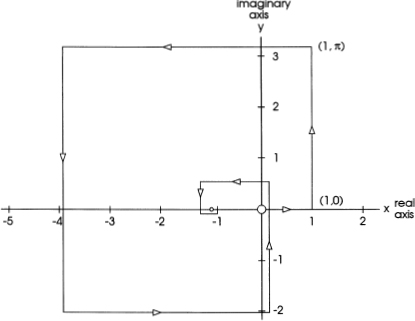
FIG. 8.2

The polygonal spiral created by vector addition of the infinite-series form of e^iπ. Note that the spiral converges on the point (– 1, 0).

Now remember that . Therefore i² = – 1, i³ = – i, i⁴ = + 1, i⁵ = + i, i⁶ = – 1, and so on. Substituting these values into equation (8.4) yields

We now prepare a graphical display of this equation, following the rules we presented and utilized in constructing figure 8.1, in which we simply added z₁ and z₂. The results of this exercise in vector addition are shown in figure 8.2. The angles at the corners of the resulting polygon are all 90°. The lengths of the sides are 1, π, π²/2, π³/6, π⁴/24, and so on. The coordinates of the first two corners are indicated in the figure; the others are easily calculated.

The graphical plot of figure 8.2 should be clear. As a result of the repeated vector addition, our “polygonal spiral” gets closer and closer to the point (– 1, 0) and eventually “strangles” the point. The total length of the spiral, without regard to the direction of the vectors, is simply L = e^π = 23.1407.

Which Is Larger: a^b or b^a?

In the preceding section, it was established that the total length of our “polygonal spiral” was e^π = 23.1407. Now, we are no longer interested in the previous topics such as complex numbers and vector diagrams. We are interested only in the quantity e^π = 23.1407. Suppose we switch the positions of π and e and then compute π^e. Recall that π = 3.14159 and e = 2.71828. With our hand calculator we determine that π^e = 22.4591, which is a bit less than e^π = 23.1407. Interesting, but so what?

Well, let's generalize. Suppose that a and b are positive numbers, not necessarily integers, and that a is larger than b. We ask the question: which is the larger quantity, a^b or b^a, that is, a to the bth power or b to the ath power? Incidentally, this problem was suggested by two somewhat similar problems that appear in Dörrie (1965) and Dunn (1980).

To start with, here are three numerical examples:

1. If a = 3 and b = 2, then a^b = 3² = 9 and b^a = 2³ = 8. In this case, a^b > b^a.

2. If a = 4 and b = 2, then a^b = 4² = 16 and b^a = 2⁴ = 16. In this case, a^b = b^a.

3. If a = 5 and b = 2, then a^b = 5² = 25 and b^a = 2⁵ = 32. In this case, a^b < b^a.

We note that modest changes in the magnitude of a, with the value of b held constant in these three examples, entirely alter the relative magnitudes of a^b and b^a. This seems strange.

It will be very helpful in our analysis if we know when the two quantities, a^b and b^a, are equal. That is,

Unfortunately, it is impossible to obtain a solution to this equation in a form that expresses a in terms of b or vice versa. Consequently, we must settle for a parametric solution. Taking the logarithms of both sides of equation (8.6) gives

We let a = kb, where k is a number larger than one (since a > b); k is called the parameter. Substituting this relationship into equation (8.7) and carrying out some algebra, we obtain the expressions

Assigning various numerical values to the parameter k in these expressions gives the magnitudes of a and b that satisfy equation (8.6).

An interesting question is, what are the values of a and b when k approaches one? We note that the relationships of equation (8.8) are indeterminate for k = 1. Never mind. In these two expressions, we make the substitution n = 1 /(k - 1). This yields

It is clear that if k = 1 then n = ∞. Utilizing equation (7.5), it is easily established that in this limiting (k = 1) case we have the values a = e and b = e.

The results of our analysis are displayed in figure 8.3. For your information, table 8.1 lists some coordinates for the curve a^b = b^a shown in the figure. Two interesting observations: (1) The values a = 4, b = 2 are the only integers for which a^b = b^a. (2) The values a = e, b = e, as the end point (k = 1) coordinates on the a^b = b^a curve, represent an unexpected appearance of our very remarkable number e.

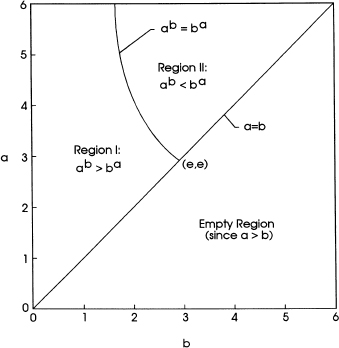
FIG. 8.3

Graphical display of the regions in which a^b is greater than, equal to, and less than b^a.

TABLE 8.1

The main feature of the display of figure 8.3 is the identification of region I in which a^b > b^a and region II where a^b < b^a. You might want to confirm these results by computation with some selected values for a and b, including a = π and b = e. Also, you will undoubtedly want to show that the slope of the a^b = b^a curve at the point (e, e) is (da/db) = –1, i.e., it is perpendicular to the line a = b.