14

More Great Turtle Races: Logarithmic Spirals

More turtle racing: This time we shall use several or many turtles and instruct all of them to move at the same speed. So it is not really racing; as we shall see, it is more a matter of symmetrical pursuit.

We start with a configuration involving two turtles. Turtle A is located at the west end of a straight line of length a, facing east. Turtle B is at the east end facing west. When the starting gun is fired, each turtle heads directly toward the other. Obviously, the two turtles will collide at the midpoint of the line and each will have covered a distance a/2.

Since that was not too difficult we move on to the three-turtle problem. This is not as easy. As shown in figure 14.1, initially the turtles are at the corners of an equilateral triangle with side length a. Turtle A is facing turtle B who is facing turtle C who is facing turtle A. Again, as the race commences, each turtle always heads directly toward his target.

The salient features of our analysis are that the three turtles will always be separated by an angle α = 120° = 2π/3 radians and will always be equidistant from the origin, r. We utilize the positions and paths of A and B for our analysis; by symmetry, the behavior of C will be the same.

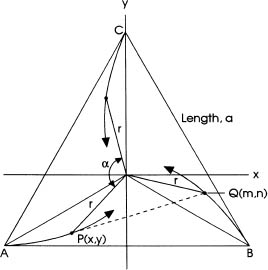
FIG. 14.1

Definition sketch for the three-turtle problem.

Expressing the coordinates (x, y) of point P and (m, n) of point Q in terms of the angles θ_A and θ_B, we establish the relationships

The criterion to “…always head directly toward…” is

Substituting (14.1) into (14.2) yields the differential equation

This equation is easily solved with the substitution y = wx. Carrying out some algebra and simple integrations, we obtain

where k is an integration constant. This expression can be written in polar coordinate form by substituting and θ = arctan(y/x):

To determine the value of the constant K, we employ the initial condition for either A, B, or C. Selecting the last, we have when θ = 90° = π/2 radians. This gives the answer:

or in final form

As we know, this is the equation of the logarithmic or equiangular spiral. In chapter 9, we learned that this beautiful curve makes its appearance in many places in nature. In hydrodynamics, for example, the logarithmic spiral is produced when a vortex flow is combined with a source or sink flow—like the spiral you get when you drain the bathtub. Numerous properties of this interesting curve are discussed by Lockwood (1961), by Steinhaus (1969), and by Thompson (1961).

Back to the three turtles. Their paths are shown in figure 14.2. Here's a good question: How far does each turtle go before it collides with the others at the center of the triangle? To answer this question we write the expression

where ds is an incremental length along the turtles' path and dr and dθ are incremental changes in r and θ. From this relationship we obtain the expression

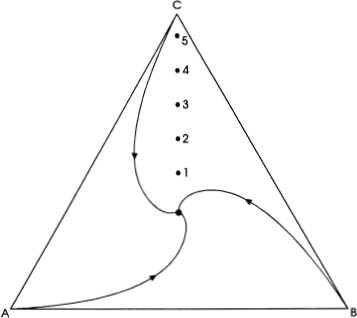
FIG. 14.2

Paths of the turtles in the three-turtle problem.

Using (14.6) in (14.8), we find the length of the travel path, S = (2/3)a. Thus, each turtle travels a distance equal to two-thirds of the length of the triangle's side. If a = 1.0 m = 100 cm and υ = 1.0 cm/s, the turtles will meet at the center of the triangle in T = S/υ = 66.7 s.

The obvious next problem concerns four turtles and a square. In this case, it is not difficult to show that the turtle paths are described by the equation

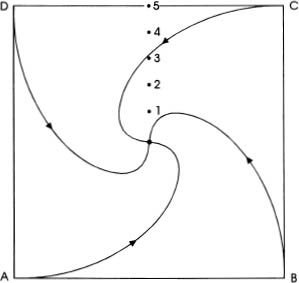
FIG. 14.3

Paths of the turtles in the four-turtle problem.

and the length of the path is S = a. Collision time is 100 seconds. This case is shown in figure 14.3.

Let us move on to five turtles and a pentagon, six turtles and a hexagon, eight turtles and an octagon, and n turtles and an n-gon. The general case solution is

in which α = 2π/n and n is the number of sides of the n-gon; θ₀ is a constant whose value is determined by the geometry of the initial condition.

The length of the path for the general case is

where in each instance a is the length of a side of the n-gon.

As the number of sides increases, the central angle, α = 2π/n, decreases. Utilizing the approximations sin α = α and cos α = 1 – α²/2, equation (14.10) becomes

and (14.11) reduces to

These approximations are valid for values of n larger than about 10.

As we increase the number of sides, our n-gon begins to look like a circle. So for very large n the quantity na is the circumference of a circle of radius r₀. That is, C = na = 2πr₀. In this case, setting θ₀ = 0, since now it does not matter where we start on the circle, equation (14.12) becomes

and from (14.13) the total length of a path is

Are you ready for the great experiment? We applied for and received a government grant to carry out an experiment featuring 360 small turtles spaced at 1° intervals around the circumference of a circle of radius r₀ = 10 m. Each turtle has instructions to head directly toward the turtle immediately ahead and to move at a speed υ = 1.0 cm/s.

Backing up briefly, we can establish that one of the properties of the logarithmic spiral is that it always intersects the radius vector r at a constant angle β. In our turtle problem we determine that this intersect angle β = α/2, where α = 2π/n is the central angle. For example, if n = 3, then α = 2π/3 and β = π/3 radians = 60°. If n = 4, then α = π/2 and β = π/4 radians = 45°.

In our great experiment, n = 360, and so α = π/180 and β = π/360 radians = 0.5°. Consequently, in our 360-gon, which is almost but not quite a circle, each turtle heads 0.5° inboard from the tangent to the equivalent circle.

Since we have a large value of n, equations (14.14) and (14.15) can be utilized. From (14.14) we see that r = r₀ = 10 m when θ = 0. If θ = 2π radians = 360° (i.e., one complete revolution of marching turtles around the circle), we determine that r = 9.466 m. Thus, the turtle circle has shrunk by about 53.4 centimeters after one revolution. In this first circuit they traveled approximately 61.6 m; since their speed is υ = 1.0 cm/s, it took them 6,120 seconds or around 1 hour and 42 minutes for the first lap.

The second lap takes a bit less time since the circle is slightly smaller. The third lap is shorter still, and so on. From equation (14.15) we determine that the total distance traveled by each turtle to get to the center is S = 1,146 m and it takes 31 hours and 50 minutes to get there. We prefer to ignore what happens when 360 tired turtles all arrive at r = 0 at the same instant—a pretty nasty traffic pileup.

There is one feature in common in all of the preceding problems: the turtles are pursuing one another on plane surfaces. An interesting generalization of our turtle problem is given by Aravind (1994), in which the plane surface is replaced by a spherical surface (constant positive curvature) and by a hyperbolic (or pseudosphere) surface (constant negative curvature).

A final word regarding a recommended reference. Virtually all of the topics covered in our book are examined in a clear and concise way in the comprehensive volume by Gellert et al. (1977). If you have a serious interest in the study of mathematics, this excellent reference book should be in your personal library.