7
A Brief Look at π, e, and Some Other Famous Numbers
The professor went to the board one day
And asked his class, just for the fun
What is the only conceivable way
To combine e, i, π, zero and one?
A brilliant young scholar, he proved quite a hero
Who knew the professor just loved to tease
Replied: eiπ + 1 = 0
Then he requested: the next question, please.
Many years ago, the writer received a magnificent $15 for submitting this poem, which, not long afterward, appeared in the mathematical nursery rhyme corner of a trade journal. Though the poem is pathetic enough, the real misfortune is that space did not allow acknowledgment to the famous Swiss mathematician, Leonhard Euler. In any event, the episode serves as a prologue to our next endeavor: an examination of several of the important numerical constants of mathematics.
Without question, the most famous of these “numbers” is the one we call π; it has the approximate numerical value π = 3.14159. Although its basic definition relates the circumference of a circle to its diameter, π appears in a large number of mathematical problems that have nothing whatsoever to do with circles.
Another extremely important number is the one identified as e. Its approximate value is e = 2.71828. It serves as the basis for so-called natural logarithms and also for things like exponential growth in demography, radioactive decay in physics, and bell-shaped curves in probability theory. Another famous number is the one called the golden ratio, ø = 1.61803. This number shows up in the strangest places, including the architecture of the Parthenon in Greece and the Great Pyramids of Egypt, the geometry of five-pointed stars and logarithmic spirals, and the shape of sunflower blossoms and Nautilus sea shells.
Yet another important number is Euler's constant. Its numerical value is γ = 0.57721. Again, this number appears in many problems of mathematics including the theory of heat conduction and the theory of extreme value distribution in statistics. Our fifth and final number is also the newest one: the Feigenbaum number, δ = 4.6692. This numerical constant makes its appearance in the relatively new area of mathematics called chaos theory.
In addition to these mathematical constants, there are also a great many physical constants; more than thirty of them are listed by Abramowitz and Stegun (1965). The ones we use in our various analyses are the following:
Gravitational acceleration, g = 9.82 m/s2 (in fact, g changes slightly with latitude, varying from 9.78 at the equator to 9.83 m/s2 at the poles)
Gas constant, R* = 8.314 joule/°K mol
Gravitational constant, G = 6.673 × 10-11 newton m2/kg2
Speed of light, c = 2.998 × 108 m/s
The Most Famous Number of All: π
The most ancient, most familiar, and most important number in all of mathematics—indeed in all of human civilization—is the one we designate with the symbol π. It represents the ratio of the circumference of a circle and its diameter and has the approximate value π = 3.14159. Thus, if C and D are, respectively, the circumference and diameter of a circle, then C = πD. Also, if A is the area of a circle and R = D/2 is its radius, then A = πR2.
More than 4,000 years ago, the Babylonians had established an approximate value for this important number: π = 25/8 (that is, 3.125). At about the same time, the Egyptians had determined that π = 256/81 (3.1605). The greatest mathematician of antiquity, Archimedes of Syracuse (287-212 B.C.), knew that π was more than 223/71 (3.14085) but less than 22/7 (3.14286).
Surprisingly accurate numerical values of π were also known in ancient Chinese, Hindu, and Mayan civilizations. The Bible, however, missed it by quite a bit. A verse in the Old Testament, 1 Kings 7:23, implies the value π = 3. Now perhaps that was an excusable mistake but the following one was not. In 1897, a bill was introduced in the Indiana state legislature which required that π = 3. The bill passed the House of Representatives by a 63 to 0 vote. Fortunately, a mathematics professor from Purdue University arrived on the scene in the nick of time. Thanks to his intervention, the π = 3 bill was withdrawn from deliberation by the Indiana Senate and, to date, has not been considered further.
It turns out that π is an irrational number, that is, it cannot be expressed as a ratio of two integers, like 22/7. In addition, it is a transcendental number, which means that it is not the root of an algebraic equation with integer coefficients, such as x2 – 7x + 12 = 0. The consequence of this transcendental property of π is that the numbers to the right of the decimal point (i.e., 3.14159…) go on forever and ever without any apparent order or pattern.
It has long been a kind of contest or competitive game among mathematicians—and now computer specialists—to enlarge the number of decimal places of π. In the year 1560, it had been established that π = 3.141592, that is, it was known to an accuracy of six numbers to the right of the decimal point. By the end of the sixteenth century, π had been calculated to thirty decimal places. A summary of the growth of our knowledge of the number of known decimal places of π prior to the twentieth century is presented in table 7.1.
TABLE 7.1

With the invention and very fast development of electronic computers during the twentieth century, the number of known decimal places of π has increased rapidly and enormously. In 1947, π was known to 808 places. By 1957, the number had increased to over 10,000 and by 1967 to 500,000. Twenty years later, in 1987, the number had grown to 25 million. In 1997, Professor Kanada and his colleagues at the University of Tokyo computed π to an incredible 51.5 billion decimal places.
One wonders why they want to have all this information about the number of known decimal places of π. Well, for mathematicians involved in number theory, the extensive list of decimal places provides very useful information concerning patterns, distributions, randomness, and other properties and features of number sequences.
Over the years, many analytical methods and mathematical equations have been developed and utilized to calculate π. For example, in the past the following expression has been employed to determine the value of π:
![]()
This kind of equation is called an infinite series. Another well-known expression utilized for the computation of π is
![]()
You might want to try calculating π from equations (7.1) and (7.2). You will quickly discover that they are very slow in producing an answer. Indeed, a good many terms must be employed to obtain even a rough estimate of π. An equation that is much more suitable is the one employed by the noted German mathematician Carl Friedrich Gauss (1777-1855):
![]()
With regard to the use of infinite series for calculating the value of π, a remarkable advance was made in 1995 when the following expression was given by Bailey et al. (1997):
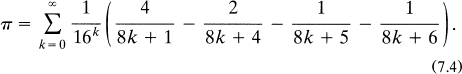
Although this equation is only slightly more complicated than the preceding expressions, it yields the value of π much more quickly. You might want to convince yourself that π is correctly computed to six decimal places by using simply the terms corresponding to k = 0,1,2,3 in equation (7.4).
A charming little book by Beckmann (1977) gives a brief history of π and descriptions of numerous interesting things about it. In addition, the book contains various mnemonic devices for π. As we know, such devices help us remember things. For example, the mnemonic BASMOQ PN3T2 gives the provinces and territories of Canada. There are a great many mnemonics for π. The following one helps us remember its numerical value to fourteen decimal places. The number of letters in each word gives the respective number in the sequence (i.e., 3.14159 26535 8979).
How I want a drink, alcoholic of course, after the heavy lectures involving quantum mechanics.
If you prefer a shorter mnemonic device for π, here is one that will give you seven decimal places (3.1415926):
May I have a large container of coffee?
A substantial contribution was made to mathematics literature with the publication of Pi: A Source Book by Berggren, Borwein, and Borwein (1997). This voluminous work presents the history of this important number over the past 4,000 years. Included in its contents are seventy representative documents on the subject. Most of the contents, of course, deal seriously with the mathematical and computational aspects. For example, the contributions of the Indian mathematical genius Srinivasa Ramanujan (1887-1920) are included in the book.
A good many of the documents in the work deal with strictly historical studies. Thus, considerable attention is given to studies carried out long ago in Egypt, Greece, India, China, and medieval Islam. And finally, a number of presentations are somewhat whimsical or even amusing selections. These include a 402-word mnemonic for π, constructed in the format of a circle, and a display of the numerous documents presented to the Indiana legislature in 1897 to decree the legal value of π.
The Second Most Famous Number: e
Although nearly everyone knows about the number π, its nearest rival in fame and importance, the number e, is virtually unknown outside of mathematics, science, and engineering. The main reason for this is that e, which has the approximate value e = 2.71828, is not really encountered or utilized—except in natural logarithms—until we get involved in calculus and other areas of more advanced mathematics. In these subjects, e is an extremely important numerical constant.
The Swiss mathematician Leonhard Euler (1707-1783) was one of the most prolific in all of history. Among a great many other major contributions, he was the one who assigned the symbol e to this famous number and proved the relationship

This expression says that as the whole number n increases in magnitude, the value of the quantity in parentheses—call it S if you like—approaches the number e = 2.81828. For example, if n = 10, then S = 2.59374; if n = 100, S = 2.70481; if n = 1,000, S = 2.71692; and so on to n = ∞.
Another great mathematician, England's Isaac Newton (1643-1727), showed that
![]()
This expression is another example of an infinite series. From either equation (7.5) or equation (7.6), we can easily compute the value of e. As is true of π, the quantity e is an irrational and also transcendental number.
The topic of logarithms was mentioned above. You probably remember logarithms from your course in elementary algebra though you may not recall that you probably dealt only with so-called “common” logarithms. This is the system in which the number 10 is used as the base of the logarithm—probably because humans have always had 10 fingers.
Now any number can serve as the base of an arithmetic system including operations involving logarithms. In information theory and computer science, the number 2 (“binary”) is generally used although sometimes the numbers 8 (“octal”) and 16 (“hexadecimal”) are employed. In contrast to the use of the number 10 as the base for “common” logarithms, the number e is used as the base for so-called “natural” logarithms. Fine. But why is such a strange number used for this purpose?
A complete answer to this question involves the limiting value property of e expressed by equation (7.5). To be brief, it is simply pointed out that if we use the numerical value e = 2.71828…, then the calculus operations called differentiation and integration are greatly simplified.
For example, suppose we have the simple equation y = cx, where c is a positive constant. If we set c = e, then clearly y = ex. This is called the exponential function. Here comes the calculus. The derivative of this equation is dy/dx = ex. In other words, the derivative of the exponential function is equal to the function itself. By the same token, the integral of ex takes on the same form, that is, ∫ydx = ex. Thus, by using this particular numerical value for e, the function ex, its derivative, and its integral are all equal. For calculus operations, this represents an enormous simplification.
Furthermore, with y = ex, then taking logarithms, we have x = loge y, where the subscript e means that the base of the logarithm is e. This is a “natural” logarithm. Incidentally, loge y is sometimes written In y to avoid confusion with log10 y, the so-called common logarithm. Your calculator probably has keys for both types of logarithms.
An Example: Earning Interest on Your Savings Account
We take a quick look at a topic in which all of us are interested: how much money can you earn on your savings account? To answer the question, we utilize equation (7.5) but change it slightly to the form
![]()
in which P0 = $1,000 is the amount of money you have in your savings account at the beginning of the year, that is, the original principal; r = 6% = 0.06 is the annual interest rate paid by your bank; n is the number of “compounding periods” during the year; and P is the amount of money in your account at the end of the year, i.e., 12 months later. The difference between P and Po is the amount of interest you earned during the year.
Now if the bank compounds your interest earnings only once a year, then n = 1. Accordingly, from equation (7.7), at the end of the year you will have P = $1,000(1 + 0.06/1)1 = $1,060. This is called simple interest. Alternatively, suppose the bank compounds semiannually. In this case, n = 2 and equation (7.7) becomes P = $1,000(1 + 0.06/2)2 = $1,060.90. Next, assume that the bank compounds quarterly. Therefore, n = 4; substituting into equation (7.7) gives P = $1,000(1 + 0.06/4)4 = $1,061.36, and so on. The results of our calculations are listed in table 7.2.
TABLE 7.2

Observation number 1: Suppose that your bank advertises and applies “daily compounding” of interest on your savings account. Then, after 12 months, according to the table, your principal is $1,061.83 and you have earned P – Po = $61.83. Dividing this by the original principal and converting to a percentage gives r* = 6.183%. This is called the yield.
Observation number 2: If there is instantaneous compounding, equation (7.7) becomes P = Poer, which gives P = $1,061.84. Clearly, as far as your interest earning is concerned, it makes essentially no difference whether your bank compounds your savings account daily, hourly, or instantaneously.
Another Example: Geometrical Interpretation of the Number e
Everyone knows that π has a very simple geometrical interpretation. It gives the circumference of a circle in terms of its diameter, C = πD. Alternatively, it expresses the area of a circle in terms of its radius, A = πR2. SO a logical question to ask is, what is the simplest geometrical interpretation you can devise involving that other very important number, e?
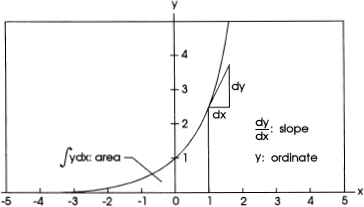
FIG. 7.1
A plot of the exponential function showing the geometrical interpretations of the ordinate, slope, and area under the curve.
To get things started, here is one idea. As we know, the equation of the exponential function is y = ex; this expression is displayed graphically in figure 7.1. Now since y = ex, when x = 1, y = e. So, as shown in figure 7.1, e is the value of the ordinate, y, when the abscissa, x = 1. Further, as pointed out earlier, if y = ex, then the first derivative is dy/dx = ex. It turns out that the first derivative of a function represents the slope of the function. Accordingly, at x = 1, dy/dx = e is the slope of the curve, as shown in the figure. Well, here are two (not terribly exciting) geometrical interpretations of e: the ordinate and the slope of the exponential function at x = 1.
Going further, if y = ex then an integration gives the result ∫ydx = ex if the lower limit of the integral is x = – ∞. The geometrical interpretation of this result is that the total area under the curve between x = – ∞ and x = x is A = ex. If we again select x = 1, then A = e is the area under the curve between x = –∞ and x = 1. This is another geometrical interpretation of e.
You can do much better than this and here is your chance to prove it.
ANNOUNCEMENT OF A GREAT CONTEST INVOLVING THE NUMBER e
Part 1. Devise some kind of relationship that gives a simple geometrical interpretation of e.
Part 2. Manufacture a mnemonic device for e along the lines given earlier for π. For your information, e = 2.71828 18284 59045.
An interesting reference, somewhat analogous to the one by Beckmann (1971) concerning π, is the book by Maor (1994), which deals with our other famous number, e.
Three Other Famous Numbers
We have taken quick looks at the two most famous numbers in mathematics: π and e. There are numerous others; if you are interested in delving further into the matter, a good place to start is the little book by Wells (1986). For the present, we mention three other important numbers.
Golden Ratio, ø = 1.61803
This number defines the ratio of the length L and width H of a rectangle that allegedly gives the most esthetically attractive appearance. Its precise value is L/H = ![]() . We examine this number in detail in chapter 9, “Great Number Sequences: Prime, Fibonacci, and Hailstone.”
. We examine this number in detail in chapter 9, “Great Number Sequences: Prime, Fibonacci, and Hailstone.”
Euler's Constant, γ = 0.57721
This important number, devised by Leonhard Euler around 1750, is defined by the equation γ = (1 + 1/2 + 1/3 +…+ 1/n – loge n) as n becomes infinite. It makes its appearance in many problems in mathematics and statistics.
Feigenbaum Number, δ = 4.66920
This is the newest of the important numbers. It was discovered in 1978 by the American mathematician Mitchell Feigenbaum, in his early studies of chaos theory. This number, δ, is the ratio of the spacings of successive intervals of period doubling in a process leading to chaos. An easily understood description of the nature of δ is presented by Addison (1997).
Some References for More Information
In this brief look at some of the famous numbers of mathematics, we have run across the names of Archimedes, Euler, Gauss, and Newton. These are probably the four greatest mathematicians of all time. If you would like to learn more about them, you will find the book by Muir (1996) to be helpful. It presents interesting biographies of these four notable mathematicians and quite a few others. In addition, the comprehensive work of Boyer (1991) presents a great deal of information about the matter.
Annual Celebration Days for π and Perhaps e
In the preceding sections, we have examined two famous numbers, π and e, and looked briefly at three others, ø, γ, and δ. Noteworthy is the fact that of these five important numbers, only π can be expressed as a date if we require that three significant figures be utilized. That is, π = 3.14 which, of course, is March 14.
It is fitting, therefore, that this most important number of all should be celebrated each year. Accordingly, shall we declare March 14 to be π-Day? If this meets with success, we could, later on, celebrate e-Day on February 7 and perhaps ø-Day on January 6. Suggested first steps: Contact the White House and the greeting card manufacturers.
