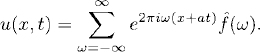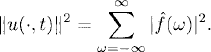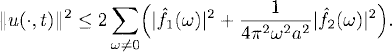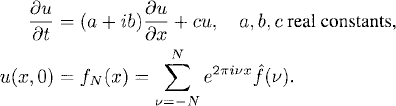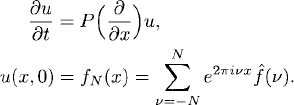CHAPTER 8

1-PERIODIC SOLUTIONS OF TIME DEPENDENT PARTIAL DIFFERENTIAL EQUATIONS WITH CONSTANT COEFFICIENTS

We start this chapter by studying three simple examples of partial differential equations and their initial value problems in the 1-periodic case. These examples are fundamental as model equations and to introduce the concepts of well posedness and stability under lower-order perturbations. At the end we generalize these concepts to more general equations and systems of equations.

8.1 Examples of equations with simple wave solutions

8.1.1 One-way wave equation

Perhaps the simplest example is the one-way wave equation

(8.1)

with initial data:

(8.2)

We solve the problem by separation of variables; that is, we assume that

(8.3)

By (8.2),

Introducing (8.3) into (8.1) gives us

(8.4)

Therefore,

and by (8.3),

(8.5)

We can now use the results of Section 7.2 and the principle of superposition to solve (8.1) for general initial data

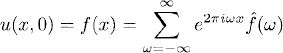
and obtain

(8.6)

By Parseval’s relation we obtain the energy estimate¹

(8.7)

8.1.2 Heat equation

Consider now the heat equation

(8.8)

with initial data (8.2). Again we solve the problem by the separation of variables (8.3) and now obtain

(8.9)

Instead of (8.5), we now obtain

(8.10)

There is a fundamental difference between the behavior of (8.5) and (8.10). For the one-way wave equation, the amplitude of the solution does not change with time. For the heat equation, the amplitude decays rapidly with time if ω is large.

Again, by Section 7.2 and the principle of superposition, we can solve (8.1) for general initial data

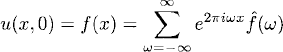
and obtain

(8.11)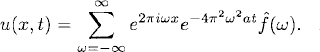

For general initial data, the solution (8.6) has, for t > 0, the same smoothness properties as those of the initial data. For the heat equation, it is C^∞-smooth for t > 0. Therefore, it is much easier to solve (8.8) than (8.1) numerically.

Finally, corresponding to (8.7), we obtain for the heat equation an energy estimate

(8.12)

8.1.3 Wave equation

Consider finally the wave equation,

(8.13)

For constant initial data the solution is simply u(x, t) = σ₁ + σ₂t. For nonconstant initial data we start by studying simple wave solutions. We again make the ansatz (8.3)

and obtain a second-order ordinary differential equation

(8.14)

Its general solution is of the form

(8.15)

We need two initial conditions,

(8.16)

Thus,

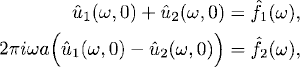
and

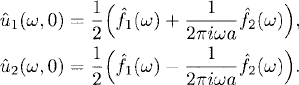
Thus,

(8.17)

Equation (8.17) consists of two solutions of type (8.6). We can again use the results of Section 7.2 and the principle of superposition to solve (8.13) for the general data

(8.18)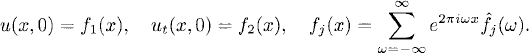

Then the general solution is

(8.19)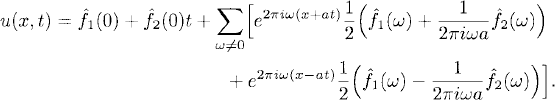

Again we obtain an energy estimate that, for vanishing ₁ (0) and ₂(0), is

(8.20)

Exercise 8.1 Derive estimate (8.20).

8.2 Discussion of well posed problems for time dependent partial differential equations with constant coefficients and with 1-periodic boundary conditions

8.2.1 First-order equations

We start with

(8.21)

Because (8.21) is of the same type as the first example of Section 8.1, we could proceed as before, using the ansatz (8.3). However, we shall Fourier transform the problem directly. Since the Fourier transform of f_N(x) consists of a finite number of frequencies, we know that the solution of (8.21) exists and is C^∞-smooth. We obtain

Integration by parts with respect to x, and taking the time derivative outside the integral, gives us

(8.22)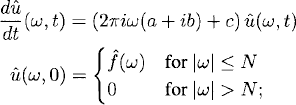

that is, for |ω| ≤ N,

(8.23)

The corresponding simple wave solution is given by

(8.24)

that is,

(8.25)

Inverting the Fourier series, we obtain

(8.26)

and by Parseval’s relation we obtain the energy estimate

(8.27)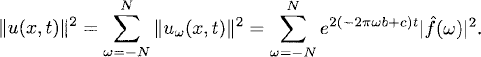

Using the ansatz (8.3), we would have obtained the same result.

For every fixed N there is a bounded solution. However, even if ω is of moderate size, the corresponding simple wave solution can grow rapidly with time. For example, if ωb = −10, t = 10, c = 0, then

In numerical calculations, due to truncation errors, all frequencies are activated, that is |ω| → ∞. Therefore, we cannot calculate the solutions if ωb < 0, and we call the problem illposed.

On the other hand, if b = 0, then

If c > 0, there is exponential growth but it does not depend on ω. This is quite common in applications and we have to live with it. In this case we call the problem well posed. The most benign situation occurs when c ≤ 0 because there is no growth at all (see the first example in Section 8.1); we call the problem strongly well posed.

8.2.2 Second-order (in space) equations

Now we add a second-order term to (8.21) and consider

(8.28)

As before, we Fourier transform (8.28) and obtain

(8.29)

Therefore, for |ω| ≤ N,

that is,

(8.30)

The behavior of the simple wave solution is determined by d.

1. If d < 0, for large ω,

Therefore, the exponential growth rate in (8.30) is unbounded for large |ω| and the problem is not well posed. In this case the differential equation (8.28) is called the backward heat equation.

2. If d > 0, for sufficiently large |ω| the exponent in (8.30) becomes negative:

Even when e(ω) may be positive for some frequencies—for example, if 0 < d 1, we have e(ω) ≤ E, E independent of ω. There may be exponential growth for low frequencies, but this growth cannot become arbitrarily large; that is,

In this case the problem is well posed.

8.2.3 General equation

We summarize our results. Consider

(8.31)

Here

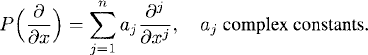
We solve the problem by Fourier transform. Since

we obtain

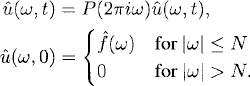
Here is called the symbol of the differential operator P(∂/∂x). The corresponding simple wave solution is given by

Therefore,

By the superposition principle, the general solution of problem (8.31) is given by (8.26). The well posedness of the problem is characterized in terms of the symbol in the following theorem.

Theorem 8.1 Problem (8.21) is ill posed if there is a sequence ω_j such that

It is well posed if there is a constant K such that for all ω,

It is strongly well posed if K ≤ 0.

8.2.4 Stability against lower-order terms and systems of equations

We consider problem (8.31) and assume that a_n ≠ 0. Then we call a_n∂ⁿ/∂xⁿ the principal part of the differential operator P(∂/∂x), and the other terms, lower-order terms. By Theorem 8.1 it is clear that for our model problems (8.21) and (8.28), the lower-order terms have no influence as to whether the problems are well posed.

To generalize this result to hyperbolic and parabolic systems of equations we will use energy estimates. Before considering systems we want to show how to get energy estimates for the one-way wave and the heat equations without using the Fourier representation. We construct energy estimates in the physical space by applying integration by parts, a powerful technique that can also be applied to nonperiodic problems.

One-way wave equation. We again consider equation (8.1) with initial data u(x, 0) = f(x), with f a smooth 1-periodic function. The energy is defined as

(8.32)

The energy is conserved in this problem. Integration by parts gives us

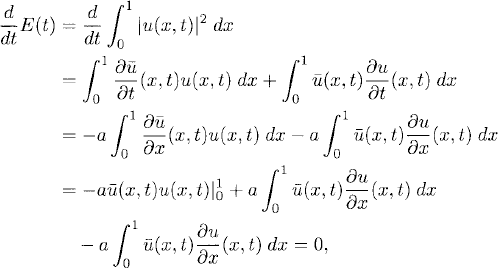
where the first term vanished because of the periodicity. Therefore, by integrating in time we get

(8.33)

which is equivalent to (8.7).

Heat equation. Now consider equation (8.8) with initial data u(x, 0) = f(x), smooth, and 1-periodic. The energy is again defined by (8.32) and decays for this problem.

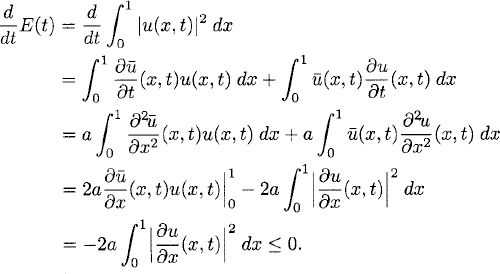
The energy strictly decays until the solution becomes constant. In general,

(8.34)

Systems of equations. We now generalize the result of the preceding section to 1-periodic hyperbolic and parabolic systems in one space dimension. We consider the hyperbolic system

(8.35)

Here u = (u₁, u₂, …, u_n)^T is a vector-valued function with complex components and A, B are constant n x n matrices with A real, nonsingular, and symmetric.

We also consider a parabolic system of the form

(8.36)

where D is symmetric and positive definite. To begin with, we neglect lower-order terms and consider

(8.37)

Since A, D are symmetric, there are unitary matrices U₁ and U₂ which transform, respectively, A and D to diagonal form. Therefore, we make the change of variables u = U₁, u = U₂, respectively, and obtain

(8.38)

Here λ_j, j = 1,2, are real diagonal matrices and λ₂ is positive definite. Thus, we have reduced our problems to scalar equations, and the initial value problems are well posed.

Systems (8.35) and (8.36) can, in general, not be reduced to diagonal form. Therefore, we use integration by parts.

The L₂-norm for a vector-valued function u is

Here | | is the Euclidean norm introduced in Chapter 6.

For (8.35),

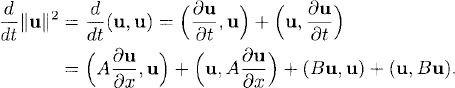
Since

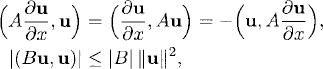
where we use the induced matrix norm (see Definition 6.1), we obtain

and, integrating, the energy estimate follows for system (8.35).

For (8.36),

(8.39)

Observing that D is positive definite, integration by parts gives us

(8.40)

Here δ is the smallest eigenvalue of D. Also,

(8.41)

Using (8.40) and (8.41) in (8.39), we obtain

(8.42)

Integrating, we get the energy estimate for (8.36).

Exercise 8.2 Show (8.42).

As with scalar equations, the lower-order terms have no influence on whether the problem is well. However, they have do have an influence on whether the problem is strongly well posed.

A very general theory for systems of differential equations in any number of space dimensions has been developed in [[7], Chapter 2]. From the point of view of well posedness, for parabolic systems, symmetric hyperbolic systems, and mixed hyperbolic-parabolic systems, the lower-order terms can be neglected.

¹ It is usual, in the context of PDE theory, to call energy the L₂-norm (or some other Sobolev norm) of the solution. This energy is not necessarily related to physical energy.