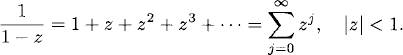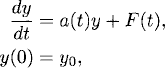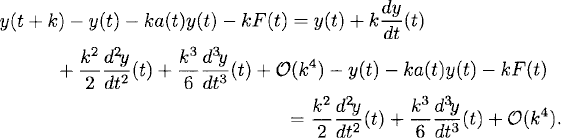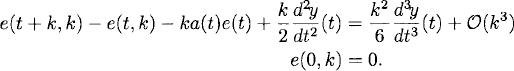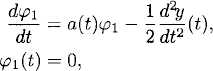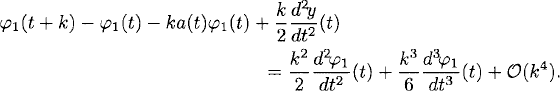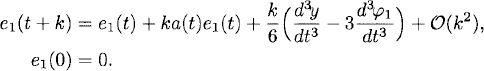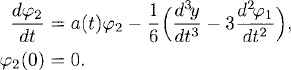APPENDIX A
AUXILIARY MATERIAL
A.1 Some useful Taylor series
We collect here some useful Taylor series used throughout the text, z denotes a complex variable, and the expression on the right denotes the convergence region.
(A.1) 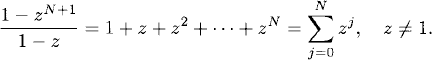
(A.3) 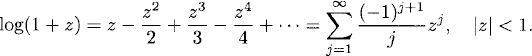
A.2 “ ” notation
” notation
Definition A.1 Let F(x) be a real function. We say that “F(x) is of order f(x) as x tends to a” and write F(x) = ![]() f(x)) as x → a, if and only if there exist two constants C > 0 and δ > 0 such that |F(x)| ≤ C |f(x)| when |x − a| < δ.
f(x)) as x → a, if and only if there exist two constants C > 0 and δ > 0 such that |F(x)| ≤ C |f(x)| when |x − a| < δ.
For example, if F(x) is n + 1 times differentiable around x = a, then by Taylor’s theorem,
![]()
where the remainder term satisfies Rn(x) = ![]() ((x − a)n+1). Here, and many times when it is clear by context, we omit “as x → a.”
((x − a)n+1). Here, and many times when it is clear by context, we omit “as x → a.”
A.3 Solution expansion
In this section we give a derivation of the solution expansion: a fundamental expansion in powers of k that relates the numerical approximation to the exact solution of an initial value problem. We derive this expansion for the particular case of the explicit Euler method applied to a linear equation; we then generalize the result, without proof, to other methods.
Consider the scalar initial value problem
where a(t) and F(t) are smooth functions of t.1 By the existence and uniqueness theorem for ordinary differential equations, this problem has a unique smooth solution y(t).
Now, approximate (A.4) by the explicit Euler method:
Here a(t) and F(t) are smooth functions and so is the exact solution y(t). We want to derive an asymptotic expansion, in the variable k, of the error of the approximation v(t, k) − y(t). Use of the notation v(t, k) instead of our usual notation v(t) is to emphasize the dependence of the approximation on the step size k.
The explicit Euler approximation (A.5) is globally accurate of order ![]() (k); therefore, we write v(t, k) = y(t) +
(k); therefore, we write v(t, k) = y(t) + ![]() (k) within the time interval of interest. To make explicit the form of the
(k) within the time interval of interest. To make explicit the form of the ![]() (k) term, we proceed as follows. Substituting the solution y(t) of the differential equation into the difference approximation and using Taylor expansion gives us k times the truncation error,
(k) term, we proceed as follows. Substituting the solution y(t) of the differential equation into the difference approximation and using Taylor expansion gives us k times the truncation error,
We subtract equation (A.6) from (A.5) and obtain for the divided error, e(t, k) = (v(t, k) − y(t))/k,
Here we think d2y/dt2 and d3y/dt3 as given functions. To first order in k [i.e., neglecting ![]() (k2) terms], (A.7) is simply the explicit Euler method applied to the initial value problem
(k2) terms], (A.7) is simply the explicit Euler method applied to the initial value problem
which, as y(t) is smooth, has a unique, smooth exact solution φ1(t). We emphasize here that neither the initial value problem (A.8) nor its solution φ1(t) depend on k. Now, as (A.7) is a difference approximation of (A.8) which is globally accurate of order ![]() (k), we write its solution e(t, k) as e(t, k) = φ1(t) +
(k), we write its solution e(t, k) as e(t, k) = φ1(t) + ![]() (k). That is, the zero-order term in the asymptotic expansion of e(t, k) is φ1(t). To make explicit the
(k). That is, the zero-order term in the asymptotic expansion of e(t, k) is φ1(t). To make explicit the ![]() (k) term in the expansion of e(t, k), we repeat the process. By Taylor expansion and using (A.8), we have
(k) term in the expansion of e(t, k), we repeat the process. By Taylor expansion and using (A.8), we have
Subtracting (A.9) from (A.7) gives us for the divided error e1(t) = (e(t) − φ1(t))/k,
As before, to first order in k, (A.10) is the explicit Euler approximation of the problem
As y(t) and φ1(t) are smooth, the problem (A.11) has a unique solution φ2(t) which is independent of k. Now, as (A.10) is a difference approximation of (A.11), which is globally accurate of order ![]() (k), we write its solution e(t, k) as e(t, k) = φ1(t) +
(k), we write its solution e(t, k) as e(t, k) = φ1(t) + ![]() (k). In this way we get
(k). In this way we get
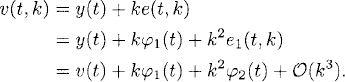
Of course, one could expand the truncation error (A.6) to higher order in k. In that case we could also repeat the process above to higher order. To summarize, by the procedure above one can show the following representation of the solution v(t, k) of the explicit Euler approximation to the initial value problem (A.4).
Theorem A.2 Given any positive integer N, the solution v(t, k) of (A.2) can be written as
(A.12) ![]()
Here the functions φj(t) are solutions of linear inhomogeneous differential equations, which do not depend on k.
By the procedure used above, we can prove a result valid for a general one-step approximation to an initial value problem. Consider an initial value problem
where f(y, t) is assumed to be a smooth function; thus, there exists a unique exact solution y(t) and a T > 0 such that y(t) is smooth for t ![]() [0, T].
[0, T].
We approximate (A.13) by a one-step numerical method
locally accurate of order ![]() (kp+1). As before, we write v(t, k) to emphasize the dependence of v on the step size k.
(kp+1). As before, we write v(t, k) to emphasize the dependence of v on the step size k.
We state without proof the following result.
Theorem A.3 Given a positive integer N, there exists a positive constant KN and a positive time TN ≤ T such that the solution v(k, t) of (A.14) admits the expansion
(A.15) ![]()
for k ≤ KN and t ![]() [0, TN]. Here the functions φj(t) are solutions of nonlinear equations that do not depend on k.
[0, TN]. Here the functions φj(t) are solutions of nonlinear equations that do not depend on k.
1 Throughout this appendix, “smooth” means C∞-smooth. This smoothness condition can be relaxed depending on how large the order is that one wants to make explicit in the expansion, but we do not go into the details here.