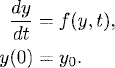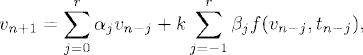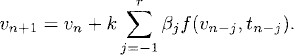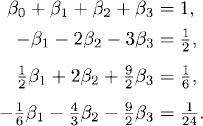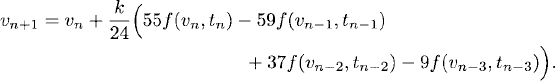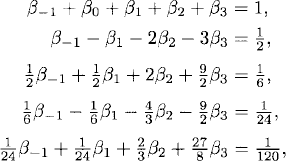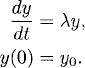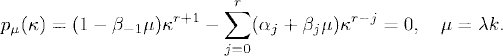CHAPTER 5

TWO-STEP AND MULTISTEP METHODS

The character of some equations, such as the equations of motion in a many-body problem in Newtonian mechanics, requires methods of high and very high orders of accuracy. The use of high-order one-step methods (such as Runge-Kutta methods) for such problems turns out to be computationally very expensive. For this reason multistep methods have been developed. These methods can be both of very high accuracy and fast. In this chapter we study the leapfrog method, which is the simplest of all, and Adams methods, which include both explicit and implicit methods. At the end we show a simple example of the predictor-corrector strategy for multistep methods.

5.1 Multistep methods

Consider the initial value problem

(5.1)

Thus far, we have approximated equation (5.1) by one-step methods (see Definition 2.9). They have the form

(5.2)

If we know v_n, we can calculate v_n+1. Another class of methods are the multistep methods.¹

Definition 5.1 A multistep method to approximate equation (5.1) is of the form

(5.3)

where α_j and β_j are given constants and r ≥ 1. The method is said to be explicit if β₋₁ = 0 and implicit otherwise.

The constants α_j and β_j, which determine a particular method, are chosen to have good accuracy and stability properties.

Notice that to apply a multistep method to the initial value problem (5.1) we set v₀ = y₀ and then need to prescribe the first r steps v₁, v₂, …, v_r by some supplementary rule, since the iteration needs the previous r + 1 values of v_j. This is a drawback of multistep methods compared to one-step methods if during calculation one has to change the step size to maintain the accuracy. In the latter all that is necessary to start the iteration is the initial condition v₀ = y₀.

Multistep methods are, however, preferred in applications where a very high degree of accuracy is necessary, such as for orbit calculation in many-body problems. The reason is the following. A one-step method would require several evaluations of the function f(v, t) at every time step (e.g., Runge-Kutta methods) or, even worse, evaluations of the function and some of its derivatives (e.g., Taylor methods). On the other hand, a multistep method would require only one evaluation of the function f(v, t) at every time step, because it reuses the evaluations performed in the preceding r + 1 steps. In many applications the evaluation of f(v, t) is by far the most expensive part of the computation; then multistep methods are more efficient.

5.2 Leapfrog method

In this section we consider one particular method, the leapfrog method, which is given by

(5.4)

This method is the explicit two-step method that follows, with r = 1, from (5.3) with α₀ = 0, α₁ = 1, β₋₁ = 0, β₀ = 2, and β₁ = 0, that is, it can be written

(5.5)

It turns out that this method is very efficient for oscillator problems, such as

(5.6)

and also for systems of equations arising from hyperbolic partial differential equations.

The leapfrog method is an example of a two-step method: To compute v_n+1, one needs the previous two values, v_n and v_n-1. In particular, to start the computations one needs v₀ and v₁. Clearly, if an initial value condition y(0) = y₀ is given for (5.2), one can choose v₀ = y₀. To get v₁ one can use the explicit Euler method, for example. Then the starting data for (5.5) are

(5.7)

Exercise 5.1 Why is (5.5), (5.7) second-order accurate?

Truncation error. We will now calculate the truncation error R_n of the leapfrog method. By definition, r_n is obtained if one substitutes the exact solution y(t) into the difference equations (5.4). Note that

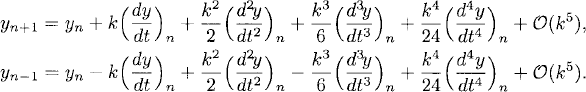
Therefore,

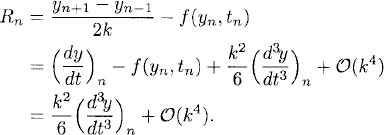
That is, to leading order the truncation error is .

Stability. To calculate the stability of the leapfrog method, we apply it to the model equation,

The leapfrog approximation is

(5.8)

Clearly, the solution of (5.8) is determined uniquely by an initial condition

(5.9)

Generalizing Definition 3.6, we define the stability region as follows.

Definition 5.2 The stability region of the leapfrog method consists of all complex numbers λk for which all solutions of (5.8), (5.9) are uniformly bounded for all n = 0, 1, 2, 3, ….

Solutions of difference equations. We first try to find a solution of (5.8) which is of the form

(5.10)

Introducing (5.10) into (5.8) gives us

Thus, (5.10) is a solution if and only if κ satisfies the so-called characteristic equation

(5.11)

Clearly,

are solutions of (5.11). Concerning the difference equation (5.5) with initial conditions (5.9), we have to distinguish between two cases.

Stability region. Since we have computed the general solution of the difference equation (5.8), we can now determine the stability region of the leapfrog method.

Theorem 5.3 The stability region of the leapfrog method consists of all λk with

Proof: First note that the two points λk = ±i do not belong to the stability region because, by (5.15), the solution of (5.8) is generally unbounded. Now, let λk = ai, a , |a| < 1. The roots of the characteristic equation (5.11) are

with |κ_j|² = a² + (1 − a²) = 1. It follows that all solutions of (5.12) remain bounded and the method is stable.

Conversely, assume that λk belongs to the stability region. For the roots κ_1,2 of the characteristic equation we have

Since |κ₁| ≤ 1 and |κ₂| ≤ 1 we find that |κ₁| = |κ₂|⁻¹ and then |κ₁| = |κ₂| = 1. Thus,

Therefore,

and the assertion λk = ia, a , |a| < 1 follows.

Modified leapfrog method. Since the stability region for the leapfrog method lies on the imaginary axis, one can expect the method to work well for oscillatory problems such as (5.6). For other problems we have to modify it. Consider, for example,

(5.16)

One can approximate (5.16) by

which is equivalent to

(5.17)

The modified method is second-order accurate.

Exercise 5.2 Prove that the stability region of the modified leapfrog method (5.16) includes the semiunit disk x² + y² < 1, x ≤ 0.

5.3 Adams methods

Definition 5.4 The Adams methods are multistep methods with α₀ = 1 and α_j = 0 for j = 1, 2, 3, …, r. They are of the form

(5.18)

The constants β_j are chosen to get the accuracy and stability properties desired. For example, the Adams-Bashforth are explicit Adams methods; that is, they choose β₋₁ = 0, and β_j with j = 0, 1, …, r so that the accuracy order of the method is as high as possible. It can be shown that an equivalent way to obtain the coefficients is as follows. Integrating equation (5.1) between t_n and t_n+1 gives

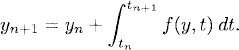
If we replace f(y, t) in the integral by its interpolating polynomial of degree r, at the grid points t_n, t_n-1, t_n-2, …, t_n-r, replace y by v as usual, and integrate, we get the Adams-Bashforth method.

Exercise 5.3 Show that the one-step Adams-Bashforth method is just the explicit Euler method and derive the two-step Adams-Bashforth method. Hint: Instead of using the general equation (5.1), use the linear equation dy/dt = λy.

We derive as an example the four-step Adams-Bashforth method, (i.e. with r = 3). It is enough to consider the linear equation dy/dt = λy. Inserting the exact solution into (5.18) and using Taylor expansions centered in y_n we see that we can cancel the first four terms of the local error expansion if the following equations are satisfied

(5.19)

These equations have the unique solution β₀ = 55/24, β₁ = −59/24, β₂ = 37/24, and β₃ = −3/8, which gives the fourth-order accurate method

(5.20)

In general, the β_j, j = 0, 1, …, r, coefficients in a (r + 1)-step Adams-Bashforth method can be chosen to cancel terms in the local error expansion up to (k^r+1). The resulting method is accurate of order r + 1.

If one chooses β₋₁ ≠ 0 in (5.18), on obtains implicit methods called Adams-Moulton methods. In this case one has r + 2 constants to determine and one further term of the local error expansion can be canceled (compared to the Adams-Bashforth methods), thus obtaining an (r + 2)-order accurate method. For example, with a fourth-step Adams-Moulton method we can cancel the first five terms in the local error expansion. The system of equations to satisfy is

(5.21)

whose unique solution is β₋₁ = 251/720, β₀ = 323/360, β₁ = −11/30, β₂ = 53/360, and β₃ = −19/720. The method is fifth-order accurate, given by

(5.22)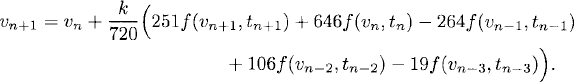

Exercise 5.4 Derive the systems of equations (5.19) and (5.21).

Initial steps. To apply a multistep method one needs to obtain the first r − 1 steps with a different method. A possibility is to use a one-step method of the same order. For example, to apply (5.20), one could compute v₁, v₂, and v₃, applying three steps of the classical fourth-order Runge-Kutta method (3.5).

5.4 Stability of multistep methods

Consider the model problem

(5.23)

Definition 5.5 Multistep method (5.3) is said to be stable if when applied to problem (5.4), the solution v_n stays bounded for all n = 0, 1, 2, ….

One can proceed as in the leapfrog method to find solutions of the multistep method. One first looks for solutions of the form v_n = κⁿ. Plugging v_n into the difference equations (5.3) for the particular problem (5.23) gives

(5.24)

This polynomial equation of degree r + 1 in κ, whose coefficients are linear functions of μ, is sometimes called a characteristic equation. When p_μ(κ) has r + 1 distinct roots κ_j, j = 1, 2, …, r + 1, the general solution of the multi-step method can be written as

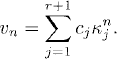
In this case the method is clearly stable when |κ_j| ≤ 1, j = 1, 2, …, r + 1. When some of the roots κ_j are multiple roots (i.e., have multiplicity greater than 1), some other independent solutions of the form

are needed to expand the general solution v_n. The general solution will be bounded provided that these multiple roots of (5.24) satisfy |κ_j| < 1. Then we have

Lemma 5.6 The multistep method (5.3) is stable if the solutions κ_j of (5.24) satisfy

(5.25)

The stability region of the multistep method consists of all the μ in the complex plane such that the method is stable. The fact that all the coefficients of P_μ(κ) are linear functions of μ allows one to apply a simple procedure, known as the boundary locus method, to find the stability region. To understand this method, notice first that p_μ(κ) = 0 can be written as

(5.26)

where

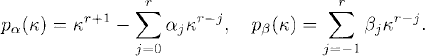
By continuity, because of (5.25), for every μ on the boundary of the stability region, at least one of the eigenvalues κ_j satisfies |κ_j| = 1. Writing this eigenvalue as κ = e^iθ and using (5.26), we have, for the μ on the boundary,

(5.27)

Therefore, to find the boundary of the stability region, one can plot the curve (5.27) for θ [0, 2π]. This is clearly a closed curve that splits the complex μ-plane in two or more domains. Then, by computing all the roots of p_μ(κ) in one arbitrary interior point on every domain to check the condition (5.25), one can identify which of these domains belong to the stability region and which of them do not. Consider, for example, the four-step Adams-Bashforth method (5.20); we have

The curve (5.27) divides the complex plane into four domains (see Figure 5.1).

Figure 5.1 Boundary locus for the four-step Adams-Bashforth method.

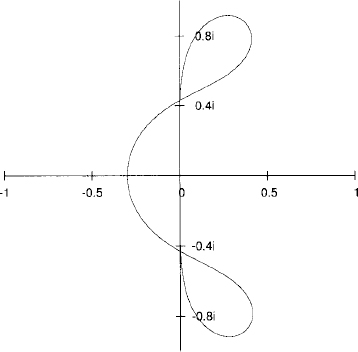
Exercise 5.5 Show that the only domain of Figure 5.1 belonging to the stability region of the four-step Adams-Bashforth method is the one just left of the origin.

Predictor-corrector strategy. In many applications it might be interesting to use implicit multistep methods such as the Adams-Moulton methods introduced earlier. However, the implicit character of these methods implies that one needs to solve large systems of algebraic equations, which become complicated or computationally expensive. A procedure designed to overcome this difficulty is to use an implicit method in combination with an explicit method as a predictor. Here we simply give an example that uses a third-order Adams-Bashforth method as a predictor and a fourth-order Adams-Moulton method as a corrector. If one wants to solve the equation

this predictor-corrector scheme is

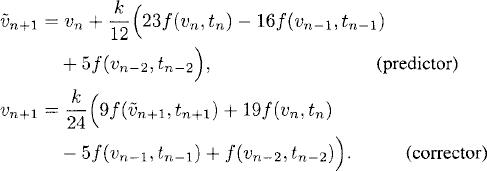
The resulting scheme is clearly explicit.

¹Methods of the form (5.3) are sometimes called linear multistep methods, because they use only linear combinations of the values v_j and f(v_j, t_j).