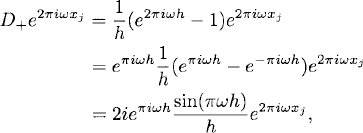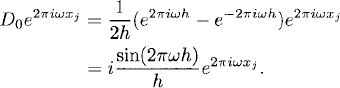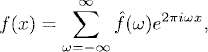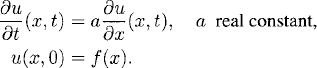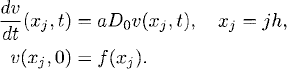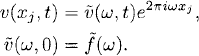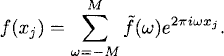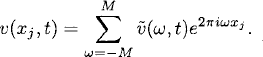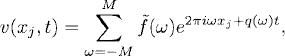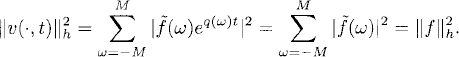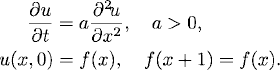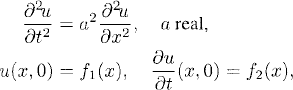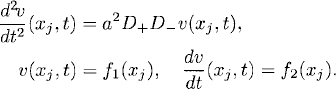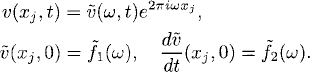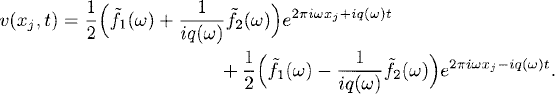CHAPTER 9

APPROXIMATIONS OF 1-PERIODIC SOLUTIONS OF PARTIAL DIFFERENTIAL EQUATIONS

In this chapter we introduce basic finite difference operators that approximate space derivatives and spectral derivatives that are based on Fourier theory. Then the method of lines, a very useful approach that consists of approximating the space derivatives but keeping the time continuous, is explained. Under this approach the partial differential equations become systems of ordinary differential equations, and therefore we can use the results of the first part of the book to analyze the model problems.

9.1 Approximations of space derivatives

Let M be a positive integer and h = (2M + 1)⁻¹ a grid size. The corresponding grid points are denoted by x_j = jh, j = 0, ±1, ±2, …. A grid function f_j = f(x_j) is simply a function defined on the grid. It is called 1-periodic if

and therefore any 1-periodic grid function is well defined by its 2M + 1 values f₀, f₁, …, f_2M.

The most common difference operators approximating d/dx are D₊, D₋, D₀, which are defined by

(9.1)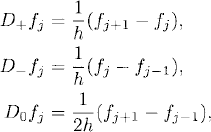

and which are called forward, backward, and centered difference operators, respectively. Clearly, if f_j is 1-periodic, then D₊f_j, D₋f_j, and D₀f_j are also 1-periodic.

Discretization error and order of accuracy. Let f_j denote the restriction of a smooth function f(x) to the grid. The discretization error is the deviation from the exact derivative of the function at a grid point when this derivative is approximated by a difference operator. As the truncation error of a difference approximation to an ordinary differential equation, it can be computed by Taylor expansion. For example, we have

A similar expansion holds for f_j-1. These expansions give

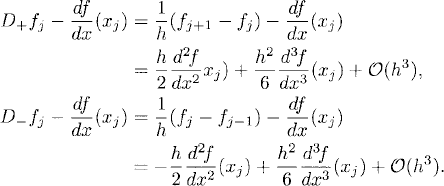
This equations mean that D₊ and D₋ are first-order accurate approximations of the first derivative of f. Because

we obtain from the error expansions above,

(9.2)

that is, D₀ is a second-order accurate approximation of d/dx.

The difference operator D₀ uses the values of the grid function at three consecutive points to compute the derivative at the center point; one says that D₀ has a span of three points. One can, of course, write difference operators that use more than three points to construct difference operators with a higher order of accuracy.

Exercise 9.1 Deduce a five-point span centered difference approximation to the first derivative which is accurate of order 4.

Application to Exponentials. Because we intend to use Fourier interpolation, it is important to understand the action of the difference operators on the exponential grid functions e^2πiωx_j, Because of

we obtain

(9.3)

(9.4)

(9.5)

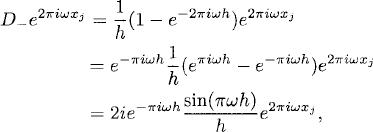
We note that the factor multiplying the grid function e^2πiωx_j on the right-hand sides is always independent of j. Therefore, the grid function e^2πiωx_j is an eigenfunction of each of the operators D₊, D₋, D₀. Upon application of any of these operators, the exponential goes over into a multiple of itself.

For fixed x_j and j → 0, the left-hand sides of the formula above converge to (d/dx)e^2πiωx|_x=xj. This follows from the above consideration of the discretization error. Also, if we expand the sine function about zero, we see that the right-hand sides converge to 2πiωx_j. Of course, the limits of the two sides are equal since

(9.6)

Remark 9.1 Equation (9.6) says that e^2πiωx is an eigenvector of the operator d/dx with eigenvalue 2πiω. If one replaces d/dx by D₊ or D₋ or D₀, one obtains the eigenrelations (9.3)–(9.5). A remarkable fact is that only the eigenvalue gets perturbed by this replacement whereas the eigenfunction of each of the discrete operators is precisely the restriction of e^2πiωx to the grid. We will see below why this is important for stability analysis.

Approximation for d²/dx². A very commonly used difference approximation for the second derivative is given by D₊D₋; this is

By Taylor expansion,

(9.7)

which shows that D₊D₋ is a second-order accurate approximation of d²/dx². Also, from the expression above for D₊ and D₋ applied to e^2πiωx_j, we obtain

(9.8)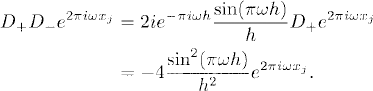

Exercise 9.2 Find α such that the difference operator

is a fourth-order accurate approximation of d² f(x_j)/dx². What is the span of this operator?

9.1.1 Smoothness of the Fourier interpolant

Here we state and prove an important property of the Fourier interpolant introduced in Section 7.3.

Let f(x) be a 1-periodic function and f^I(x) be its Fourier interpolant on a given grid x_j = hj, j = 0, ±1, ±2, …, where h = 1/(2M + 1) is the mesh size, that is,

(9.9)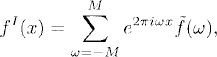

where the Fourier interpolant coefficients (ω) are computed as in (7.13).

Theorem 9.2

(9.10)

We emphasize that the constant (π/2)^p does not depend on the mesh size h.

Proof: We differentiate f^I(x) p times and use the orthogonality of the exponentials (7.2) to get

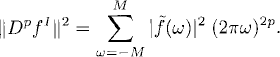
Applying D₊ p times to f(x) at the grid point x_j we get, by (9.3),

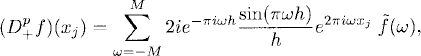
so that, by (7.16),

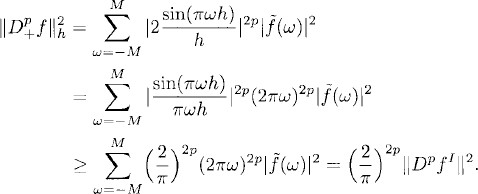
9.2 Differentiation of Periodic Functions

If we have a 1-periodic smooth function f(x) we have a Fourier series representation

(9.11)

and we know that the derivative of f(x) can be obtained by multiplying every Fourier coefficient in (9.11) by 2πiω.

Now, assume that we know the restriction of this smooth function to a grid x_j [i.e., we know the grid function f_j = f(x_j)]. How can we efficiently compute a good approximation to the derivative df/dx at the grid points x_j?

A good answer is: We first use FFT to calculate the coefficients (ω) of the Fourier interpolant

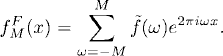
We know that f_j = f^I (x_j). Then we differentiate f_M^F (x) exactly and evaluate on the grid:

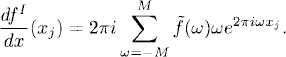
The values of df^I(x_j)/dx are good approximations of df(x_j)/dx and can be computed efficiently by applying IFFT to the coefficients 2πiωf(ω).

9.3 Method of lines

The so called method of lines consists of approximating the space derivatives of a partial differential equation (e.g., by difference approximations) while keeping the time continuous. This semidiscrete approach is very useful to a study of the stability of difference methods of solving the equation. In the method of lines the partial differential equation becomes a system of ordinary differential equations, as we will see. In practice, the method of lines also makes reference to a way of writing computer codes to solve partial differential equations such that the numerical method used to integrate in time can easily be changed without changing the approximation of the space derivatives. In this section we introduce the method of lines by applying it to the model equations of Chapter 8.

9.3.1 One-way wave equation

Consider the initial value problem

(9.12)

We assume that f(x) and therefore also u(x, t) are smooth functions which are 1-periodic in x. We shall only discretize the space dimension but keep the time continuous. Let M be a positive integer, h = (2M + 1)⁻¹ a mesh size thaht defines the grid points x_j, j = 0, ±1, ±2, …. We approximate (9.12) on the grid by

(9.13)

We are interested in solutions that are 1-periodic on the grid [i.e., v(x_j+2M+1, t) = v(x_j, t)], so that (9.13) is a system of 2M + 1 coupled differential equations. The easiest way to calculate the solution is to use essentially the same procedure as that used in Chapter 8.

We start with simple wave solutions and use separation of variables, that is, given a frequency ω, we make the ansatz

(9.14)

By Section 9.1, introducing (9.14) into (9.13) gives us

(9.15)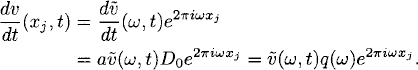

Here q(ω) = ai(sin(2πωh)/h) is called the amplification factor. Therefore,

(9.16)

that is,

(9.17)

By (9.14) and (9.17),

(9.18)

which is a second-order accurate approximation of u(x_j, t) on the grid when the initial data function is is purely imaginary, then and the approximation is stable.

It is important to notice that every mode (i.e. the solution for a fixed frequency ω), satisfies an ordinary differential equation. By (9.13)–(9.18),

(9.19)

One can compare (9.18) with the exact solution (8.5). For low modes (i.e., |ωh| 1), q(ω) ≃ 2πiωa, and the solution behaves like the exact solution. For high modes, , and q(ω) ≃ 0, the amplitude is preserved, but the phase error becomes large.

As our problem is linear, we can now use the results of Section 7.3 and the principle of superposition to solve (9.12) for general initial data. Consider the semi-discretized problem (9.13) with general 1-periodic initial data. The initial data function can be Fourier interpolated on the grid as in (7.11):

(9.20)

Also, the solution can be Fourier interpolated:

(9.21)

By orthogonality of the exponentials [see (7.12)], . Inserting (9.21) into (9.13) gives, again by orthogonality of the exponentials, exactly the problem (9.16) for each individual frequency ω. By (9.21) the general solution is a superposition of solutions (9.18),

(9.22)

which is a second-order accurate approximation of u(x_j, t) on the grid. By the discrete Parseval’s relation (7.16), and because q(ω) is purely imaginary,

(9.23)

By (9.23) the energy is preserved during time evolution by the semi-discretized equation (i.e., the approximation is stable).

We now consider the one-way wave equation (9.12) with a lower-order term,

(9.24)

which we approximate on the grid by

Then the amplification factor becomes

Thus,

and v(x, t) behaves like the solutions in Chapter 8.

Artificial dissipation. The addition of a dissipative term to the discrete scheme (9.13) can be used to minimize the bad effect of inaccurately computed high-frequency modes. Instead of (9.13), consider the approximation

(9.25)

which is consistent with (9.24) since the added term is proportional to a second derivative multiplied by h, and thus it vanishes formally when h → 0. The amplification factor becomes

(9.26)

For small |ωh| we obtain in first approximation

If ω²h → 0, then q → a2πiω and v(x, t) behaves like the solution of the well-posed problem [see (8.4].

If ω²h 1 (i.e., we consider high frequencies), Re q → ∞ if b < 0 and ω²h → ∞ and the approximation is unstable. If b > 0, Re q → −∞ for high frequencies and the approximation is stable.

In applications, high frequencies (i.e., if ω ≥ 1/h) are not calculated with any accuracy; the artificial dissipation term hbD₊D_−v, b > 0, helps to control these inaccurate high-frequency terms. Unfortunately, the approximation becomes only first-order accurate because the low frequencies are also affected. To prevent loss of accuracy, the standard artificial dissipation term is the fourth order term,

Now the approximation is second-order accurate.

Exercise 9.3 Prove that the approximation

to (9.24) is second-order accurate.

The purpose of the method of lines is to have a way to sort out the methods thaht are definitely unstable. For equations with variable coefficients, one uses the principle of frozen coefficients. For example, if in (9.12) a = a(x, t) is a smooth function, one replaces a(x, t) by a(x₀, t₀) and treats the constant coefficient problem. If, for any (x₀, t₀), the method is unstable, the method has to be improved. General theory tells us that if the method is stable at (x, t) = (x₀, t₀), it must be stable in the neighborhood of that point. If a method is stable at all relevant values of (x, t), it can be applied to the variable coefficient problem.

9.3.2 Heat equation

Consider the 1-periodic initial value problem for the heat equation as in Chapter 8:

(9.27)

On the same grid as for the one-way wave equation, we approximate (9.27) by

(9.28)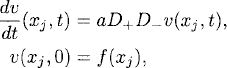

and look for 1-periodic solutions on the grid. With the simple wave ansatz (9.14), we again obtain

(9.29)

where the amplification factor is now

(9.30)

This is as in the previous case a second-order accurate approximation of u(x_j, t) on the grid when the initial data function is .

All the approximate modes (9.29) with ω ≠ 0 are decaying exponentially with time, so that the approximation is stable. Notice that small,

and the solution is dominated by the exact solution (8.10). When |ωh| ~ 1/2, the approximation is not accurate, but this is not important, as both the exact and approximate modes decay, for any t > 0, very fast exponentially.

Each individual mode (9.29) satisfies an ordinary equation

(9.31)

In complete analogy with the one-way equation, the solution of (9.27) with general 1-periodic initial data (9.20) is obtained, by superposition of simple wave solutions as in (9.22) but with q(ω) given by (9.30). Using the discrete Parseval’s relation, one can prove that the energy E(t) = ||v(x_j, t)||² decays to ; thus, the approximation is stable.

We consider now the heat equation perturbed with lower-order terms [see eq. (8.28)]. We study the second-order accurate semidiscrete approximation

Fourier transforming, we find that

where the amplification factor is

Thus, when |ωh| is small, q(ω) = −4π²ω²d + 2πω(a + ib) + c, and the solution behaves like the exact solution of Chapter 8.

9.3.3 Wave equation

We consider our third model problem of Chapter 8, the 1-periodic wave equation

(9.32)

with f₁(x + 1) = f₁(x) and f₂(x + 1) = f₂(x). On the same grid as in the previous model problems, we approximate (9.32) by

(9.33)

Again we look for simple wave solutions of the form

(9.34)

Inserting (9.34) into (9.33) gives us

(9.35)

Therefore, calling q(ω) = 2a[sin(πωh)/h], we have

(9.36)

and (9.34) gives

(9.37)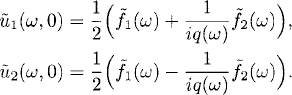

The simple wave solution is then

(9.38)

This solution is a second-order accurate approximation of the exact simple wave solution (8.17). When ωh is small, q(ω) ~ 2aπω and the (9.38) behaves like the exact solution. When |hω| is large, |hω| ~ 1/2, we have q(ω) ~ 4aω compared to the value 2πaω of the exact solution (i.e., the phase error of high modes is large). One can improve the situation by using a higher-order approximation.

9.4 Time Discretizations and Stability Analysis

One-way wave equation. We shall now also discretize time. By (9.19),

(9.39)

Thus, we have, for every grid point x_j, and every frequency ω, an ordinary differential equation which we write in the form

(9.40)

Assume that we want to integrate in time using a time step k, that is, we discretize time as t_n = kn, n = 0, 1, 2, …. We need the chosen method to be stable to integrate all modes. In other words, we need kq(ω) to belong to the stability region of the method for all ω.

For wave propagation problems, the leapfrog method, which we discussed in Chapter 5, is often a very efficient method. Let v_n denote the approximation to y(t_n). Then

(9.41)

As q(ω) is pure imaginary, k > 0 can be chosen small enough so that kq(ω) belongs to the leapfrog’s stability region (see Theorem 5.3). Moreover,

Therefore |q(ω)| < |a|/h, and the condition

(9.42)

implies stability. For condition (9.42), is known as CFL condition,¹ the maximum speed of propagation of the completely discretized scheme (i.e., h/k) needs to be higher or equal to the physical speed |a| of the wave. CFL conditions frequently appear as stability conditions in wave propagation problems.

If q(ω) has a real part, kq(ω) cannot belong to leapfrog’s stability region. One can use the modified leapfrog method of Chapter 5. Assume that

then the modified leapfrog method is

(9.43)

In Exercise 5.2 we found that this method is stable if kη(ω) ≤ 0 and kξ(ω) < 1.

Exercise 9.4 The approximation (9.25) for the constant coefficient problem (9.12) can be cured to be second-order accurate by tunning the parameter b if one uses explicit Euler to integrate in time. Consider the approximation (9.25) for problem (9.12) and use explicit Euler to integrate in time. Prove that the truncation error

(9.44)

where u(x, t) is the exact solution of(9.12), is

(9.45)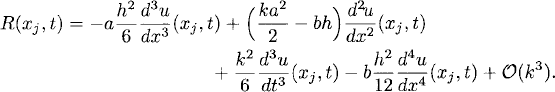

Therefore, if we choose b = a²k/2h, the method becomes second-order accurate in both space and time. The approximation (9.44) is known as the Lax-Wendroff method.

Heat equation. If we discretize time and use, for example, the explicit Euler meth: od to integrate the equation, stability requires that −2 ≤ kq(ω) ≤ 0, as −4a/h² ≤ q(ω)) ≤ 0. Then k is chosen so that

Even when explicit Euler is only first-order accurate, the choice of k proportional to h² gives an approximation that is second-order accurate in the parameter h.

Exercise 9.5 Consider initial value problem (9.27) with a = 1 and

with k = h²/10, where v_jⁿ = v(x_j, t_n) approximates the solution at the grid point x_j = h_j and time t_n = kn. Write a computer program that computes v_jⁿ and show plots of the solution at the same times as those for item (a) using h = 1/10.

at t_n = 0.2 as a function of x_j. Do you get the resulti expected?

Wave equation. Differentiating (9.38) twice, we get for every mode

(9.46)

which has the form of an ordinary differential equation,

(9.47)

Calling vⁿ the approximation of y(t_n), the two-step method

(9.48)

is clearly second-order accurate. We want to study the stability of (9.48). As usual, we assume that vⁿ = κⁿ; then

(9.49)

If −4 < λk² < 0, this equation has two different, complex, unitary roots, thus giving a stable approximation.

Exercise 9.6 Prove the last assertion.

In our application

Without loss of generality we assume that the zero-frequency mode (constant mode) is absent, that is,

(9.50)

Then we have 0 < sin² (πωh) < , and the stability condition is satisfied if the CFL condition (9.42) is satisfied.

We have just shown that the completely discretized centered two-step approximation

(9.51)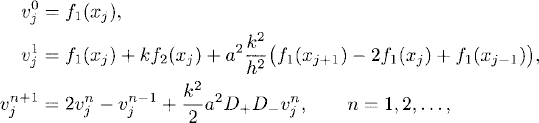

is second-order accurate (in both h and k) and stable if the time step is chosen to satisfy CFL condition (9.42) and (9.50) holds.

¹From Courant-Friedrich-Lewy.