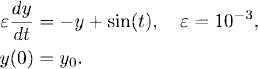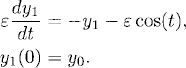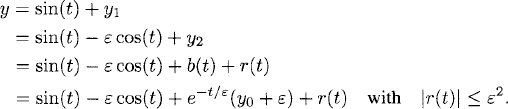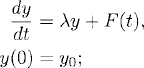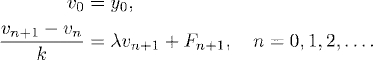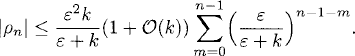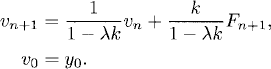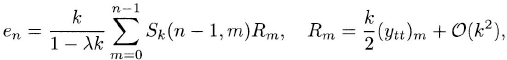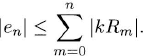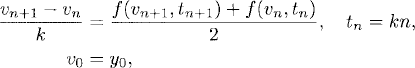CHAPTER 4

IMPLICIT EULER METHOD

Some differential equations, such as stiff equations, are difficult to approximate using explicit methods because the stability condition imposes severe restrictions on the time step. It is therefore very useful to introduce a new class of methods, called implicit methods. In this chapter we explain some basic properties of stiff equations by analyzing a simple model equation. Then we introduce the implicit Euler method, which is the most basic implicit method. At the end of the chapter a very simple variable-step-size strategy is explained. This strategy shows the fundamental idea behind more complex strategies used in higher-order methods.

4.1 Stiff equations

Many applications lead to Stiff differential equations. A simple example of a stiff equation is

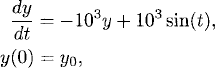
which can also be written as

(4.1)

This equation can be solved exactly using lemma 1.2. The exact solution is

(4.2)

To gain insight into the behavior of the solution, instead of analyzing the exact solution (4.2), we prefer to use a general procedure to obtain the dominant terms of this solution. This procedure has the advantage that it can be applied to more general problems where the exact solutions are not known.

If we formally set ε = 0 in (4.1), we see that the function y = sin(t) satisfies the equation. This motivates us to define a new variable y₁ by

For the function y₁ (t), one obtains

(4.3)

Thus, the forcing in the y₁-equation is reduced to order (ε). We repeat the process and define y₂ by

Then y₂ satisfies

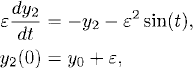
and the forcing is of order (ε²). Clearly, we could continue the process and reduce the forcing to even higher order in ε.

Since the initial data in the y₂-equation are (1), in general, the function y₂ will not be small. Therefore, we now solve

that is,

Then the function r(t) = y₂ (t) − b(t) solves

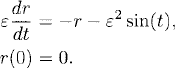
The function r(t) plays the role of a remainder term: The forcing and the initial data in the r-equation are both small, and therefore we can expect r(t) to be small. Indeed, using the explicit formula (1.9), we obtain

and can estimate |r(t)|,

To summarize, the solution y(t) of (4.1) has the following representation:

(4.4)

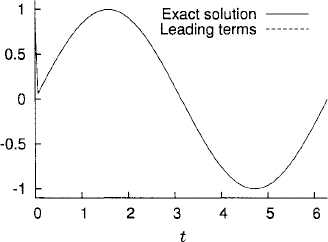
The representation (4.4) provides the leading terms of the asymptotic expansion of the exact solution y(t). It shows that except for a small remainder r(t) = (ε²), the solution of (4.3) consists of a slowly varying part, sin(t) − ε cos(t), and an initial layer, e^−t/ε(y₀ + ε). Figure 4.1 shows a plot of both the exact solution (4.2) and the first three terms of the asymptotic expansion (4.4) [i.e., without the remainder r(t)].

Figure 4.1 The exact solution (4.2) and the leading terms in the asymptotic expansion (4.4) look completely superimposed in this plot.

Suppose that we try to solve (4.1) numerically by the explicit Euler method. To obtain a reasonable approximation, we must choose the step size k so that λk = −k/ε belongs to the stability region of the method (i.e., so that k ≤ 2ε). From an accuracy point of view, such a small step size is adequate in the initial layer, where the solution changes rapidly. Away from the initial layer, one would like to choose a larger step size since the solution varies slowly. With explicit Euler, however, a larger step size cannot be chosen. If k > 2ε, the method becomes unstable, which leads to growing rapid oscillations.

4.2 Implicit Euler method

When approximating the solution of (4.1), the possibility of choosing a small time step to solve the initial layer and a bigger time step for the rest of the solution can be implemented for the implicit Euler method. Assume that we want to approximate

(4.5)

then

Definition 4.1 The implicit Euler method to approximate (4.5) is defined by

(4.6)

For (4.1) the approximation reads

To discuss how the approximation behaves, we derive an asymptotic expansion for v_n = v_n(k,ε) which is similar to the asymptotic expansion of the exact solution y(t) given in (4.4).

First we make a change of variables,

and obtain

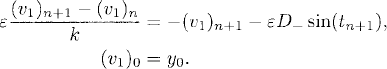
Here we denote by D₋ the difference operator

so that, by Taylor expansion,

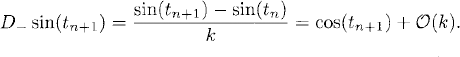
We repeat the process and set

Then (v₂)_n satisfies

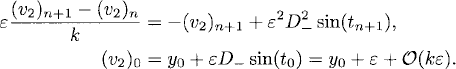
The equation for (v₂)_n can be written as

(4.7)

To obtain the discrete limit layer, we solve the homogeneous equation

that is,

Thus,

where

is the solution operator. Then if we define

ρ_n satisfies the same difference equations as (v₂)_n does, but the initial value is ρ₀ = 0. We can now use the discrete version of Duhamel’s principle. If we identify ρ_n with e_n and the inhomogeneity in (4.7) with kR_n, we can apply Lemma 2.6. We have

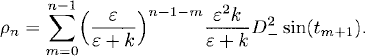
By Taylor expansion

so that

Therefore,

(4.8)

The last factor on the right-hand side is a finite geometric series [see (A.1)], so that

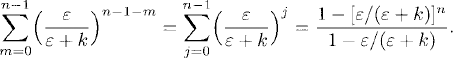
As ε/(ε + k) < 1, from (4.8) we have

Thus, for the complete solution v_n we get

(4.9)

Comparing (4.9) with (4.4), we see that the slowly varying part of v_n agrees with the corresponding part of the exact solution, except for terms of order (ε²). The comparison of the initial layer terms is more subtle. Here we must compare

(4.10)

with the corresponding discrete term

(4.11)

By Taylor expansion

Thus, if k/ε 1, the two terms (4.10) and (4.11) are close for all n = 0,1, …. On the other hand, if k/ε is not small, the two terms (4.10) and (4.11) are not close to each other for small n, and therefore v_n is not a good approximation for y_n in the initial layer. If k/ε is not small but n is large, terms (4.10) and (4.11) are both close to zero. This implies that v_n is a good approximation for y_n outside the initial layer, even if k/ε is not small.

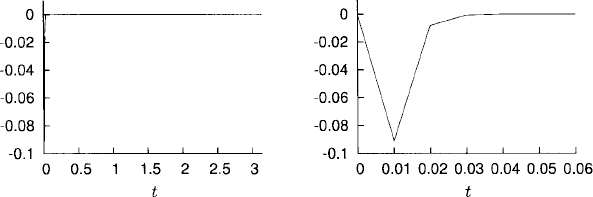
In Figure 4.2 we have plotted the error e_n = y_n − v_n for y₀ = 1, ε = 10⁻³, k = 10⁻². The exact solution was given in (4.2), while v_n was computed numerically. Clearly, k/ε = 10 is not small. Nevertheless, as predicted by our analysis, away from the initial layer the error is small.

Figure 4.2 Error e_n = y_n − v_n in the interval t [0, 2π] (left plot), and of the initial layer, t [0,0.06], (right plot).

We now use the truncation error analysis to discuss the error of the implicit Euler method in the more general case (4.5). We assume that Re λ ≤ 0, with |λ| not large. By definition the truncation error R_n is obtained when we substitute the exact solution y(t) in the difference equations (4.6). By Taylor expansion,

and therefore,

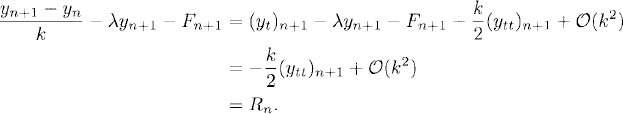
We can write this in the form

(4.12)

Let us note that, to leading order, the truncation errors for the explicit and implicit Euler methods are the same: We have R_n = (k/2)(y_tt)_n + (k²) in both cases. However, the stability region for the two methods is completely different. For the explicit Euler method, as we have seen in Section 2.2, the stability region consisted of all points λk in the complex plane with

that is, the stability region is a disk with radius 1 about the point −1. For the implicit Euler method the amplification factor is (1 − λk)⁻¹, and we have

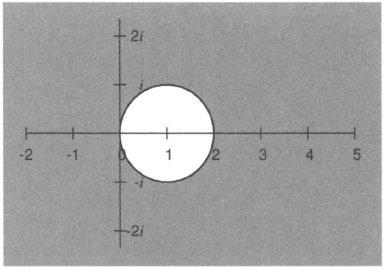
which holds if and only if |1 − λk| ≥ 1; That is, the stability region consists of all points λk in the complex plane outside the disk of radius 1 about point 1 (see Figure 4.3). In particular, all points λk with Re λ < 0 are in the stability region, no matter how large one chooses the step size k. One says that for Re λ < 0, the implicit Euler method is unconditionally stable.

Figure 4.3 The shadowed region is the stability region of the implicit Euler method.

Let us discuss the implications of this good stability property for the error e_n = y_n − v_n. Notice that (4.6) can also be written as

(4.13)

Subtracting (4.13) from (4.12), we obtain

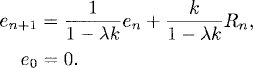
By Lemma 2.6,

(4.14)

where

By assumption we have Re λ < 0, and therefore λk always belongs to the stability region. This yields

and the representation (4.14) implies that

(4.15)

To leading order, kR_m ≃ (k²/2)(y_tt)_m, and therefore (4.15) tells us that we should choose k so that |(k²)(y_t)_m| is small everywhere.

What does this say for our example (4.1)? In the example we have, using (4.4),

(4.16)

The (k²)-term is bounded by Ck² with C independent of ε. In the initial layer, where the term e^−t/ε is (1), we have to choose k so that k ε in order to make (k²/2)|y_tt| small. On the other hand, outside the initial layer, where the term e^−t/ε is small, it suffices to choose k 1. This requirement is then independent of ε. Our analysis suggests that we work with two different step sizes (see Figure 4.4): First we divide the t-axis into two intervals, and . Here

Figure 4.4 Grid with two different step sizes.

is chosen so that ε⁻²e^−t_ε/ε 1. The interval 0 ≤ t ≤ is viewed as the initial layer, because the exponential term ε²e^−t/ε in (4.16) is small for t > . Second, in the interval 0 ≤ t ≤ , we use a step size k with k/ε 1. In the remaining interval, t ≥ , we can work with a step size k satisfying only k 1.

For more complicated problems, which cannot be analyzed as easily, it is a good and common practice to use methods that regulate the step size during computations.

4.3 Simple variable-step-size strategy

Let us describe a simple strategy to construct a variable-step-size implicit Euler method. The idea is to compute, at every time step, an approximation of the leading local error term (k_n²/2)(d²y/dt²)_n (k_n²/2)(d²y/dt²)_n and to regulate the step size so as to keep this term between two given threshold values that we call M and N with 0 < M < N. More precisely, assume that v_n is the computed numerical value at time t_n and k_n is the current step size. Then we compute the preliminary values _n+1/2 and _n+1 by using a step size k_n/2 once and twice respectively. Using these preliminary values, we compute

which is simply an approximation of the leading error term at the intermediate point t_n + k_n/2. Now:

1. If

the error is within the values expected and we accept _n+1 as the value of our numerical approximation at t_n+1 = t_n + k_n and set k_n+1 = k_n.

2. If

our code computed _n+1 with a precision level higher than that requested. We accept _n+1 as the value of our numerical approximation at t_n+1 = t_n + k_n but try the next step with a larger step size by setting k_n+1 = 3/2k_n.

3. If

then the step, and so the error, was too big. We replace k_n by the smaller step size 2/3k_n, and repeat the computation of _n+1/2 and _n+1.

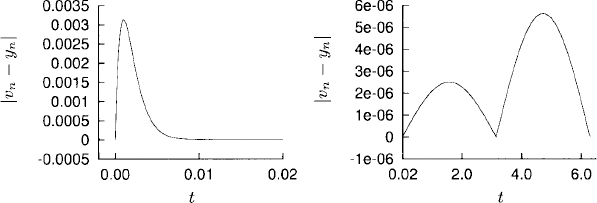
As an example we show the solution to our model problem (4.1) for t [0, 2π], with initial condition y₀ = 1, obtained by applying the implicit Euler method with the variable-step-size strategy just described. The threshold values we use are M = 10⁻⁶ and N = 10⁻³ and an initial time step k₀ = 10⁻². In Figure 4.5 we plot the error |v_n − y_n| of the solution.

Figure 4.5 Error as a function of time. The error in the initial layer is on the left, and the error in the rest of the interval is on the right. Observe the different scales.

Exercise 4.1 Write a code that computes the solution to the example above and

Exercise 4.2 The trapezoidal rule (or method) to approximate the ordinary initial value problem

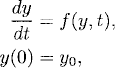
is the implicit method given by:

(4.17)

where, as usual, v_n denotes the approximation to y(t_n).

(a) Show that the stability region is {z , Re z ≤ 0}.

(b) Show that (4.17) is a second-order accurate method.