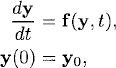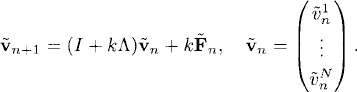CHAPTER 6

SYSTEMS OF DIFFERENTIAL EQUATIONS

In this chapter we motivate, by means of a simple observation, the generalization to systems of equations of what we have learned for scalar differential equations.

Consider the initial value problem for a system of differential equations

(6.1)

where y is an N-component vector and f is an N-component vector-valued function:

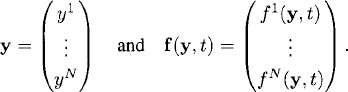
The simplest systems are linear systems with constant coefficients:

(6.2)

Here A is a constant N x N-matrix and F has N components.

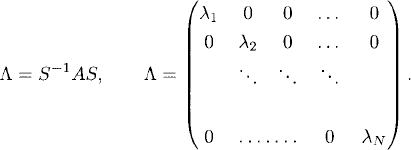
Let us assume that A has a complete set of eigenvectors; that is, there exists a transformation S that transforms A into a diagonal matrix λ:

Exercise 6.1 The exponential of a matrix A ^NxN is defined via the Taylor series,

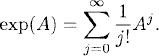
into (6.2), we obtain

(6.3)

with and . Since λ is diagonal, the system above reads in component form

(6.4)

In other words, (6.2) is equivalent to N decoupled scalar equations.

Assume that we approximate every scalar equation in (6.4) with the explicit Euler method on the same grid (i.e., with the same step size k),

These equations read, in vector form,

(6.5)

Then, by using the same transformation S, we have

and (6.5) becomes

(6.6)

which is precisely the definition of the explicit Euler method to approximate the vector system of equations (6.2).

A consequence of these observations is that our analysis of Euler’s method (Chapter 2) for scalar equations carries over to the linear systems described above. The same remark applies to all other methods that we have discussed.

In particular, if Re λ_j < 0 for all j = 0, …, N, we choose the step size k so that kλ_j belongs to the stability region of the method for every j = 1, …, N. Under this restriction, the size of the error e_n = y_n − v_n can be determined by a truncation error analysis similar to the scalar case.

Consider now the nonlinear problem (6.1) and assume that the vector function f is smooth in its arguments. To study how this system behaves, we linearize the problem around the initial data vector given. This is, we write the solution as

and use Taylor expansion for f. We obtain

We assume that the Jacobian matrix of f,

is not singular; then for short times the nonlinear problem is governed by the linear problem

(6.7)

where F(t) = f(y₀, t).

We remind the reader of the definition of a Euclidean vector norm and its subordinate or induced matrix norm:

Definition 6.1 The Euclidean vector norm of u ⁿ is

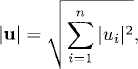
and the “subordinate” or “induced” matrix norm of A ^nxn is

Exercise 6.2 Show that the vector norm and its subordinate matrix norm satisfy

We assume now that the matrix A(t) has a complete system of eigenvectors which are uniformly independent in the time interval of interest, that is, there exists a smooth transformation matrix S(t) such that

and

(6.8)

If Re λ_j(t) < 0, j = 1, 2, …, N, during some time interval 0 ≤ t ≤ T, the solution of (6.1) is driven during some time by N linear, stable, scalar equations. We can integrate numerically in time using any of the methods we studied for scalar ODEs provided that we choose the time step k small enough so that kλ_j(t) belongs in the stability region for j = 1, 2, …, N. From a computational point of view, an implicit assumption is that the norm of the transformation S(t) and that of its inverse are not very large. In other words, the transformation should not be almost singular at any time.

In real computations, it is very important to carry out tests to check whether or not our numerical scheme converges in the time interval of interest. For example, we first compute a solution in a time interval using a time step k. Then we can use half that time step and check that we can compute the solution during the same time interval or at least that the interval of existence of our numerical solution does not go to zero as the time step diminishes. Of course, one can also perform the precision quotient tests of Section 2.6 using any vector norm instead of absolute values.

For completeness we write the explicit Euler method that approximates the general problem (6.1):