Advanced topics

Linear models are the biggest idea in applied statistics and predictive analytics. There are massive volumes written about the smallest details of linear regression. As such, there are some important ideas that we can't go over here because of space concerns, or because it requires knowledge beyond the scope of this book. So you don't feel like you're in the dark, though, here are some of the topics we didn't cover—and that I would have liked to—and why they are neat.

  • Regularization: Regularization was mentioned briefly in the subsection about balancing bias and variance. In this context, regularization is a technique wherein we penalize models for complexity, to varying degrees. My favorite method of regularizing linear models is by using elastic-net regression. It is a fantastic technique and, if you are interested in learning more about it, I suggest you install and read the vignette of the glmnet package:
      > install.packages("glmnet")
  > library(glmnet)
  > vignette("glmnet_beta")
  • Non-linear modeling: Surprisingly, we can model highly non-linear relationships using linear regression. For example, let's say we wanted to build a model that predicts how many raisins to use for a cookie using the cookie's radius as a predictor. The relationship between predictor and target is no longer linear—it's quadratic. However, if we create a new predictor that is the radius squared, the target will now have a linear relationship with the new predictor, and thus, can be captured using linear regression. This basic premise can be extended to capture relationships that are cubic (power of 3), quartic (power of 4), and so on; this is called polynomial regression. Other forms of non-linear modeling don't use polynomial features, but instead, directly fit non-linear functions to the predictors. Among these forms include regression splines and Generalized Additive Models (GAMs).
  • Interaction terms: Just like there are generalizations of linear regression that remove the requirement of linearity, so too are there generalizations of linear regressions that eliminate the need for the strictly additive and independent effects between predictors.

    Take grapefruit juice, for example. Grapefruit juice is well known to block intestinal enzyme CYP3A, and drastically effect how the body absorbs certain medicines. Let's pretend that grapefruit juice was mildly effective at treating existential dysphoria. And suppose there is a drug called Soma that was highly effective at treating this condition. When alleviation of symptoms is plotted as a function of dose, the grapefruit juice will have a very small slope, but the Soma will have a very large slope. Now, if we also pretend that grapefruit juice increases the efficiency of Soma absorption, then the relief of dysphoria of someone taking both grapefruit juice and Soma will be far higher than would be predicted by a multiple regression model that doesn't take into account the synergistic effects of Soma and the juice. The simplest way to model this interaction effect is to include the interaction term in the lm formula, like so:

      > my.model <- lm(relief ~ soma*juice, data=my.data)

    which builds a linear regression formula of the following form:

    Advanced topics

    where if Advanced topics is larger than 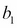Advanced topics and Advanced topics then there is an interaction effect that is being modeled. On the other hand, if Advanced topics is zero and 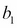Advanced topics and Advanced topics are positive, that suggests that the grapefruit juice completely blocks the effect of Soma (and vice versa).

  • Bayesian linear regression: Bayesian linear regression is an alternative approach to the preceding methods that offers a lot of compelling benefits. One of the major benefits of Bayesian linear regression—which echoes the benefits of Bayesian methods as a whole—is that we obtain a posterior distribution of credible values for each of the beta coefficients. This makes it easy to make probabilistic statements about intervals in which the population coefficient is likely to lie. This makes hypothesis testing very easy.

    Another major benefit is that we are no longer held hostage to the assumption that the residuals are normally distributed. If you were the good person you lay claim to being on your online dating profiles, you would have done the exercises at the end of the last chapter. If so, you would have seen how we could use the t-distribution to make our models more robust to the influence of outliers. In Bayesian linear regression, it is easy to use a t-distributed likelihood function to describe the distribution of the residuals. Lastly, by adjusting the priors on the beta coefficients and making them sharply peaked at zero, we achieve a certain amount of shrinkage regularization for free, and build models that are inherently resistant to overfitting.

Advanced topics
Advanced topics
..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.
Reset
18.218.37.5